年轻的数学家们所需要学习的最重要的东西当然是数学。然而，学习从其他数学家那里得来的经验也是非常有价值的。《给年轻数学家的忠告》一文的五位作者被要求按照他们自己研究数学的经验，对新手给出忠告，就好像他们正在开始自己的学术生涯时所愿意收到的忠告一样。由此写出的经验不仅如我们所期待的那样很有意思，而且更使我们感到惊奇的是它们很少有重复。以下就是这五位数学家写的宝贵经验，虽然它们是针对年轻的数学家们而说的，但是肯定会被所有年纪的数学家们所欣赏和阅读。

在这个数据驱动的时代，更深入的统计学学习可以提供更广泛的职业选择。统计学家感兴趣的一个工作领域是制药行业，最近我们有机会对制药行业了解更多。

数学有时候会变得特别复杂，然而幸好不是所有的数学问题都晦涩难懂。 这里介绍5个没人能解决的“简单”数学问题：Collatz 猜想，移动沙发问题，完美立方体问题，内接正方形问题，美好结局问题。

在19世纪，一个被称为“四元数”的数字的发现为数学家提供了一种描述空间中的旋转的方法，从此永远地改变了物理学和数学。

当爱米·诺特（Emmy Noether，1882-1935）出人意料地决定上大学时，德国舆论才刚开始意识到，有些女性也许会从高等教育中受益。在当时允许女性获得正式学位当然有点不切实际，但经过教授同意，她们可以旁听课程。由于诺特的父亲马克思·诺特（Max Noether，1844-1921）是埃尔朗根大学著名的数学教授，教授们都是他们家的朋友，所以她能得到他们的准许。对于二十世纪初的任何年轻女性来说，这都是一个意想不到的方向，也是诺特在成为本世纪伟大数学家的旅程中，第一次克服困难取得的意料之外的成功。

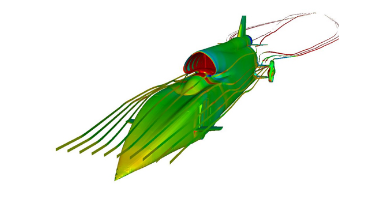
“大部分宇宙充满着类型不一的流体，”对流体动力学有特别兴趣的美国Haverford学院物理教授Jerry Gollub说，“它们的重要性体现在天体物理、工程、医药、健康、化学、地球物理等众多学科里。流体运动构成多尺度意义下的自然现象，具有影响社会的许多应用。”

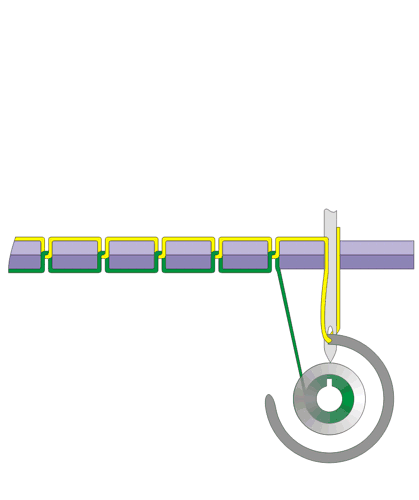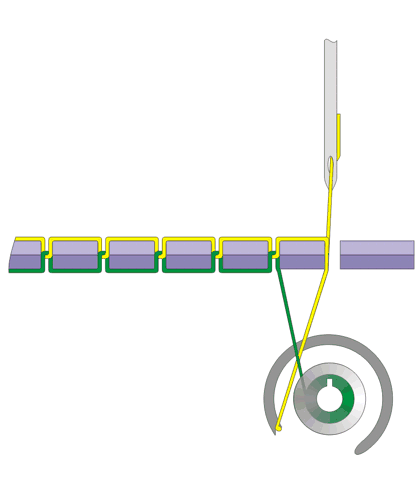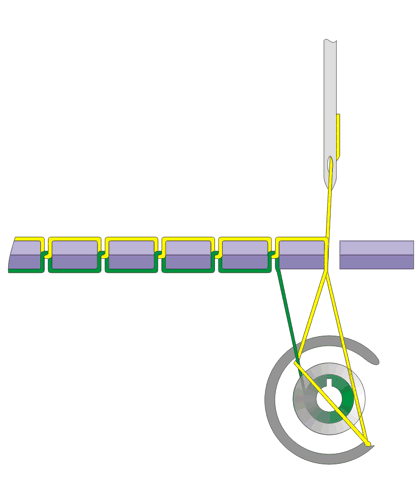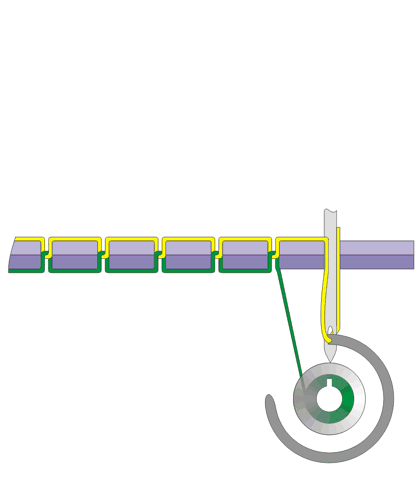
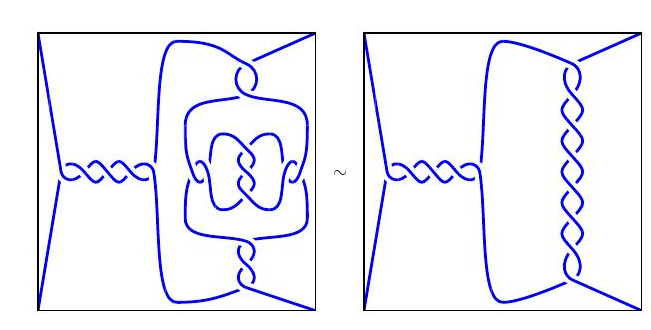
缝纫机是19世纪时人类在机械上的伟大发明之一。（据说，Mahatma Ghandi（圣雄甘地）曾认为它是“为数不多能被称为很有用的发明之一”）与打字机或收音机不同的是，它不能被电子器件替代，因为它处理材料而不是信息。在这个专栏里，我将探究缝纫机与经常和它联系在一起的机器——绕线器——中的数学原理：双线连锁缝纫法在拓朴学上是如何实现的，以及阿基米德螺线形成的凸轮如何保证线均匀缠绕在长线轴上。

在本文中，我们将描述有理缠结和有理数之间的一一对应关系，并看到解有理缠结的过程与欧几里得算法之间的联系。

你会让数学模型决定你的生命吗?如果你还记得2008年的金融危机，那么你的答案很可能是"不"。大多数人将这场金融危机归咎于错误的数学模型预测。

国际数学家大会（ICM）每四年举行一次。这是全世界数学家最大规模的聚会（2014年，第二十七届国际数学家大会在首尔召开，吸引了来自122个国家的5000多名代表参加）这次大会最引人注目的是颁发菲尔兹奖（the Fields medal），它是数学中最重要的奖项之一。然而，尽管聚集在一起的数学家们装作喜欢这些聚会超越了对政治的喜爱，但他们参加这样的聚会总是受到政治事件的影响。