译文
论无穷(2)
《论无穷》一文是希尔伯特在 1925 年 6 月 4 日在 Westphalian Mathematical Society 于 Münster 召开的一次纪念 Karl Weierstrass (魏尔斯特拉斯)的会议上的演说,发表在Mathematische Annalen的 vol. 95 (1926), pp. 161-90 上。
论无穷(1)

《论无穷》一文是希尔伯特在 1925 年 6 月 4 日在 Westphalian Mathematical Society 于 Münster 召开的一次纪念 Karl Weierstrass (魏尔斯特拉斯)的会议上的演说,发表在Mathematische Annalen的 vol. 95 (1926), pp. 161-90 上。
有限群表示一百年

任何一门学科领域里的数学概念的发现和发展常常要经过一段时间,因此通常无法为某个发现指定具体的日期。但是有几个情形,一个发现可能与具有唯一的或具体性质的事件伴随,使得这个发现本身能够与那个事件等同。这方面的一个众所周知的例子是 Hamilton 发现四元数,这总是与他在 1843 年 10 月 16 日沿着都柏林皇家运河的著名的散步联系在一起。
数学作为一门合乎需要的语言

这个会议称为“数学的统一性”。 我想对这个精彩的主题做少许评论。我不认为自己是先知,我只是一个学生。在我的一生中,我曾经师从于像欧拉 (Euler) 和高斯 (Gauss) 那样的伟大数学家、比我年长或年轻的同事、我的朋友和合作者,最重要的是向我的学生学习。这就是我持续工作的方式。
无穷的艺术

无穷一直是绘画、雕塑等视觉艺术形式的主题,亦是诗歌和小说作品的主题。这里讨论了几种结合艺术、科学和数学无穷思想的创作。本文还介绍了作者和他的合作者兰迪・莱茵(Randy Rhine)设计的一种新型的雕塑。
算术-几何均值不等式等价于 Bernoulli 不等式
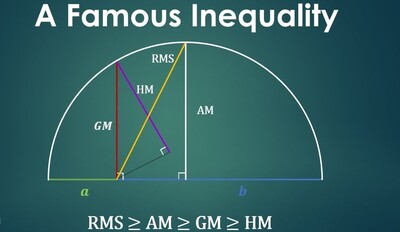
算术-几何平均值不等式有时称为 Cauchy 不等式,对这个不等式 (其中\(n\in \mathbb {N}\) ), 在著作 [1] 与 [2] 中分别给出了 52 种和 74 种证明, 并且数学家仍然在发现新的证明。
辛化、复化与数学三元组
数学中有些部分被认为是独立的部分甚至是不同的数学、比如说实变函数论和复变函数论就被认为是完全不同的学科。莫斯科数学学派的起源正是基于实变数学和复变数学的哲学不同,这是由数学家 Bugaev 发现的。他是已有一百五十年历史的莫斯科数学会的创建者之一,他也是个哲学家和著名的俄罗斯象征主义诗人 Belyi 的父亲。 Bugaev 观察到哲学中有两种主要的思想;命运的思想和自由意志的思想(你能自由运动你的手)他推测命运思想的数学翻版是复变函数论,在那里在一点的芽通过解析延拓已经包括了这个函数的所有信息。
人工智能的机器可能有意识吗?菲尔茨奖得主大卫·芒福德教授撰文探讨

人工智能的列车高速向前,模拟一个人脑、让计算机产生“意识”的可能性似乎比以前大了一点点。意识是什么、机器是否可能拥有意识,也就成了计算机科学家、神经科学家、数学家、哲学家越来越多探讨的课题,其中就包括 1974 年菲尔茨奖得大卫・芒福德(David Mumford)教授。
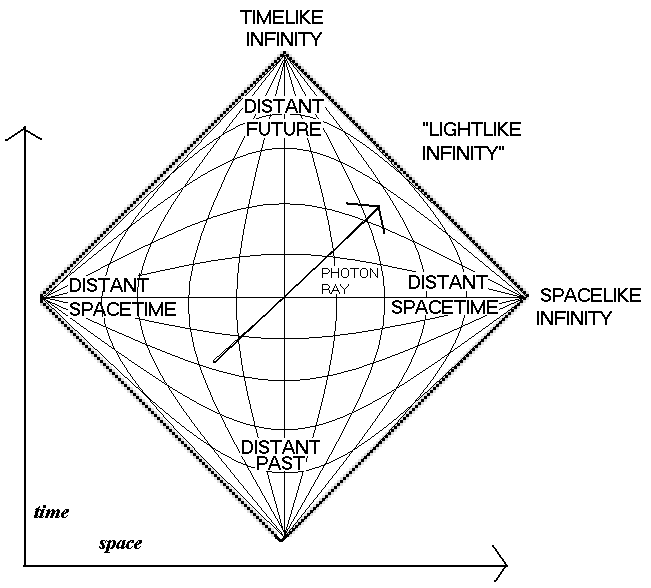
引力与电

狭义相对论导致一个发现,即时间是作为第四个坐标以平等的地位和三个空间坐标连系在一起的,于是物质事件的实况即世界,是一个四维度规连续区。这样一来,确定世界度规性质的二次形式(2),就不必像三维空间几何那样必定是正定二次形式,而是具有惯性指数 3 黎曼本人没有忘记指出,这二次形式应看作一种物理实在,因为它是作为对物质施加实际影响的根源而出现(例如离心力)的,可想而知,物质也会给它以反作用。