这是 V. I. Arnold 于 1997 年 6 月在 Fields 研究所为庆祝其 60 大寿而举行的会议中三份讲稿中的第二份。原题：Symplectization, Complexification and Mathematical Trinities. 译自：预印本。

占卜不是代数。人类不是预盲家而是猜想者。他能观察事物的一般情形并从中提出深刻的猜想。这些猎想经常被时间所证实。

A. S. Pushkin

本讲座的目的是解释一些数学梦想。

数学中有些部分被认为是独立的部分甚至是不同的数学、比如说实变函数论和复变函数论就被认为是完全不同的学科。莫斯科数学学派的起源正是基于实变数学和复变数学的哲学不同，这是由数学家 Bugaev 发现的。他是已有一百五十年历史的莫斯科数学会的创建者之一，他也是个哲学家和著名的俄罗斯象征主义诗人 Belyi 的父亲。 Bugaev 观察到哲学中有两种主要的思想；命运的思想和自由意志的思想（你能自由运动你的手）他推测命运思想的数学翻版是复变函数论，在那里在一点的芽通过解析延拓已经包括了这个函数的所有信息。但是在十九世纪自由的思想更重要，所以 Bugaev 决定在俄国应发展自由意志思想的数学版一实函数论。所以他派他的学主 Egorov 和旨来 Luzin 去巴黎。在那里 Lebesgue 和 Borel 在实变数学上工作。这就是莫斯科数学学派的起源（到很晩以后才统一了实的和复的思想）。

本次讲座我将有意识地用到一些不同数学间的神秘的关系。我将试图解释我在过去使用它们的方式。找希望在将来某个人给它一个理论。我恐怕太老丁没法去形式化所有这些、这里的想法只是些事实，不是理论。对我将描述的我没有公理。我只有例子，但我认为这些例子是自然的，有趣的。为解释这些思想，我从有限维线性代数模型开始，而大多数有兴趣的部分是无限维，在那儿我们在微分几何方面工作，流形代替了向量空间，徽分同胚代替线性变换，等等。

从有限维的情形开始在多伦多这里是非常自然的，因为对数学家来说多伦多同 Coxeter 的名字联系在一起。所以我用 Coxeter 群表开始。这是由欧儿里德反射产生的有限群。它们由 Dykin 图来描述，见图 1 在奇点理论中有 $E$ 的无穷序列，但是在这儿我们将不讨论它们。所以在左边是 $ADE$ 列，在右边的图中含有两条线，也包括（不幸地）最后一个 Weyl 群，它有三条线。

这些群保持某些格因此被称为结晶体群。我们也有非结晶体 Coxeter 群：正 $P$ 边形对称群，正二十面体对称群和超正二十面体对称群 (图 2)。超二十面体正多面体 $H_4$ 存在于 $4$ 维空间。Coxeter 给它一个很好的描述。可能太好了以至没法放进 Bourbaki 的《李群和李代数》，那里描述 $H_3$ 而不是 $H_4$！

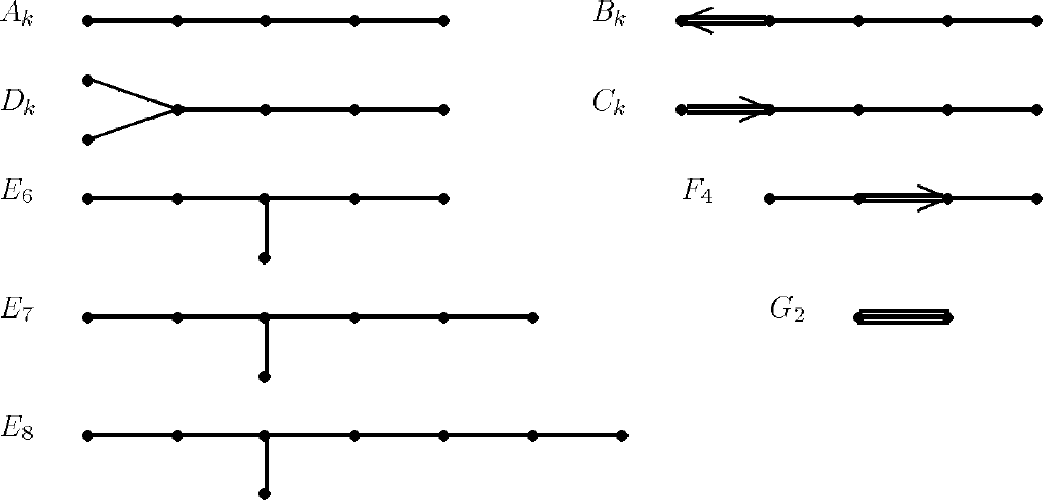图 1：结晶体 Coxeter 群

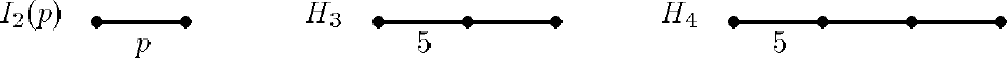图 2：非结晶体 Coxeter 群

图 1，图 2 中每个点表示欧氏空间中一个向量。两个点用单线联结表示两个向量之问角度是 $120^{\circ}$，双线表示角度 $135^{\circ}$，三条线表示角度 $150^{\circ}$ 图 2 的 $p$ 线表示 $180^{\circ}(1-\frac{1}{p})$。因为我们只需方向所以省略了向量长度的描述。我们可以在正交于这些向量的镜面上构造反射。最后产生的群只在某些特殊情况下是有限的。一变换群称为不可约的如果作用空间在由群元所表示的变换下没有非平凡的不变子空间。每个 Coxeter 群可分解成不可约 Coxeter 群的直积，它们作用在相互正交的子空间上，有限维不可约 Coxeter 群所有可能的 Dykin 图都在图 1-2 中。所以这个表给岀了不可约 Coxeter 群的分类, 这是数学中主要的分类定理之一¹。

最简单非平凡 Coxeter 群 $A_2$ 由欧氏平面上两个夹角 $120^{\circ}$ 的单位向量所刻划 (图 3)。全部的镜面是 3 个，而 $A_2$ 由其中任两个生成。所以仏是正三甬形对称群。在一般情况生成反射由图 1-2 中的 Dykin 图描述。例如图 2 中对 $p = 5$ 我们得到正五边形对称群，还有正二十面体和超正二十面体对称群。超正二十面体是由少中 $120$ 个顶点所牛成的凸体，这 $120$ 个点构成了 $S U(2) \simeq S^{3}$ 的一个子群。这个子群在自然的两重覆盖映射 $S^{3} \longrightarrow S O(3)$ 下。是保持正二十面体的 $60$ 个旋转所成群的原像。

群 $A_k$ 也对应于特殊线性群 $SL(k+1)$, 它由行列式为 $1$ 的 $(k+1) \times(k+1)$ 阶矩阵

组成 (或者对应于酉群，如果你喜欢紧的情情形类似地图 1 中左边的所有群在反射下保持某些格不变，它们也被这些 Dykki 图分类，同时它们也对应单李代数。$B_k$ 对应于 $SO(2k+1)$，$C_k$ 对应 $S_p(2k)$，$D_k$ 对应 $SO(2k)$。它们各自有持征值，特征向量和 Jordan 块的理论。例如矩阵的通常谱论是对应于 $A$ 的理论，而 $B$ 和 $D$ 的理论是奇数和偶数维空间的欧氏几何。

图 3：$A_2$ 群的生成元和镜面

Coxeter 群理论把线性代数描成一个更一般理论的持殊情况。你可以避免提到矩阵、特征值和特征向量, 而用 4 系列的根系几何代替任何事情。现在如果你从线性代数或矩阵中取出某些结果并且用根系的语言重新叙述它，那么 (加上概念意义的适当变化）这个结果变成了一个猜想，你可以试图对所有的根系去证明。对图 1 中其他情形证明它可能获得一些有趣的非平凡的结果。

当然你可以认为所有这些结果是线性代数 $(A_k)$ 的持殊情况，也就是说对有附加结构的向量空间的线性代数的研究。例如你可以加上欧氏结构这导致只考虑保持数积的矩阵（$D_k$ 和 $B_k$）或者你可以考虑一个辛 2 次形式使向量空间变成辛空间从而考虑辛线性映射 $(C_k)$ 所以图 1 中的所有理论都可认为是线性代数的子理论。但是有另一种方式去考虑它们。我们可以把它们当做线性代数的姐妹而不是孩子。线性代数只是 Coxeter 群中之一的 $A$ 系列的理论。我们也可以研究其它 Coxeter 群如 $B$，$C$，$D$ 系列的理论一所以我们可以对不同系列构造相类似的定理，而且通过进一步的工作可能会对例外群发现它们的翻版。

现在考虑无限维情况。分类定理推广了图 1 的分类要归于 E. Cartan。对应于 $A_k$ 的第一个情形是流形 $M$ 的微分同胚群 $\mathrm{Diff}(M)$ 对应的李代数由向量场连同标准对易关系组成，这样获得的几何被称为微分几何。有 6 个基本序列它们与徴分同胚群的关系就如同图 1 中第一个 Coxeter 群 $A_k$ 与其它序列的关系。所以有很多其它的几何。第一个是微分亢何。其次我们有流体动力学。它对应于保体积微分同胚群 $\mathrm{SDiff}(M,v)$ 假设流形竝装配了体积元 $v$ 它的李代数由无散向量场 (divergence-free) 组成。然后我们有辛几何。它的群是辛同胚群 $\mathrm{Symp}(M,\omega)$ 它的李代数由局部 Hamilton 向量场组成。还有其它几何：复的，接触的等等。当然所有这些几何的群是第一个的子群，但是它们不是正规子群因为 $\mathrm{Diff}(M)$ 的单位分支是单的。

现在我们把姐妹的概念推广到我们的情形，把这些无穷维群考虑成姐妹。我们从微分几何和拓扑中一些概念，思想和定理开始，然后把它们翻译成类似于根系的语言。之后通过逆过程我们试图去理解在辛情况下或复情况下或其它情况下它们应该是什么。

这些结果冇时非常容易猜到。例如从 $\mathrm{diff}(M)$ 我们有向量场的李括号而从辛流形 $(M,\omega)$ 有函数的 Poisson 括号。所以不用怀疑函数的辛括号概念与 $\mathrm{symp}(M,\omega)\subset \mathrm{diff}(M)$ 的向量场的李括号相关联。我们称这种关联为辛化。但在其它情况下复化，辛化或接触化是高度非平凡的。从某个理论幵始很难在其它理论中发现其相似物。

我曾发现一些例子。我毫不怀疑用这种方法获得的猜想是正确的。但是我不能证明它们。我能做的唯一事情是使用它们。而我真的成功地使用这些猜想很多次。这些推论是非平凡的定理但是我用来得到它们的方法是相当非逻辑的，因为没有公理精确地定义复。化或辛化意谓件么。只有猜想在你拿握之中、你构造猜想而且你能够试图去证明它。最终你或其他人证明了这些定理而这些获得的结果更坚定了最初的猜想。

这些例子。之一就是 Lagrangian 相交理论中的 Arnold 猜想²。这是我试图把通常拓扑的映射和向量场的指标的 Poincaré 定理推广到辛情形。在通常拓扑中有不动点的概念，Enler-Poincaré 定理是说一个流形的全部不动点的指标之和是个固定数、这个数被称为此流形的 Euler-Poincaré 示性数。我曾试图把它辛化并猜想它的答案是什么。我将详细地解释它。辛化的主要思想是去考虑模型。

你从一个流流 $M$ 开始。余切丛 $T^{\bullet} M$ 连同典则辛结构是与之相联系的辛流形。对任何子流形 $N \subset M$ 有一个 Lagrange 子流形 $L_{N} \subset T^{\bullet} M$ 对应它。去辛化一个光滑流形的子流形的几何只须去考虑 Lagrange 子流形的几何。

这就是所谓的 Weinstein 原理。 Alan Weinstein 曾这样叙述它：辛几何中每个有兴趣的对象是个 Lagrange 子流形，因为不动点及其指标当然是有兴趣的。$M$ 的通常相交理论的辛化一定能给出 $T^{\bullet} M$ 中的 Lagrange 相交理论。

下一步是忘掉模型流形结构而到一般辛流形。这样在六十年代我被引到应该存在辛拓扑和接触拓扑这个猜想，并且我开始发展它们³（Lagrange 相交理论，Maslov 类，Lagrange 和 Legendre 配边）。但是现在我不准备讨论这些，在下一个讲座中我将给一些具体的猜想和定理的例子，它们都是按这种辛化和接触化程序得到的。

在现在这次讲座我将讨论另一个题目，即非形式复化。这看起来要简单些因为每个人都知道什么是实数和复数。一个复向量空间可以认为是一个实向量空间配备了一个附加结构，即添加了乘以 $n$ 的算子。然而一个理论的复化并不仅是对空间的限制和引进一个新算子。所有几何概念都改变了。我们不是把复子空间和算子仅仅考虑成实空间的子空间和算子满足一些附加的性质。复几何并不是实几何的子理论而是独立的平行于实情况的姐妹理论。我将给一些非形式复化的例子和如何去用它。

当然实直线図的复化是复直线 $\mathbb{C}$。让我们来猜想什么是 Morse 理论的复化。在 Morse 理论中我们有非退化画数。它们在实情况是光滑的，在复情况必须考虑是全纯的。这样我们有临界点和临界值。如果我们考虑某临界值附近稍小的值和稍大的值，那么要从第一个值到第二个值我们必须加一个环柄。这是 Morse 理论中的主要工具，它描述一个非退化函数的正规水平集的修正。这里我们用到了实数可以比较大小这种可能性但对复数我们没有自然的不等式、复化将如何进行呢?

很显然函数点 $x^{2}+y^{2}$ 的复化应是是 $z^{2}+w^{2}$ 而临界点和临界值的复化后的概念是同样的。不同之处在于临界值的补在实情况是不连通的在复情况是连通的。在复情况不同正则值的逆像 (preimage) 拓扑地是相同的。没有环柄去添加。这时倩况如何呢？在实情况此临界值的补的零维同伦群是非平凡的：

$$ \pi_{0}(\mathbb{R} \backslash(0))=H_{0}(\mathbb{R} \backslash(0))=\mathbb{Z}_{2} $$

这与复情况相反。但在复情况我们要考虑映射 $S^{1} \longrightarrow \mathbb{C} \backslash\{0\}$ 的同伦等价类而下是映射 $S^{0} \longrightarrow \mathbb{R} \backslash\{0\}$ 的同伦等价类。所以 $\pi_{0}$ 的复化是 $\pi_{1}$ 而我们有：

$$ \pi_{1}(\mathbb{C} \backslash\{0\})=\mathbb{Z} $$

这样我们得到第一个非平凡: 事实即环 $(\operatorname{ring}) \mathbb{Z}_{2}$ 的复化是环 $\mathbb{Z}$。

现在我们知道在复情况对临界值如何去做。我们从——个正刚值开始，绕临界值一周再回到开始点这样我们看到实情况的环柄复化成了单值性（Monodromy）。Morse 理论的复化就是 Picard-Lefschets 理论⁴。在 $f(z, w)=z^{2}+w^{2}$ 这个例子中水平簇是个柱面，在它上面有个消没圈（vanishing cytlt）（它在临界时刻消没）。当你绕临界值 $0$ 一周你可以得到柱面的一个自同胚，它把消没圈映成自已但使整令拄面扭转。所以这个 Dehn 扭转，这个 Picard-Lefschetz 变换，是环柄添加结构的复化。从这个简单例子我们可以看到复化是多么不平凡。

让我们继续、实射影空间 $\mathbb{R} P^{n}$ 的复化是复的 $\mathbb{C} P^{n}$。特别 $S^{1} \simeq \mathbb{R} P^{1}$ 复化成 Riemann 球 $S^{2} \simeq \mathbb{C}P^{1}$。现在考虑同调，在上同调中我们有 Stiefel-Whitney 类 $w_{k}$。系数在 $\mathbb{Z}_{2}$ 中。他们的复化是陈类 $c_{k}$, 它属于的上同调系数在 $\left(\mathbb{Z}_{2}\right)_{C}=\mathbb{Z}$ 中。所以这些例子都是一致的。

现在魂将给一个应用这些复化思想的例子。1977 年左右 Pesrovky 清我帮助评价数学家 Gudkov 的一篇论文。他在研究 Hiibett 第 16 问题：对 6 阶平面代数曲线，$f(x, y)=0$，$\operatorname{deg} f=6$ 它的可能的形状是什么样？

对 2 阶的经典答案披 Newton 和 Descartes 分别推广到 3 阶和 4 阶。但之后困难开始了。Hilbert 没法解决 6 阶的情况。他把这个问题写进了他的 23 个问题中。也可以考虑它的仿射形式、但这更繁杂。倒是我们可以考虑该问题的射影形式。处理 $\mathbb{R} P^{2}$ 中的曲线。甚至对这个要简单些的问题，在 Hiibeer 那时候也没有答案。

唯一知道的事情是 Harnack 的著名定理。他证明了卵形线的个数 (曲线的零维 Betti 数）最多是亏格加一：$b_{0}(\Gamma) \leq g+1$。亏格由 Riemann 公式 $g=\frac{(n-1)(n-2)}{2}$ 来表示。对于 $n=6$ 我们有 $\max (b_{0})=11$。一条曲线如果达到最大可能卵形线数就被称为是 $M$ 曲线。Hibeet 提出了 6 阶 $M$ 曲线的卵形线的构形问题。

所有拓扑可能的构形由 11 个顶点的有根树标记。这样树的数目非常庞大。然而井不是其中每个树都对应存在 $M$ 曲线。比如考虑图 4 中的例子。由 Bézout 定理这是不可能的构形：6 阶曲线与某条直线有 8 个交点。

所以不是所有枸形是能瞽存在的。Gudkov 宣称得到了 6 阶曲线的所有卵形线构形表，但是 Petrovsky 怀疑他的结果，让我们来描述它。这个表包含 3 个 $M$ 曲线。其中毎个曲线恰好拥有一个非空（non-void）卵形线，其它卵形线有的在它里面，有的在它外面。对这三条曲线，在卵形线内和在外的数分别是：$(1,9),(5,5)$ 和 $(9,1)$。其他构形是不可能的。这是个奇妙的定理，它的证明很繁杂，很难理解。

图 4：$6$ 阶曲线不可能的卵形我排列

这篇论文是 Gudkov 的结果的第二个版本。在第一个中他检査了 $(5,5)$ 情形并证明其不存在。而在第二个版本中他显式地构造出了 $(5,5)$ 情形。他也构造了许多髙阶曲线。而整个图景还不清楚，但他对 $M$ 曲线做了些有趣的观察。

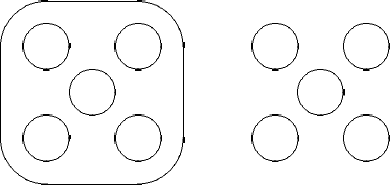图 5：对一个 $6$ 阶 $M$ 曲线，Gudkov 的 $(5.5)$ 悄形

让我们考虑 $(5,5)$ 情形，图 5 如果把 4 个卵形线从内移到外面或相反。那么得到 $(1,9)$ 情形或 $(9,1)$ 情形，而函数取止值的集的欧拉示性数变了 $8$。相反的过程也是同样的。所以 Euler 示性数模 $8$ 对 $M$ 曲线是恰当定义的。而且 $\chi \equiv k^{2}(\bmod 8)$ 对 Gudkov 能够构造的 $2k$ 阶 $M$ 曲线都可观察到。但对这种行为没有解释。

我知道模 $8$ 同余在 $4$ 维拓扑中是标准的。所以我想会在什么地方存在一个 $4$ 维流形。它主宰实平面曲线的拓扑。但如何去构造它呢？在这里复化进来了并非常有帮助。

从 $2$ 维到 $4$ 维显然需要复化。但是我们考虑的集合，即函数的正支集 (positivity support)，是个带边流形。这样问题变成去复化一个带边流形。当然假如有个超曲面，例如 $\{x^{2}+y^{2}=1\}$, 那么去复化它非常容易，在这个例子中：$\{z^{2}+w^{2}=1\}$。但假如是一个不等式 $f(x) \geq 0$ 定义了一个带边流形。复化的描述就不是这么显然。我是这样处理的。

让我们首先代数化，即写出不等式 $f(x) \geq 0$ 的代数形式。这是 $f(x)=y^{2}$。此方程等价于上述不等式，但是没有对复数没意义的符号了。在复数域上述公式定文了一个复流形的双重覆盖，这个复流形沿边界即沿一个复超曲面分歧。现在我们可以复化 $f(z)=w^{2}$ 的正域 (positivity domain)。这是带边流形的复相似物。它就是所需的 $4$ 维流形。

现在对此 $4$ 维流形我们应用 $4$ 维拓扑的所有工具，计算相交形式，示性类和其他拓扑不变量。之后我们回到实情形、把毎件事都翻译成卵形线的拓扑。这给出了 Gudkov 定理和其他很多高阶和高维的结果。

在我这第一步工作后不久，很多人继续发展了这些思想，实代数几何领域变成了一个非常繁荣的领域。这里我提到少许几个人，Rokhlin, Kharlamov，Viro，Nikulin, Sliustin 的重要工作。例如，Rokhlin 证明了 Gudkov 的模 $8$ 同余（我证明了只要模 $4$）、Kharlamov 找到了遇 $\mathbb{R} P^{3}$ 中 $4$ 阶超曲面的所有可能的拓扑类型，Nikulin 找到了这样超曲面空间的分支。 $8$ 阶曲线的形式还不知道。满足所有已知条件的情形总数最多足 $90$ 其中只有 $9$ 个的存在性还不清倉所以即使在 $8$ 阶也仍有挑战⁵。

复化的另一个例子同一篇关于二次型分层和单值性的文章，方式和拟方式（Modes and Quasimodes）有关。考虑欧氏空间二次型具有重持征值，即退化二次型。看起来好象这个条件给出一个方程 $\lambda_{1}=\lambda_{2}$，但它实际给岀更多。对二阶对称矩阵 $\left( \begin{array}{ll}{a} & {b} \\ {b} & {c}\end{array}\right)$。方程 $\lambda_{1}=\lambda_{2}$ 给出 $(a-c)^{2}+4 b^{2}=0$。所以一个方程 $\lambda_{1}=\lambda_{2}$ 等价于两个方程 $a = c$ 和 $b = 0$ 的方程组。类似地在任何欧氏空间在所有二次型中退化二次型所成子簇的余维数是 $2$ 不是 $1$。

例如假设我们有一个人造地球卫星，我们希望使修正的惯性椭球的两个轴相等。它成为旋转椭球。这样稳定性更好。假设我们的装备是。一个配重（Weight），它能沿一条直线运动。这还不够，我们确实还需要两个方向。

因为追化椭球所成簇的余维数是 $2$ 可以用等轴椭球来固绕这个簇。就好象环绕 $3$ 维空间中一条直线。在这个转动中可能发生一个倒转：两个轴改变它们的方向轴的长度保持不变，从一个椭球体的最大轴开始然后又回到这最大轴但是可能方向变成相反的。这通常要发生。这样得到了一个平坦联络，非退化椭球体空间的一个单值性。

现在考虑复化。这意谓着考虑 Hermitian 矩阵而不是正交阵。在 Hermitian 情况具有重特征值矩阵所成簇的余维数是 $3$，不是 $2$。补空间的基本群是平凡的。但是现在住横截空间（$3$ 维）有一个 $2$ 维球同重持征值子簇相连接（Linked）。而“方式和拟方式”的实理论的复化给出了量子力学中的 Berry 相理论和整量子 Hall 效应。

复化是大有前途的，也存在很多问题。例如我们考虑禪界概念的复化。这亍概念对同调是基本的。什么是同调的复化？这是个相当非平凡的问题，接下来还有定向，）$\operatorname{spin}^{\mathrm{C}}$ 结构等等。这里有丰富的顿域去探索，提出猜想，构造理论，但之后就是如何证明它们。

而且我们必须小心因为复化绝不是唯一的。同一个对象可能有数种复化。例如前面我们看到 $S^1$ 的复化是 $S^2$。但是让我们把 $S^1$ 考虑成群 $SO(2)$。$O(n)$ 和 $SO(n)$ 的复化显然是 $U(n)$ 和 $U(n)$。所以 $S^{1}=S O(2)$ 的复化最 $S^{3}=S U(2)$ 我们的流形 $S^1$ 被不同地复化了：一个情形是作为射影簇，另一个情形是作为一个李群。所以我们看到复化依赖于结构。

我这里也要提到 Coxeter 反射群的非形式复化，它们在我最近关于球函数的 Maxwell 拓扑定理的文章中出现，该定理把经典定理 $\mathbb{C} P^{2} / \mathrm{con} \mathrm{j}=S^{4}$ 推广到高维。这些复化是李群，它们可能给出 Chevalley 定理的一个奇怪的复形式。

最近由 Frenkel 和 Khesin 给出的环绕数的复化度量 $3$ 维复流形中拓扑不坏绕复曲线的“复环绕”⁶。此复环绕与超弦有关因此也与量子场论有关。流体动力学中螺旋不变量的复化肯定与 Chern-Siinons 泛函有关。但是这个关系还要形式化以便应用。

我想提岀的下一个梦想是一组更奇异的定理和猜想。这里我也没有理论。实际上这些思想更象是宗教而不是数学。核心的观察是在数学中我们遇到很多三元组。下面我将给出一组例子。我的主要梦想（或猜想）所有这些三元组由某个矩形交换图来统一。我是指存在某种“泛函”结构来连结不同的三元组。这些图的存在的知识提供了一些新的猜想，它们可能会成为真正的定理。

第一个三元组是毎个人都知道的:

$$ (\mathbb{R}, \mathbb{C}, \mathbb{H})\tag{1} $$

第二个是：

$$ \left(E_{6}, E_{7}, E_{8}\right)\tag{2} $$

这两个三元组的平行似乎是 Galois 理论中的一个非平凡定理，对此我没有解释，没有证明和公式。在几年前 Gelfand 五十寿辰会议上某些与此类似的事情被 Kazhdan 给出和证明，但我现在还没见到发表的版本。我想在 Kazhdan 的某篇文章中这些公式和证明能够找到。后面我将给出一个简化了的版本。

一个著名的三元组来自柏拉图理论。即：

$$(\langle\text{正四面体}\rangle, \langle\text{正八面体}\rangle,\langle\text{正二十面体}\rangle).\tag{3}$$

这些多面体的对称群是 Coxeter 群:

$$ \left(A_{3}, B_{3}, H_{3}\right).\tag{4} $$

几年前我发现一个运算把最后这个三元组变成 Coxetet 群的另一个三元组:

$$ \left(D_{4}, F_{4}, H_{4}\right).\tag{5} $$

后面我将描述这个相当意外的运算。

让我们继续。下面一个三元组的第一项是 Möbius 丛，即 $2$ 重覆盖映射把 Möbius 带边界映到中心线。第二项是它的复化，第三项是其四元数类似物。

$$ \left(S^{1} \stackrel{S^{0}}{\longrightarrow} S^{1}, \quad S^{3} \stackrel{S^{1}}{\longrightarrow} S^{2}, \quad S^{7} \stackrel{S^{3}}{\longrightarrow} S^{4}\right).\tag{6} $$

Möbius 丛的复化即是 Hopf 丛。从这构造显然在 Möbius 丛情形也应考虑底空间是射影空间而全空间是个群。对 Hopf 丛这是熟知的。这与先前的断言相一致，即当 $S^1$ 是射影直线时 $(S^{1})_C=S^{2}$ 而当 $S^{1}=S O(2)$ 时 $(S^{1})_C=S^{3}$。

接下来是单变量复多项式，Laurent 多项式和模多项式，即有三个极点 $0,1$ 和 $\infty$ 的有理函数。（如果扩大极点数目那么模数出现而 $3$ 个极点总能被规范）：

$$ \left(\mathbb{C}[z], \mathbb{C}\left[z, z^{-1}\right], \mathbb{C}\left[z, z^{-1},(z-1)^{-1}\right]\right).\tag{7} $$

Turaev 和 Frenkel 的最近一篇文章发表在“Arnold 和 Gelfand 讨论班”包含三元组:

$$(\langle\text{数}\rangle,\langle\text{三角数}\rangle,\langle\text{椭圆数}\rangle).\tag{8}$$

第一项是普通复数，第二个是其量子变形，它由带一个参数形变组成。第三个类型的数是两参数形变。

方式和拟方式理论引岀一个几何三元组：

$$(\langle\text{二次型}\rangle,\langle\text{Hermite 型}\rangle,\langle\text{超 Hermite 型}\rangle).\tag{9}$$

和

$$(\langle\text{平坦联络单值性}\rangle,\langle\text{向量丛曲率}\rangle,\langle\text{?}\rangle).\tag{10}$$

在两个三元组中头两项是熟知的。四元数向量空间中一个超 Hermite 型是个实二次型，它在单位四元数群 $S^{3}=S U(2)$ 作用下不变。在（10）中的第二顷可能超 Kähler 何方面专家会知道。曲率的复化应该是某种 $4$ 次形式，可称为超曲率，它应度量 Bianchi 恒等式失效的程度

我想前面提到的流形动力学螺旋性（渐近 Hopf 不变量）和 Chern-Simons 泛函之间的关系可能被补全构成一个三元组。但还不清楚第三碘应是较高维的还是较低维的。

接下来一三元组是由 Whitnty 类，Chern 类和 Pontryagin 类组成的著名的同调三元组⁷：

$$ \left(w_{i}, c_{i}, p_{i}\right).\tag{11} $$

Givental 提出了由同调，它的复化即 $K$ 理论和椭圆同调组成的三元组:

$$ \left(H^{\bullet}, K_{r}\langle\varepsilon l l\rangle\right).\tag{12} $$

现在我解释一下不同三元组间的一些关系。这种关系在很多情况下是非平凡的，我将只给出一些最简单的关系。首先考虑式中的多面体。计算一下边数。对正四面体边数是 $6$, 正八面体是 $12$, 正二十面体是 $30$。每个数都是相临整数的乘积：$6 = 2\cdot 3$，$12 = 3\cdot 4$，$30 = 5 \cdot 6$ 取第一个因子减一。我们得到第一个三元组（1）式中的关系：

$$ \begin{array}{ll}{\mathbb{R}} & {\mathbb{C}} & {\mathbb{H}} \\ {1} & {2} & {4}\end{array} $$

在大多数情呪里数字要复杂得多，但也象这个简单例子一样令人吃惊。要找到这些关系冇时需要艰苦的」工乍。例如考虑（W 式，在那儿我们不知道最后一项是什么。它必定是与 Pontryagin 数有关的某种 $4$ 次形式，也许是实局部平凡丛的某种四元数化, 或者是复局部平凡丛的复化。看起来找出所有这些关系是件非平凡的工作。

也许存在量子 Hall 效应的某种复化形式，三维横截被五维的代替。从复化“方式与拟方式”理论中的二次型的单值性理论应该很容易预言量子 Hall 效应和 Berry 相。但这个机会失去了。如果不研究“方式和拟方式”理论的四元数化，我们可能失去更多机会。

（3）式和（4）式的关系是显然的：后者由前者的对称群组成。但是与（5｝式的关系如何呢？首先考虑 $A_3$ 群。它由 $3$ 个镜面反射生成。但是全部镜面还要多些。找出正四面体对称群的整个构形和全部镜面反射数对学生是个很好的练习。答案是 $6$，因为每个边正好有一个镜面通过。但是要想象出 $3$ 维空间被这 $6$ 个平面的分解就不那么容易。即使数岀共有几部分也是个练习。答案是 $24$, 这正是 Weyl 群的阶，各部分被称为 Weyl 室。

因为每个镜面都包含 $\mathbb{R}^3$ 的原点，所以在射影平面上表示这些 Weyl 室更好些。所以在射影平面上右 $6$ 条线，不难画出这个图形（现代语言的描述〕它被表示在图 6，左边（译者注：此图可能有误）。

图 6：$A_3$ 群的 Springer 锥和它们分解成 Weyl 室

$\mathbb{R}^3$ 中每对相对的 Weyl 室由一个三角形表示。每个 Weyl 窒的墙构成了 $6$ 条线中的 $3$ 条。其它 $3$ 条被加到左边的图上。它们总共把射影平面分成 $12$ 个三角形。所以 $\mathbb{R}^3$ 中 Weyl 室的总数是 $2\cdot 12 =24$。

让我们更详细地描述这个分解。一个 Weyl 室的墙构成了 $\mathbb{R}^3$ 中的三个平面并将它分成 $8$ 部分。我称它们为 Springer 锥（因为 Tony Springer 从没考虑过它们）对任何 Weyl 室，它的墙把 $n$ 维空间分成 $2^n$ 个 Springer 锥。每个 Springer 锥包含几个 Weyl 室，如图 6。空间分解成 $8$ 部分在射影平面被表示成分解成 $4$ 部分。每个对应二个相对的锥。延拓一个 Weyl 室的墙我们得到射影平面分成 $4$ 个（Springer）三角形，现在我们数一下不同部分包含的 Weyl 室的数目得到整个 Weyl 数的分解：$24 = 2(1+3 + 3 + 5)$

如果对正八面体做同样的工作我们得到下列 Weyl 数的分解：$48 = 2(1+5+7 + 11)$。对正二十面体我们得到：$120 = 2(1 + 1 + 19 + 29)$。

如果你熟悉 Coxeter 群你会知道 $D_4$ 的拟齐次权。它们们是 $(2,4,4,6)$。如果把这些数与上述 $24$ 分解岀的数比较，那么对 $F_4$ 的拟齐次权是 $(26,8,12)$ 就不会感到奇怪。现在假如你对 $H_4$ 毫无了解你也会猜到它的拟齐次权是 $(2,13,20,30)$。这样我们就发现了（4）式和（5）式的一个关系。

在其他情况这个平行性可能更奇怪。这里我加上在文具店里出售: 的三角形听构成的三元组：

$$ ((60,60,60),(45,45,90),(30,60,90)).\tag{13} $$

前面描述的理论建议其中第二项是第一项的非形式复化而第三项是四元数化。但是这个猜想同这个陈述即正八面体是正四面体的复化而正二十面体是它的四元数化一样神秘。

问题 什么畀 Kazzr 柱的复化？即是指柱面上的函数。

回答 实三角多项式层化（Stiatfcateion 理论的复化是复三角多项式层化理论。它也许能在“Functional Analysis”1996 中找到。一定也会有它的四元数化。

Springer 锥理论是复 $\mathrm{L} 2$（Lyashko-Looijenga）映射的实形式，该映射映单变量复多项式到它的临界值的无序集。 $\mathrm{L} 2$ 映射的复三角多项式形式是 $\mathrm{L} 3$（Lyashko-Looijenga-Lcurent）映射。我们可以试图考虑实三角多项式理论作为 Springer 锥论的一个仿射 Coxeter 群 $\tilde{A}$ 变形，尽管 Dubrovin 关于仿射 Coxeter 群的工作联系到共形弦论的 Frobenius 簇。为了试图去找到 Springer 锥论的这种推广我构造了实三角 $M$ 多项式分层簇的一个多面体模型。但是这些多面体模型与 Dubrovin 仿射 Coxeter 群的关系仍然是猜想性的（或许要得到 Springer 锥论的三角情形应该应用 Dubrovin 的构造到实形式，它与 Dubrovin 所研究的复的情形所对应的实形式是不同的）。

\(\mathrm{L} 3\) 映射的复理论的实形式与 Kazar 定理有关。我们也可以考虑圆柱 $S^{1} \times \mathbb{R}$ 的另一种复化，是由 A. Tyurin 向我建议的。它是 $S^{3} \times \mathbb{R}$ 确实，$S^1$ 在 $\mathbb{C}$ 中的邻域是 $S^{1} \times \mathbb{R}$，而 $S^3 = (S^1)_C$ 在 $H = (\mathbb{C})_C$ 中的邻域是 $S^{3} \times \mathbb{R}$ 也应该存在 \(\mathrm{L} 3\) 映射的带 $3$ 个奇异点的模形式。但到目前还没有构造出来。

问题 3 个奇异点的情形是与四元数有关吗？

回答 当然与四元数有关，但我还不知道这关系是什么。

问题 Gudkov 的论文得到推荐了吗？

回答 这篇论文当然得到了辨护，尽管我一点也读不懂它。但作为结果我发现了上述我解释过的所有东西。我艰苦工作了一个月，之后我证明了他的猜想模 $4$。其中最困难的事情是个引理我能猜到但不能证明。我总是有非常好的研究生，在当时我请 Varchenko 帮助我。一周后他交回了该引理的证明，这允许我继续工作。但当我快结束时我发现 Varchenko 的证明是错的。这是个灾难，因为每件事都依赖该引理。我不得不重新开始艰苦地工作去证明该引理，最后我成功了。但是如果没：有 Varchenko 关于该引理正确的论断我不可能完成余下的工作，会停住该引理处。很遗憾 Varchenko 不愿在最后的文章上署名做为合作者。

D. A. Gudkov 成为了实代数几何方面一个很强队伍的领导者 (Utkin, Polotovskii, Shustin)，Gudkov 和他的学生的一些结果最近被 C. T. C. Wall 重新发现。不久前美国数学协会岀版了一卷 Gudkov 纪念集。那里能找到他不平凡人生的传记和他对实代数几何大量贡献的播述。

注

（1）Manin 有一次告诉我为什么在很多不同的数学分类中总是遇到这个表的原因是它存在于我们大脑的硬件中 (这使我们不能发现更复杂的格式）。我仍然希望某一天会发现更好的原因。

（2）似乎在曲面情开形勺“Arnold 猜想”的第一个 (正确的？) 证明由 Eliashberg 在 Syktyvkar 于 1978 年发表（在我在七十年代否定了它的四个原始版本之后）（现在仍没有该文章的英译文但 Eliashberg 已经保证很快会发表）。后来在 Gonley 和 Zehnder（1983）的著名的文章之后——该文章以 Rabinowitz 的思想为基础，出现了由 Chaperon, Chekanov，Floer, Giveutal，Gromov，Hofer, Laudenbach, Sikorav，Viterbo, Weinstein 和很多其他人作出的许多重要的贡献。量子和 Floer 上同调是这个发展的副产品。从第一次尝试之后，出现了不同的形式推广我最初的猜想，即通过流形上函数的临界点的最小数缩小紧辛流形的精确 (exact) 辛同胚的不动点数。去年我被告知这个原始猜想已被 Fukagaono，Salamon，Ruan 和其他人证明了。然而我没法检验这些技术上非常困难的证明。 Kontsevich 在我在巴黎的讨论班上没能报告这些细节。而所冇这些证明都以他的关于稳定曲线的引理为基础。

所有这些结果在辛拓扑是非常重要的。但对我来说似乎我 1965 年的猜想一关于高维圆坏的辛同胚的不动点数，它推广了 Birkhoff-Poincaré 定理，以及在“辛拓扑初步”（1986）这篇文章中关于辛对应和关于待征弦的猜想仍然没有解决。

（3）我将强调指出 Gromov 和 Eliashberg，他们是这个新领域的最初探索者，使用不同的辛拓扑和接触拓扑槪念。他们是指辛几何和接触几何中对象的同胚不变量的研究。而对我来说辛和接触拓扑是对辛和接触几何中连续对象的离散不变量的研究，它们也可能是同胚不变量也可能不是。以这同样的方法我把连续 (光滑) 对象的离散不变量包括进了微分拓扑，它们不是同胚不变的。

（4）根据最近 V. Vassiliev 的文章“具有扭系数 (twisted coefficients) 分层 Picard-Lef-scheetz 理论”，[Topics in Singularity Theory A. Khovomsky, A. Varchenko, V. Vassiliev 编，Advances in the Mathematical Sciences-34 (AMS Translations 180), Providence RI (1997). 241-255 页]，Goresky-Macpherson 分层 Morse 理论证复化是分层 Picard-Lefschetz 理论，它推广了 F. Pham 的理论，以及双曲偏微分方程中空隙问题的 Petrovsky 的 Cycle Crucial 理论。

（5）俄国的方式去提岀问题或猜想是提出最简单的未知情形，使进一步证简化是干可能证。这与法国提出问题的方式相反，在那里问题以如此一般的形式出现以至没人能再进行一般化了。

（6）看 B. Khesin 的文章“模空间的非形式复化和 Poisson 结构”[Topics in Singularity，同（4）. 147-155 页] 和该文所引用的他和 I. Fredzel, A. Todorov, A. Rosly, V. Fock 的文章。

（7）这次多伦多讲座之后 Gabrielov 告诉我在他同 Gelfand，Losik 和 Mcpherson 研究的 Chern 和 Pontryagin 形式的多对数表示中将分别遇到带 $2$ 和 $3$ 个极点证有理函数。这肯定了三元组（7）和（11）证平行、但是 Whitney 类和普通多项式，即一个极点的情况的关系仍是个秘密。

作者:	V. I. Arnold
译者：	于徳隆
校订：	卞纪
来源：	《数学译林》1999 年第 2 期