细心的读者也许注意到了，在介绍欧几里得与《几何原本》时，有一条也许是整部《几何原本》中最吸引眼球的命题未曾展开说明，那便是大名鼎鼎的“公设 5”——也即第五公设。不过当时说过“不久之后会有单独介绍”，现在就让我们兑现许诺，来介绍一下第五公设及对它的探索。为避免偏离时间顺序太远，我们的介绍将只涵盖早期探索—确切地说，是所谓非欧几何诞生之前的探索。至于非欧几何，则将留作未来话题。

在《几何原本》的煌煌 13 卷中，内容分布大体是这样的：第 1~4 卷主要为平面几何，但间杂了数的理论——比如第 2 卷给出了乘法对加法的分配律等，并求解了若干代数方程；第 5~6 卷为比例理论及相似理论，但同样间杂了数的理论，且关于数有很深刻的洞见；第 7~9 卷以对数学分支的现代分类观之，是对几何与数的相对比例的的逆转——转入了以数为主的数论范畴，其中包括了对素数有无穷多个等重要命题的证明 (第 9 卷命题 20)；第 10 卷延续了以数为主的局部“主旋律”，对“不可公度量” (incommensurable)——也就是无理数——做了详细讨论[注一]；第 11~13 卷重返几何，但由平面走向立体，以对包括“柏拉图正多面体” (Plato solid) 在内的诸多立体几何话题的探讨结束了全书。

前文主要介绍了我们对欧几里得的了解——或许只是在“不了解”也是一种了解的悖论意味上，以及《几何原本》的流传及版本沿革，接下来让我们对《几何原本》本身略作介绍。 作为一部示范了公理化体系巨大威力的著作，《几何原本》一开篇——即第 1 卷——就展开公理体系，不带一个字的多余铺垫，直接就列出了 23 个定义， 5 条公设和 5 条公理。这是迥异于柏拉图和亚里士多德，乃至迥异于一切哲学著作的风格。

在介绍柏拉图时，我们曾经说过，“虽著作广为流传，我们对柏拉图的生平却知之甚少”，这一特点在柏拉图那里只是稍带戏剧性，到欧几里得 (Euclid) 这里则堪称达到了极致。用“知之甚少”已不足以形容我们对这位留下《几何原本》 (The Elements) 及其他数种著作，被尊为“几何之父” (Father of Geometry) 的伟大先贤的生平了解之贫乏。

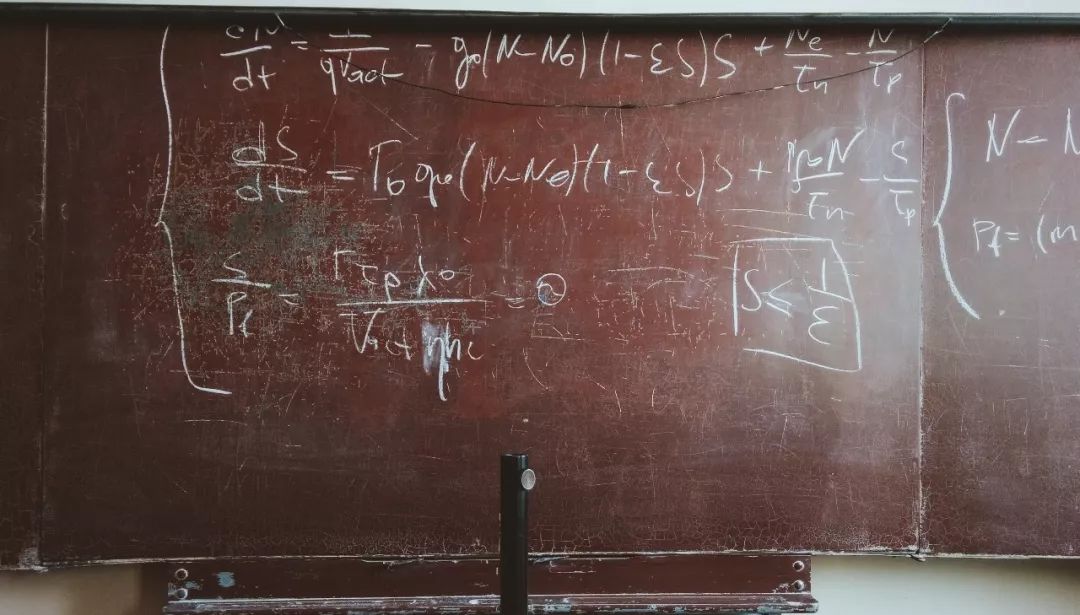
从幼儿园小班到高中毕业，我国大部分青少年要和数学打大约 15 年的交道；若是进了大学的理工科，还要再与高等数学打几年交道；如果将来的志向是当数学教授，则要打一辈子交道了。多年来，由于奥数的大举入侵，数学似乎成了许多学生成年前最花心血的一门学科。照理说，校园内外有这么浓厚的数学氛围，我们的学生应该是数学的宠儿了，但是我经常听说大学理工科的许多学生十分怨恨数学，也没有真正学好数学，甚至包括数学系的那些理想成为职业数学家的新生。

我的一位发小和我一样有保存老物件的习惯，他知道我的这个爱好，专门托人从北京带来了一把老式的尺子，非常漂亮。这把尺子就在我的起居室的茶几上。每次看到它就觉得应该写点什么。今天我们就来说说尺子里的数学。具体地说，我们要讲的是一种叫哥隆尺的数学概念，同时看看它有什么实际的应用。

近些年来，中小学的数学教育引起了世界各国的数学家的广泛关注，其中的代表者有：俄国的阿诺尔德（Arnold【2，3】），美国的巴斯（Bass【5，6】），匈牙利的罗瓦兹（Lovász【16】），中国的吴文俊（【26】）、姜伯驹（【14】）等。这里我们要介绍的是美籍华人伍鸿熙（Hung-Hsi Wu）关于中小学数学教育的理念与工作。

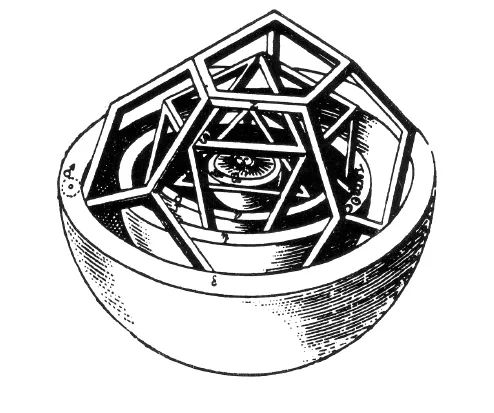
古人虽然感觉到只有五种柏拉图多面体，但却没有证明。关于这个问题，基于欧拉多面体公式，可以得出一个非常简单的证明。注意观察正多面体的边，每一个边都是由两个顶点规定了的，且每一个边又都是由两个面所规定了的—两个顶点连一个边，两个面交于一个边。

在这一轮课程改革中，“数学与文化”成为了数学和数学教育工作者最为关注的问题之一。实际上，在很长一段时间内，许多数学和数学教育工作者已经在思考和研究这个问题，在即将推行的“高中数学课程标准”中，明确的要求把“数学文化”贯穿高中课程的始终。

天上有多少颗星星，数学中就有多少个未解之谜。如果要我从数学中选出一颗最神秘的星星，那我一定会选著名的 3n+1 猜想。