细心的读者也许注意到了，在介绍欧几里得与《几何原本》时，有一条也许是整部《几何原本》中最吸引眼球的命题未曾展开说明，那便是大名鼎鼎的“公设 5”——也即第五公设。不过当时说过“不久之后会有单独介绍”，现在就让我们兑现许诺，来介绍一下第五公设及对它的探索。为避免偏离时间顺序太远，我们的介绍将只涵盖早期探索—确切地说，是所谓非欧几何诞生之前的探索。至于非欧几何，则将留作未来话题。

第五公设之所以引发探索，在一定程度上是拜五条公设的表述繁简之别所赐。为了看清这一点，我们将《几何原本》中的五条公设罗列于此：

1. 在任意两点之间可作一直线。

2. 线段（有限直线）可任意延长。

3. 以任意中心及任意距离（为半径）可作一圆。

4. 所有直角彼此相等。

5. 若一条直线与两条直线相交，且同侧的内角之和小于两直角，则那两条直线任意延长后会在内角之和小于两直角的一侧相交。

既然罗列了公设，那么顺便说明一下，《几何原本》对公设的表述有一些细节上的瑕疵。比如有些隐含之意未被述及。具体地说，公设 1 没有述及在任意两点之间可作的直线是唯一的，公设 2 没有述及线段延长的方式是唯一的，第五公设未述及三条直线位于同一平面这一先决条件。此外，同时使用“直线”和“有限直线”这两个术语，似乎意味着“直线”是无限的，其实却不然—否则就不会有第五公设中“两条直线任意延长”的说法了。

但撇开瑕疵不论，任何读到上述五条公设的人几乎必然会注意到的一个特点是：第五公设与前四条公设相比实在太繁复了，简直就像一条定理。虽然从逻辑上讲，公设（以及公理和定义）无非是一个公理体系的推理起点，繁复与否并不妨碍功能。但自古以来，对公设（以及公理）的一个重要判据就是自明性—或者用亚里士多德的话说，必须是明显为真却无法证明的命题，而表述繁复会损及自明性。

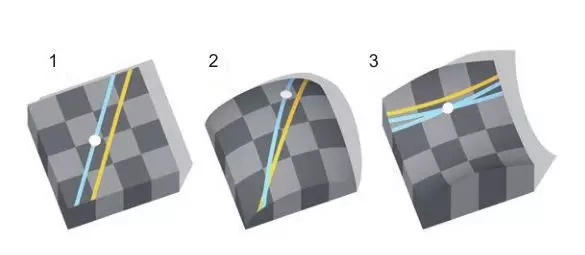
第五公设是欧几里得几何（平面几何 1）与非欧几何（球面几何 2、双曲几何 3）的分野：在球面几何（又称黎曼几何）中，过直线外的任意一点没有直线能与之平行；在双曲几何（又称罗巴切夫斯基几何）中，过直线外的任意一点至少有两条直线与之平行。

第五公设的情形正是如此。

这一点引起了很多后世数学家的批评乃至不满。比如 17 世纪的英国数学家亨利・萨维尔（Henry Savile）和 18 世纪的意大利数学家乔瓦尼・萨凯里（Giovanni Saccheri）都表示，第五公设是除此之外堪称完美的几何公理体系的唯一瑕疵。

不过，对第五公设的批评或不满虽很普遍，但除了从类似芝诺悖论的角度出发的极个别质疑者外，早期探索者们大都认同第五公设作为命题的正确性，只是对它是否该被列为公设怀有疑虑。比如公元 5 世纪的希腊哲学家普罗克洛斯（Proclus）就表示，第五公设的结论是可信的，只是“应该从公设中剔除出去，因为它是一条困难重重的定理”—这也是几乎所有早期探索者的共同判断。

那么，除了表述繁复损及自明性这一泛泛观感外，普罗克洛斯作出这样的判断有没有更具体的理由呢？答案是肯定的。主要的理由有两条：一是第五公设的逆命题和否命题的表述繁复程度与第五公设相若，却都是定理——前者是命题 17，后者是命题 27 和 28；二是普罗克洛斯认为自己能证明第五公设。

普罗克洛斯的这两条理由在早期探索者中有很大的代表性，下面我们就以这两条理由为线索，来介绍一下对第五公设的早期探索。

先说说第一条理由。这条理由是推测性而非证明性的—因为逆命题和否命题跟原命题并不等价，因此，即便逆命题和否命题都是定理，也并不能证明原命题也是定理，甚至连原命题是否成立都不能保证。尽管如此，这种推测性的理由对于引导—或引诱—人们怀疑第五公设的公设地位，进而展开探索却有一定的推动作用。这种推测性的理由除普罗克洛斯给出的这一条外，其他人也提出过。比如很多人注意到了第五公设在《几何原本》中直到证明命题 29 时才被使用，比其他公设的使用晚得多。具体地说，公设 1 和公设 3 在证明命题 1 时就被使用，公设 2 在证明命题 2 时就被使用，公设 4 虽较晚，直到证明命题 14 时才被使用，跟第五公设相比仍早得多。这一情形使很多人猜测欧几里得本人对第五公设的公设地位也有疑虑，因而尽可能延迟了它的使用。

不过若对《几何原本》第 1 卷的命题作更细致的分析，针对所谓“延迟使用”的上述解读就会削弱许多。因为《几何原本》第 1 卷对命题似乎有一定的分类，体现在命题 1～26 多为有关简单作图及三角形简单性质的命题，直到命题 27 开始才涉及平行线及其性质（此后很快便在证明命题 29 时使用了第五公设）。因此，假如欧几里得在命题编排上存在分类方面的考虑，也会造成第五公设被延迟使用的情形，那样的延迟就未必有其他深意。事实上，在称得上现代版《几何原本》的德国数学家大卫・希尔伯特（David Hilbert）的名著《几何基础》中，平行公理（即“第五公设”的现代名称）的使用甚至比《几何原本》更晚，直到证明命题 30 时才被使用，那便纯系命题分类所致（希尔伯特将平行公理安排为第 4 组公理，“出场”次序亦由此而定），而并无其他深意。从这个角度看，仅仅因延迟使用而猜测欧几里得对第五公设的公设地位有所怀疑，不是很有说服力。

不过另一方面，虽然所谓延迟使用未必有深意，但确实有其他迹象显示欧几里得有可能并不是一开始就将第五公设视为公设的，因为在《几何原本》的某些抄本中，第五公设未被列为公设，而是作为一个普通命题出现在命题 29 之前。假如这些抄本源自欧几里得本人的早期版本，那么就有可能意味着欧几里得曾一度将第五公设的内容视为普通命题，后来，多半是因无法证明才改列为公设。若如此，这或许也解释了第五公设的表述为何像一条定理（不过对这一点，后文会提到一条也许更有可能的理由）。同时，它直到证明命题 29 时才被使用也就确实没什么深意了，因为作为普通命题时就是被安排在那个位置上的。当然，这些都只是猜测。

也许，怀疑第五公设的公设地位的最有力理由，归根到底还是表述繁复损及自明性这一泛泛观感。事实上，哪怕持其他理由的人，恐怕也是首先被第五公设的表述繁复引起了疑心。我曾经设想：倘若欧几里得对第五公设的表述不是那么繁复，而代之以等价表述之一的“普莱费尔公理”（Playfair′s axiom），即“过直线外的任意一点只有一条直线与之平行”，也许第五公设就不会那么吸引眼球，从而也不会引发那么多探索了。不过，在数学史来看，对第五公设的探索导致了非欧几何的诞生，对数学乃至物理学的影响都极其深远。从这个角度讲，第五公设的繁复可谓“劳苦功高”，而且这功劳在很大程度上可归于欧几里得。因为《几何原本》的很多内容虽来自前人，第五公设的这一繁复表述却与欧几里得之前的所有已知著述存在显著差别，从而被认为是出自欧几里得本人的。仅此一条，欧几里得就可跻身大几何学家的行列。

荷兰艺术家埃舍尔的版画《圆极限 III》，体现了双曲几何的特征，其中的每一条曲线都是曲面上的直线。

但是，欧几里得为何采用如此繁复的表述呢？如今只能猜测了。上文已提到过一种可能的解释，一条也许更有可能的理由则是：“过直线外的任意一点只有一条直线与之平行”是不能在有限范围内确认的，因为无论检验过多大的范围，两条看似平行的直线都仍可能会在检验范围之外相交。而欧几里得的表述所着眼的“相交”则可在有限范围内确认，从而可避免触及无穷这一概念。在欧几里得时代，乃至在有关无穷的严密框架问世之前的所有时代，避免触及无穷都是规避逻辑困境和诘难的有效途径。有些数学史学家及哲学家甚至认为，整个古希腊数学大体上都是奉行有限主义，或起码是排斥所谓“实无穷”的。不仅如此，有限主义哪怕在现代数学哲学中也不乏追随者。

因此，欧几里得有可能是出于古希腊数学所奉行的有限主义而将第五公设表述得如此繁复。当然，这仅仅是猜测。

以上是由普罗克洛斯的第一条理由引出的介绍，接下来再谈谈他的第二条理由——即“认为自己能证明第五公设”。这种“认为自己能证明第五公设”的感觉可以说是早期探索的真正主宰，由此引发的是数学史上历时最久的努力之一：“证明”第五公设。从欧几里得时代算起，直到因非欧几何的诞生而尘埃落定，这一努力跨越了两千多年的时间。与之相比，曾经是猜想或依然是猜想的哥德巴赫猜想、孪生素数猜想、费马猜想、四色猜想、黎曼猜想等都只能算“小年轻”了。

在下篇中，我们将介绍几个有代表性的“证明”。这些“证明”不仅是对历史的一种勾画，而且也揭示了欧几里得几何的某些重要性质。