早在数千年之前，巴比伦人就已经发明了乘法。而就在上个月，数学家们又对这一运算方式进行了优化，使它越来越完美。

3 月 18 日，两位研究人员有可能发现有史以来最快的计算两个超大数的乘法运算方式。这篇论文的诞生，也意味着数学界最基本的运算方式又有了更新更有效的运算过程，有望破解了一个已经存在近半个世纪的数学问题。

法国国家科学研究中心数学家，这篇论文的共同作者之一 Joris van der Hoeven 说道，“大部分人都以为自己在学校里面学到的方法就是最好的方法，但是实际上在研究界，有关乘法的计算方法领域一直是十分活跃的，而且不断有着新的突破和优化。”

有史以来最快大数相乘算法的两位发明人，上为法国国家科学研究中心的数学家 Joris van der Hoeven ，下为新南威尔士大学教授 David Harvey。在计算超大数时，下图中的传统计算方法会变得十分吃力（来源：École Polytechnique）

许多数学计算领域的难题，从圆周率的计算到寻找最新的更大的素数等等，其运算复杂性最终都将由为基本的乘法的运算速度决定。Van der Hoeven 认为，许多其他类型的问题理论上可以达到的最快的被解决的速度极限，最终也都将由乘法的运算速度决定。

“物理学中也有一些十分重要的常量，比如光速就是决定许多其他物理现象的基本参数”，Van der Hoeven 说，“如果你想知道计算机解决各种数学问题的速度有多快，那么整数乘法的运算速度也将是回答这一问题的一个基本参数，描述计算机的许多种运算的速度都将会用到这个参数。”

大多数人所学乘法的运算方法都是以下这种方法。将两个乘数排成两行，用下面的乘数中的每一位数字分别去乘以上面的乘数的每一位数字，然后将所有的相乘结果相加。比如说，如果是两个两位数的乘法运算，你需要进行四次两个一位数的相乘，然后将这四个相乘的结果相加。

这个我们在小学就学过的乘法的算法，即竖式计算乘法的方法，在进行 $n$ 位数之间的相乘时，需要进行大约 $n$ 的平方次个位数的相乘，这里 $n$ 是每个乘数的位数。所以，两个三位数的乘法需要进行 9 次个位数的相乘，而如果你要进行的是两个 100 位数的大数相乘，就需要 10,000 次个位数的相乘。

传统的竖式计算方法（来源：互联网）

上面说到的竖式计算方法，其实更适用于位数少的数字之间的相乘。当我们需要进行数百万位数或数十亿位数的乘数之间的相乘时，竖式计算方法就显得无能为力了，例如计算圆周率或者寻找更大的质数。

如果要将两个 $10$ 亿位数的数字相乘，需要进行十亿的平方次个位数的相乘，这个运算需要现代计算机花费大约 30 年的时间。

在过去的数千年以来，人们都认为没有比竖式计算方法更快的乘法的算法了。

直到 1960 年，一位名叫 Anatoly Karatsuba 的 23 岁的俄罗斯数学家参加了由 20 世纪最伟大的数学家之一 Andrey Kolmogorov 领导的研讨会。当时，Kolmogorov 断言，没有一种方法可以以少于 $n$ 的平方次个位数之间的相乘来完成两个 $n$ 位数之间的相乘。但是 Karatsuba 认为有；然后仅仅经过了一周的探索，他就找到了这种方法。

高能预警， Karatsuba 提出的算法思路如下：

计算 25 乘以 63，传统的算法如下需要 4 次个位数之间的相乘以及几次加法，如下：

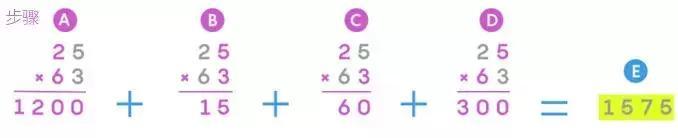
Karatsuba 算法需要 3 次个位数之间的相乘以及几次加法和减法，如下：

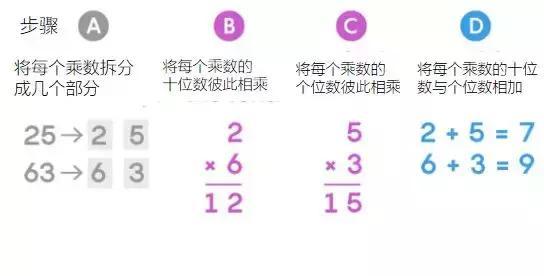
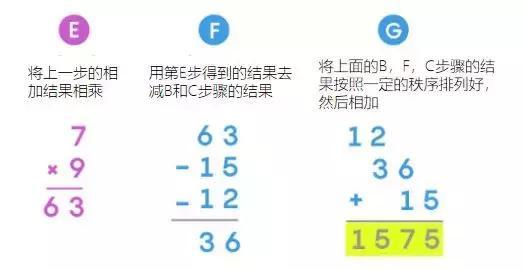
后者看似步骤比较多，但其优势在特大数相乘时就显现出来了，主要体现在节省个位数之间相乘的次数上：当乘数的位数很多时，可以重复进行 Karatsuba 过程，将原来的乘数拆分成更小的部分。所进行的拆分的次数越多，相比传统算法，你就节省了越多次个位数之间的相乘。

例如，计算 2531 乘以 1467，传统的算法需要进行 16 次个位数之间的相乘，如下：

而 Karatsuba 算法只需要进行 9 次个位数之间的相乘，如下：

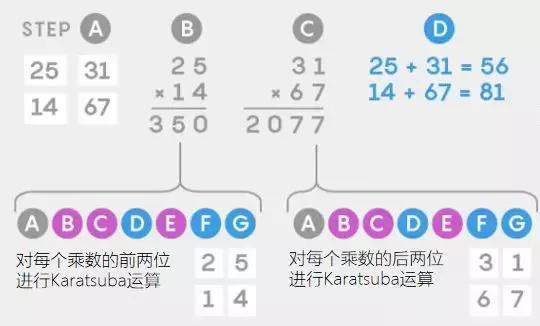
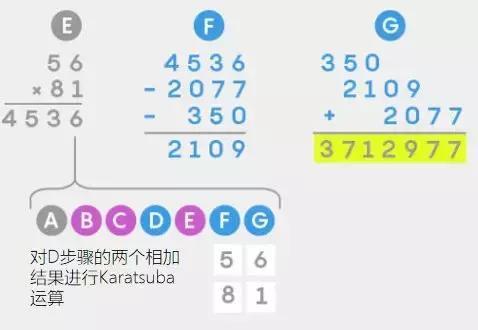（来源：quanta）

由此也可以看出，Karatsuba 的算法的主要想法是分治算法，也就是将大数的乘数分解成更小的部分，并以一种新颖的方式重新组合这些部分，这种方式可以用少量的加法和减法来代替大量的乘法。Karatsuba 算法节省了时间，因为完成加法计算时仅需 $2n$ 步，而不是 $n^2$ 步。

宾夕法尼亚州立大学数学家 Martin Fürer 说道：“另外，比起竖式计算方法，你可以在学校里提前一年学会这种方法，因为这种方法更容易，你可以在线性的时间内快速完成运算，这几乎和从右到往左阅读数字一样快”。Martin Fürer 在 2007 年也创造了当时世界上最快的乘法算法。

在处理大数乘法时，可以重复进行 Karatsuba 过程，将原始数字拆分为几乎与数字的位数一样多个部分。通过每一次拆分，你都可以将本需要许多许多次的乘法以需要的运算次数少的加法和减法来替代。

新南威尔士大学的数学家，同时也是这篇新论文的共同作者之一 David Harvey 说：“Karatsuba 算法可以把一些乘法变成加法，而对于计算机来说加法会更快。”

使用 Karatsuba 的方法，可以达到在 $n^{1.58}$ 次个位数的乘法后，完成两个 $n$ 位数的乘数之间的相乘。然后在 1971 年，Arnold Schönhage 和 Volker Strassen 发表了一种能够以 $n×\log n×\log (\log n)$次个位数的相乘来完成大数相乘方法，其中 $\log n$ 是 $n$ 的对数。而利用 Karatsuba 的方法进行两个 $10$ 亿位数字之间的相乘时，则大约需要 $165$ 万亿个额外的步骤。

（来源：此次论文）

Schönhage 和 Strassen 的大数相乘的算法，对之后的大数相乘算法的发展产生了两个重要的长期影响。

首先，它头一次在大数相乘领域将一种来自于信号处理技术领域的被称为快速傅立叶变换的方法引入了该领域。之后的每一次快速乘法算法都以这种方法为基础。

另外一个重要影响是，在同一篇论文中，Schönhage 和 Strassen 推测道，应该有一个比他们所发现的算法更快的算法——一种只需要 $n×\log n$ 次运算的方法，而且这种算法将会是最快的算法。他们的推测主要是基于一种预感，因为他们觉得大数乘法的最少的基本操作次数应该比 $n×\log n×\log (\log n)$ 这个公式更优雅。

“这其实是一种很普遍的共识，人们都认为既然乘法是一个如此重要的基本操作，那么从美学的角度来看，这样一个重要的操作需要一个很优雅的复杂性极限的描述公式”，Fürer 说，“从普遍经验来看，最最基本的事物的数学描述总是十分优雅的。”

不过，在之后的 36 年里，都没有人找到比 Schönhage 和 Strassen 这个不那么优雅的需要 $n×\log n×\log (\log n)$次基本运算的算法更快的大数乘法的算法。

（来源：quanta）

直到 2007 年，Fürer 终于打破了这一领域一直没有进展的状态，而这次发现仿佛打开了人类这在一领域发现的阀门一般。在过去的十年中，数学家们不断的相继发现更快的乘法算法，而且每种算法都比之前更接近 $n×\log n$，但是却一直没有完全达到它。直到上个月，Harvey 和 van der Hoeven 终于达到了。

他们的方法是对之前的主要方法的一种改进和优化。他们的方法也会分割数字，使用快速傅立叶变换的改进版本，而且他们还利用了过去四十年间这一领域其他进步的成果。van der Hoeven 说，“只不过我们以更激进的方式来使用快速傅里叶变换，我们的方法要进行多次快速傅里叶变换而不只是一次，而且也用加法和减法代替更多的乘法。”

Harvey 和 van der Hoeven 的算法证明了乘法可以进行 $n×\log n$ 次基本乘法来完成。但是，他们并不能证明没有比这种方法更快的算法。要证明这种方法是最好的方法要比发现这一算法困难得多。2 月底，奥胡斯大学的一个计算机科学家小组发表了一篇论文，认为如果另一个未经证实的猜想成立的话，这一方法将可以被证实确实是乘法的最快的算法。

虽然这一新的算法理论上将有着重大意义，但实际上比起之前的算法，它其实并没有进行太大的变化，它只比已经在被我们使用的算法稍微好一些。

“使用这种算法，最好的情况下也只比之前的算法最快三倍”，van der Hoeven 说。“这并没有比之前快很多。”

此外，计算机硬件的设计也在过去几年间发生了许多变化。二十年前，计算机执行加法要比乘法快很多。但是乘法和加法之间的运算速度的差距在过去 20 年中已经大大缩小，在某些芯片架构中，乘法甚至比加法更快。在使用某些硬件时，“你甚至可以让计算机通过做多次乘法来提高加法的运算速度，这在之前简直的不可想像的”，Harvey 说。

不过，硬件随时间在不断发展，但是对于一种运算的最佳算法的寻找却是是永恒的没有尽头的。无论计算机在未来会变成怎样，Harvey 和 van der Hoeven 的算法将一直会是最有效的乘法运算方法之一。

新算法的长图版（来源：quanta）

参考：

https://www.quantamagazine.org/mathematicians-discover-the-perfect-way-to-multiply-20190411www.quantamagazine.org

https://hal.archives-ouvertes.fr/hal-02070778/document