《数学家讲解小学数学》简介前篇:伍鸿熙教授谈中小学数学教育存在的主要问题
 《数学家讲解小学数学》,伍鸿熙著,赵洁、林开亮译,北京大学出版社,2016 年
《数学家讲解小学数学》,伍鸿熙著,赵洁、林开亮译,北京大学出版社,2016 年
数学课要讲得孩子们有兴趣。孩子们都是有好奇心的。他们对数学本来也有好奇心。可是如果教得不好,把数学讲得干巴巴的,扼杀了好奇心,数学就难了。
陈省身(见【28】)
如果我们希望得到更多更好的社会支持,那么作为团体,我们必须做得更好。特别的,我们必须培养出更好的数学教师。我要非常谨慎地说,促使我决定成为职业数学家的最重要的人是 Lottie Wilson,她是我从前的高中数学教师。Wilson 夫人让人理解到她的课有一个本质的特征,她明白数学的崇高和神秘,她还知道,得到正确的答案无法用别的来代替。
P. A. Griffith(见【12】)
当然读者要问,是否必须要求学生学习正确的数学?要知道,不正确的数学是非理性的产品,不是从按部就班、有迹可循的思路得到的结果。我们不可能要求中小学生学习这种不合情理的数学。譬如说,要让学生掌握“负负得正”而不讲逻辑推理,唯一的办法就是说服学生某些数学只能死记硬背不能推理。一旦有了这个心理状态,学生难道还有希望去学习高深的数学吗?又譬如说,一般的课本要求学生了解“变量”是什么才能学习代数。在这种情况下,学生们不免产生一种错觉,每见一个符号就提心吊胆,以为这个符号一定是一个在纸上跳动的“变量”。这种数学是能够让学生学习的吗?
伍鸿熙
概述
近些年来,中小学的数学教育引起了世界各国的数学家的广泛关注,其中的代表者有:俄国的阿诺尔德(Arnold【2,3】),美国的巴斯(Bass【5,6】),匈牙利的罗瓦兹(Lovász【16】),中国的吴文俊(【26】)、姜伯驹(【14】)等。这里我们要介绍的是美籍华人伍鸿熙(Hung-Hsi Wu)关于中小学数学教育的理念与工作。
为了提高美国大、中、小学的数学教育水平,加州大学伯克利分校的知名数学教授伍鸿熙十年前正式转行投身数学教育,特别是为中小学数学教师做师资培训。伍教授的目标很明确,就是要让数学老师教好数学,最终让学生明白数学是能够学懂的。近十余年里,伍教授发表了多篇关于数学教育的文章,见诸数学教育的各种期刊杂志、会议文集。一些代表性的文章可见于伍鸿熙教授的个人主页,http://math.berkeley.edu/∼wu。
近二十年来,伍教授对中小学数学作了系统的剖析,融合师资培训的经验,将其成果总结成三套师资培训专著《数学家讲解小学数学》、《初中代数序曲》与《初中代数》、《高中数学教程 I-III》,分别适用于小学、初中、高中数学教师,真可谓“廿年辛苦不寻常”。下面我们就来简单地介绍一下这些专著。
《数学家讲解小学数学》(【19】)主要介绍了小学数学教师应该掌握的关于数的一些理论,包括自然数、分数、有理数、无理数以及涉及到的某些初等数论,分别详细地讨论了这些概念及其运算性质。在首都师范大学数学科学学院李庆忠教授的鼓励和丁洁、王盼盼、王丽芳等同学的帮助下,笔者已将《数学家讲解小学数学》翻译成中文,并由北京大学出版社出版。本文第三节将对此书展开详细的介绍与评述。
《初中代数序曲》(【20】)从分数讲到初等几何,目的是要把初中代数所需要的一切知识都说清楚。特别值得一提的是,书中对初等几何的讨论,开始尝试用直观的方法解释了“全等”与“相似”的基本概念,然后用同样直观的方法解释了两个三角形“相似”的刻划条件。这个处理初中几何的方法,是目前美国国家统一核心数学标准中从初二到高中的几何标准的基础。
《初中代数》(【20】)介绍初等代数的基本概念,包括正确运用符号、线性方程及其图形(为什么是一条直线)、函数的概念、一次与二次函数及其图形,等等。值得指出的是,这部分说明了,为什么懂得恰当地运用符号就可以明白“变量”是一个惯用的名词而不是一个数学上的概念。另一方面,这部分也指出了,为什么配方的技巧是了解二次函数所有问题的基本工具。
《高中数学教程 I-III》(【21】)内容涵盖了分数、负数、初等数论、代数(多项式、指数、对数、复数、代数基本定理)、几何(全等、相似、平面三角形的几何、圆的几何、面积与体积)以及初等的微积分。
2010 年 6 月,美国颁布了国家统一核心数学标准(Common Core State Mathematics Standard,以下简称 CCSMS),这也是伍教授自始至终参与完成的。
2011 年 9 月,伍教授在首都师范大学为数学院的师生做了题为“高观点下的中小学数学”的系列讲座,其间笔者有幸与伍教授近距离接触,从而对伍教授关于数学教育的想法和工作有了进一步的了解。这里笔者想谈谈我们的一点心得,与各位读者分享一下我们的点滴收获。本文旨在引起读者对伍教授所做工作的兴趣,最终目的则是希望引起教育同行们对数学教育的关注。
1 伍教授其人
伍鸿熙,1940 年出生于香港,1961 年在哥伦比亚大学取得数学学士学位,1963 年在麻省理工学院取得数学博士学位。他先后担任过麻省理工学院的研究员、普林斯顿高等研究院成员,1965-2009 年任教于加州大学伯克利分校,2009 年至今是该校名誉退休教授。1997-2005 年期间,伍教授与加州政府就数学教育进行了全方位的合作。
 伍鸿熙教授,图片来自 math.berkeley.edu
伍鸿熙教授,图片来自 math.berkeley.edu
2000-2001 年任美国国家教育进展评估数学指导委员会委员,2006-2008 年担任美国总统的国家数学顾问组的成员。他目前是 2011 数学与自然科学项目 TIMSS (Third International Mathematics and Science Study,第三次国际数学和科学评测)评审委员会成员。
伍鸿熙是知名的几何学家,是陈省身先生在伯克利所营建的几何王国的核心人物之一。他与学生 R. E. Greene 合作,对复流形的曲率与函数论关系作了精细的研究,得到了许多深刻的结果。受陈省身先生关于多复变函数的 Nevanlinna 理论几何化观点的影响,他在微分几何的框架下重新诠释并进一步发展了 Ahlfors-Weyl 关于全纯曲线的 Nevanlinna 理论,并形成专著《全纯函数的值分布论》,作为普林斯顿大学 Annals of Mathematics Study 丛书第 64 号出版。他还与萨克斯(R. K. Sachs)合作写了一本《广义相对论:给学数学的人》以及《广义相对论和宇宙学》,前一本书作为 GTM 丛书第 48 号出版,并且有萧欣忠先生的中译本(台北晓园出版社出版)。
在陈省身先生的带动与鼓舞下,伍教授多次回国讲学,其讲义经整理出版的有《黎曼几何引论》、《黎曼几何选讲》、《紧黎曼曲面引论》、《微分几何中的 Bochner 技巧》。这些著作脍炙人口、引人入胜,深受读者欢迎,培养了广大本科生和研究生对几何的兴趣,掀起了国内学习、研究几何的阵阵热潮,造就了一批又一批年轻的几何学者。
从 1992 年起,伍教授开始关注数学教育工作。他注意到,当时的中小学数学教育体系、教育方式以及教材中存在一系列问题。由于教师不能给予正确的指导,学生受不到正确的数学教育,以致逐渐丧失了学习数学的信心。作为数学家,他认为仅仅提出这些问题是远远不够的,关键是要想办法解决这些问题。如果仅仅指出问题而不提出解决问题的方法,那么隐含的意思就是这些问题很容易解决。但事实上,对于数学教育来说,我们必须重新思考数学知识方面存在的种种误区。如果数学家想致力于改进数学教育而不仅仅是想引发争论,那么他们就应该努力针对每个问题进行解决。正是这种想法促使伍教授逐渐转行走上了数学教育之路。
从 2000 年起,伍教授开始在美国组织一年一度的为期三周的中小学数学暑期师资培训,这一项目陆续受到了加州政府、洛杉矶教育办公室、Stephen D. Bechtel. Jr. 基金会的资助。这种师资培训以数学知识为主要载体,经受住了时间的考验,逐渐得到了大众的认可。十多年来,受到培训的教师的人数已成百上千,并且还将有更多的教师因此而受益。
2008 年,在从事数学教育近十年之后,伍教授在第四届世界华人数学家大会中学数学教育论坛上(见【18】)谈到了他的三点心得:
第一,数学教育是“数学工程”,与“数学”有异;
第二,数学家如要改善数学教育,需要作建设性的批评;
第三,数学家应该致力于师资培训。但要有收获,就需要对中小学数学有深切的认识。
2 伍教授谈中小学数学教育
存在的主要问题
伍教授认为,美国中小学数学教育的问题主要来自于三个方面:教师、教材和师资培训。同样的问题在大陆也相当严重,下面我们就分别来谈一谈这三个方面的问题。
2.1 教师方面的问题
伍教授认真思考美国中小学数学教育的问题根源所在,得出这样一个惊人的结论(见【29】):“在美国,中小学数学教育的最大问题是,很多中小学数学教师不懂数学。”伍教授举例说,有的数学教师甚至不明白定义和定理之间的差别。根据在三大洲(北美洲,亚洲和大洋洲)进行的教师培训的经验,他发现,这种情况其实很普遍。如果教师对他所讲授的学科缺乏很好的理解(见【23】),而妄图“以其昏昏使人昭昭”,那么后果可想而知,他根本不可能教好学生。反之,如果教师对所教的科目有透彻的了解,他本人的脑海中有一幅整体上清晰的图景,那么他教好这门课的可能性就大得多。举例来说,美国当代著名数学家格列菲斯(Griffiths)就是因为有幸遇到了这样一位出色的高中数学教师而对数学发生兴趣并最终走上了职业数学家的道路(见本文标题下的第二段引用),在另一个场合,他这样说道(见【8】的结尾部分):
在当今世界,科学知识尤为重要。许多工作都要求具备定量的、分析的技能。科学所教给你的事实就是实事求是(evidence- based reasoning)的精神,而我们正是在这一点上失败了。要成为本国的好公民,你需要对科学有一般的认识。
看看进化论的争辩、看看新闻和报纸上的种种资料,你会发现:事实上,对于进化论的大意以及如何理解新闻报纸上的资料,许多人连最模糊的观念都没有。造成这一问题的部分原因在于中小学的教学。教学体系的教师主要来自于教育院校。他们更多地停留在教学技能的层面而并没有深入到教育的本质部分。一个数学教师,哪怕是一个小学数学教师,都应该对这个科目有一个硕士水平的了解。唯有具备了如此深刻的了解,你才能用一种简单的方式更好地去教初等的内容。否则,你可能会弄得不必要地过分复杂。威尔逊(Wilson)夫人,我的第一个数学教师,绝对是一个富有天分的数学家,这一点使她成为一个伟大的教师。
格里菲斯是幸运的,但幸运往往只属于少数人。事实上,好的数学教师并不多见。让我们来看看世界著名的“杂交水稻之父”袁隆平的经历(见【27】):
我在学习方面喜欢凭兴趣,从小学到中学直到大学都是这样:对喜欢的功课,就特别注意听讲,还读这方面的参考书,成绩就很好;不喜欢的,就考 60 分,只求及格就行。我喜欢地理、外文,化学我也喜欢,我考试就拿高分。我最不喜欢数学,得 60 分就心满意足。记得当时学“负数乘以负数得正数”时,我很不理解,说正数乘以正数得到的是正数,这还好理解,为什么负数乘以负数也得正数?我就问老师为什么,老师不讲,只要我呆记。我不懂,那怎么呆记呢?要讲道理呀!从此我便对数学不感兴趣了。
可以想见,像袁隆平一样,绝大部分学生遇见这样的教师唯有“敢怒不敢言”(正如伍教授在做报告时所说的)。长此以往,学生不仅会泯灭对数学的兴趣,甚至会丧失对教师的信任。可以说,学生学不好数学,教师应负大部分的责任。再来看袁隆平的例子,事实上,不懂“负负得正”的中小学生何止他一个,最有趣的一个例子居然是后来成为大数学家的吴文俊先生,这也是袁隆平透露给我们的(见【27】):
记得有一件十分有趣的事,就是这次到北京,中央电视台对我和吴文俊先生做一个专访。这是我们两人头一次见面,但却是一见如故,相谈甚欢。……我说起小时候数学成绩不好,初中时向老师提问为什么“负负得正”,到现在还是没有弄清楚。吴老听后大笑起来。后来听说,原来他老先生在中学时对“负负得正”也是很不理解的。结果呢,他知难而进,成了大数学家。
由此可见,“负负得正”的问题绝非个人案例。事实上,《数学家讲解小学数学》第 29 章(这一章的标题就是负负得正)开篇的一句就是:“可以说,在中小学数学中,学生问得最多的问题就是负负得正的问题。”据笔者所知,这个问题不仅仅是学生的问题,也是许多中小学数学教师的问题:他们根本无法向学生解释清楚为什么“负负得正”。
2.2 教材方面的问题
伍教授指出的第二个问题是中小学数学教材中存在的各种问题:基本概念缺乏清晰的定义、数学推理论证含糊不清、数学符号的使用不恰当、内容设置缺乏整体的把握等。伍教授在【29】中说道,“中小学课本不及格,几乎完全不是数学。……美国的中小学课本几乎没有定义,2 除以 3 弄不清,分数学不了,数学的基本精神没有了。”同样的问题也暴露在大陆的中小学数学教材中。事实上,早在 1980 年代,著名数学家苏步青教授就曾指出合理编写中学教材的重要性,他在【17】中说道:
其次,要做好教材的编写工作。教材是进行教学的工具。……我把美国、德国、俄国、日本等国家的中学数学和理科课本翻阅了一遍,觉得有些地方值得借鉴。现在,我国中学数学和理科教材,比较重视基础知识和基本技能,注重启发学生的智力和培养学生的能力,这是好的。但是,有些内容陈旧,需要更新;有些内容浓缩、跳跃,如中学代数,把几何、三角混合编排;不少教师反映,按这样的顺序讲课不习惯。因此,编写教材也要广泛地征求中小学教师和科研部门专家的意见和建议,进行适当修改,编出一套比较理想的教材。
2.3 师资培训方面的问题
当然,对于教师和教材中出现的问题,我们不能简单地将责任全部推卸给教师与编者,而是要追究到他们所接受的教育上。伍教授指出(见【29】):“不论是职前的还是在职的对中小学教师的师资培训,到目前为止,常常文不对题,教师们学到的数学与他们教的数学离题万里。”如果教师自身所接受的培训不完善不合理、甚至带有根本性的错误,那么他们误人子弟就在所难免了。
首先,职前的师资培训,也就是大学里为师范生所开设的课程,通常只涉及高等数学,如微积分、线性代数、解析几何、抽象代数等等。这些课程讲解的都是正确的数学知识,具有完整的理论体系,强调精确的逻辑推理,有助于教师更深刻地理解数学。但是,未来的教师不仅要了解高等数学,更要学会给中小学生讲解他们听得懂的 (acceptable) 初等数学。我们仍用“负负得正”来说明。假定我们的出发点是分配律,那么“负负得正”就是其必然推论。伍教授在【22】的一篇附录中提到,在大学水平下,可以对所有的实数给出一个逻辑严密的证明:
我们首先来证明,对于任意实数 x 和 z 都有 $(−x)z =−(xz)$。注意到如果一个数 A 满足 $w + A = 0$,那么 $A = −w$。现在如果 $A = (−x)z$,由分配律意味着 $xz + A = xz + [(−x)z] =$$ (x + (−x))z = 0·z = 0$ 。所以,事实上有 $(−x)z = −(xz)$。对于给定的 $y$,如果我们令 $z = −y$,这就推出 $(−x)(−y) = −(x(−y))$。
现在设 $B = (−x)(−y)$,要证明 $B = xy$,只需要证明 $xy − B = 0$。这是对的,因为 $xy − B = xy − [−(x(−y))] =$$ xy + x(−y) = x[y + (−y)] = x·0 = 0$。这就是我们要证明的。
这个证明无懈可击,但是却因为太抽象了而难以为中小学生所理解。作为比较,读者可以在本文第 3 节找到负负得正的一个初等证明。
再如,两个分数 $\frac ab$ 和 $\frac cd$ 的乘法是 $\frac{a}{b} \times \frac{c}{d}=\frac{a c}{b d}$。从抽象代数的立场来看,这个公式完全是一个定义。这个公式使得我们可以在一个整环的分式域上引进乘法结构,确定了 $\frac ab$ 和 $\frac cd$ 的乘积为 $\frac{ac}{bd}$。但是,如果从中小学的眼光来看,这个公式则是一个大定理。因为中小学生根本不知道什么是整环,什么是其分式域。他们只懂得两个整数相乘的含义(例如 $12 \times 27=\underbrace{27+\cdots+27}_{12}$)。所以我们要从这个出发点去定义两个分数的乘积。然后再用这个定义去证明乘积公式 $\frac{a}{b} \times \frac{c}{d}=\frac{a c}{b d}$。这是一个太平凡的证明!所以,如果在中小学数学中我们说 $\frac{a}{b} \times \frac{c}{d}=\frac{a c}{b d}$ 是一个定义,那就大错特错了。这就是不正确的数学的一个典型例子。
由上面两个例子可以看出,“正确的中小学数学”与“正确的抽象数学”可能有天壤之别。目前在讨论中小学数学时,许多师范类专业学生对“数学正确性”的了解,还只停留在“正确的抽象数学”的阶段,而对“正确的中小学数学”一无所知。所以,大学里的师范类数学专业需要设置专门的针对性课程,帮助未来的教师更好地讲授初等数学。对此,他打了一个巧妙的比方:拉丁语是法语的起源语言,而且比法语更复杂。那么为了造就一名好的小学法语教师,难道让他们只学习拉丁语就够了吗?
此外,大学的数学师范类课程中通常也开设了一些由教育学方面的教师讲授的教学方法类的课程。伍教授认为,这些教育理论确实有必要学习,但更好的办法应该是,把要教的正确的数学知识融入到这些理论框架中去。这就要求,数学界与教育学界一起合作共同设置合理的课程,确保未来的数学教师既对数学有深刻的理解,又能懂得如何正确地讲授中小学数学。
其次,在职教师的师资培训也是一项巨大的工程。多年来,数学师资培训里充斥了复杂的教育理论、课堂教学策略、教具使用、教学效果评估等等。这些对于教学固然重要,但最重要的还应当是所讲授的知识本身:要确保教的是正确的数学。许多在职的数学教师多年积累下来的教学经验大多是基于不合理的数学(参见本文标题下第三段引言),所以,更有价值的师资培训应当以正确的数学知识为主要内容。(未完待续)
 左起:伍鸿熙教授、林开亮、赵洁、王盼盼(由伍鸿熙夫人 Kuniko 摄于首师大数学院)
左起:伍鸿熙教授、林开亮、赵洁、王盼盼(由伍鸿熙夫人 Kuniko 摄于首师大数学院)
3《数学家讲解小学数学》简介
3.1 总论
总的来说,伍教授的这些著作都是针对 “正确的中小学数学” 而写的。就是说,这些书是根据从小学到高中的数学课程而写的。所以书中的一切概念和推理,都是可以适用于中小学课堂的正确的数学(而不是为了追求严格性而写的数学)。伍教授之所以非常强调正确的数学,是因为他发现,目前公众对中小学数学的误解恰恰在于,他们认为学校讲授的数学基本上是正确的。但事实上,如果去翻看中小学数学教材,就立即看见错误百出。所以,当务之急就是要更正这些错误,确保所讲授的数学是正确的。本着这一宗旨,《数学家讲解小学数学》的致读者部分这样结尾:
我希望你们已经开始发现,阅读这本书需要下大力气,这样才能保证学到并讲授正确的数学。正确的数学比不正确的要好教,正如一篇好文章比一篇差文章要容易读。你所下的功夫最终将有助于你成为一个更出色的数学教师。这便是本书要讲的全部内容。
谈到伍教授的这些著作,笔者忍不住想要将它们与 20 世纪最有影响的两个数学教育家克莱因(F. Klein,1849-1925)的著作《高观点下的初等数学》(【15】)和弗兰登塔尔(H.Freudenthal,1905-1990)的著作《作为教育任务的数学》(【11】)做一个比较。先来看弗兰登塔尔《作为教育任务的数学》。正如作者在序言(见【11,第 4 页】)中所说的,“本书虽然也研究了许多细节,但它首先绝对是一本数学教育哲学的书。” 他在书中研究了哪些课题是可以教的,提纲挈领地论述了中小学数学的一些基本课题,强调要将近代数学的某些思想渗透到中小学数学中去。可以发现,伍教授《数学家讲解小学数学》与之形成鲜明的对比:《作为教育任务的数学》是构建抽象理论框架,宏观概括地指出问题,谈的是一种理想和目标;而《数学家讲解小学数学》则是论述具体的基本数学知识,直面学生可能遇到的各种问题并一一化解,处理的是现实和实践。我们举一个例子以说明《作为教育任务的数学》的风格(见【11】):
乘法的矩形模型关于两个因子是对称的,但是当具体的数量相乘时就失去了对称性:如果件数乘以单价、工作时数乘以小时工资,月数乘以 30,那么在乘数与被乘数之间或多或少地存在着明显的区别。
教学法专家在除法中觉察到了这个不对称性,由于除法是一种高度直观的运算,所以 “5 个人分 20 块面包,每人分多少?” 与“20 块面包,每个人分 4 块,可以分给多少人?”从直观上来看,这两个问题就是截然不同的事情。前者 20 块面包由 5 个人分称为分配除法,后者 20 块面包除以 4 块面包是比的除法。这就要求学生用不同的方法解两个问题,特别是,两种情况下的长除法是不同的。……我也认为,应该训练学生解两类问题,例如,“4 乘以什么数等于 20?”与 “什么数乘以 4 等于 20?” 等等。但是,不要在每一种情况下得出一个特殊的法则,而应理解为它们具有共同的模型,所以一种法则就足够了。我之所以提出这个问题,就是因为,如果某些教学法专家不是从量的基础理论出发来考虑除法,那么除法的两重问题就会一代一代地死灰复燃。
弗兰登塔尔这里所说的 “除法的两重问题” 在《数学家讲解小学数学》§7.1 中有详细的讨论,分别被称为等分除解释和包含除解释。伍教授进一步指出,除法的这两种解释相互对偶,因为乘法满足交换律。
再来看克莱因的《高观点下的初等数学》,伍教授在首都师范大学所做报告的大标题是 “高观点下的中小学数学”,看似与此非常相像,实则大相径庭。吴大任先生曾经为中译本写了专门的介绍(见【24】),对这三卷书赞誉极高。这一点不容否认:一个中小学数学教师如果能把这三卷书读下来,那么他的修养必定可以得到极大的提高。但是,应该坦白承认,这三卷书其实并不适合教师直接应用于中小学数学课堂。因为该书要求读者事先掌握了初等数学,然后再进一步拔高,这就是克莱因所谓的 “高观点下的初等数学”。事实上,这一点早就被弗兰登塔尔指出过了,他在【11】如是说:
有许多初等数学的现象只有在非初等的理论框架下才能深刻地理解。克莱因的观点就是想为教师日常的课堂活动提供一个科学的背景。但是,克莱因在《高观点下的初等数学》中提供的背景对中学教师而言,只能作为周末的风景观赏,却不能作为间接的手段进入课堂。因此,不能影响中学数学。例如,克莱因详细说明了伽罗瓦理论是中学求解二次方程、三次方程的背景,但是,事实上伽罗瓦理论高踞于中学数学水平之上。
因此,克莱因《高观点下的初等数学》对中小学数学教师的教学过程并不能有直接的帮助。相比之下,伍教授的这套师资培训教材则是直接论述教材中的基本知识,直面学生有可能遇到的理解上的困难和疑惑,所以对改进中小学的数学教学会有立竿见影的效果。
3.2《数学家讲解小学数学》的基本特色
根据笔者的体会和理解,总结起来,《数学家讲解小学数学》一书至少有以下十点基本特色:
一、等级森严:循序渐进。
这本书是写给中小学数学教师的,但基本上是从零开始,除了要求读者对基本的加减乘除四则运算有所了解以外,不需要任何其他的准备知识,所以即便是对一般的读者(特别地,包括学生家长)来说,读这本书也应该是毫无困难的。正是因为这本书没有对读者做过多的要求,所以在材料的选择和内容的安排上,先后次序非常有讲究。本书的主题是数,内容上分为五个部分,依次分别是:自然数、分数、有理数、初等数论、小数。除了初等数论以外,这些课题都是中小学数学中的常规内容(对于初等数论,我们将在下面第六款中讨论)。这一安排不仅遵循了各个课题之间内在的等级结构,而且符合中小学生学习数学的循序渐进的规律。
二、语言清晰:定义精确。
学习数学最重要的一点就是学会逻辑推理,而定义是进行逻辑推理的基础。数学中所讨论的对象都应当非常清晰、具体,否则容易给往后的逻辑推理造成不必要的麻烦。本书最大的特色之一是,对所有论及的基本概念都给出了精确的定义。例如,数、分数、小数、有理数以及数的四则运算等基本概念甚至四舍五入的概念在本书中都能找到清晰的定义。举例来说,分数的乘法在书中定义为:
$\frac{m}{n} \times \frac{k}{l}=$ 边长为 $\frac m n$ 和 $\frac kl$ 的矩形的面积。
再如,书中将有限小数定义为一类特殊的分数:
有一类分数比较特别,值得在一开始就单独指出来,即分母是 10 的某个正整数次幂的分数,如:
$$ \frac{1489}{100}, \quad \frac{24}{100000}, \quad \frac{58900}{10000} $$这些分数被称为 “十进制分数”。不过,使用另一种记法和称谓可能更容易理解。1593 年,德国传教士、天文学家克拉维乌斯明指出,如果我们舍弃分数的形式,一个十进制分数可以更容易地以如下方法写出:只写出分子,并用所谓的小数点记录分母中有多少个 0(上述十进制分数中第一个有 2 个 0,第二个有 5 个 0,第三个有 4 个 0),于是上述分数相应地改写为:
$$ 14.89, \quad 0.00024, \quad 5.8900, $$用这种小数点的方式写成的数称为有限十进制小数或有穷十进制小数。
作者进一步强调了这一定义的合理性:
就学习数学而言,本书中小数的这一定义可能给读者造成第一个严峻的障碍。我们来重复阐述一下主要内容:一个小数,例如 0.0938,它本身的意义是一个分数,即
$$ \frac{938}{10^{4}} $$你可能会将小数的这一特殊 “解释” 认为是开玩笑,对此不加以太多的注意,然后接下来就全部忘记。然而,小数这一定义的作用正是在于要求你重新思考已学过的小数的知识,并以此定义作为出发点重新整理所学的知识,来对已有知识作一个整体的新的评价。这可并非一件容易的事情,因为你已经习惯于认为 5.89 表示 5 个 1,8 个 $\frac 1{10}$ ,9 个 $\frac{1}{100}$ 之和,并不考虑它是什么意思,也不考虑这样定义会在将来用小数计算时给你带来多大麻烦。我们也深深理解,要接受一个全新的定义需要下很大的功夫,(其难度无异于学习一门新的语言),我们也会在后续的章节中尽最大可能帮助你理解。不过仍然需要你自己努力,因为如果不亲自动手,小数部分的知识对于你来说将永远很难对付。
还有一个例子特别值得在这里一提,这就是第 18 章引入的匀速运动的定义。伍教授注意到,在中小学数学文献中,人们很难找到匀速直线运动的准确定义,于是几乎所有与运动有关的问题都要么是通过单位变化率来做,要么是通过比例推理来做,而不是数学推理。他写道,如果在要求学生求解运动问题之前却没有预先告诉他们需要知道哪些条件,那么这绝对不会是成功的教育。
有鉴于此,伍教授在本书中第 18 章第 293 页对匀速运动给出了一个精确的定义:
若一个物体在任意的时间段 $t$ 内的平均速度 $d$ 都等于某个固定的 $\frac dt$,则称这个物体做的是匀速运动。
此外,对于读者可能不明白的较为陌生的一般观念,书中常常以脚注的形式加以解释。“在数学中,引理也是一个定理,但是人们对它的兴趣略逊一筹,它的特点是,通常带有一定的技巧性,但可能不是作者要写的最本质的东西。”
笔者之前曾经见过法国当代著名数学家塞尔(Serre)曾在【8】对引理作出如下诠释:
我应该解释一下引理是什么吗?登山者从一级上到更高的一级需要支撑,引理就是数学家的支撑。
为此,笔者曾向伍教授建议在中译本中添加一个译者注作为补充,引用塞尔先生的上述绝妙比喻,伍教授欣然采纳了这一建议,并且一再对译者授权说,凡是有助于读者理解的提议,都可以大胆采用。
三、逻辑严密:推理论证井井有条。
该书对中小学数学中的诸多基本事实都给出了清晰明了的证明,这些证明往往都是从定义出发,一步一步、环环相扣地推导,每一步都有理可循,而且言简意赅、要言不烦。
作为例子,我们来看第 13 章对于等值分数定理的证明。
给定分数 $\frac mn$,我们要证明,对于任意非零自然数 $c$,有 $\frac{m}{n}=\frac{c m}{c n}$。我们知道,$\frac{m}{n}$ 表示 $m$ 份 $\frac{1}{n}$,下面证明它也表示 $cm$ 份 $\frac{1}{n}$。在数在线,首先考虑 $\frac{1}{n}$ 的所有倍数,接着考虑 $\frac{1}{n}$ 的所有倍数,把 $\frac{}{cn}$ 的每两个相邻倍数之间的线段称为小线段。
则对于 $\frac{1}{n}$ 的任意两个相邻倍数之间的线段来说,小线段把它分成 $c$ 个相等的线段。此时,观察到,$\frac{1}{n}$ 的任意两个相邻倍数 $\frac{1}{n}$ 之间的线段长度为 $1$,每个小线段的长度为 $\frac{1}{cn}$。而前者恰为由 $c$ 个小线段拼接而成,所以 $\frac{1}{n}$ 表示 $c$ 份 $\frac{1}{cn}$。由于 $\frac{m}{n}$ 表示 $m$ 份 $\frac{1}{n}$ ,$\frac{1}{n}$ 表示 $c$ 份 $\frac{1}{cn}$ ,所以 $\frac{m}{n}$ 表示 $cm$ 份 $\frac{1}{cn}$ ,而 $\frac{cm}{cn}$ 也表示 $cm$ 份 $\frac{1}{cn}$ ,这样我们就证明了 $\frac{m}{n}=\frac{c m}{c n}$。这就证明了等值分数定理。
书中还有很多这样的例子,第 17 章对分数的乘积公式的证明,第 27 章对 “去括号” 法则的证明等等,也都是从精确的定义出发。再如,对匀速运动问题的求解都是基于匀速运动的定义。
四、由简到繁:从特殊到一般。
书中的论述和证明常常遵循这样一个模式:先讨论一个特例,揭示其关键点所在,然后将特殊情形下的论证推广到一般情况。例如,书中对” 负负得正” 的证明,先考虑一个重要的特殊情况 $(-1)(-1)=1$,然后过渡到对所有的正整数 $m$, $n$ 来证明 $(-m)(-n)=mn$,最后才对任意的有理数 $x$, $y$ 证明 $(-x)(-y)=xy$(负负得正)。下面我们依次援引【19】给出的证明。
首先来看最特殊情况下的负负得正:$(-1)(-1) =1$。
定理 $(-1)(-1) = 1$。
证明:令 $z = (-1)(-1)$。我们的目标是证明 $z = 1$。首先想想:对于有理数 z,如何证明它是否等于 $1$?可以尝试的一种方法是,验证 z 是否满足 $(-1) + z = 0$。如果是,则 $\vec{z}$ 是方向向右长度为 $1$ 的向量,如下图所示是从以 $-1$ 为起点 $0$ 为终点,因此有 $z=1$。
通过计算有
$$(-1)+z=1 \cdot(-1)+(-1) \cdot(-1)$${根据 (M2) 以及 $z$ 的定义}
$$=(1+(-1)) \cdot(-1)\quad\text{(分配律)}$$$$=0\cdot (-1)$$ $$=0\quad\text{(根据 M3)}$$所以可得 $z=1$,也就是 $(-1)(-1)=1$。证毕。
注:这里的 (M2),(M3) 是对有理数的乘法所作的三条基本假设的第二条和第三条,分别是:(M2)如果 x 是任意的有理数,那么 $1 · x = x$;(M3)对任意有理数 $x$ 有 $0 · x = x · 0 = 0$。接下来我们再来看正整数情况下的负负得正:$(-m)(-n) = mn$。$(-m)(-n) = mn$ 在一般情况的证明与前面的特殊情况本质上是一样的。
我们首先证明,对任意的正整数 $n$ 有
$(-1)(-n) = n.\tag{*}$
根据 “去括号” 法则,
$$ -n=-\underbrace{(1+\cdots+1)}_{n}=\underbrace{(-1)+\cdots+(-1)}_{n} $$因此
$$ \begin{aligned} &(-1)(-n)=(-1)(\underbrace{(-1)+\cdots+(-1)}_{n})\\ &=\underbrace{(-1)(-1)+\cdots+(-1)(-1)}_{n}\quad\text{(根据分配律)}\\ &=\underbrace{1+\cdots+1}_{n}\quad\text{(根据定理)}\\ &=n \end{aligned} $$这就是我们要证明的。因此,对任意的正整数 $m, n$ 有
$$ \begin{aligned} &(-m)(-n)=(\underbrace{(-1)+\cdots(-1)}_{m})(-n)\quad\text{(根据 “去括号” 法则)}\\ &=\underbrace{(-1)(-n)+\cdots+(-1)(-n)}_{m}\quad\text{(根据分配律)}\\ &=\underbrace{n+\cdots+n}_{m}\quad\text{(根据 (∗))}\\ &=m n \end{aligned} $$
对于 $m, n$ 是任意有理数的情形,留给有兴趣的读者,可参见【19】。
五、评论中肯:示人以朴。
本书中穿插着许多注记。这些注记往往是小结性的,通常一针见血地指明问题的关键所在。比方说,对于某些结果,书中给出了不止一个证明,有的是计算性的,有的是概念性的,伍教授在注记中对各个证明做了比较和点评,评语切中肯綮,使人读了眼前一亮,仿佛若有光。
例如,大概很少有人思考这一问题:为什么长除法(最后可以得出(除法的)商和余数,伍教授在书中一个具体举例之后点评到:“长除法通过把原来的除法分解成一系列简单的带余除法,使得人们可以简单地甚至是机械地求出商和余数。” 这就点明了长除法的实质!
又如,在第 27 章从定义出发直接证明了 “去括号” 法则以后,我们可以读到以下
注记:学生推导 “去括号” 法则的通常方法是“乘以 $-1$ 并应用分配律”,亦即,
$$ \begin{aligned} &-(x+y)\\ &=(-1)(x+y)\\ &=(-1) x+(-1) y\\ &=-x+(-y)\\ &=-x-y \end{aligned} $$这个计算是正确的,但是对于 “去括号” 法则的证明来说却显得有些繁琐。上述计算应用了下述事实,即,对于所有的有理数 $x$ 有 $(-1)x =-x$。这是关于有理数乘法的一个事实,要在讲有理数的乘法时才能证明。然而,对“去括号” 法则的一个概念上的理解需要认识到,它们仅仅与有理数的加法和减法有关,而与乘法无关。因此,“去括号”法则的一个更直接的证明是很有价值的。
这个注记表明,“去括号” 法则的实质并非我们通常误以为的 “乘以 $-1$ 并应用分配律”,而是最基本的有理数加减法(乘法的概念是不需要的)。
古人云:良工不示人以朴。(本意是,好的木匠不把未加工好的东西给人看。比喻有贤德的人一定要把人培养成材或所做的事一定要完美。朴:没有细加工的木材。)近代著名数学家许宝騄(1910–1970)则推崇在教学上要做到 “良工示人以朴”,他的意思是,要把原始的、真实的思想讲解给学生,而在形式上、在证明方法上要力求简明扼要而无冗言赘文。简而言之,就是以朴素的方式说清楚本质。按照这一说法,伍教授确实做到了 “示人以朴”。
六、内容新颖:中小学数学基本假设和初等数论的引入。
伍教授还注意到,在中小学数学中,有一个基本假设不可或缺,这就是他所命名的中小学数学基本假设。这是他对中小学数学教材的一个重大贡献,他在《数学家讲解小学数学》中用了整整一章(第 21 章)的篇幅讨论这个假设。
中小学数学有意避开讨论无理数,但却试图假装处理了包括有理数和无理数在内的所有实数,这一事实直到 2001 年的文献中似乎还没有明确说清楚。
从普通的教科书中可以推断出,这些教材隐含地要求学生掌握下面的假设,我们建议称作中小学数学基本假设:分数的所有代数运算的结论都可以推广到全体实数。
这是一个洞察很深刻的假设。它允许学生像处理分数一样处理无理数,即使不知道无理数是什么。因此有的学生不经思考就能够写出下面一类典型的式子:
$$ \sqrt{2}(\sqrt{3}+\pi)=\sqrt{2} \sqrt{3}+\sqrt{2} \pi $$或
$$ 37 \times \pi=\pi \times 37. $$他们仍然会用分配律证明第一个式子,用交换律证明第二个式子。尽管每条定律或等式我们都只在分数的情形下进行了证明。换句话说,中小学数学基本假设潜在地发挥著作用。
此外,伍教授还用整整一个部分(第四部分)介绍了初等数论的基本内容。正如前面已经提到的,相对于其他部分而言,初等数论这一部分是本书选材上的
最大突破。伍教授认为,中小学的数学教师必须了解一些数论,特别是以下两点:
第一:一些较小的整数的整除性规律。例如,为什么判断一个整数能否被 3 整除只需要看它的各位数字之和能否被 3 整除。然而,只要讨论整除性,就不得不提到质数以及它们的简单性质,就需要了解初等数论。
第二:为什么分数可以化简为最简分数,以及哪些分数可以化为有限小数。这两个问题的回答分别由以下两个定理给出(见【19】)。
定理 每一个分数 $\frac{m}{n}$ 可以通过约去分子和分母的最大公因子得到最简分数。而且其最简分数在下述意义下是唯一的,如果 $\frac{a}{b}=\frac{A}{B}$ ,其中 $\frac{a}{b}$ 和 $\frac{A}{B}$ 都是最简分数,那么 $a = A$ 且 $b = B$。
定理 一个最简分数 $\frac{a}{b}$ 可以化为一个有限小数的充分必要条件是分母 $b$ 具有形式 $b=2^{s} 5^{t}$,这里 $s$ 和 $t$ 是自然数。
但是,如果不知道欧几里得算法和算术基本定理,就无法证明上述两个定理。伍教授一再强调,虽然学生可能没有足够的时间学习这么多的数论知识,但是,每一位中小学数学教师都应该学会如何使用欧几里得算法和算术基本定理,并且要了解其证明。
有一点值得在此特别指出,初等数论中的许多基本事实都可以从欧几里得算法得到,而欧几里得算法的实质则是一连串的带余除法(在这一点上,与长除法极为相似)。因此可以认为,初等数论的很多结果是带余除法的自然延伸。事实上,伍教授在介绍第四部分时这样说:本书的这一部分或许可以视为 “对带余除法中余数的重要性的一个反思”。因此,对于那些从来不曾接触初等数论的读者来说,读到这一句就好比吃了一颗定心丸:打开这一秘门的钥匙,其实是我们所熟悉的带余除法。
七、误区分析与教学评论。
伍教授在书中指出:
作为老师,你不仅仅要认识到什么是对的,更重要的是要认识到什么是错的,这样才能给予学生正确的指导。
书中对于中小学数学中师生的常见误区作了深入的分析,这是本书的一大亮点,对教学具有极为重要的价值。例如,第 18 章用一节的篇幅探讨了分数除法的教学中的几种错误观点。
此外,书中还穿插有多处教学评论,例如第 39 章复习有限小数时我们可以读到以下
教学评论 按定义,一个有限小数是一个以 $10^n$ 为分母的分数。这一事实不论如何强调都不会过分。事实上,中小学教材中最常见的一个败笔就是对有限小数缺乏一个清晰的定义。
评论结束
八、注重历史:回顾与前瞻并重。
伍教授在书中对历史上许多著名的成就和问题都有简要的介绍,比如说,埃拉托色尼筛法、毕达哥拉斯三元数组、欧几里得算法和哥德巴赫猜想等等,甚至对数的乘法以及单位 “米” 的历史演化也有简单的介绍。同时,对某些古老问题的近代进展也有提及,例如,维格纳朵夫 (I. M. Vinogradov) 和陈景润各自对哥德巴赫猜想所作的贡献,甚至提到了陶哲轩 (Terence Tao) 与格林(B. Green) 2004 年关于质数分布的工作。这让我们回想起数学家塞尔的建议(见【7】):
要让学生明白,数学是活生生的,而不是僵死的(学生有这样一种倾向,认为只有在物理学或生物学中才有未解决的问题)。讲授数学的传统方法有一个缺陷,就是教师从来不提这类未解决的问题。例如,数论中就有许多诸如此类的问题,十几岁的孩子就能很好地理解它们。这当然包括费尔马大定理(塞尔说这话的时候它还没有被证明),哥德巴赫猜想,以及关于存在无穷多个形如 $$ 的质数的猜想。教师也可以随意介绍一些定理而不加证明,例如关于非平凡算术级数中存在无穷多个质数的狄利克雷定理。
无独有偶,陈省身先生在【28】中所表达的看法(见本文标题下的引言)与塞尔的上述观点遥相暗合、有如共鸣,值得引起我们活跃在一线的中小学数学教师特别注意。
伍教授在书中也介绍了中国古代数学的一些伟大成就,例如,第一章记数法中就介绍了源于古代中国的十进制位值制。伍教授甚至认为,十进制或许是中国对世界数学的最大贡献。第一次听到这个说法的人或许会觉得不可思议。事实上,我们可以在精通中国古代数学史的著名数学家吴文俊那里找到更为肯定的说法(见【13】):
进行算术运算,首先要有一个可以表示出任意大的整数的方法。在中国古代,就为此而创立了完整的 10 进位位值制。世界古代各个名族,都有不同形式不同程度的进位制记数法,如巴比伦的 60 进位制,埃及与希腊的 10 进位制以及中美与南美玛雅民族的 20 进位制等。但是他们的进位制有时是不完全的,更谈不上位值制。至于印度,至少在 6 世纪以前,其以位值制的记数法,还没有发现过。
……位值制的数字表示方法极其简单,因此也掩盖了它的伟大功绩。它的重要作用与重要意义非但为一般人所不了解,甚至众多数学家对它的重要性也熟视无睹。而法国的数学家拉普拉斯则独具慧眼,提出位值制应在一切有用的发明中列于首位。中国民族是这一发明当之无愧的发明者。中华民族应以创造出这一发明而引以自豪。
吴文俊先生下面的一段话(见【25】)完全肯定了中国古代数学文明对当代中小学数学的贡献:
中小学数学中的算术、代数这些部分,从记数以至解联立线性方程与二次方程,实质上都是中国古代数学家的发明创造,早就见之于中国的《九章算术》甚至是更早的《周髀算经》等书。根据钱宝琮考证,《九章算术》完成于公元 50-100 年间。但除个别片段以外,基本内容应该完成于公元前 200 年或者更早一些(这是某些西方数学史家的意见。有的甚至提到公元前 1000 年,
例如 Scott 的著作《数学史》,1958 年)。根据钱宝琮考证,另一部《周髀算经》成书于公元前 100 年左右。
根据这一说法,中小学数学的大部分内容都可以在中国古代找到源头,因此,在我们的中小学课堂上,应该尽可能地将这些中国古代数学成就融入进来。正如著名的数学史专家、数学史名著《古今数学思想》的作者克莱因 (M. Klein) 在接受访问时一再强调的(见【1】):
中学和大学里的每一位数学教师都应了解数学史。理由很多,但是最重要的一个原因或许是,数学史乃是指导教育的指南。
……历史可以在教学中扮演重要的角色。例如,如果告诉初学微积分的学生们:尽管牛顿和莱布尼兹是名声显赫的前辈,但是他们自己也没有能够透彻地理解微积分的许多概念,数学家们经过了大约 200 多年的努力,才把这些概念搞清楚;那么当学生们开始时不能很好地理解这些概念,也就不至于感到迷惘。相反的,他们将得到鼓舞而继续学下去。历史还有许多其它的教育价值。
在我们的情形而言,如果中小学生能够了解到,课本上种种美妙的数学(勾股定理、辗转相除法、以至于中国剩余定理)竟是从几千年之前的老祖宗传承下来的,那么他对数学的兴趣和信心一定大增。
九、记号恰当、排版美观。
所有的记号都经过了精心的选择。书中凡是用代数运算式定义的概念,都使用了符号 $=$,而且所定义的概念用黑体标出。例如,第 27 章对有理数的减法定义如下:
$$ x-y \stackrel{\text{定义}}{=} x+y^{*} $$
又如,为了显示出带余除法中商与余数,本书采取了加方框标记的方法,例如 $25$ 除以 $6$ 的带余除法表达为
$$ 25=(\fbox{4} \times 6 )+\fbox{1} $$这一记号比通常出现在美国中小学教材的记号(见下文)优越多了。对此,伍教授说道:
在中小学数学里,$25$ 与 $6$ 作带余除法,所得商为 $4$ 余数为 $1$,通常写作
$$ 25 \div 6=4~\mathrm{R}~1 $$应当把这种记号剔除出所有的教科书,有很多原因,其中一条是,它没有任何意义。从最基本的角度看,如果允许写 $25÷6=4R1$,那么我们也不得不写出 $21÷5=4R1$,因此,$25÷6=21÷5$,因为它们都等于 $4R1$。可是,“四组物体,每组 $5$个,还余 $1$个”与“四组物体,每组 $6$ 个,还余 $1$ 个”,怎么能一样呢?此外,我们还可以通过理解等号的意思来更深入地讨论 $4~R~1$ 的意思。我们已经把两个自然数相等定义为数在线的对应点重合,但是 $25÷6$ 和 $4~R~1$,哪个都不是自然数,所以它们之间的等号只是在拙劣地挪用记号。即使我们承认一般的分数和实数(见第二部分,特别是第 12 章和第 21 章),等式 $25÷6 = 4~R~1$ 仍然不具有任何意义,因为 $4~R~1$ 不代表任何数。带余除法的正确的表示方式是 “$25 = (4 × 6) + 1$”,
这才是教师真正应该带到课堂上的东西。
全书采用功能强大的 $\TeX$ 软件排版,数学公式非常美观。第一次出现的数学名词以及相应的记号,作者以黑体标出;运算法则、方法或者是结论类型的段落,缩进成段以示强调。特别是,某些证明经过作者的精心排版之后变得一目了然(例如第四款所举的 “负负得正” 的证明之排版),这样的排版可以作为课堂板书之规范。
十、举例典型、习题丰富。
该书的一个重要特点是,选取了大量具体的典型实例来左证其观点。比如,在第 23 章一些有趣的应用题中,伍教授引用了俄国的两道题目作为例题:
问题 新鲜的黄瓜中,全部重量的 99% 都是水分。现将 300 磅黄瓜置于储藏室里,但是等拿到市场卖的时候,人们发现水分的重量只剩下了 98%,请问水分挥发之后的这些黄瓜重量是多少?
问题 有一瓶红酒和一壶茶水,先从茶水中盛一勺倒入红酒中,均匀搅拌后再盛一勺倒回茶水中。请问此时瓶中含有的茶水和壶中含有的红酒,哪个更多?如果没有搅拌均匀,情况又会怎样?
这两道题目出现在第 22 章比例和比率之后,因为它们既可以用分数的比例方法做,又可以用常识解释,从而可以让学生对如何正确使用比例计算有很好的理解。
古人云:“纸上得来终觉浅,绝知此事要躬行。” 解题可以认为是一个实践活动,以衡量读者是否掌握了所学理论。伍教授在每章后面都精心安排了许多基础而新颖的习题,对正文是一个很好的补充。此外,全书中穿插了许多动动手,这些都是基础而简单的练习,可用于随堂检测与巩固。
4《数学家讲解小学数学》对中小学教学的指导意义
《数学家讲解小学数学》是一本典型的侧重正确知识性的师资培训教材,旨在对教师的知识理论结构进行一次彻头彻尾的整理。当然,师资培训教材不能作为学生课本直接搬进课堂,还需要学生课本的编写者以讲授正确的数学知识为基本原则,以中小学生的认知特点为指导,编写出循序渐进的、适合中小学生使用的课本。教师在掌握了正确的数学知识后,也应当辅以适合学生认知的教学策略,以便于学生更好地理解数学。
为了解释这一点,我们以三年级阶段学生对分数的初步认识为例,介绍该书对中小学教学的指导意义。
伍教授强调,每一个数学课题的教学都必须是阶梯式地缓慢递进的过程。例如,在他参与制定的 CCSMS 中,分数的教学从三年级贯穿到七年级。其中,三年级阶段的分数教学的目的有三:
一、理解分数 $\frac 1b$ 表示把一个整体平均分成 $b$ 个相等的部分后其中 $1$ 个部分的大小,分数 $\frac ab$ 表示把一个整体平均分成 $b$ 个相等的部分后其中 $a$ 个部分的大小。
二、理解分数是数在线的一个点;把分数表示为数在线的一个点。
三、解释等值分数的意义,比较分数的大小。
在三年级,学生首次接触分数的部分、整体关系,鉴于学生对数学的认知程度较浅,所以只能用简单的比喻和直观的推理给学生展示分数。但即使是在这个探索和体验的初步阶段,教师仍然可以选择好的方法进行分数的教学。至少,教师可以帮助学生养成习惯:在讨论分数时要注意选择某个固定的整体作为单位 “1”,而且要尽量精确。在众多表示分数的形式中,正方形和数线这两个数学图形脱颖而出,因为它们表示的不是物体的“形状”,而是物体的“度量”,即面积和长度。例如,把单位正方形任意分割成面积相等的部分,那么 $\frac 14$ 可以表示其中一部分的面积。如图所示:
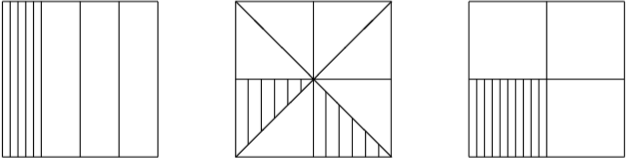
这样对正方形进行多种分割,直观又形象,但也暗示学生,这种平均分割针对的是面积而不是形状。对于规定好的单位正方形,分割后所得形状不同的部分也有可能表示同一个分数。
再如,教师不应该唐突地提出如下问题:“下图阴影部分表示的分数是多少?”
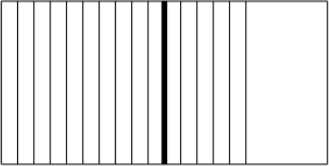
这个问题的不合理性在于没有明确地指出单位 “1” 是什么。如果单位 “1” 是整个矩形的面积,那么阴影部分的面积应该是 $\frac 34$ ,如果单位 “1” 是单位正方形的面积,那么阴影部分的面积就是 $\frac 32$。因此,最好养成习惯,从一开始就强调单位的重要性,以避免这种歧义。
伍教授认为,如果把分数想象成某些图形对学生的学习有帮助,那么当然可以尽情地使用这些图形,例如馅饼、苹果、正方形、或一些圆圈等。教师可以用一切可以想到的图标为学生展示分数,但是一定要保证使用语言的准确性,明确单位 “1” 代表的是图形的度量而不是图形的形状,并在同一个题目中保证单位 “1” 的大小保持不变。
当学生对分数有了以上初步的认识后,就可以逐渐体会其精确的数学定义,逐步清晰地理解分数是数在线的一个点,并把分数表示为数在线的一个点。在定义的帮助下,再对分数比较大小、理解等值分数、以及四五年级学习分数加减乘除四则运算,学生就能形成完整的逻辑系统。
伍教授这套书的定位是师资培训教材,其受众是中小学数学教师。他在《凤凰涅盘》(中译文见【22)中指出,
孩子的数学思维,技术的合理应用,师生互动,以及良好的教学实践等……对于教学是很重要的话题,但是它们还不足以将旧式数学体系改变成核心标准的体系课程。当务之急是,如何用师资培训来帮助教师们,把旧式数学转变成正确的、连贯的、精确的、合理的中小学数学。
也就是说,他认为数学的正确性是讲授数学的首要前提,而在符合学生认知水平的特点的基础上选择适合的方法和途径则可以作为辅助手段,使得同时满足所讲授的数学既是正确的,也是有趣的。
结语
总之,我们希望,所有的中小学数学教师能抽空读一读伍教授的这本书。这是一位数学家在对高等数学做过多年的深入研究以后再重新审视中小学数学的结晶。对于中小学生在学习数学中已经遇到的或将来可能遇到的种种问题,伍教授都做了深入的思考,并对这些问题给出了出色的回答。当然,“授人以鱼,不如授人以渔”,我们更需要学习的是这种方法与精神,即要去钻研学生可能遇到的困难,并努力直面问题给出解决方案,而不是回避和敷衍。这样的努力是值得的,正如著名英国数学家阿蒂亚(Atiyah)所说的(见【4】):
我们必须牢牢记住,数学是人类的一项活动。求解问题或做数学的目的大概是为了把我们获得的信息传递给后代。我们必须记住,人的智力是有限的,肯定不能连续不断地去领会和消化无穷多的问题并把它们全部记住。在很大程度上,理论的真正目的,着眼于把过去的经验加以系统地组织,使得下一代人——我们的学生以及学生的学生,能够尽可能顺利地汲取事物的本质内容。唯有如此,你才能不断地进行各种科学活动而不至于走进死胡同,我们必须设法把我们的经验浓缩成便于理解的形式,这就是理论之基本所为。也许我可以引用庞加莱在谈论这个话题时的所说的话:科学由事实建造,正如房屋由石头建造一样;但是事实的收集并非科学,正如石块的堆积并非屋宇。
古人云:博学之,审问之,慎思之,明辨之,笃行之。这就是伍鸿熙教授的真实写照。他不辞劳苦、兢兢业业、十年如一日地默默耕耘,就是为了让老师们明白数学原来是可以教的,最终让学生明白数学原来是可以学的,这也是我们所有数学教育工作者的共同目标。笔者深信,伍教授的著作一定会给我们提供许多借鉴和指导。为此,笔者郑重地向读者特别是中小学数学教师推荐伍教授的这套师资培训教材。
致谢
感谢对我们的写作给出极大帮助的各位老师和同学:首都师范大学外语系的张淑娥老师,数学科学学院的丁洁、雷艳萍、邵红亮、王丽芳、王盼盼、赵媛肖同学,北京市丰台一中的田双老师。
感谢伍鸿熙教授对笔者一如既往的热情帮助和支持。
感谢审稿人对初稿提出许多有价值的建议。
参考文献
C. L. Alexandersen,Morris Klein 访问记,刘钝译,《数学译林》,第 8 卷(1989 年)第 4 期,pp332–341.
V. I. Arnold,新蒙昧主义与俄罗斯教育,袁钧译,《数学译林》,第 25 卷(2006 年)第 1 期, pp13–25;第 2 期,pp108–121.
V. I. Arnold,中学需要数学吗?赵琳译,《数学译林》,第 25 卷(2006 年)第 3 期,pp250–258.
M. F. Atiyah,如何进行研究,收入《数学的统一性》,袁向东主编,江苏教育出版社,1995 年。
H. Bass,数学家应是教育家,蔡克聚译,《数学译林》,第 17 卷(1998 年)第 4 期,pp344–348。
H. Bass,数学,数学家和数学教育,林长好译,《数学译林》,第 25 卷(2006 年)第 4 期, pp367–377。
C. T. Chong and Y. K. Leong,Jean-Pierre Serre 访问记,张伟平、陈军译,《数学译林》,第 6 卷(1987 年)第 3 期,pp254–259.
M. Cook,Mathematicians, An outer view of the inner world, Princeton University Press, 2009. 有中译本《当代大数学家画传》,林开亮等译。
丁洁、赵洁,根深叶茂,源远流长——记伍教授北京数学教育之行,《数学通报》,2011 年第 11 期。
R. P. Feynman, New Textbooks for the ”New” Mathematics,中译文收入《费曼手札:不休止的鼓声》pp513–520,叶伟文译,湖南科学技术出版社,2008 年。
H. Freudenthal,《作为教育任务的数学》,陈昌平、唐瑞芬等编译,上海教育出版社,1995 年。
P. A. Griffith,数学:从伙计到伙伴,黄乐华译,《数学译林》,第 13 卷(1994 年)第 3 期, pp246–255。
胡作玄、石赫,《吴文俊之路》,上海科学技术出版社,2002 年。
姜伯驹,关于初中数学课程标准的“基本理念”,《数学通报》,第 44 卷(2005 年)第 8 期, pp1–4。
F. Klein,《高观点下的初等数学》,共三卷:第一卷《算术、代数、分析》与第二卷《几何》,舒湘芹,陈义章、杨钦梁译;第三卷《精确数学与近似数学》,吴大任、陈 [受鸟] 译,台北,九章出版社,1996 年。
L. Lov´asz,数学的趋势:它们会怎样改变教育?,李乔译,《数学译林》,第 29 卷(2010 年)第 2 期,pp178–184。
苏步青,大学要关心中小学教育,收入《苏步青文选》,pp139–141,浙江科学技术出版社,1991 年。
伍鸿熙,一个数学家在数学教育界的经验,《数学通报》,第 47 卷(2008 年)第 1 期,p6。
H. Wu, Understanding Numbers in Elementary School Mathematics,American Mathematical Society,2010。中译本《数学家讲解小学数学》,赵洁、林开亮等译。
H. Wu,Teaching School Mathematics: Pre- Algebra, Teaching School Mathematics: Alge- bra,American Mathematical Society,2016。
H. Wu, Mathematics of the Secondary School Curriculum I, II, III,(2018 年将出版)。
H. Wu,Phoenix Rising-Bring the Common Core State Mathematics Standard to Life, American Educator,Fall 2011,pp. 3–13. 中译文《凤凰涅盘——让核心数学标准焕发生机》,赵洁译,《数学通报》,2012 年第 4 期,p1。
H.Wu,Mis-education of Methematics Teacher,Notices of AMS,58(2011), No.3, pp372-384. 中译文《数学教师的错误教育》,李晓莉译,《数学译林》,2012 年第 2 期,p143–155。
吴大任,博洽内容、独特风格——介绍克莱因《高观点下的初等数学》,《数学通报》,1989 年第 6 期,收入《吴大任教育与科学文集》,崔国良主编,南开大学出版社,2004 年。
吴文俊,中国古代数学对世界文化的伟大贡献,收入《吴文俊文集》,山东教育出版社,1986 年。
吴文俊,大国对数学教育应有的态度,《上海教育》,2011 年 17 期。
袁隆平、辛业芸,《袁隆平口述自传》,湖南教育出版社,2010 年。
张奠宙,陈省身谈中国数学教育,《高等数学研究》,2005 年第 02 期。
张英伯,与伍鸿熙教授座谈摘要,《数学通报》,2006 年第 45 卷第 7 期,p1。
相关链接
| 作者简介: | 林开亮,西北农林科技大学理学院 |
| 赵洁,北京景山学校朝阳学校 |





