雪花里的数学

善科文库团队 2019-02-24 14752

蒋迅

每当看到漫天飞舞的雪花时，都会惊异于大自然的奇妙力量。这时映入许多人脑海中的第一个问题往往是──每一片雪花都是不同的吗？美国《国家地理》与《生命科学》给出了大相径庭的答案，有人甚至宣布发现了两个完全一样的雪花。其实这并不难理解。专家们估计，每年有 10 的 24 次方个雪片飘落下来，从统计学的角度说，当然很可能有相同的雪花。但这种“数学”问题并不是我们要讨论的。如果试图穷举雪花图形的话，我们就走进了一个死胡同，因为我们更感兴趣的是，人们能否用数学作为工具彻底解决雪花形成的奥秘：它们有多少种？它们是在什么条件下形成的？它们能否在计算机上模拟？

一，雪花研究史

漂亮的雪花Source:SnowCrystals.com

当我们看到这些漂亮的雪花时，我们一定对大自然的奇妙力量而感到神奇。有人说，每一片雪花 (snowflake) 都是不同的。真是这样吗？美国《国家地理》有一篇文章说这很可能是真的。《生命科学》(LiveSciecne) 上刊登了一篇文章指出雪花是可能重复的。有人甚至宣布发现了两个完全一样的雪花。其实这并不难理解。专家们估计，每年有 1024 个雪片飘落下来，从统计学的角度说，当然很可能有相同的雪了。不过笔者对这样的“数学”问题并不感兴趣。我们更感兴趣的是，人们能否用数学作为工具彻底解决雪花形成的奥秘：它们有多少种？它们是在什么条件下形成的？它们能否在计算机上模拟？

让我们再多看一些雪花吧。下面是美国国家地理杂志提供的一些照片。

Source:National Geographic Photography

如果我们试图穷举雪花的图形的话，我们就走进了一个死胡同，因为我们是不可能收集所有的雪花图形的，这样做只能让我们更加迷茫。为了从数学上研究雪花，让我们首先来了解一下人类对雪花认知的历史。

让我们首先来了解一下人类对雪花认知的历史。人类对雪花的研究已经有上千年了。松鼠会有一篇桔子作为新年礼物奉献给读者的走笔优美的“雪花史”。维基百科也有一篇“雪花研究史”，记录追述到西汉经学家韩婴。

雪花也是数学家感兴趣的课题。1611 年，天文学家和数学家开普勒就预言，六角结构反映出位于其下的结晶结构。二十六年后 (1637 年)，数学家和哲学家笛卡尔第一次详述了雪花的外形。几乎是同时，英国博物学家、发明家罗伯特·胡克(Robert Hooke) 在他 1665 年出版的《显微图谱》（Micrographia) 中描述了雪花的结晶。此后对雪花的研究就在很长一段时间内处于停滞的状态。

班特雷雪花Source:wikipedia.org

在研究雪花的历史里，有一位不能不提的是美国农民维尔森·班特雷 (Wilson Bentley)。他在少年时代就开始对雪花感兴趣。他的母亲送给他一个显微镜，他就在显微镜下观察雪花并随手画下来。但是雪花融化得太快了。正好市场上有了大画幅相机，班特雷倾其所有买下了昂贵的相机。在经过了一番挫折后，他终于在 1885 年 1 月 15 日拍下了第一张雪花照片。值得一提的是，他拍摄雪花的技术事实上一直延续至今。他一生一共拍摄了五千多张雪花照片，这些照片对于科学家和数学家影响巨大。通过自己的亲身观察他得出结论：没有两个雪花是相同的(不知道这是不是第一次书面的记录)。2010 年，他拍下的最早的雪花照片在纽约拍卖，每张 4800 美元。不过他在世时却少有人问津。尽管有一些机构购买了他的作品 (比如美国《国家地理》，请读另一篇)，但远远不够他在拍摄雪花中的投入。所以他一直过着贫困的日子。1931 年 12 月 23 日是一个暴风雪的日子，身患肺炎的他却坚持步行出去拍摄雪花，不幸的是他体力不支终于倒在了荒野中。班特雷远非一位数学家，但他是一位在雪花史中不能不特写的人物。

对雪花的研究迈出一大步的是日本物理学家中谷宇吉郎 (Ukichiro Nakaya)，他在 1930 年代第一次把雪花分了类，并首次在实验室实现了人工结晶。在此基础上，他制作了一个雪花形态图表。用他的这个图表可以预测在任何给定温度和饱和水平条件下的雪花的主要类型。通过班特雷、中谷宇吉郎等人的努力，人们把雪花大体分为 80 种类型，其中一种叫作“其它”，意味着这项工作还应继续下去。这个分类被称为“Magono-Lee 类”。

关于班特雷和中谷宇吉郎，还是去读桔子的精彩“雪花史”吧，现在让我们继续讨论雪花里的数学。

二，计算机的辅助

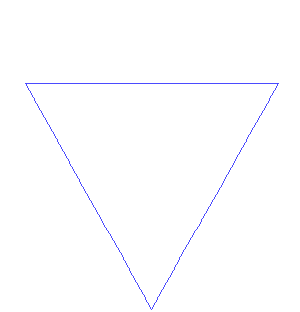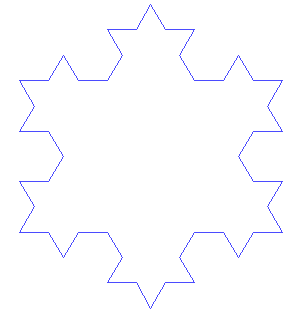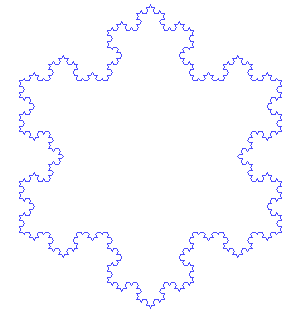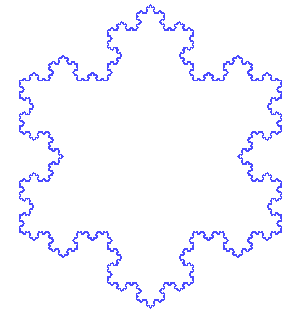科赫雪花Source:wikipedia.org

在二十世纪开始时，对雪花的研究向几何方法上发展。1904 年，海里格·冯·科赫(Helge von Koch) 发表了一篇论文“关于一个可由基本几何方法构造出的无切线的连续曲线”，描述了科赫曲线的构造方法。这是最早被描述出来的分形曲线之一，这就是著名的科赫雪花(Koch snowflake)。这个例子在“雪花中的数学”一文中提到过。虽然“科赫雪花”不是真正意义上的雪花模型，但是科赫的方法─在多面体上无限地改进─与班特雷使用的图解方法异曲同工。目前，人们所知道的是，雪花的基本构造是基于天然冰之分子的六边形。但人们对水汽到底是如何如此自我精心设计成美丽的雪花仍然知之甚少。

1986 年，美国混沌理论方面的物理学家诺曼·帕克 (Norman Packard) 提出了一个极其简单的格状自动机模型 (Lattice models for solidification and aggregation)。帕克是对结晶过程提出他的模型的，当然对雪花也适用。格状自动机也叫细胞自动机，最早是由冯·诺依曼在 1950 年代为模拟生物细胞的自我复制而提出的。而帕克则是注意到了结晶的自我复制机制。这一步为人们在计算机实现数字雪花打开了大门。


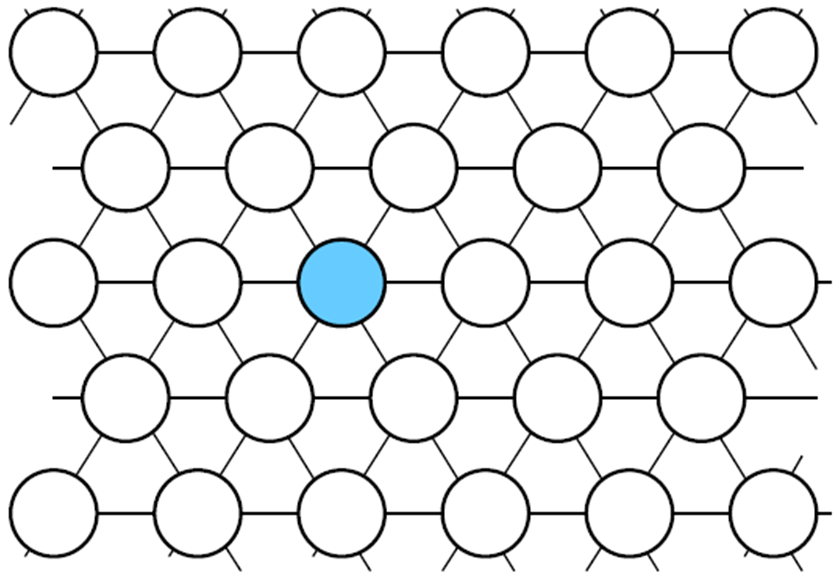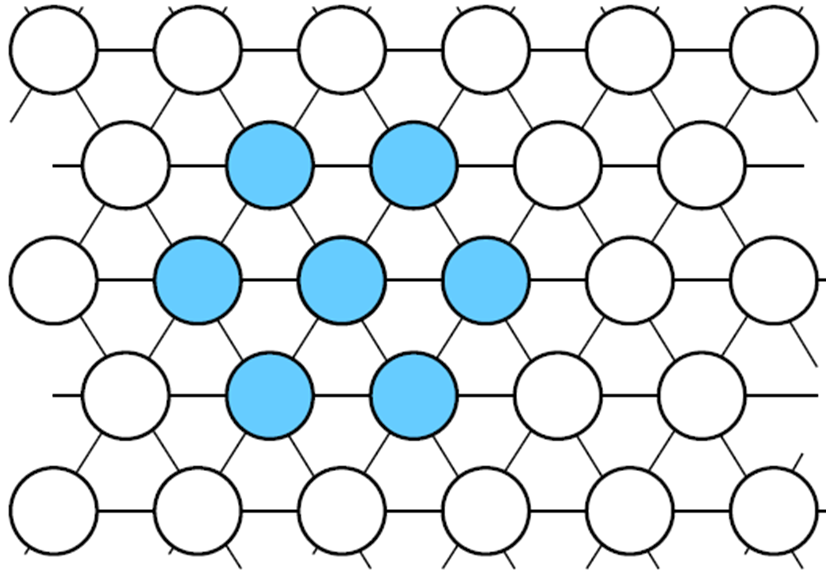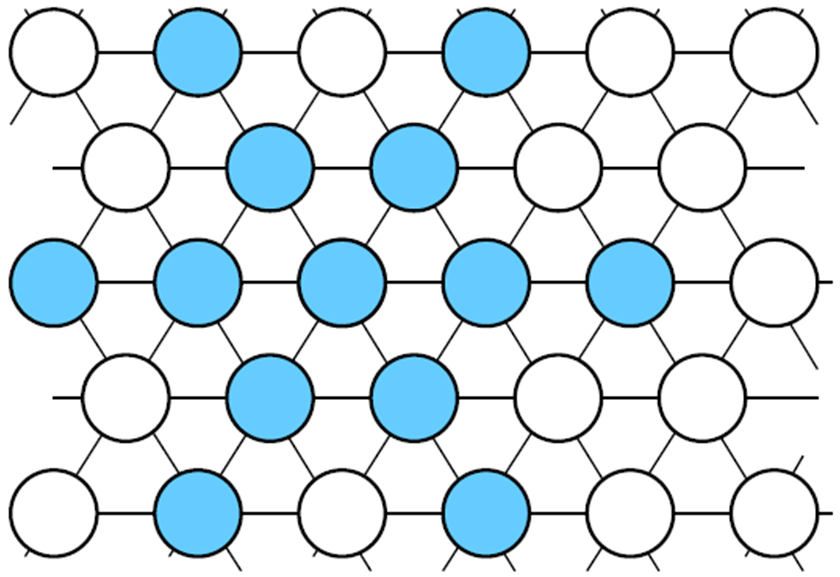第一步	第二步	第三步

帕克雪花 Hex 1

帕克还注意到雪花的自我复制是在尖头上，所以他做了一条假设：如果一个节点只有一个邻居是结晶的，那么这个节点就结晶，如果有两个是结晶了的，那么这个节点就不结晶；当然已经结晶了的节点保持结晶。这个过程无限重复。上图显示了在重复两次之后的效果。这只是其中一种假设。还有其它的假设，就导致不同形状的雪花图形。比如，可以假定当有 1 个、3 个或 5 个邻居是结晶时，这个节点就被结晶。为后面叙述方便，我们把第一种结晶法则称为“Hex 1”，把第二个称为“Hex 135”。这样的选择法则在 {3, 4, 5, 6}这四个邻居数量上可以不同，一共有 16 种法则。上图是我们说的第一种选择法则 Hex 1 过程的第一、二、三步。史蒂芬·沃尔夫勒姆(Stephen Wolfram) 研究了这种选择法则，他在观察了 30 步之后，得出结论：

人们预计在一片特殊雪花生成的过程中会在树状和面状两种状况里交替，新的分支不断生成但又互相碰撞。如果我们观察真正的雪花，一切迹象表明，这正是所发生的事情。事实上，一般地说，上面的简单的格状自动机似乎显然成功地复制了雪花生成的所有明显的特徵。

上面的讨论中，我们默认了一个事实：在一个迭代过程中，雪花一直保持著同一个法则扩散。但显然在自然界中的雪花不一定是按照一个固定的法则扩散的。很有可能，第一步遵循“Hex 1”，第二步就变成了“Hex 135”，第三步又成了“Hex1345”。这样的格状自动机模型也有人考虑过。

从这个例子，我们看到了计算机模拟开始扮演重要的角色。帕克的这一步是成功的，因为帕克生成的雪花即使让一个小学生去看，他也会说出那是一个雪花 (Steven Levy语)。还有一点更重要，正如沃尔夫勒姆说的：通过计算机模拟可能是预测某些复杂系统如何发展的唯一途径。……生成“帕克雪花”模式的唯一可行的方法是由计算机模拟。

三，物理学的帮助

比较帕克雪花和真实雪花 (格拉夫纳提供)

但是帕克方法还是有局限性的，人们对雪花的物理属性的认识还必须深入。让我们再回到物理学家在这方面的努力来。有时候对自然界的认识就是这样通过数学家和物理学家的相互促进完成的。在加州理工学院有一位天体物理学教授肯尼思·利伯布莱切特 (也译为利波瑞特，Kenneth Libbrecht)。他 1984 年毕业于普林斯顿大学，获得博士学位，现任加州理工学院物理系主任。利伯布莱切特是学天文学的，但他近年来对雪花做了大量研究。这多么像 400 年前的开普勒啊。一开始利伯布莱切特完全是出于好奇，但很快他就把好奇与自己受到的数学、物理学方面的严格训练结合到一起，成为了一名研究雪花微观世界的自觉的科学家。

虽然雪花千变万化，但科学家感兴趣的是：用多少种雪花形成的不同过程。换句话说，有多少种不同类型的雪花。在这一点上利伯布莱切特和中谷宇吉郎不谋而合。利伯布莱切特把雪花的分类从中谷宇吉郎等人的 80 种简化到35 种。现在比较标准的平面结晶分类是 19 种─ 13 个Magono-Lee 类，6 个利伯布莱切特类，都是六边形的形状。对雪花分类的意义在于，虽然人们不可能用计算机复制所有的雪花，但是可以试图复制全部的雪花类形。

对雪花分类的意义还在于，人们可以针对雪花的每一类给出一个比较合理的物理解释。下面这些图片是利伯布莱切特利用特制的雪花显微照相机拍摄的，展示的是在安大略北部地区、阿拉斯加州、佛蒙特州、密歇根州上半岛以及加州内华达山脉地区飘落的雪花。下面是他对几种雪花给出的描述解释。


六棱柱状雪花：这是雪晶最为基本的形状。类似这样的雪晶个头通常很小，极少能够用肉眼进行观察。六棱柱状雪晶是绝大多数雪花开始时的样子，之后才是从 6 个角长出“枝杈”，形成更为精细的结构。	普通棱柱状雪花：这与上一种类型比较相似，所不同的是，它的表面装饰着各种各样的凹痕和褶皱。	星盘状雪花：这种薄薄的盘状雪晶拥有 6 个宽大的“枝干”，形成与星星类似的形状。它的表面经常装饰着极为精细的对称性花纹。盘状雪花在气温接近零下 2 摄氏度或者接近零下 15 摄氏度时形成，是一种比较常见的雪花类型。

扇盘状雪花：这也是一种星盘状雪晶，所不同的是，在邻近的棱柱表面之间长有与众不同的指向边角的脊。	树枝星状雪花：这种外形的雪晶个头很大，直径通常可达到 2 到 4 毫米，可以很容易用肉眼观察。	树枝星状雪花：这种树枝星状雪晶的枝干生有大量边枝，看起来很像蕨类植物。它们是所有雪晶中个头最大的，经常是带着直径达 5 毫米或者更大的身躯降落地面。尽管是个“大块头”，但它们只是单一的冰晶──水分子首尾相连而成。

空心柱状雪花：这是一个六角形柱体，两端拥有锥状中空结构。空心柱状雪晶个头很小，需要使用放大镜才能看到空心。	针状雪花：针状雪晶是一种身材“苗条”的柱体，在大约零下 5 摄氏度时形成。如果飘落在袖子上，你很有可能将它们误认为白头发。当温度发生变化时，雪晶形状便会从薄而扁平的盘状变成细长的针状，这也是它们最为奇妙的一个所在。至于为什么会上演这种变化，仍旧是科学界尚未揭开的一个谜团。	冠柱状雪花：这种雪晶首先长成队邙粗的柱状，而后被吹进云层的一个区域并在那里变成盘状。最后，两个薄薄的盘状晶体在一个冰柱的两端生长，形成图片所示的冠柱状。

罕见的 12 条枝杈雪花：这种雪花实际是由两片雪花组合而成的，其中一片相对另一片进行了 30 度旋转。类似这样的雪花非常罕见。	三角晶状雪花：在温度接近零下 2 摄氏度时，雪盘“生长”成被截去尖角的三角形，此时，图片中的雪晶就形成了。三角晶状雪晶同样非常罕见。	霜晶状雪花：云是由无数小水滴构成的，有时候，这些小水滴与雪晶发生碰撞并最终粘在一起。这种冻结的水滴被称之为霜。
Source:新浪科技

通常的雪花是正六边形的，但是我们发现也有其他形状。现在，通过在可控制的实验室条件下，人们可以培育雪花。科学家发现雪花形状在很大秤谌上取决于温度和饱和度。下面的图就是雪花在不同条件下形成的形状。

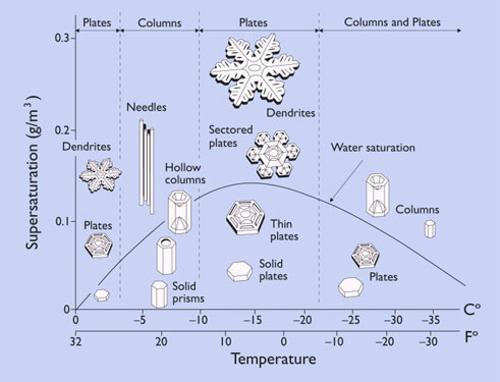雪花形状与温度、饱和度的关系 Source:SnowCrystals.com

这张图告诉我们，在通常条件下，雪花都是正六边形的。这一点在现在的科学理论框架下不难理解。松鼠会上的文章做了一个清晰的解释：雪花由水分子组成。“一粒沙子见世界”，小单元是六边形，当水分子以不同速度粘到这个单元的各个表面，最终形成的大雪花便也是六边形。后边，我们还将对这个图做一些讨论。

利伯布莱切特的研究得到了世人的注意。2004 年，利伯布莱切特获得了美国“国家户外图书奖” (National Outdoor Book Award)。2006 年，美国邮政局把利伯布莱切特的四个雪花图片印到了当年的圣诞邮票上。2010 年，瑞典把“伦纳德·尼尔森奖”(Lennart Nilsson Award) 授予他。他的工作把数学、物理和化学转化成了完美的图案，让人们从微观看到了千变万化的大自然是有其内在规律的。

从 1980 年代起，物理学家和数学家开始寻找和理的数学模型。他们的途径包括：表面张力模型、蒙特卡罗方法、偏微分方程、元胞自动机、混沌理论等。到 1990 年代，有人研究了描述类液层的连续状态模型的偏微分方程的边界值问题。所有这些努力为数学家建立合理的数学模型做好了准备。现在，数学家可以披挂上阵了。

四，元胞自动机模型

Source: Janko Gravner

在数学家中，首先应提到的是加州大学戴维斯分校的杨可·格拉夫纳教授 (Janko Gravner) 和威斯康星大学麦迪逊分校的大卫·格里夫耶斯教授 (David Griffeath) 的工作是最出色的。他们花费了四年的时间终于开发出了一种电脑模型，可以随意模拟出具有对称平衡之美的雪花的数学模型(Gravner-Griffeath Snowflakes，见视频)。格拉夫纳和格里夫耶斯的模型对雪花的生成提供了一个令人瞩目的数学基础。

Source:Gravner-Griffeath

格拉夫纳他们从 2005 年起开始研究雪花模型，2006 年开始建立 3D 模型并在 2007 年基本完成了建模。他们的工作首先从二维开始。他们对于帕克雪花进行了深入研究，得到了一些不可思议的结果。比如，他们从数学上严格地证明了帕克雪花的“密度”都是严格小于 1；他们还证明了一个有悖直觉的结论：Hex 14 的密度大于 Hex 134。

前面说过，帕克雪花一直保持着同一个法则扩散，但在自然界中的雪花不一定是按照一个相同的法则扩散的。虽然有人考虑过这样的格状自动机模型，但从数学上研究其可行性还是未知的。

Source: Janko Gravner

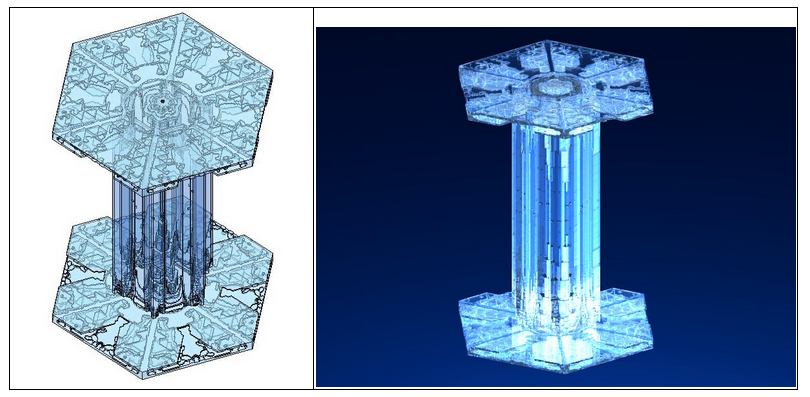
在此基础上，他们又向前迈了一步，而这一步是突破的一步，是使人类对雪花的认识又更上一层楼的一步。他们把雪花结晶的动力学归入粒子系统的流体动力学 (hydrodynamics of particle systems)，以雪花的物理原理为基础，并力图在介观体系(Mesoscopic) 的层次上抓住雪花形成过程中的物理、化学特徵，运用非线性动力系统中三维耦合映像格子 (coupled lattice map) 模型和布朗运动理论中的粒子内部扩散限制聚集(internaldiffusion-limited aggregation) 模型，深刻描述了雪花的结构形态。在研究中大量运用了随机过程、统计物理和偏微分方程理论的新成果，并把它们交会到一起。另外，他们建立的模型也从二维推广到了三维。图 9 显示的就是其中之一：左边是用 Matlab 生成的图像，右边是在左图基础上用光线跟踪软件 POV-Ray 加工后的效果。我们不可能把他们的结果全部介绍出来，仅仅用下面一组方程式来让大家看一看其复杂度。

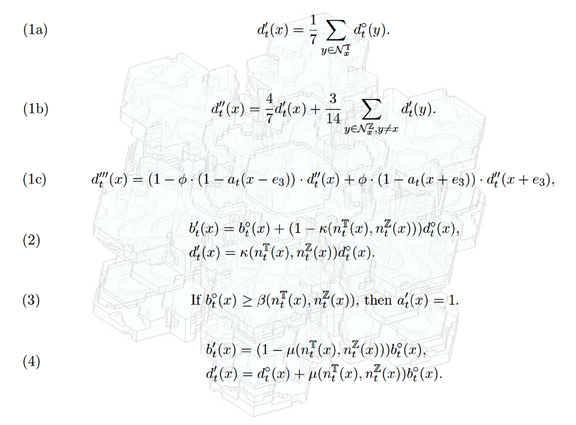Source:http://demianrepucci.com

细心的读者可能发现前面的雪花中有一个是三角形(还有十二边形的)。人们几百年前就注意到了这种形状，但一直无法解释。尽管三角形雪花很少，他们在实验室里看到的三角形雪花比统计模型显示的要多。这说明，在自然界里的三角形雪花也应该更多，更经常。他们还注意到，有些雪花虽然是六边形的，但仔细看的话，你会发现，它们有三条边长一些，而另三条边短一些，所以从总的形状上看，它们其实是三角形的。三角形雪花与温度、湿度似乎没有紧密的关系。利伯布莱切特提出一种假设：在雪花飘落的过程中，有时一条边会沾上一点点尘埃。这造成了雪花飘落时向上倾斜，而在下面的一条边会在风的作用下更快地成长，使得雪花变成了稳定的三角形。当雪花成了三角形形状之后，它就一直保持着这种形状。

格拉夫纳他们也研究了三角形和十二角形雪花。不过，他们不是按利伯布莱切特的解释做的模拟。他们是从一开始就假定雪花的生成元是三角形的，因此最后生成的雪花也是三角形的。这似乎与利伯布莱切特的猜测不同。其实关键是利伯布莱切特所说的尘埃的影响是在什么时候发生的。如果是在雪花核一开始就已经发生了的话，那么利伯布莱切特的说法就和格拉夫纳的假定相吻合了。当然这个解释还不具有太大的说服力。仔细观察的话可以注意到，自然界的雪花很多都是不对称的。有理由猜测这样的雪花从一开始就是不对称的。三角形雪花只是一个特例。也许，最终的答案还要数学家们去解决呢。

2008 年 1 月，加州大学戴维斯分校宣布了格拉夫纳他们的工作。随后，包括路透社、发现频道、芝加哥论坛、洛杉矶时报、科学日报等媒体对他们的工作加以报导。可以说，他们的工作在数学领域上开创了一个新的领域。

Source:NASA

NASA 科学家汤姆·克鲁恩（Tom Clune）和郭国森在他们的基础上研究了雪花形成的数学模型。他们在计算机模拟过程中间有意改变代表物理量的参数值，得到了一些有趣的结果。上面的图片就是先选取适合纵向增长然后在中途变成适合横向增长的参数所得到的雪花图片。图 11 与格拉夫纳和格里夫耶斯的图 8 非常相像，因为他们借鉴了格拉夫纳和格里夫耶斯的模型，也使用了软件光线跟踪软件 POV-Ray。重要的是，他们把格拉夫纳和格里夫耶斯的算法在集群计算环境里利用“讯息传递介面”（MPI）和“区域分解方法”来实现并行计算。特别地，他们没有局限于原来的对称性限制。因此更容易实现在现实中常见的非对称雪花结晶。NASA 还建立了一个雪花数据库。NASA 更感兴趣的是更感兴趣的是宇宙冰。

现在，在计算机上实现一片雪花已经不是一个太难的事情了。如果读者有兴趣的话，也可以自己在计算机上“制造”出雪花来。格拉夫纳和格里夫耶斯提供了他们的MATLAB 程序。不过，因为 MATLAB 是 Scripting 语言，所以运行起来可能会比较慢。还有一个办法就是笔者前面提到过的分形，最早、最著名的科赫雪花(Koch snowflake) 就是其中之一。

五，相变的有限元解

Source:Scientific American

还有一个研究以相变(phase transition)为出发点。相变是指物质在外部参数（如：温度、压力、磁场等等）连续变化之下，从一种相（态）忽然变成另一种相，最常见的是在一定的条件下，冰变成水和水变成蒸气等，也有可能是相反的过程。我们把这样的过程称为相变。因为水和冰之间的边界不是褂讪的，所以它形成的热传导方程是一个自由边界问题。对这个自由边界的最简单描述 (或者说，最简单模型)就是在这个界面上，温度为零摄氏度。让我们考虑一个最简单的一维情况。这个情况和本文讨论的雪花问题不完全一样，但是也许可以帮助读者加深理解。假设在[0，+∞] 区域上的冰和水。假定在开始时整个区域都是冰。我们从左边提供一个热源，于是冰开始熔化，在 $t$ 时刻，区域 $[0，s(t)]$ 变成了水。忽略边界条件和初始条件，我们得到在 $[0，s(t)]$ 上的热传导方程：

$$\partial u / \partial t = \partial ^ { 2 } u / \partial x ^ { 2 } \quad ( x , t ) : 0 < x < s ( t ) , t > 0$$

这里，$u = u(x, t)$ 是温度，$s(t)$ 是自由边界。在自由边界上温度是零，所以 $u(s(t)，t) = 0$。注意自由边界 $s$ 是随时间而变的曲线 (或曲面)，我们还应该有一个在 $s$ 上的条件。最常见的就是著名的“史蒂芬条件”(Stefan Condition)：

$$\frac{\mathrm{d}s}{\mathrm{d}t}=-\frac{\partial u}{\partial x(s(t),t)},\quad t>0$$

也就是说，自由边界随时间的变化率和温度在自由边界上位移的变化率成正比，方向相反。相应的偏微分方程就是“史蒂芬问题”(Stefan Problem)。为了说明相变的性质，我们再稍微深入一步。物理实验表明，在自由边界上，温度达到零度，但不会立即继续升温。这里有一个积蓄能量的过程，直到增加了 L 单位的能量 (潜热) 后温度才会继续增长。让我们引入一个新的变量 y 来表示水的浓度，并假定 $L = 1$。我们定义 $v = u + Ly = u + y$。这里，$y$ 是阶梯函数：$y = 1$，如果 $0 < x < s ; \quad y = 0$，如果 $x > s ; \quad 0 < y < 1$，如果 $x = s$。

v 决定了相变的热动力。引入函数 $h ( z ) = \min ( z , 0 ) + \max ( z-1,0 )$。则上面的热传导方程可以写成：

$$\frac{\partial v}{\partial t} = \frac{\partial ^ { 2 } v}{\partial x ^ { 2 }}$$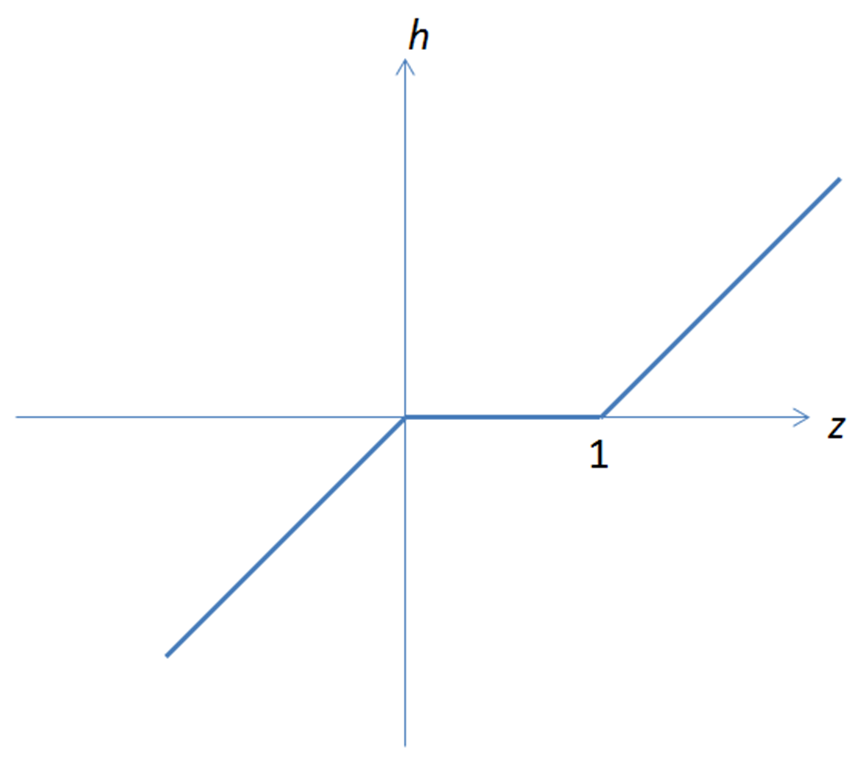

经过这个变换，上述方程在整个半实数轴 $(0，+∞]$ 上成立，温度 $u = h(v)$。方程本身成为退化的抛物形偏微分方程。这样做的好处在于，人们可以运用变分和有限元的方法在一个褂讪的区域里得到方程的数值解。

上面的讨论不是一个严格的讨论，只是希望帮助读者理解下面要介绍的相变的有限元解法的思想。从这样的描述看，雪花的形成问题应该是与相变问题紧密相关的，因为在第三节里我们已经看到，雪花是由水珠在一定的温度和饱和度条件下形成的，从这个意义来说，就是一个结晶的过程。从数学上说，人们需要做的就是研究自由边界表面随时间的变化。一片雪花的形成过程是否也能用相变的数学模型来描述呢？

2012 年初，英国伦敦帝国学院的约汉·巴瑞特 (John Barrett) 教授和罗伯特·纽伦伯格 (Robert Nurnberg) 教授与德国雷根斯堡大学的哈罗德·加克 (Harald Garcke) 教授就按照这个思路做出了一些新的工作：“雪晶体生长中分面格式形成的数值计算”(Numerical computations of facetted pattern formation in snow crystal growth)。这是他们在自由边界问题的有限元分析的成果之上对雪花研究方面的一个有意义的新尝试。

让我们先回到在第三节中的“雪花形状与温度、饱和度的关系”那张图。很明显，雪花的形状与温度和饱和度有关。当温度刚刚在冰点之下的时候，如果饱和度比较低的话，出现柱状雪花；如果饱和度比较高的话，就出现树突状雪花。当温度在 -5℃ 附近时，如果饱和度比较低的话，出现实心柱状雪花；如果饱和度比较高的话，就出现空心柱状雪花和针状雪花。当温度低到 -10℃ 以下时，如果饱和度比较低的话，出现实心盘状雪片；如果饱和度比较高的话，就出现树突状雪花。当温度到 -25℃以下时，如果饱和度比较低的话，出现实心盘状雪片；如果饱和度比较高的话，就又出现柱状雪花。从物理意义上说，雪花的形成过程是固体和气体的边界（即自由边界）变化的过程。而这个自由边界的变化是由于水分子的扩散和附着等过程。在这个过程中满足物质守恒定律，同时表面能量达到极小。另外我们知道，冰是一种六方晶系的晶体, 基本形态是六角形的片状和柱状。冰晶体的各向异性导致其物理性能（如导热性）随着方向的不同而有所差异。这种六边形的各向异性（hexagonal anisotropy）也必须考虑进去。巴瑞特、纽伦伯格和加克根据上述条件引入了一个与雪花相关的结晶(Crystallization) 的数学模型─准静态的扩散问题 (quasi-static diffusion problem)。

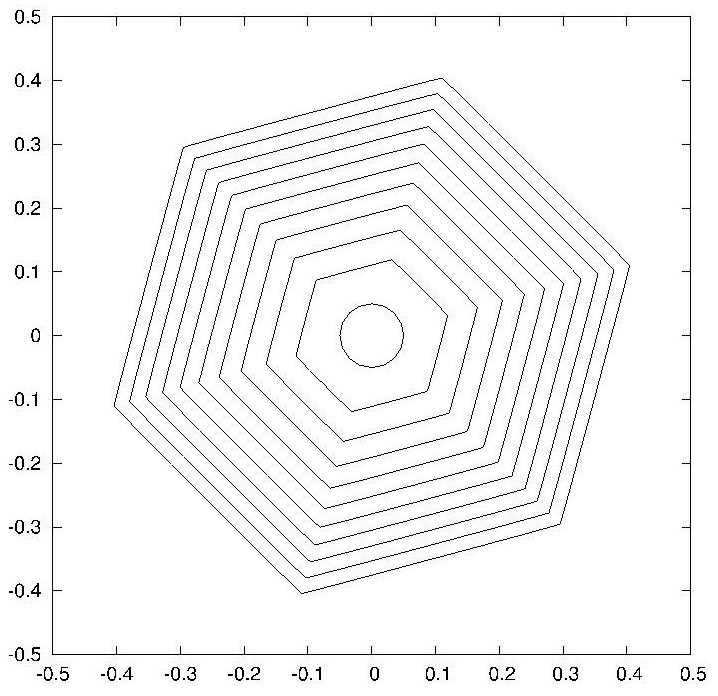
他们的巧妙之处在于把雪花的轮廓看成是一个自由边界，然后在自由边界上施加具有物理意义的复杂条件。对相应的偏微分方程建立其变分形式，以便运用有限元方法找到数值解。为了实现不同形状的雪花，在他们通过改变方程组里的饱和参数 $u_D=u_{∂Ω}$、凝结系数$β$和表面能量六边形的各向异性参数$γ$来实现。我们同样不准备对他们的方程组进行详细的讨论，而是转到数值计算上来。


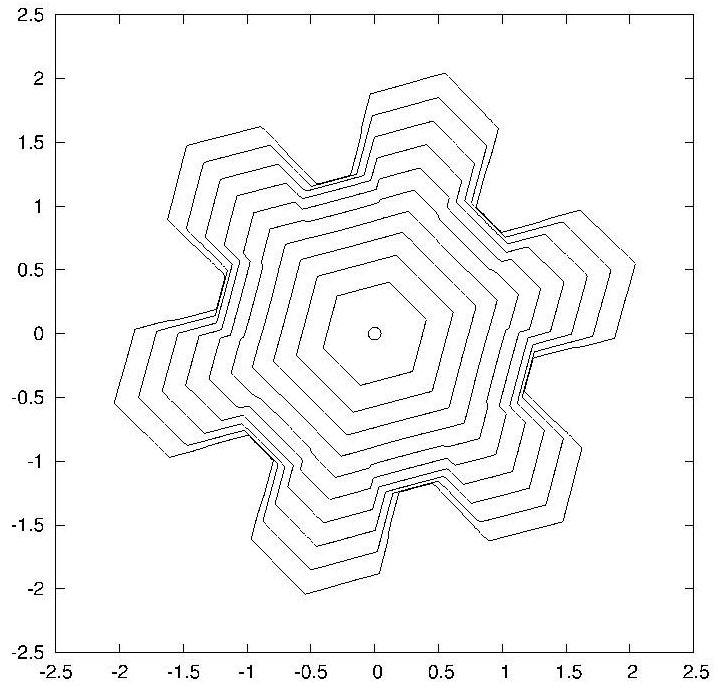$u_D = 0.004, γ = β = γ_{hex}.$
$t = 0; 5; ...; 50$	$t = 0; 50; ...; 500$

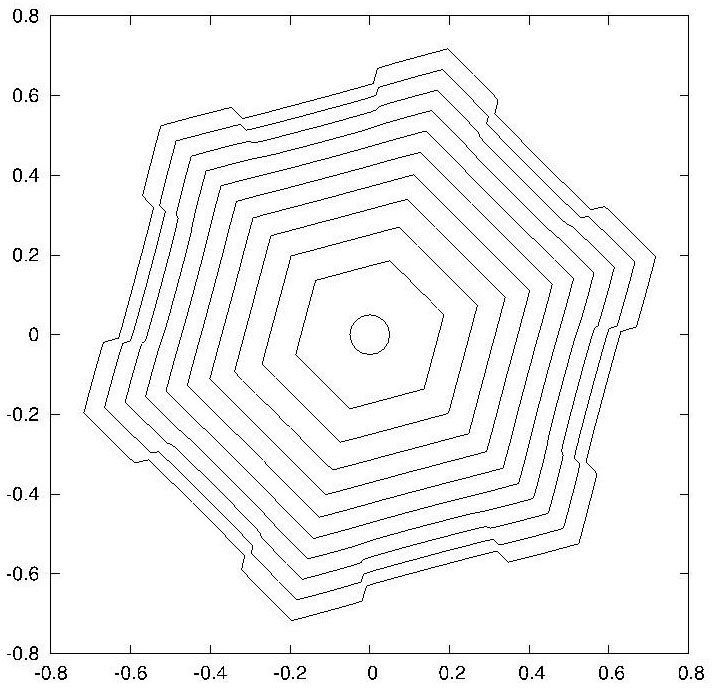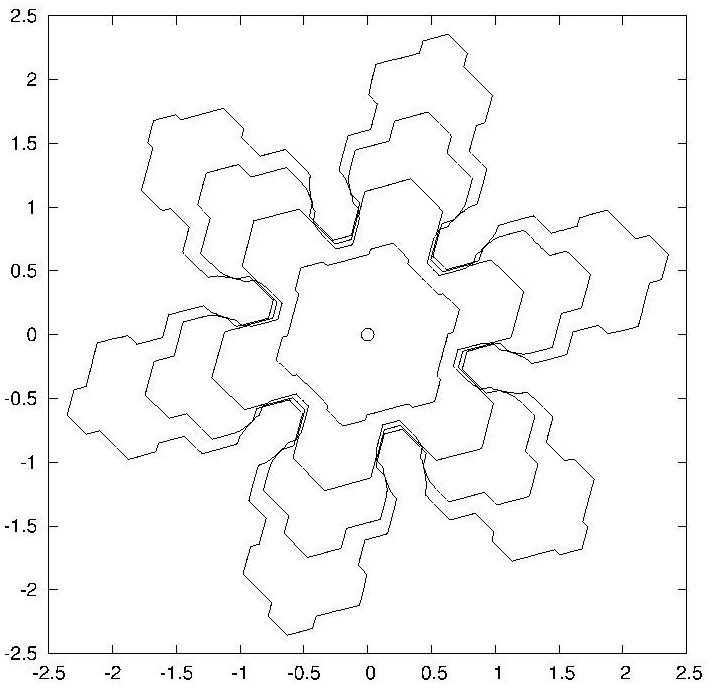$u_D = 0.01, γ = β = γ_{hex}.$
$t = 0; 5; ...; 50$	$t = 0; 50; ...; 200$

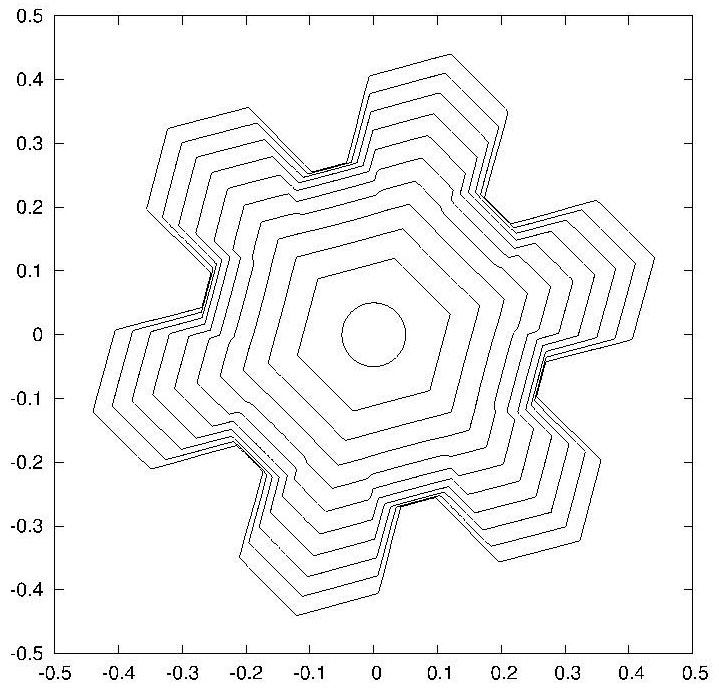$u_D = 0.04, γ = β = γ_{hex}.$
$t = 0; 0.5; ...; 5$	$t = 0; 5; ...; 40$

Source: Harald Garcke

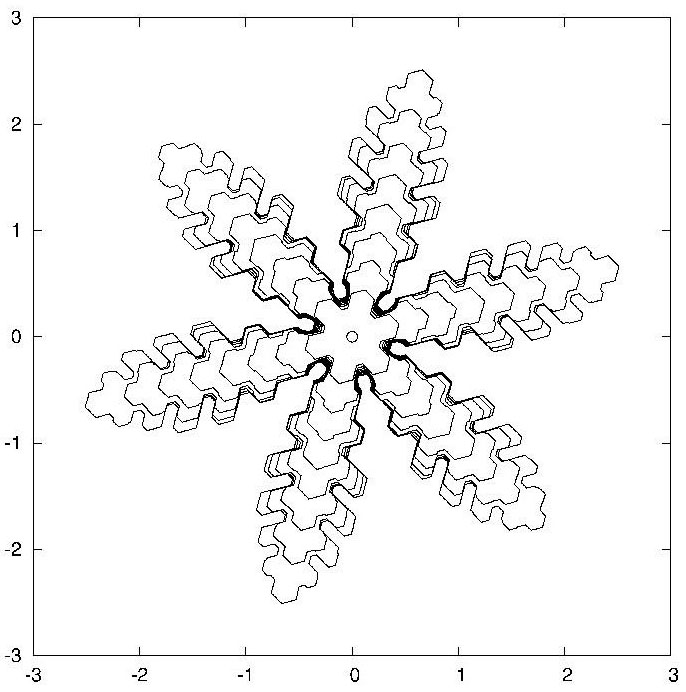
在建立了一组偏微分方程之后，他们进而用有限元方法进行了数值计算。上图就是他们数值计算的一些结果。为了方便观察雪花界面（即自由边界）随时间的变化，每一行中并列的的两个图分别记录了这个曲线在不同时间段的形状。注意这里的每张图都是多个界面的叠加图。我们看到，除了参数 $u_D$ 以外，其他参数都是相同的。这三个雪花分别由 $u_D = 0.004$，$0.01$ 和 $0.04$ 生成。从而从数学上解释了雪花形状和饱和度的关系。在他们的论文中有两类雪花：刻面 (facet) 和树突(dendrite)。这些图形都是在不同的参数选取下得到的。加克对科学美国人记者说，他们“是第一个用能量守恒和热力学理论同时实现这两种生长”的小组。

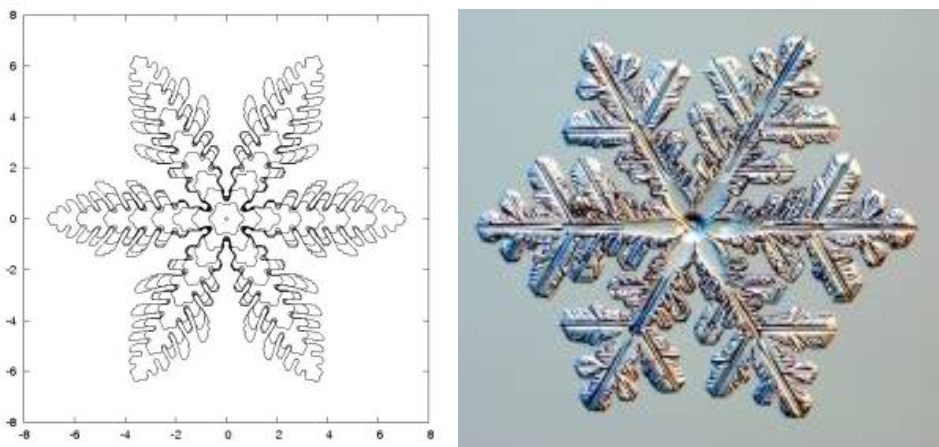Source: Harald Garcke

为了在计算机上模拟这组偏微分方程代表的雪花的生成，人们必须准确地描述结晶面 (即自由边界) 随时间的变化。人们通常是把这个曲面用不断加细的三角形来近似，这是有限元法所必须的。但这些三角形经常会退化从而导致模拟失败。他们的办法就是用现在比较时髦的平均曲率(Mean curvature) 来控制模拟以达到在计算机上实现的目的。他们表示，这个办法可以避免三角刨分蜕化的难点。笔者认为这是他们成果的一个亮点。

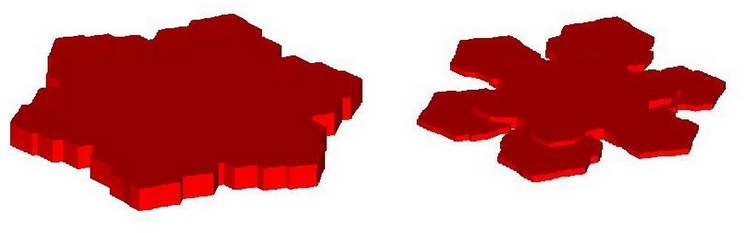Source: Harald Garcke

他们也对偏微分方程的数值解做了分析。他们发现，结晶体中表面分子的结合对结晶的生长有很强的影响。他们还发现，雪花尖端的生长速度与空气中的水蒸气的多少成正比。他们认为，雪花的结构源于扩散有限晶体生长在各向异性的表面能量和各向异性吸附动力。冰晶形态的稳定在很大秤谌上依赖于饱和、晶粒尺寸和温度。他们注意到了尖端速度和饱和度之间有线性关系。他们还得出结论，表面能量的影响尽管很小，却对雪花的形成有较大的影响。最后一点最为重要，它也许揭示了一个可能最后解决雪花形成问题的新的思路。

他们的模型─第一次用能量守恒和热力学理论建立的连续模型成功地研究了雪花的生成，这是此模型与格拉夫纳-格里夫耶斯模型的本质区别。由于这个原因，他们的途径自然地被物理学家所欣赏。重要的是，他们开辟了用偏微分方程和有限元方法研究雪花的新方向。麻省理工学院的“科技评论”(Technology Review)、英国的“邮件在线”(Mail Online) 以及“科学美国人”(Scientific American) 都报导了他们的成果。

在这里，笔者需要对“科学美国人”的报导做一点说明。“科学美国人”在文章中也提到了格拉夫纳和格里夫耶斯的工作，但把他们的工作误解成了在分子的层次上的格状自动机模型。其实，格拉夫纳和格里夫耶斯的工作是在介观体系的层次上，也就是说他们只是到了微米的范围。他们在论文标题上就写清楚了这一点。事实上，目前对雪花的形成人们还没有一个完美的解释。从物理上还无法在分子的层次上解释分子的附着和分离的机制。利伯布莱切特认为，可能有某个物理性质还没有被认识到，比如雪晶形状的不稳定性。在这样的情况下，在分子的层次上建立数学模型也就无从提起了。

有一个有意思的巧合是，德国雷根斯堡大学正是第一个研究雪花的天文学家和数学家开普勒逝世的地方。加克教授说，他们可以在办公室的窗前就见到真正的雪花。这是在加州洛杉矶的利伯布莱切特教授和在加州戴维斯的格拉夫纳教授不能享受的优越待遇。

六，雪花的快乐

一篇多少有些数学的短文到此应该收笔了。作为结尾，让我转引一下徐志摩的《雪花的快乐》。这首诗作于 1924 年 12 月 30 日，发表于 1925 年 1 月 17 日《现代评论》第一卷第 6 期：

假如我是一朵雪花，
翩翩的在半空里潇洒，
我一定认清我的方向──
飞扬，飞扬，飞扬，──
这地面上有我的方向。
不去那冷寞的幽谷，
不去那凄清的山麓，
也不上荒街去惆怅──
飞扬，飞扬，飞扬，──
你看，我有我的方向！
在半空里娟娟的飞舞，
认明了那清幽的住处，
等着她来花园里探望──
飞扬，飞扬，飞扬，──
啊，她身上有朱砂梅的清香！
那时我凭借我的身轻，
盈盈的，沾住了她的衣襟，
贴近她柔波似的心胸──
消溶，消溶，消溶──
溶入了她柔波似的心胸！

雪花飞来，一片两片三四片，飞入芦花总不见。微小轻盈的雪花能令诗人动心，让农民入迷。天文学家不放过它，数学家决心彻底解决它的奥秘。这就是雪花的威力。

致谢：笔者感谢格拉夫纳教授和加克教授提供多张图片！

后记：

“雪花里的数学”到此就发完了。我很感谢科学网上网友与我的互动，也感谢科学网编辑把本系列中的每一篇都放到了首页上，让更多的老师和同学们知道了雪花里的数学。我看到科学网上的很多网友写出的评论水平很高，有些评论颇具启发性。本系列分六次发表实因不得已。我尽量在每篇前后都加上了链接，以便读者对这个问题有全面的理解。我希望这个系列和网友们的评论能为对此研究感兴趣的数学物理工作者起到引导入门作用。如果能看到有谁独辟新路，更好地做出一个雪花的数学模型，那是我最高兴的事情了。
我在第 4 节里提到两位 NASA 科学家时说到：“重要的是，他们把格拉夫纳和格里夫耶斯的算法在集群计算环境里利用‘讯息传递介面’（MPI）和‘区域分解方法’来实现并行计算”。这句话是指相对于格拉夫纳和格里夫耶斯的计算有哪些不同之处，并不是说 NASA 的技术有多么重要，NASA 科学家也没有将他们的结果写成论文发表。科学网博主、中科院大气所一位硕士因为我这句话而表示对我本人和文中学者的轻视。对此，我只能表示遗憾。
有人说我的稿费一定很多。但《数学文化》杂志是不给稿费的。我在那里发文章是为了支持这个新的杂志，也希望有更多的读者喜欢并订阅这个杂志，使它能生存下去。写一篇这样的文章很花费时间，还没有报酬。我唯一的希望是，如果你不喜欢我的文章，不来读就好了。不必用语言来伤害我。科学网上有一些人喜欢用激烈的、文革大字报式的语言评论挖苦我们这些在这里写博客的人。我感觉，文革的土壤在知识分子中仍然存在，而且只要有适当的环境，文革还是有再次发生的危险。希望没有经历过文革的年轻人能读一读中国近代史，思考一下为什么有那么多的知识分子会去盲从，你自己在那样的环境下会不会干出极端的事情来？历史的悲剧不能重演。每个人都应该“从我做起”。顺便推荐林中祥老师的博文：“科学网中的‘不宜’”。

下面的参考文献是我挑选的。有兴趣做这项工作的老师同学们可以先从这些论文开始。

参考文献

"No Two Snowflakes the Same" Likely True, Research Reveals, National Geographic News, February 13, 2007.
Charles Q. Choi, "Scientist: Maybe Two Snowflakes are Alike", LiveSciecne, January 19, 2007.
Scientists discover snowflake identical to one which fell in 1963, NewsBiscuit, December 3, 2010.
雪花史，科学松鼠会，2008 年 12 月 25 日.
J. Kepler, "Strena Seu de Nive Sexangula," 1611. Translated as"TheSix-Cornered Snowflake," trans. Colin Hardie, Clarendon Press, Oxford,1966.
R. Descartes, "Les M' et' eores," 1637; ' ed. Adam et Tannery, Paris, Vrin, t. IV, 1965.
R. Hooke, "Micrographia," 1665; Dover, 2003.
U. Nakaya, "Snow Crystals: Natural and Artificial," Harvard University Press, 1954.
C. Magono and C. Lee, Meteorological classification of natural snow crystal , J. Fac. Sci.Hokkaido 2 (1966), 321-335.
H. von Koch, Sur une courbe continue sans tangente, obtenue par uneconstruction g' eom' etrique ' el' ementaire, Arkiv f 矣 r Mathematik,Astronomi och Fysik 1 (1904), 681-702.
N. H. Packard, Lattice models for solidification and aggregation,Institute for Advanced Study preprint, 1984. Reprinted in "Theory andApplication of Cellular Automata," S.Wolfram, editor, World Scientific,1986, pp. 305-310.
S. Wolfram, "A New Kind of Science," Wolfram Media, 2002.
S. Levy, "Artificial Life: The Quest for a New Creation," Pantheon Books, 1992.
K. Libbrecht, Morphogenesis on ice: The physics of snow crystals, Engineering and Science 1 (2001), 10-19.
K. Libbrecht, Explaining the formation of thin ice crystal plateswith structure-dependent attachment kinetics, Journal of Crystal Growth258 (2003), 168-175.
K. Libbrecht, The physics of snow crystals, Reports on Progress in Physics 65 (2005), 855-895.
K. Libbrecht, Observations of an Edge-enhancing Instability in Snow Crystal Growth near-15 C, arXiv:1111.2786 (2011).
K. Libbrecht, "Field Guide to Snowflakes," In preparation, 2006.
K. Libbrecht, P. Rasmussen, "The Snowflake: Winter' s Secret Beauty." Voyageur Press, 2003.
绝美雪花显微照片：形状各异结构精细，新浪科技，2008 年 12 月 11 日.
R. Fisch, J. Gravner, D. Griffeath, Metastability in theGreenberg-Hastings model. Ann. Appl. Prob. 3 (1993), 935-967. (SpecialInvited Paper.)
J. Gravner, D. Griffeath, Multitype threshold voter model andconvergence to Poisson─Voronoi tessellation. Ann. Appl. Prob. 7 (1997),615-647.
J. Gravner, D. Griffeath, Cellular automaton growth on Z2: theorems, examples and problems, Advances in Applied Mathematics 21 (1998),241-304.
J. Gravner, D. Hickerson, Asymptotic density of an automatic sequence is uniform, in preparation.
J. Gravner, D. Griffeath, Random growth models with polygonal shapes, Annals of Probability 34 (2006), 181-218.
J. Gravner, D. Griffeath, Modeling snow crystal growth I: Rigorousresults for Packard' s digital snowflakes, Experimental Mathematics 15(2006) 421-444.
J. Gravner, D. Griffeath, Modeling Snow Crystal Growth II: Amesoscopic lattice map with plausible dynamics. Physica D: NonlinearPhenomena 237 (2008), 385-404.
J. Gravner, D. Griffeath, Modeling snow crystal growth III: 3d snowfakes, in preparation.arXiv:0711.4020.
J. Gravner and D. Griffeath, Robust periodic solutions and evolution from seeds in one-dimensional edge cellular automata, in review.
J. W. Barrett, H. Garcke and R. Nurnberg, Numerical computations offacetted pattern formation in snow crystal growth, arXiv:1202.1272v1(2012).
J. W. Barrett, H. Garcke and R. Nurnberg, On stable parametricfinite element methods for the Stefan problem and the Mullins-Sekerkaproblem with applications to dendritic growth, J. Comput. Phys. 229(2010), 6270-6299
J. W. Barrett, H. Garcke and R. Nurnberg, Finite elementapproximation of one-sided Stefan problems with anisotropic,approximately crystalline, Gibbs--Thomson law, arXiv:1201.1802v1 (2012).
J. W. Barrett, H. Garcke and R. Nurnberg, On the parametric finiteelement approximation of Evolving hypersurfaces in R3, preprint.
H. Garcke, Kepler, Crystals and Computers-How mathematics andcomputer simulation help understanding of crystal growth, preprint.