陈省身:从三角形到流形
编者注:原文标题From Triangles to Manifolds,发表于The American Mathematical Monthly, Vol. 86, No. 5 (May, 1979), pp. 339-349。中译文发表于《自然杂志》第2卷,译者乃北大数学教授尤承业。
陈省身先生是国际知名的几何学家,在国际数学联盟设立有以他命名的Chern Medal, 以示对获奖人终身成就的表彰。陈省身先生一生致力于推动几何学与拓扑学的发展,不仅培养了丘成桐、格里菲斯、赛蒙斯等杰出学生,还积极促进着几何学与拓扑学的普及与教育。本文就是他一篇有名的通俗文章。他晚年定居南开,90岁高龄还为本科生讲授了微积分和微分几何,有兴趣的读者,可以参看这里的链接:
——林开亮
 几何大师陈省身
几何大师陈省身
一、几何
我知道大家想要我全面地谈谈几何。几何是什么,这许多世纪以来它的发展情况,它当前的动态和问题,如果可能,窥测一下将来。这里的第一个问题是不会有确切的回答的。几何这个词的含义,在不同的时期,不同的数学家有不同的看法。在欧几里得(Euclid)看来,几何由一组从公理引出的逻辑推论组成。随着几何范围的不断扩展,这样的说法显然是不够的。
1932年,大几何学家维布伦(O.Veblen)和怀特海德说(J.H.Whitehead)[1]:
“数学的一个分支之所以称为几何,是因为这个名称对于相当多的有威望的人,在感情和传统上看来是好的。”
这个看法,得到了法国大几何学家嘉当(E. Cartan)的热情赞同[2]。而分析学家, 美国大数学家伯克霍夫(G. Birkhoff)[3]则认为:
“令人担忧的是, 几何学可能最终只不过是分析学的一件华丽的直观外衣”。
最近,我的朋友韦伊(A. Weil)[4]说:
“从心理学角度来看,真实的几何直观也许是永远不可能弄明白的。在以前,它主要意味着三维空间中形象的了解力。而现在,高维空间已经把比较初等的问题基本上都排除了,形象的了解力至多只能是部分的或象征性的。某种程度的触觉的想象也似平牵涉进来了。”
现在,我们还是抛开这个有点玄乎的问题,来看一些具体问题为好。
二、三角形
三角形是最简单的几何图形之一,它有许多很好的性质。例如它有唯一的一个内切圆,并有唯一的一个外接圆。又例如九点圆定理,本世纪初几乎每个有一定水平的数学家都知道这个定理。三角形的最引人深思的性质与它的内角和有关。欧几里得说,三角形的内角和等于180度,或$\pi$弧度。这个性质是从一个深刻的公理——所谓的平行公理——推出的。想绕开这个公理的努力都以失败终告,但这种努力却导致了非欧几何的发现。在非欧几何中,三角形的内角和小于$\pi$弧度(双曲非欧几何)或大于$\pi$弧度(椭圆非欧几何)。双曲非欧几何是高斯(Gauss)、鲍耶(JanosBolyai)和罗巴契夫斯基(Lobachevsky)在19世纪发现的。这一发现是人类知识史上最光辉的篇章之一。
三角形的推广是 $n$ 角形,或叫 $n$ 边形。把 $n$ 角形割成 $n-2$ 个三角形,就可看出它的内角和等于 $(n-2)\pi$。这个结果用外角和来叙述更好:
任何n角形的外角和等于2$\pi$,三角形也不例外。
三、平面上的曲钱,旋转指数与正则同伦
应用微积分的工具,就可以讨论平面上的光滑曲线,也就是切线处处存在且连续变化的曲线。设 $C$ 是一条封闭的光滑定向曲线, $O$ 是一定点。 $C$ 上每一点对应着一条通过 $O$ 点的直线,它平行于 $C$ 在这点的切线。
如果这点按$C$的定向跑遍$C$一次,对应的直线总计旋转了$n$圈。我们称整数$n$为$C$的旋转指数。见图1。
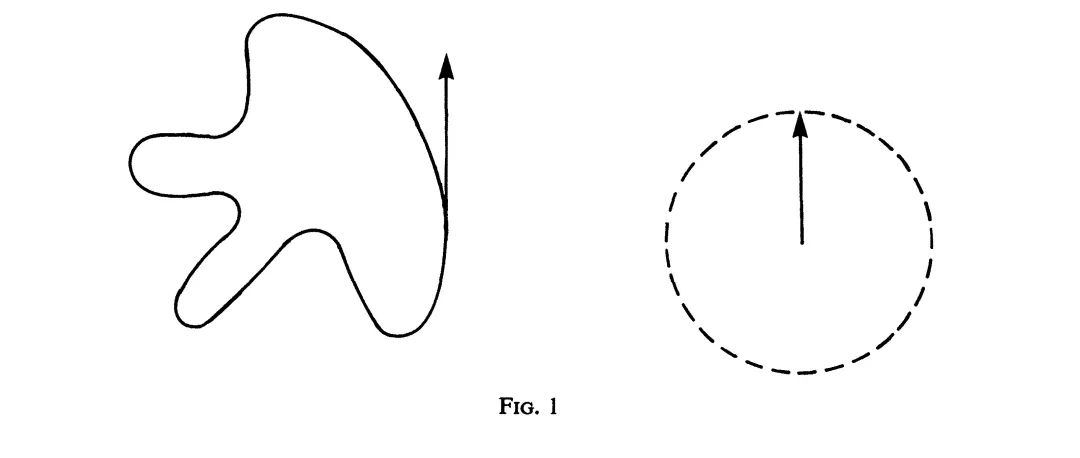
微分几何中的一个著名的定理说:
若 $C$ 是简单封闭曲线,也就是说 $C$ 自身无交叉点,则 $n=±1$ 。
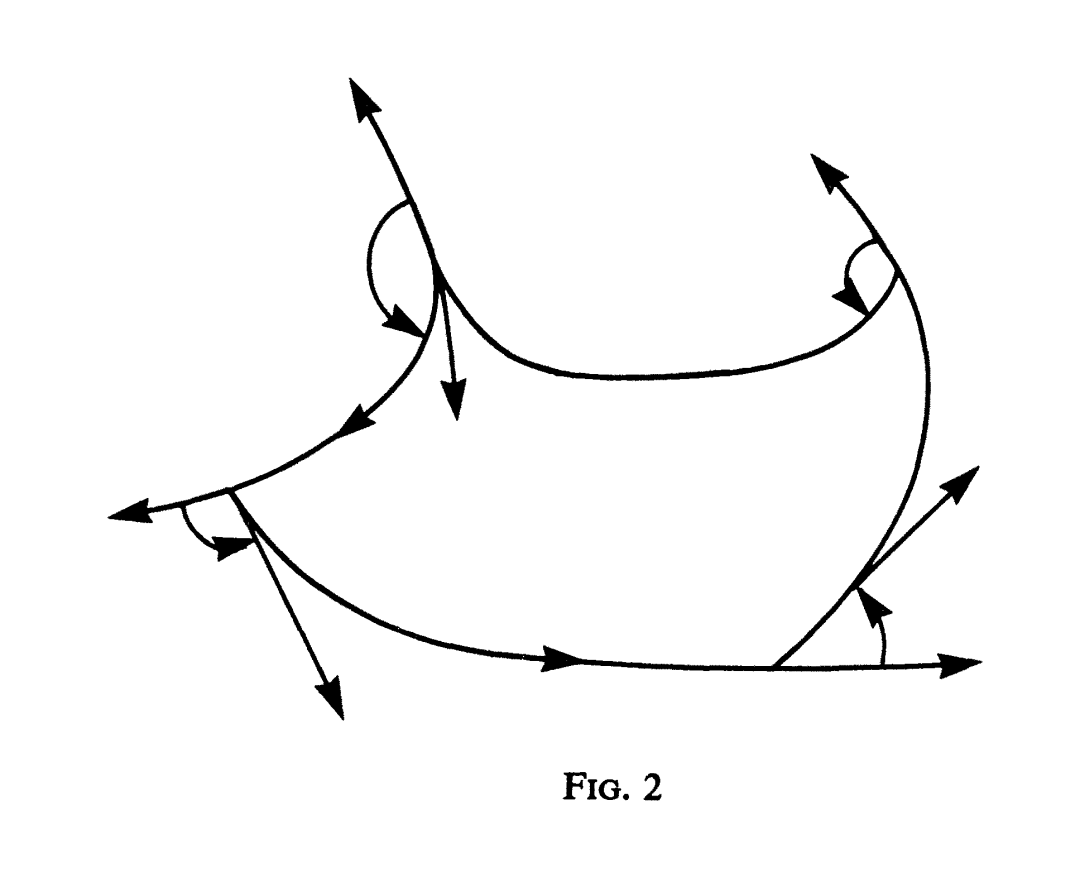
很明显,应该有一个定理把 $n$ 角形外角和定理与简单封闭光滑曲线的旋转指数定理统一起来。要解决这个问题,就要考虑范围更广的一类简单封闭分段光滑曲线。计算这种曲线的旋转指数时,很自然地要规定切线在每个角点处旋转的角度等于该点处的外角(图 2) 。这样,上面的旋转指数定理对这种曲线也成立。应用于 $n$ 角形这一特殊情形,就得到 $n$ 角形外角和等于 $2\pi$(从几何上说曲线转一圈)这个结论。
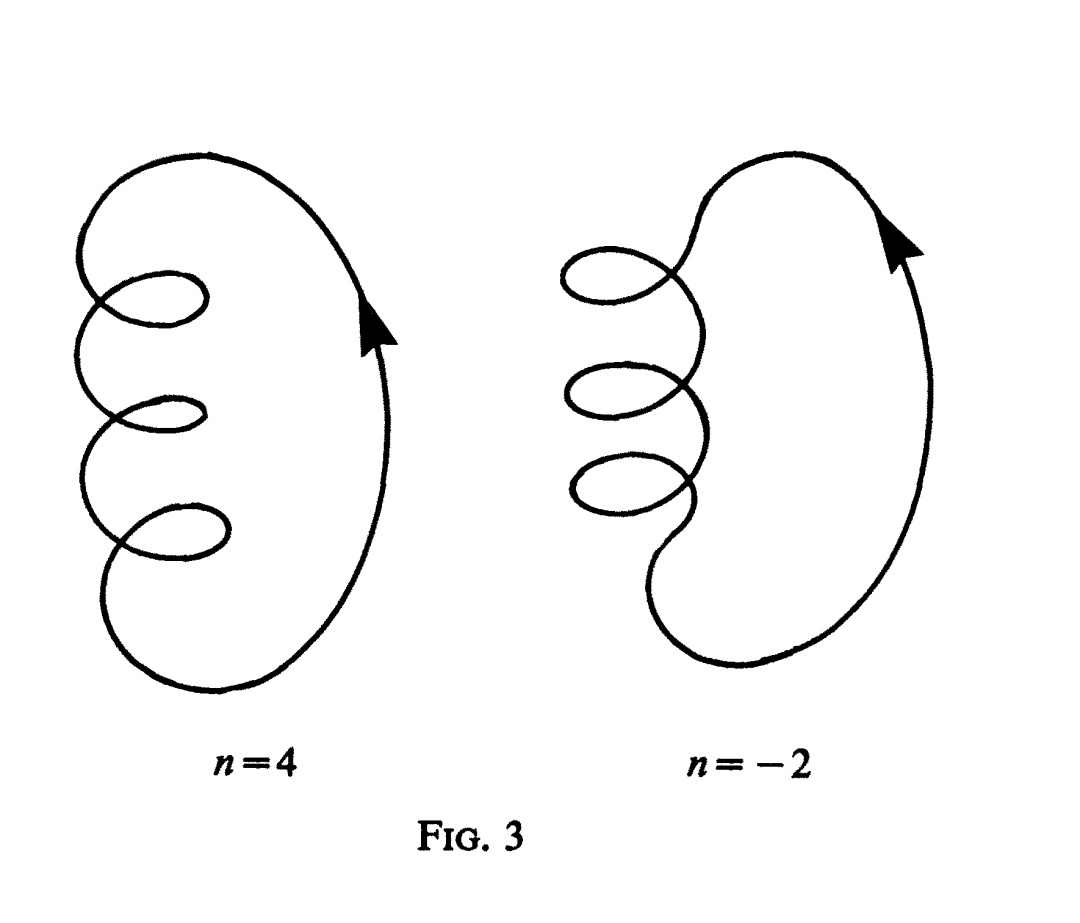
这个定理还可进一步推广到自身有交叉点的曲线。对一个常规的(generic)交叉点,可规定一个正负号。于是,如果曲线已适当地定向,它的旋转指数等于1加上交叉点的代数个数。见图3,例如8字形曲线的旋转指数为0。
几何学中乃至数学中的一个基本概念是形变或称同伦。两条闭光滑曲线称为正则同伦的,如果其中一条可通过一族闭光滑曲线变形成另一条的话。因为旋转指数在形变过程中是连续变化的,而它又是整数,所以一定保持不变。这就是说,正则同伦的曲线具有相同的旋转指数。著名的格劳斯坦——惠特尼定理[5]说,上述命题的逆命题也成立,即:
具有相同旋转指数的闭光滑曲线一定是正则同伦的。
这里,在研究平面上的闭光滑曲线时用了数学中的一个典型手法,就是考察全部这样的曲线,并把它们加以分类。此处就是正则同伦类。这种手法在实验科学中是行不通的,因此它是理论科学和实验科学方法论上一个根本性的差别。
格劳斯坦——惠特尼定理表明,旋转指数是正则同伦类的唯一不变量。
四、三维欧氏几何
现在,从平面转向有着更加丰富内容和不同特色的三维欧氏空间。在空间曲线中(除平面曲线外),最美妙的也许要算圆柱螺旋线了。它的曲率、挠率都是常量,并且它是唯一的能够以一维运动群为自同构的曲线。圆柱螺旋线可按挠率的正负分成右手螺旋线和左手螺旋线两类,它们有本质的区别。见图4。
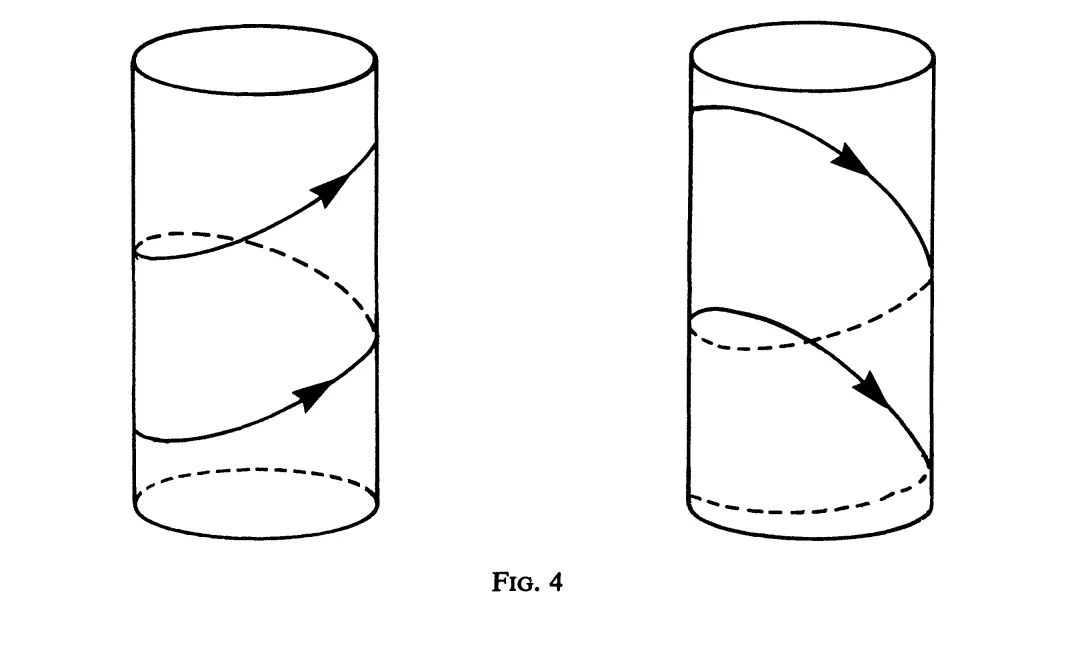
一条右手螺旋线是不可能与一条左手螺旋线经过旋转而全等,除非用镜面反射。螺旋线在力学中起了重要的作用。DNA分子的克里克——沃森模型是双螺旋线,从几何学的观点来看,这也许并非纯属巧合。双螺旋线有一些有趣的几何性质。特别是,如果用线段或弧段分别把两条螺线的两端连接起来,就得到两条闭曲线,它们在三维空间中有一个环绕数$L$(图5)。
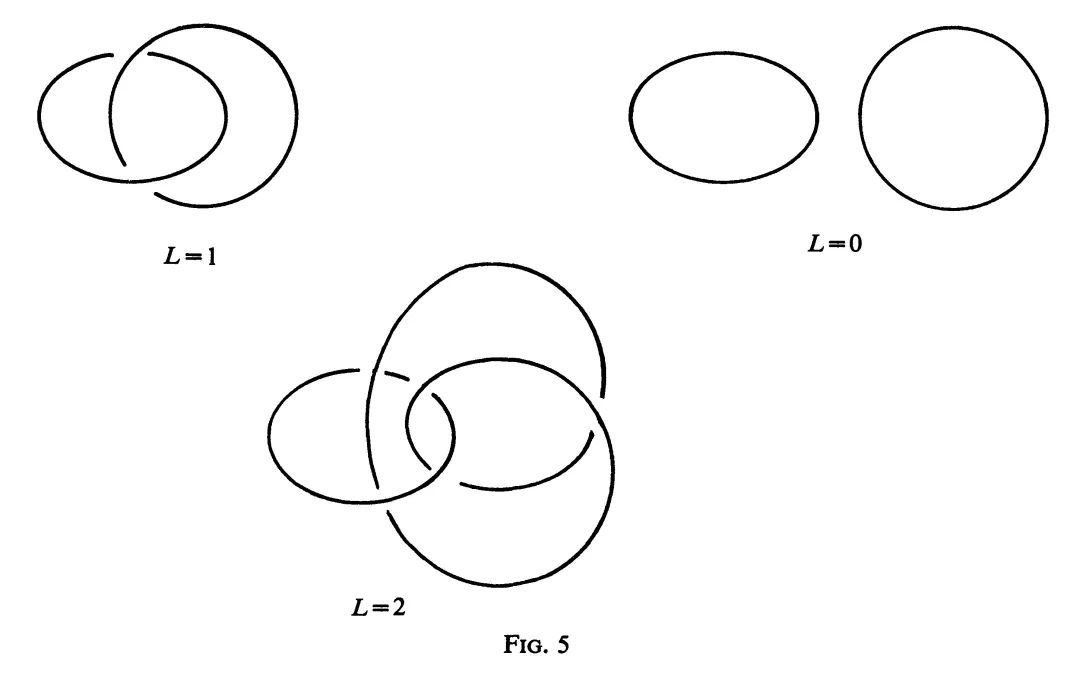
最近在生物化学中,由波尔(W.Pohl)和罗伯茨(G.Roberts)提出一个有争论的问题,即染色体的DNA分子是不是双螺旋线的?如果是这样,那么它就有两条闭线,它们的环绕数是10的5次方量级的。分子的复制过程是:分开这两条闭线,并且把每一条闭线补上它在分子中的补充线(即相补的线)。由于环绕数这么大,波尔和罗伯茨表明,从数学上看,复制过程会有严重的困难。因此(至少对于染色体而言),分子的这种双螺旋线构造是受到怀疑的[6](1979年1月26日补充:近来的一些实验表明,DNA分子的双螺旋结构的一些数学困难,可以通过酶的活动而克服(参见F.H.C.Crick,Is DNA really a double helix? preprint,1978)。环绕数L可由怀特(J.H.White)公式[7]
$$T+W=L \tag{1}$$
决定,这里 $T$ 是全挠率,$W$ 是拧数。后者可用实验来测定,并且在酶的作用下会变化。这个公式是分子生物学中一个重要的基本公式。
DNA分子一般是很长的。为了要把它们放到不大的空间中,最经济的办法是拧它们,使它们卷起来。上面的讨论可能启示着一门新科学——随机几何学——正在诞生,它的主要例子来自生物学。
在三维空间中,比起曲线来,曲面有重要得多的性质。1827年高斯的论文《曲面的一般研究》,标志着微分几何的诞生。它提高了微分几何的地位,把原来只是微积分的一章提高成一门独立的科学。其主要思想是:曲面上有内蕴几何,它仅仅由曲面上弧长的度量决定。从弧长元素出发,可规定其他几何概念,如两条曲线的夹角和曲面片的面积等。于是平面几何得以推广到任何曲面上,这曲面只以弧长元素的局部性质为基础。几何的这种局部化是既有开创性又有革命性的。在曲面上,相当于平面几何中的直线的,是测地线,就是(足够靠近的)两点之间的“最短”曲线。更进一步说,曲面上的曲线有“测地曲率”,这是平面曲线的曲率的推广。测地线就是测地曲率处处为0的曲线。
设曲面求$\Sigma$是光滑的,并取了定向。于是在$Sigma$的每一点$p$,有一个单位法向量$v(p)$,它垂直于$Sigma$在$p$点的切平面(图6)。
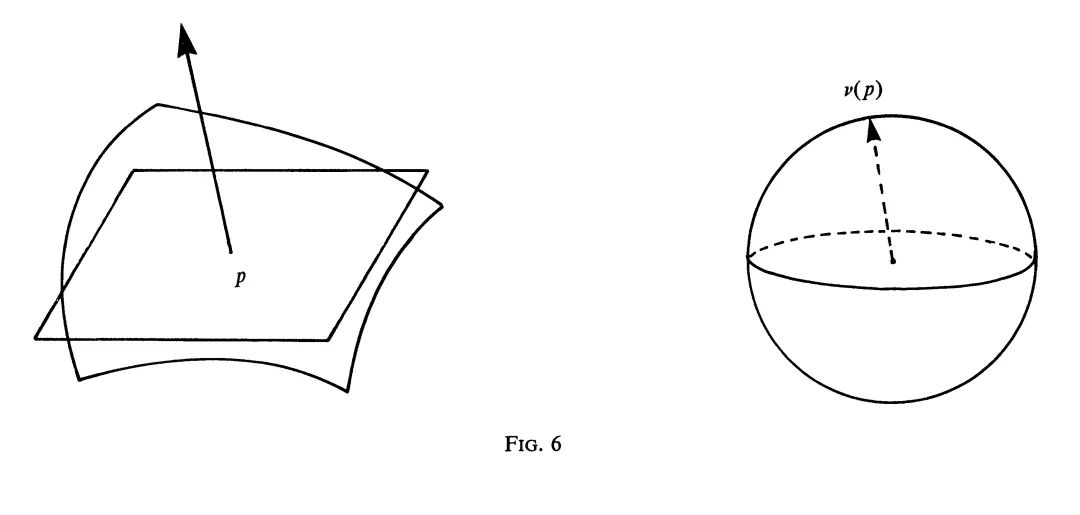
$v(p)$ 可看作以原点为球心的单位球面 $S$ 上一点,从 $p$ 到 $v(p)$ 的映射,即可视为高斯映射:
$$g:\Sigma \rightarrow { S }\tag{2}$$在该映射下,$S$面积元与相应的$\Sigma$的面积元之比值,叫做高斯曲率。高斯绝妙定理说,曲面$\Sigma$的高斯曲率仅仅依赖于$\Sigma$的内蕴几何。而且事实上,在某种意义下,高斯曲率刻划了这个几何。显然,平面的高斯曲率是 $0$ 。如同平面几何中那样,我们在求和上考虑一个由一条或几条分段光滑曲线所围成的区域 $D$ 。 $D$ 有一个重要的拓扑不变量
$$\chi ( D )$$
称做 $D$ 的欧拉示性数。它可以很容易地下定义。用“适当”的方法将 $D$ 分割成一些多角形,以 $v$ , $e$ , $f$ 分别表示顶点、边以及面片的数目,
$$\chi ( D ) = v - e + f\tag{3}$$
(虽然早在欧拉之前就有人知道这个欧拉多面体定理,但似乎欧拉是第一个认识公式(3)中这个“交错和”的重要意义的人。)
在曲面论中,高斯—博内公式是:
$\sum_{\text{顶点}}\text{顶点外的角} + \int _ { \partial D }\text{测地曲率} + \int _ { \partial D } + \iint _ { D } \text{高斯曲率}= 2 \pi \chi ( D ).$如果 $D$ 是一个平面区域,高斯曲率就为 $0$ ,如果它还是单连通的;就有
$$\chi ( D )=1$$在这种情况下,上式就简化成第三节中讨论过的旋转指数定理。从第二节中的三角形的内角和出发,现在我们走得何其远呀!
我们推广闭平面曲线的几何,考虑的空间中闭定向曲面。旋转指数的推广,是公式(2)中的高斯映射$g$的映射度$d$。$d$的确切意义是深刻的。直观地说,它是映射下的象$g(\Sigma)$覆盖单位球面S的代数次数。
在平面上,旋转指数可以是任何整数,而d则不同,它是由曲面$\Sigma$的拓扑所完全决定了的:
对于嵌入空间中的单位球面(即$\Sigma$为单位球面的情况),其映射度$d$等于$1$,它与球面的定向无关。斯梅尔(S.Smale)[8]得到了一个惊人的结果:两个相反定向的单位球面是正则同伦的。说得形象一点:可以通过正则同伦把单位球面从内向外翻过来。在曲面的正则同伦过程中,必须保持曲面在每一点处都有切平面,但允许自身相交。
五、从坐标空间到流形
17世纪,笛卡尔引进了坐标,引发了几何学的革命。用外尔(H.Weyl)[9]的话来说,
“以坐标的形式把数引进几何学,是一种暴力行为。 ”
按他的意思,从此图形和数就会如同天使和魔鬼那样争夺每个几何学家的灵魂。在平面上,一点的笛卡尔坐标$(x,y)$,两个分量是它到两条互相垂直的固定直线(坐标轴)的代数距离。
一条直线是其坐标满足线性方程$ax+by+c=0$的点的轨迹。这样产生的后果是从几何到代数的转化。解析几何的大门一旦敞开,别的坐标系也就纷纷上场。其中有平面上的极坐标,空间的球坐标、柱坐标,以及平面和空间的椭圆坐标。后者适用于共焦的二次曲面的研究,特别是椭球的研究。地球就是一个椭球。
还需要有更高维数的坐标空间。虽然我们原来只习惯于三维空间,但相对论要求把时间作为第四维。而描写质点的运动状态(位置和速度)则需要六个坐标(速矢端线),这是一个比较初等的例子。全体一元连续函数组成一个无穷维空伺,其中平方可积的函数构成一个希尔伯特空间,它有可数个坐标。在这里我们考察具有规定性质的函数的全体,这种处理问题的手法在数学中是基本的。
由于坐标系的大最出现,自然地需要有一个关于坐标的理论。一般的坐标只需要能够把坐标与点等同起来,即坐标与点之间存在一一对应,至于它是怎么来的,有什么意义,这些都不是本质的。
如果你觉得接受一般的坐标概念有困难,那么你有一个好队友。爱因斯坦从发表狭义相对论(1908年)到发表广义相对论(1915年)花了七年时间。他对延迟这么久的解释是[10]:
“ 为什么建立广义相对论又用了七年时间呢?主要原因是,要摆脱‘坐标必须有直接的度且意义’这个旧概念是不容易的。”
在几何学研究中有了坐标这个工具之后,我们现在希望摆脱它的束缚。这引出了流形这一重要概念。一个流形在局部上可用坐标刻划,但这个坐标系是可以任意变换的。换句话说,流形是一个具有可变的或相对的坐标(相对性原则)的空间。或许我可以用人类穿着衣服来做个比喻。“人开始穿着衣服”是一件极端重要的历史事件。“人会改换衣服”的能力也有着同样重要的意义。如果把几何看作人体,坐标看作衣服,那么可以像下面这样描写几何学的进化史:
| 综合几何 | 裸体人 |
| 坐标几何 | 原始人 |
| 流形 | 现代人 |
即使对于数学家来说,流形这个概念也是不简单的。例如,阿达玛(Hadamard)这样一位大数学家,在讲到以流形这概念为基础的李群理论时就说[11]:
“要想对李群理论保持着不只是初等肤浅、而是更深入的理解,感到有着不可克服的困难。”
六、流形:局部工具
在流形的研究中,由于坐标几乎已失去意义,就需要一些新的工具。主要的工具是不变量。不变量分两类:局部的和整体的。前者是局部坐标变换之下的不变量,后者是流形的整体不变量,如拓扑不变量。外微分运算和里奇(Ricci)张量分析是两个最重要的局部工具。
外微分形式是多重积分的被积式。例如在 $x$, $y$, $z$ 空间上的积分
的被积式
$$\iint _ { D } P d y d z + Q d z d x + R d x d y$$
这里$D$是一个二维区域,$P$,$Q$,$R$是$x$,$y$,$z$的函数。人们发现,如果上面的微分的乘法是反对称的,也就是
$$ { d } y \wedge { d } x = - { d } x \wedge { d } y , \cdots$$
这里记号$\wedge$表示外乘,那么$D$(设已有了定向)中变量的变换就会自动地被照顾到了。
更有启发性的办法,是引进二次的外微分形式
$$\omega = P d y \wedge d z + Q d z \wedge d x + R d x \wedge d y$$
并且把积分式写成为积分区$D$与被积式所组成的配对:
$$\iint _ { D } P d y \wedge d z + Q d z \wedge d x + R d x \wedge d y = ( D , \omega )$$因为,假如在$n$维空间中也如此照办,斯托克斯定理就可写成为
$$( D , d \omega ) = ( \partial D , \omega )\tag{10}$$这里$D$是$r$维区域,$\partial D$是$D$的边界,$\omega$是$r-1$次外微分形式,$d\omega$是的外微分,它是$r$次形式。
公式(10)是多元微积分的基本公式,它说明,$d$与$\partial$是伴随算子。值得注意的是,边界算子$\partial$在区域上是整体性的,而外微分算子$d$作用在微分形式上是局部的。
这个事实使得$d$成为一个强有力的工具。$d$作用在函数($0$次形式)和$1$次形式上,分别得到梯度和旋度。
一个微分流形的全部次数小于或等于流形的维数的光滑形式组成一个环,它具有这个外微分算子$d$。嘉当在应用外微分运算到微分几何的局部问题和偏微分方程方面最有成效。在庞加莱的开创工作的基础上,德·拉姆(de Rham)建立了整体理论。这些工作我们将在下一节里讨论。
尽管外微分运算很重要,但它对于描绘流形上的几何和分析特性却是不够用的。一个更广的概念是里奇张量分析。
张量基于这样的事实。一个光滑流形在每一点都可用一个线性空间——切空间——来逼近。一点处的切空间引导到相伴的张量空间。张量场需要有一个附加结构——仿射联络——才能微分。如果流形具有黎曼结构或洛伦茨结构,那么相应的列维—齐维他(Levi-Civita)联络就适用了。
七、同调
在历史上,流形的整体不变量的系统研究是从组合拓扑学开始的。它的想法是把流形剖分(剖分要满足一定要求,我们不细说了)些成一些胞腔,研究它们是如何装拼在一起的。
特别当$M$是一个$n$维闭流形时,设$a_k$是$k$维胞腔的个数,$k=0,1,\cdots,n,那么作为公式(3)的推广,$M$的欧拉—庞加莱示性数可定义为
$$\chi ( M ) = a _ { 0 } - a _ { 1 } + \cdots + ( - 1 ) ^ { n } a _ { n }.\tag{11}$$
边缘是同调论中的基本概念。胞腔的整系数线性组合称为一个链。如果一个链没有边缘(边缘为0),则称作闭链。链的边缘是闭链(图7)。
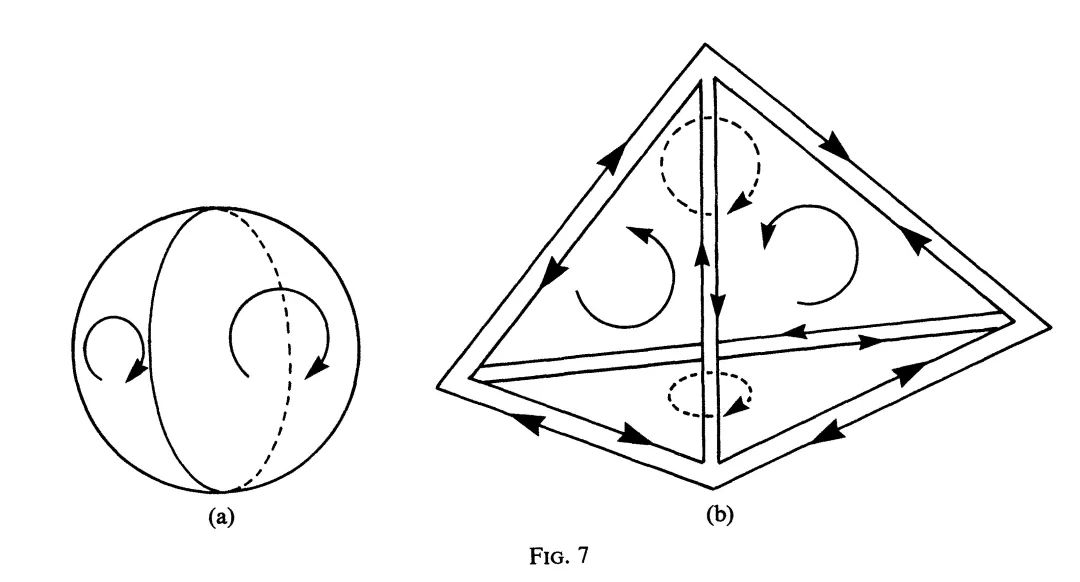
在模k维边缘链的意义下,线性无关的k维闭链的个数称为M的k维贝蒂数,记作b_k,它是一个整数。欧拉—庞加莱公式说
$$\chi ( M ) = b _ { 0 } - b _ { 1 } + \cdots + ( - 1 ) ^ { n } b _ { n }\tag{12}$$贝蒂数是M的拓扑不变量,因此欧拉数也是拓扑不变量。换言之,贝蒂数与欧拉数都是与剖分的方式无关的,并且在M的拓扑变换下保持不变。这些,以及更一般的叙述,可以看作是组合拓扑学的基本定理。
庞加莱和布劳威尔(L. E. J. Brouwer)为组合拓扑学的发展开辟了道路。以维布伦、亚历山大(Alexander)和莱夫谢茨(Lefschetz) 等为首的美国数学家的工作使得它于本世纪二十年代在美国开花结果。剖分的方法虽然是导出拓扑不变量的一个有效途径,但它也有“杀死”流形的危险。明确地说,组合的方法可能使我们看不出拓扑不变量和局部几何性质的关系。实际存在着与同调论相对偶的上同调论。同调论依赖于边缘算子$\partial$,而上同调论立足于外微分算子$d$,它是一个局部算子。从$d$发展出的德•拉姆上同调论可概括如下:
算子$d$有一个基本性质:重复运用它时得到$0$次形式。也就是说,对任何$k$次形式$\alpha$,$(k+1)$次形式$d\alpha$的外微分是$0$。这相当于“任何链(或区域)的边缘没有边缘。”这样一个几何事实(参见公式(10))。当$d\alpha=0$时,就称$\alpha$是闭的。当存在一个$(k-1)$次形式$\beta$使得$\alpha=d\beta$时,就说$\alpha$是一个恰当形式。恰当形式总是闭的。两个闭形式如果相差一个恰当形式,则说它们是上同调的。互相上同调的闭$k$次形式的全体组成$k$维的上同调类。不平常的是,虽然$k$次形式、闭$k$次形式以及恰当$k$次形式的数量都是极大的,但$k$维上同调类却组成一个有限维的线性空间,而维数就是第$k$个贝蒂数$b_k$。
德·拉姆上同调论是层的上同调的先驱。后者由勒雷(J.Leray)[12]始创,小嘉当(H.Cartan)和塞尔(J.P.Serre)使之完善,并卓有成效地加以应用。
八、向量场及其推广
我们自然地要研究流形$M$上的连续向量场。这样的一个向量场由$M$的每一点处的一个切向量组成,并且向量随着点连续变动。若$M$的欧拉—庞加莱示性数不等于$0$,则$M$上任一连续向量场中至少有一个零向量。举个具体的例子,地球是个二维球面,示性数是$2$,因此当地球上刮风时,至少有一处没有风。对上述结果,有一个更加明确的定理。对于连续向量场的每一个孤立零点可规定一个整数,叫做指数,它在某种程度上刻划向量场在这个零点附近的状态,表明它是源点、汇点还是其他情形.庞加莱—霍普夫(Hopf)定理指出,当连续向量场只有有限多个零点时,它的全部零点的指数和就是拓扑不变量
以上所述是有关$M$的切丛的。切丛就是$M$的全体切空间的集合。更一般地,如果一族向量空问以$M$为参数,并且满足局部乘积条件,就称为$M$上的一个向量丛。
一个基本问题是:这样的丛在整体上是不是一个乘积空间?上面的讨论说明了,当欧拉数不等于0时,切丛不是乘积空间,因为如果是乘积空间,就会存在一个处处不为0的连续向量场。空间之中存在局部是乘积而整体不是乘积这种空间(例如当欧拉数不等于0时的M的切丛)决不是容易想象的,几何学从而进入更深刻的阶段。
刻划一个向量丛与乘积空间的整体偏差的第一组不变量是所谓上同调示性类。欧拉—庞加莱示性数是最简单的示性类。在曲面$\Sigma$没有边界时,高斯—博内公式的形式(见第四节)特别简单
$$\iint _ { \Sigma } K { d } A = 2 \pi \chi ( \Sigma )\tag{4a}$$
这里K是高斯曲率,$dA$是面积元。公式($4a$) 是最重要的公式,因为它把整体不变量欧拉数表示成局部不变量高斯曲率的积分。这也许是局部性质与整体性质之间的最令人满意的关系了。
这个结果有一个推广,设
$$\pi : E \rightarrow M$$是一个向量丛。切向量场的推广是丛的截面,也就是一个光滑映射$s: M→ E$,使
$$\pi \circ S$$
是恒同映射。因为E只是一个局部乘积空间,对截面s微分就需要有一个附加结构,通常叫做一个联络。所导出的微分称为协变微分,一般不是交换的。曲率就是协变微分非交换性的一种度量。曲率的适当组合可得出一类微分形式,在德·拉姆理论的意义下,它代表上同调示性类,而高斯—博内公式(4a) 是它的最简单的例子[13]。
我相信,向量丛、联络和曲率等概念是如此基本而又如此简单,以致任何多元分析的入门教科书都应包括这些概念。
九、椭圆型微分方程
当$n$维流形$M$有黎曼度最时,则有一个算子$*$它把一个$k$次形式$\alpha$变成一个$(n-k)$次形式$*\alpha$。这相当于对切空间的线性子空间取正交补。借助算子$*$和微分$d$,我们引进余微分
$$\delta = ( - 1 ) ^ { n k + n + 1 } * d *\tag{14}$$
和拉普拉斯算子
$$\Delta = { d } \delta + \delta { d }.\tag{15}$$
算子$δ$把一个$k$次形式变成一个$(k-1)$次形式,而 $△$ 把一个$k$次形式变成一个$k$次形式。如果一个形式$\alpha$满
$$\Delta \alpha = 0.$$
它就称为调和的。零次调和形式就是通常的调和函数。
方程(16)是一个二阶椭圆型偏微分方程。如果流形M是闭的,公式(16)的全部解构成一个有限维向量空间。根据霍奇(Hodge)的一个经典定理,解空间的维数恰好是第$k$个贝蒂数$b_k$。再从公式(12) 推出,欧拉示性数可写成
$$\chi ( M ) = d_{\text{偶}}-d_{\text{奇}}$$
其中$d_{\text{偶}}$和的$d_{\text{奇}}$分别是偶次和奇次调和形式的空间的维数。外微分$d$本身是一个椭圆算子,上述公式可看作是用椭圆算子的指标来表示$M$的欧拉数。对于任何线性椭圆算子来说,其指标定义为解空间的维数减去伴随算子的解空间的维数。
在用局部不变量的积分表示椭圆算子的指标这一方面,阿蒂亚—辛格(Atiyah-Singer)指标定理达到了顶峰。许多著名的定理,例如霍奇指标定理、(Hirzebruch)指标定理和关于复流形的黎曼—洛赫定理,都是它的特殊情形。这项研究的一个主要副产物,是确认了考虑流形上伪微分算子的必要性,它是比微分算子更一般的算子。
椭圆型微分方程和方程组是与几何十分紧密地纠缠着的。一个或多个复变量的柯西—黎曼微分方程是复几何的基础。极小流形是求极小化面积的变分法问题中欧拉—拉格朗日方程的解。这些方程是拟线性的。“最”非线性的方程也许是蒙日—安培方程,它在好几个几何问题中都是重要的。近年来在这些领域里取得了很大的进展[14]。
由于分析这样深入地渗透到几何,前面提到过的分析学家伯克霍夫的评论看来更令人不安了。然而,分析学是绘制矿藏的全貌,而几何学是寻找美丽的矿石的。几何学建筑在这样的原则上:并非所有的结构都是相等的,并非所有的方程都是相等的。
十、欧拉示性数是整体不变量的源泉
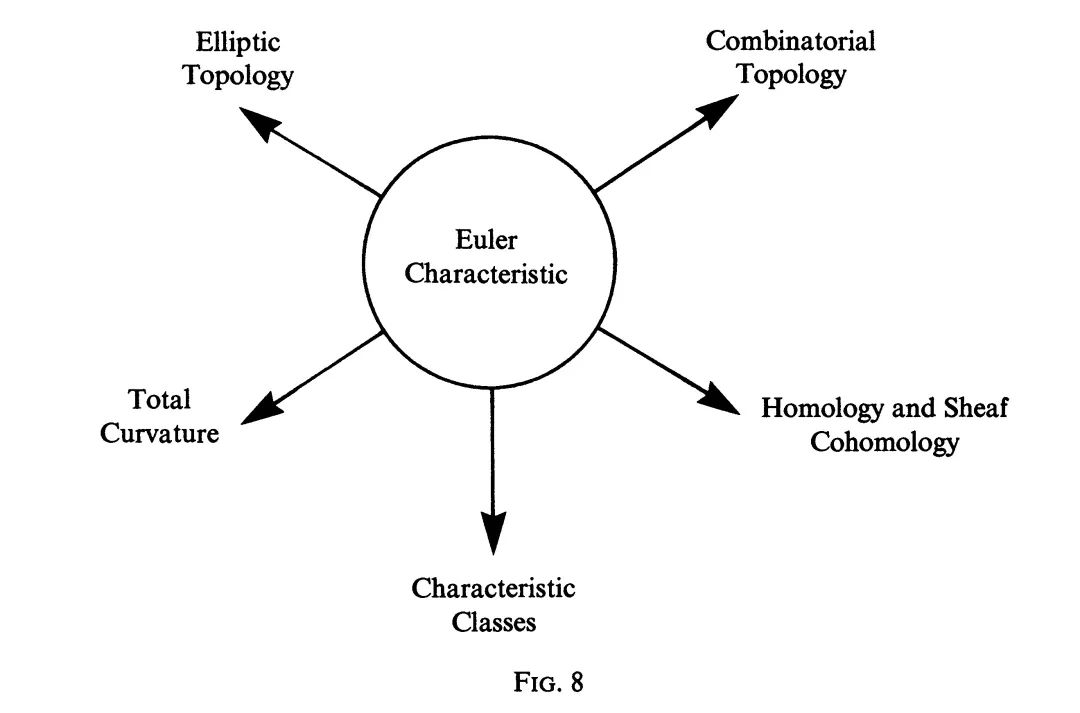
概括起来,欧拉示性数是许多几何课题的源泉和出发点。我想用下面的图8来表示这关系。
十一、规范场论
本世纪初,由于爱因斯坦的相对论,微分几何一度变成人们注视的中心。爱因斯坦企图把物理现象解释为几何现象,并构造一个适合于物理世界的几何空间。这是一个十分艰巨的任务,也不清楚爱因斯坦关于引力场和电磁场的统一场论的学说是否已成为定论。前面提到过的向量丛的引进,特别是向量丛中的联络和它们的示性类,以及它们与曲率的关系,开阔了几何的视野。复线丛(纤维是一条复直线)的情况提供了外尔的电磁场规范理论的数学基础。以对同位旋的理解为基础的杨—米尔斯理论,是非交换的规范理论的第一个例子。
杨—米尔斯理论的几何基础,是带有酉联络的复平面丛。近来,统一所有的场论(包括强、弱相互作用)的尝试,已集中到一个规范理论上,也就是一个以丛和联络为基础的几何模型。看到几何和物理再次携起手来,是十分令人满意的。丛、联络、上同调和示性类都是艰深的概念,在几何学中它们都经过长期的探索和试验才定形下来。物理学家杨振宁说[15]:
“非交换的规范场与纤维丛这个美妙理论——数学家发展它时并没有提及物理世界——在概念上的一致,对我来说是一大奇迹。 ”
1975年他对我讲:
“这既是使人震惊的,又是使人迷惑不解的,因为你们数学家是没有依据地虚构出这些概念来的。 ”
这种迷惑是双方都有的。事实上,维格纳(E. Wigner)说起数学在物理中的作用时,曾谈到数学的超乎常理的有效性[16]。如果一定要找一个理由的话,那么也许可用“科学的整体性” 这个含糊的词儿来表达。基本的概念总是很少的。
十二、结束语
现代微分几何是一门年青的学科。即使不考虑相对论和拓扑学给它的很大促进,它的发展也一直是连续不断的。我为我们说不清它是什么而高兴。我希望它不要象其他一些数学分支那样被公理化。保持着它跟数学中别的分支以及其他科学的许多领域的联系,保持着它把局部和整体相结合的精神,它在今后长时期中仍将是一片肥沃的疆域。
用函数的自变数的数目或数学所处理的空间的维数来刻划数学的各个时期,可能是很有意思的事。在这个意义上,19世纪的数学是一维的,而20世纪的数学是n维的。由于多维,代数获得了十分重要的地位。所有已知流形上的整体结果的极大多数是同偶数维相关的。特别地,所有复代数流形都是偶数维实流形。奇数维流形至今还是神秘的。我大胆地希望,它们在21世纪将受到更多的注意,并可在本质上被搞清楚。近来,瑟斯顿(Thurston)[17]关于三维双曲流形的工作以及丘成桐、米克斯(Meeks)和舍恩(Schoen)关于三维流形的闭极小曲面的工作,都已经大大地弄清楚了三维流形及其几何。几何学中的问题之首可能仍然是所谓庞加莱猜想:一个单连通三维闭流形同胚于三维球面。拓扑和代数的方法至今都还没有导致这个问题的解决。可以相信,几何和分析中的工具将被发现是很有用处的。
参考文献
O. Veblen and J. H. C. Whitehead, Foundations of Differential Geometry, Cambridge, England, 1932, p. 17.
Elie Cartan, Le rôle de la théorie des groupes de Lie dans l’évolution de la géométrie moderne, Congrès Inter. Math., Oslo, 1936, Tome I, p. 96.
George D. Birkhoff, Fifty years of American mathematics, Semicentennial Addresses of Amer. Math. Soc., 1938, p. 307.
A. Weil, S. S. Chern as friend and geometer, Chern, Selected Papers, Springer Verlag, New York, 1978, p. xii.
H. Whitney, On regular closed curves in the plane, Comp. Math. 4 (1937) 276-284.
William F. Pohl and George W. Roberts, Topological considerations in the theory of replication of DNA, Journal of Mathematical Biology, 6 (1978) 383-386, 402.
James H. White, Self-linking and the Gauss integral in higher dimensions, American J. of Math., 91 (1969), 693-728; B. Fuller, The writhing number of a space curve, Proc. Nat. Acad. Sci., 68 (1971) 815-819; F. Crick, Linking numbers and nucleosomes, Proc. Nat. Acad. Sci., 73 (1976) 2639-2643.
S. Smale, A classification of immersions of the two-sphere, Transactions AMS, 90 (1959) 281-290; cf. also A. Phillips, Turning a surface inside out, Scientific American, 214 (May 1966) 112-120. A film of the process, by N. L. Max, is distributed by Intermational Film Bureau, Chicago, Ill.
H. Weyl, Philosophy of Mathematics and Science, 1949, p. 90.
A. Einstein, Library of Living Philosophers, vol. 1, p. 67.
J. Hadamard, Psychology of Invention in the Mathematical Field, Princeton, 1945, p. 115.
R. Godement, Topologie algébrique et theorie des faisceaux, Hermann, Paris, 1958.
S. Chern, Geometry of characteristic classes, Proc. 13th Biennial Sem. Canadian Math. Congress, 1-40 (1972).
S. T. Yau, The role of partial differential equations in differential geometry, Int. Congress of Math., Helsinki, 1978.
C. N. Yang, Magnetic monopoles, fiber bundles, and gauge fields, Annals of the New York Academy of Sciences, 294 (1977) 86-97.
E. Wigner, The unreasonable effectiveness of mathematics in the natural sciences, Communications on Pure and Applied Math., 13 (1960) 1-14.
W. Thurston, Geometry and topology in dimension three, Int. Congress of Math., Helsinki, 1978




