我曾告诉一个友人，我用数学尝试去了解偏头痛。她以为我请偏头痛患者做心算，以减轻他们的症状。这当然不是，我真正做的是运用数学理解偏头痛的生物学原因。

生活中我们往往忽略的一个重要事实是：数学可以理解世界。你可能会提醒我：这一事实并不明显。在这篇文章中，我要讨论一个大问题：“为什么数学可以用来描述世界”，或更挑衅般地延伸为“为什么应用数学如此强大？”要做到这一点，我们需要回顾一般数学哲学---大体上称为元数学---的悠久历史。

什么是应用数学

令人惊奇的事实：世界能由数学理解

在进一步阐述之前，我们应该清楚应用数学意指什么。我将借用一下20世纪和21世纪的一个重要应用数学家、剑桥大学的流体力学G.I.泰勒（G.I.Taylor）讲座教授Tim Pedley给出的定义。他在数学与应用研究所2004年的就职演说中指出：“应用数学是指用数学的技术，对非数学领域提出的问题给出答案。”这个定义是相当广泛的，包括从数值变化到气候变化，正是这种广泛定义的可能性是我们将要讨论的奥秘中的一部分。

为什么应用数学非常实用？这个问题比其他任何你可能会问的有关数学的本质的问题更重要。首先，由于应用数学是数学，它会引发传统上对元数学所产生的所有的同样问题。其次，作为应用，它在科学哲学上必然会提出一些需要讨论的问题。这个情况可以被视为我们的一个大问题，事实上它也是科学和数学哲学的大问题。讨论这些问题之前，让我们先转向元数学的历史：数学、它的本质及适用性已经被了解了多少？

元数学

雅典学派的柏拉图和亚里士多德

历史上的数学一般没有纯粹和应用数学之间的区别。然而，近代数学在过去的两个世纪中出现了纯数学几乎独占鳌头的局面，尤其在强调了所谓的数学基础---即使数学命题为真的东西是什么？对基础感兴趣的元数学家们通常分为四大阵营：

• 形式主义者，如大卫·希尔伯特，他们认为数学基于集合论和逻辑的组合，并在一定程度上把做数学的过程视为根据某些既定规则所作的本质上毫无意义的符号洗牌。
• 逻辑主义者把数学看着是逻辑的延伸。著名的逻辑主义代表人物伯特兰·罗素和阿尔弗雷德·怀特海花了数百页的篇幅，以（从逻辑上）证明一加一等于二。
• 直觉主义者的响当当人物是L.E.J.布劳威尔，有人这样评价他说：“他不会相信是否在下雨，直到他看到窗外以后”（根据Donald Knuth）。这句话讽刺直觉主义者的中心思想：拒绝排中律。这普遍接受的定律说：一个命题（如“下雨”）或真或假，即使我们还不知道它到底是真是假。相反，直觉主义者认为除非你已经完全证明了该命题或构造了反例，它没有客观的真实性。此外，直觉主义者对他们能接受的无穷符号给出严格限制。他们相信数学完全是人类心智的产物，并且他们规定数学仅能把无穷用于1-2-3类型过程的算术延伸。结果，他们在证明中仅仅允许可数的运算，即能由自然数描述的运算。
• 最后，作为这四个阵营的最老成员，柏拉图主义者相信外部的现实，以及数很数学之外其他事物的存在。对于像哥德尔(Kurt Godel)这样的柏拉图主义者，数学存在于人类心智之外，也可能在物理世界之外，但是在人类的心智世界和数学的柏拉图王国之间有一种神秘的联系。

人们争论着这四种流派的哪一个---如果有的话---可以充当数学的基础。好像这些被纯化的讨论与应用问题毫无关系，但也有说法认为这种关于基础的不确定性恰恰影响了数学的应用。在《确定性的消失》(The Loss of Certainty)这本书中，克莱因(Morris Kline)在1980年写道：“关于什么是健全的数学的危机和冲突也已经阻碍了数学方法论在哲学、政治学、伦理学、美学等文化领域中的应用[...]理性时代已经一去不复返了。”令人感激的是，数学现在开始用于这些领域，但是我们已经学到一个重要的历史教训：对于数学应用的选择，有一个敏感于元数学问题的社会学维度。

数学基础与数学可适用性

世界是数学的，还是人类心智的构建？

思考数学适用性的元数学家合乎逻辑的下一步是问：关于我们的大问题，关于数学基础的这四大学派观念中的每一个将断言什么？关于这方面的讨论已出现在一些数学家和科学家的著作中，如彭罗斯(Roger Penrose)的著作《现实之路》(The Road to Reality)或戴维斯(Paul Davies)的著作《上帝的思考》(The Mind of God)。

我将通过倒转“合乎逻辑”的下一步来走另一条路：我想问“对数学的可适用性而言数学基础必须说些什么？”在问这一问题时，我先假定数学有用这个命题是没人反对的，现代科技极端依赖数学的众多例子已见证了这个事实。

那么一个形式主义者怎么解释数学的可适用性呢？如果数学真的除了是世界上这个历时最长、玩家最多的游戏中的数学符号洗牌之外，别无他物的话，那么它谈何去描绘世界？数学游戏有什么特权比其他游戏更能描绘世界？记住，该形式主义者必须在形式主义者的世界观里回答问题，故不允许诉诸柏拉图之类的数学更深层意义或与物理世界深藏不露的联系。由于类似的理由，逻辑主义者也挣扎不已，因为如果他们说：“嗯，也许世界是逻辑的体现”，那么他们悄然地假设能被体现的逻辑柏拉图王国的存在性。这就把逻辑主义置为柏拉图主义的一个分支，如我们下面要看到的，它将出现它自己的重大问题。因而对于形式主义者和非柏拉图主义的逻辑主义者而言，应用数学的存在性可以严重挑战他们的地位。

不仅逻辑主义而且形式主义都不再被广泛相信，尽管有这样的陈词滥调：数学家在一周之中是柏拉图主义者，而周末是形式主义者。这两种观念都不再受宠，其理由不是关于数学的可适用性这一潜在的大问题，而是基本上与哥德尔(Godel)、Thoralf Skolem及其他人的工作有关。

第三个的基础直觉主义自始至终就未获得大量支持。如果说它被考虑到的话，大部分时间是被数学家们抱怨地说起。它所提供的高度限制性的证明工具箱和奇怪的不确定符号，以及一个命题非真非假直到一个构造性证明出现为止，让这种观点对许多数学家而言都毫无吸引力。

然而，宇宙中各种过程及可数本质的中心思想似乎可从现实中导出。物理世界，至少我们人类所感知的，似乎由可数多个事物组成，且我们可能遇到的任何无穷性都是延伸一个计数过程后的结果。以这种方式，直觉主义或许来自于自然是至多可数的无穷这一物理世界的现实。直觉主义看上去给予数学的可适用性问题提供了一个优雅的回答：数学是可适用的，因为它来自于现实。

但是，更细的探究会让这个回答土崩瓦解。首先，现代数学物理中有许多东西，比如说量子理论，需要超过可数的无穷概念。单单这点就可能永远超过直觉主义数学的解释能力了。

有一个现代思想可能获益于直觉主义者的有穷论逻辑，即所谓的数字物理。它认为宇宙近似于巨型计算机。例如，基本粒子由它们恰好在某个给定时刻的量子状态描述，就像计算机科学中的比特由它的0或1值所定义一样。宇宙就像一台计算机那样建立在状态信息的基础之上，它的演变从理论上讲可以由巨型计算机模拟。因此有数字物理的座右铭：“它来自比特”。

但是，这个世界观也未能成为真正直觉主义的，它似乎潜入到柏拉图的一些想法之中。信息论的比特看似假定派生出物理世界的信息之柏拉图式存在性。

但更根本的是，直觉主义对非直觉的数学为什么是可应用的问题回答不了。很可能一个非直觉的数学定理有了直觉的证明时才适用于自然世界，但此断言尚未建立。此外，虽然直觉数学看起来好像从现实世界派生而来，但尚不清楚人类心智的对象是否就是需要忠实代表物理宇宙的对象。

建立在数学的形象中

伽利略相信世界是以数学语言书写的。他面对罗马宗教裁判所宣称地球围绕太阳转。

形式主义和逻辑主义都没有回答我们的大问题。关于直觉主义是否能做到的判断也已经作出，但巨大的概念困难依然存在。那么，柏拉图主义能做什么？

柏拉图主义者认为物理世界是数学王国的一个不完善的影子。物理世界在某种程度上出现于这种柏拉图王国中并植根于它，因此世界的对象及其之间的关系是柏拉图王国的对应影子。世界由数学描述的事实不再是一个谜，因为它已成为一个公理：世界扎根于数学王国。

但是更大的问题出现了：为什么物理王国出现并植根于柏拉图王国？为什么精神王国来自物质世界？为什么精神王国与柏拉图王国有某些直接关联？

确实，我们生活在一个神圣的宇宙之中，并通过学习数学和科学来分享神圣的心灵，这一信念已经可以说是理性思维的时间最长的动机，世代相传，从毕达哥拉斯、牛顿，到今天的许多科学家。在这个意义上说，“上帝”似乎在时空世界既非一个对象，也非物理世界中的对象总和，更不是柏拉图世界中的一个元素。相反，上帝是接近柏拉图王国整体的某样东西。在这种方式中，上面所述的柏拉图主义者所面对的很多困难与犹太教和基督教世界神学家所面临的相同。

假如我们认为上面的大问题是有答案的，那么伽利略的“宇宙之书”写于数学“语言”的不朽言论是一种寻求答案的柏拉图式叙述。今天，甚至非宗教的数理学家经常表达探索柏拉图王国时的敬畏之感，认为他们不创造数学，而是发现它。保罗•戴维斯(Paul Davies)在其著作《上帝的思考》(The Mind of God)中走得更远，强调了这种动机的双向性：它不仅可以带动数学家了解数学以便一睹心中之神，而且接近“宇宙的关键”的这一能力给予了我们生存的一些目的或意义。

事实上，假设数学结构及宇宙的物理本质和我们对它们的精神接触是“上帝”的某种心灵、本质及身体的一部分，那么对数学基础及其适用性探讨将有比以上描述的那些学说大得多的一个答案。这样一个假设已在过去几千年中各种各样的宗教、文化和科学系统中发现。然而，让哲学家或科学家全心全意地接受这个观点不是件很自然的事，这样做也许会鼓励保全模糊面纱的神秘性，而不是揭开这个面纱。

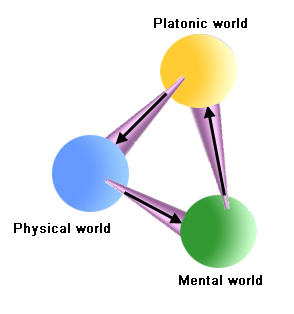Penrose的三位世界图

罗杰•彭罗斯(Roger Penrose)用一个三位世界图清晰地说明了这个奥秘。柏拉图的、物理的和精神的世界是问题中的三个对象，他把它们勾勒为排成三角形的三只球。一个锥体连接柏拉图世界与物理世界：在最常见的形式下，该图显示锥体窄的那端穿透柏拉图世界，而宽的那端则渗透到物理世界。这至少部分表明物理世界嵌入在至少一些柏拉图世界当中。一个类似的锥体连接物理世界与精神世界，至少部分的精神世界嵌入在物理世界之中。最后，也是最神秘的，三角形以一个把精神世界连接到柏拉图世界的锥体完成：柏拉图世界至少部分地嵌入到精神世界。每个锥体和每个世界本身，仍是一个谜。

我们似乎已经陷入相当令人沮丧的僵局中，关于数学基础的四个论点中没有哪个可以毫不含糊地回答数学的可适用性问题。不过，我希望你读完这篇文章研究后的感觉是：这是令人难以置信的好消息！梳理出应用数学为什么存在这一大问题的细微之处，是未来的一个项目，这个项目于探讨数学、物理宇宙及我们在这两个有意义的系统中所处位置的本质方面，可能产生深刻的洞察。