译文
万物源于量子比特?——数学物理界“教皇”关于量子理论的深思

威滕的研究工作极大地推动了理论物理近几十年的发展,其中最为人熟知的应该就是神秘的M理论。自爱因斯坦以来,杰出的物理学家们一直都在寻找一种更加基本的量子理论,来统一引力与其他基本力,并取代爱因斯坦关于“引力的本质是时空弯曲“(也就是广义相对论)的近似图象。
直觉主义数学

如果你发现很难坚持自己的原则生活,请想想 20 世纪初数学家 Luitzen Egbertus Jan Brouwer 面临的困境。Brouwer 觉得自己不同意数学研究的方式。为了准确,许多数学都必须重新书写。保持沉默很容易,但 Brouwer 却宁愿接受挑战。
几何音乐理论
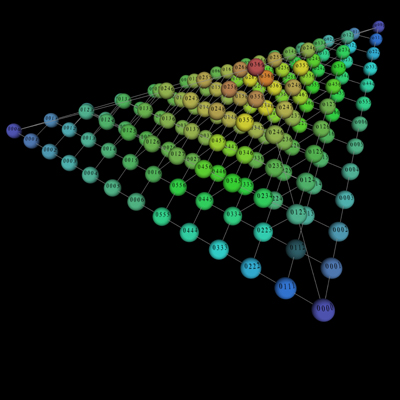
几何音乐理论中的四音符和弦 - 音符集合形成一个四面体,颜色表示一个序列中各个音符之间的间距。在蓝色球体中,音符是群集的;在较暖的颜色中,它们之间的距离更远。金字塔顶端的红球是第七和弦的缩减。其附近都是西方音乐中最熟悉的和弦。
“科学家的床头柜”之大卫·芒福德篇

David Mumford:布朗大学应用数学系荣誉退休教授,主要研究代数几何、视觉和模式理论(vision and pattern theory). Mumford教授1961年在哈佛大学毕业,博士论文题为 Existence of the moduli scheme for curves of any genus. 1974年得菲尔兹奖,2006年与吴文俊院士一起获得邵逸夫数学奖,2008年得沃尔夫数学奖. 2002年在北京国际数学家大会上发表题为 Pattern Theory: the Mathematics of Perception 的全会报告. 时至今日,Mumford 教授所写的代数几何教科书仍是每一个学习数学的学生必须参考的经典著作.
什么是双有理几何——2018年菲尔兹奖得主 Caucher Birkar及其工作介绍
Birkar的研究领域是双有理几何,这是专门研究用这种方式分类代数簇的。特别地,数学家期望证明每一个射影代数簇都双有理地联系到某个特殊的好簇,这些好簇是由三种基本组件组成的。对于最简单的(一维复)簇,这已经被19世纪末的数学家黎曼6证实。二维的情形在20世纪初已经搞清楚。随着时间的推移,三维的情形在20世纪70年代到20世纪90年代之间才了解清楚。四维及以上的情形仍然有很多关键问题,而Birkar恰是在这一领域做出了重要贡献。这一领域的目标是证明所谓的极小模型纲领是可行的,这是一种专门设计的将任何代数簇转变为上述三种漂亮的基本组件的算法。
只有八维数字,才能还原宇宙的本质?

对于一维、二维乃至四维的数字,人们都不陌生:一维的实数一直都存在于经典物理中,复数提供了量子物理的数学基础,四元数则是爱因斯坦狭义相对论的基础。然而,最为复杂的数字形态——八元数,又与现实世界存在着怎样的关系呢?
二十世纪的数学
如果有人想谈论一个世纪的终结以及下一个世纪的开始,那么他有两个具有相当难度的选择:一个是回顾过去百年的数学;另一个是对未来百年数学发展的预测,我选择了前面这个比较困难的任务,任何人都可以预测未来而且我们并不能判定是对还是错.然而对过去的任何评述,每个人都可以提出异议.
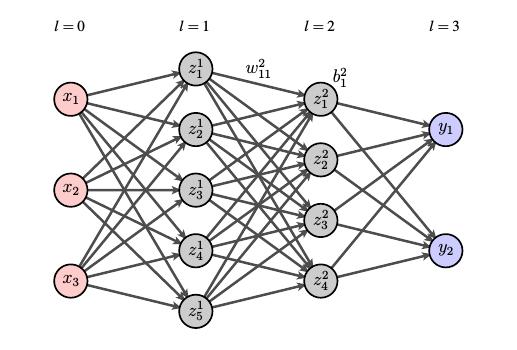
什么是机器学习?
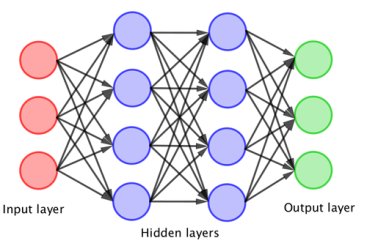
机器学习是最近人工智能领域最重要的发展之一。我们对于智能的想法是,不是把东西教授给机器(在传统计算机程序的意义上),而是机器自己学习的东西,这样它就能直接从做这些的经验(或数据)中学习如何处理复杂的任务。
I. M. Gelfand 自述
Gelfand是20世纪最伟大的数学家之一。据说,在20世纪的俄国,最杰出的数学家有3位,分别是Kolmogorov,Gelfand 和 Shafarevich(前不久去世)。Kolmogorov的工作广,Shafarevich的工作深,而唯有Gelfand,工作既深且广。