神经网络及其学习方法
David Austin/文
杨艳秋 赵泽榕/译
本专栏介绍了神经网络,一种旨在模拟生物神经组织的编程范例,以及提高学习能力的数学理论。
引言
在一些任务上,电脑比我好得多。我不想和电脑赛跑去找反正切 arctan(1.374),如果我需要找到与 “线性代数” 相关的网页,我会请 Google 帮我做。
但是,为了保护我自己的处理单元,我非常擅长其他的事情,比如阅读学生的手稿。例如,我很容易将这些图像识别为表示 0-9 的数字。

事实上,我甚至可以毫不费力地识别出具有不同拓扑性质的 2 或 4。

当然,我不是天生就有这种能力的,我是通过大量的例子来学习的。
相比之下,我们认为计算机执行的任务要求他们使用一组预先知道的有限规则来处理数据。这似乎没有提供他们需要学习的灵活性,根据经验改变他们的行为,以努力提高他们未来的表现。
然而,机器学习提供了允许程序从其经验中学习的技术。本专栏介绍了神经网络,一种旨在模拟生物神经组织的编程范例,以及允许它们学习提高性能的数学理论。
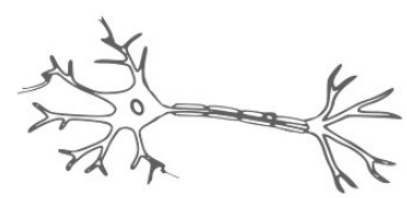
浅谈神经组织
这里显示的是神经元的示意图,一种特殊的细胞,如人类神经系统中的细胞。用非常简单的术语来说,神经元利用电化学过程来评估输入信息和作出决定。
神经元通过树突接收信息,我们可以把左侧的细长触角看作输入通道。在静息状态下,神经元在神经元内保持离子浓度,在细胞膜上产生 - 70 mV 的电位。通过树突接收到的信号可以通过改变神经元内这些离子的浓度来影响这种电位。如果电位增加到某个阈值以上,神经元就会被激活,并通过将电位提高到 40 mV 来响应。这创造了一个强大的电信号,被称为动作电位,它沿着轴突传输,它显示在右上方,作为输出通道。
神经元通过突触系统连接在一起,其中一个神经元的轴突 (输出) 连接到另一个神经元的树突 (输入)。突触通过调节从一个神经元传递到另一个神经元的动作电位,表现出不同类型的行为。首先,动作电位所携带的信号强度因突触而异。第二,神经元通过一个突触接收到的信号可能导致电位增加,这使得神经元更有可能被激活。这样的突触叫做兴奋性。相反,通过另一个突触接收到的信号可能会降低电位,从而降低神经元被激活的可能性。我们称这些突触为抑制性.
概括地说,我们将提醒注意这一进程的两个重要部分。首先,每个神经元都有一个阈值,其电位在激活前必须达到。第二,每个突触以不同的力量和作用将动作电位从一个神经元传递到另一个神经元。
最值得注意的是,神经元的激活阈值和突触的传递特性都会发生变化,这样,神经组织就能够自我重组以提高其性能。这就是神经组织学习的意义。
神经组织的数学模型
我们现在将创建一个神经元的简单数学模型,这将最终形成我们的神经网络的构建块。让我们从一个简单的神经元模型开始。
假设我们想预测一名奥林匹克运动员是否会在半途而废中赢得一枚奖牌。在作出预测时,我们可能会用到很多因素,但我们会把重点放在以下三个方面来保持简单:
(1) $x_1$ 是运动员在比赛前训练的小时数,
(2) $x_2$ 运动员在比赛前一小时吃的巧克力甜甜圈的数量,
(3) $x_3$ 是运动员播放泰勒 · 斯威夫特最新专辑的次数。
这是我们神经元的模型。输入 $x_1$, $x_2$ 和 $x_3$ 通过突触传递到神经元,在那里它们被加工成输出 $y$。
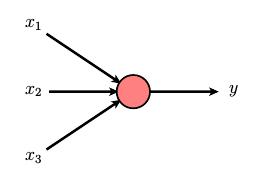
记住突触表现出不同强度的兴奋性或抑制性行为,我们指定了一个权重 \(\omega_{i}\), 对于每个突触,将输入聚合为 $$w _ { 1 } x _ { 1 } + w _ { 2 } x _ { 2 } + w _ { 3 } x _ { 3 }.$$
兴奋性突触的重量为正,而抑制性突触的重量为负值。
还请记住,当来自树突的聚集信号达到某个阈值 $\theta$ 时,神经元就会被激活。
然后我们定义
$$y = \left\{\begin{array} { l l } { 1 } & { \text { if } \sum _ { i } w _ { i } x _ { i } \geq \theta } \\ { 0 } & { \text { if } \sum _ { i } w _ { i } x _ { i } < \theta }. \end{array}\right.$$
如果我们想使用这个模型进行预测,我们需要为权重选择值 \(\omega_{i}\) 和阈值 $\theta$。
我们可以开始使用我们的直觉。如 $x_1$ 训练时间的长短,应该对运动员的表现做出显著的兴奋贡献。因此,我们可以选择 \(\omega_{1}\) 为很大的正数。在比赛前吃很多巧克力甜甜圈可能不是个好主意,所以我们希望 $x_2$ 起到强烈的抑制作用。我们可以将一个相当大的负数分配给 \(\omega_{2}\)。而仇恨者可能会选择 \(\omega_{3}\) 为了发挥类似的抑制作用,我们将选择 \(\omega_{3}\) 接近于零,这意味着听 Swift 女士的讲话可能不会对运动员的表现产生显著影响。
当然,当我们选择重量时 \(\omega_{i}\) 并以这种方式开始,我们真的只是在猜测。有什么方法可以让我们的神经元学习吗?我们知道,神经组织能够根据经验调整权重和阈值,并试图提高其性能。假设我们有一些关于运动员的数据来评估他们的表现并记录输入值 $x_1$, $x_2$ 和 $x_3$。我们能找到一种方法来使用这些数据来为权重和阈值做出最佳选择吗?这将是模拟学习过程的一种数学方法。
我们将在第一次将这些想法纳入一个更广泛的框架之后再探讨这个问题。
神经网络
粗略地说,生物神经元有三种类型:感觉神经元、加工神经元和运动神经元。感觉神经元被环境的变化所激活,运动神经元则激活肌肉或腺体。这些作为组织的输入和输出。加工神经元决定对感觉神经元传递的信息作出适当的反应,并将这种反应发送给运动神经元。
为了进一步推进我们对神经组织的数学模型,我们想象将神经元彼此连接起来,如图所示。
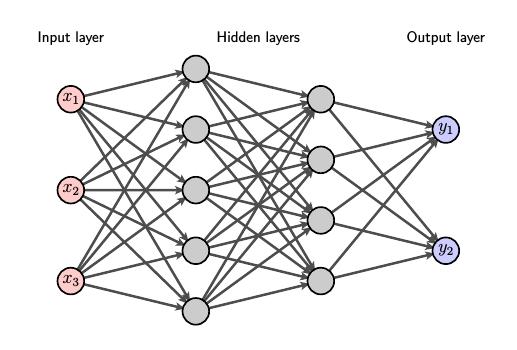
神经元排列成一层,从左侧的输入层开始。输入层中的神经元与第一隐层中的神经元相连,以此类推。我们称这种结构为神经网络.
想象一下,通过考虑如何形成一个神经网络来识别手写数字,这在实践中会是怎样的。我们的目标是将图像输入到神经网络中,如下面的图像,并输出正确的数字。

这里显示的数字来自一个称为 MNIST 数据库的公开的数字来源,该数据库最初是由国家标准和技术研究所创建的。这个数据库包含 70,000 幅图像;每个图像都是 28×28 像素数组,每个像素记录 0 到 255 之间的灰度。
这 70,000 张图像被分解成一组 60,000 张 “训练图像” 和 10,000 张测试图像。我们很快就会看到,我们使用训练图像来选择每个突触的权重和每个神经元的阈值,以优化我们的网络识别数字的准确性。然后,我们使用测试数据来确认我们的选择概括为一组新的数据。当我们将图像输入到神经网络中时,我们将输入每个像素的灰度值。这意味着 \(28^{2} = 784\) 投入,$x_0,x_1,\cdots,x_{784}$。我们的网络将有 10 个输出,$y_0,y_1,\cdots,y_9$。当我们输入一个表示数字的图像时
$$y _ {j} = \left\{ \begin{array} { l l } { 1 } & { \text { if } j = k } \\ { 0 } & { \text { if } j \neq k } \end{array} \right.$$我们现在很清楚输入和输出层是什么样子的。在它们之间添加层,即所谓的隐藏层,使我们的网络具有更强的分辨能力来识别数字。例如,假设没有隐藏层,因此输入层直接连接到输出层。这意味着每个输出,比如说 $y_0$,由我们选择的 784 个权重和一个阈值决定。如果我们有更多的参数可供选择,我们可能会提高我们的网络识别 “0” 的能力。添加隐藏层会给我们提供这些参数。现在介绍两个相对较小的改变,我们的神经元模型,其用途将很快变得清楚。首先,当满足如下条件时,神经元的输出为 1,
$$\sum _ {i} w _ { i } x _ { i } \geq \theta$$如我们所见,引入偏差 $b= − $\theta$$,并将此条件写为如下形式
$$\sum _ {i} w _ { i } x _ { i } + b \geq 0.$$其次,我们的一个神经元目前的输出要么是 0,要么是 1。如果我们定义
$$z = \sum _ {i} w _ { i } x _ { i } + b$$则输出函数 Z 是一个步长函数。
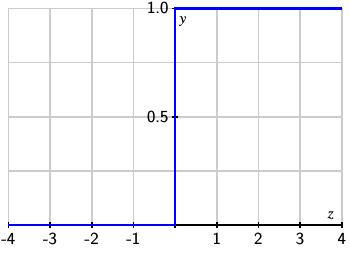
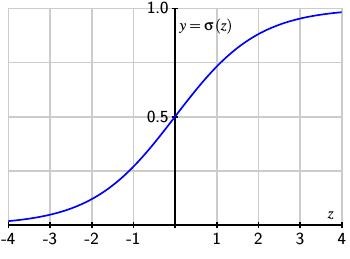
由于允许输出的连续范围在 0 到 1 之间是有用的,所以我们引入 Sigmoid 函数 $$\sigma (z) = \frac { 1 } { 1 + e ^ { - z } }.$$
如下图所示,σ(z) 是对阶梯函数的连续逼近。
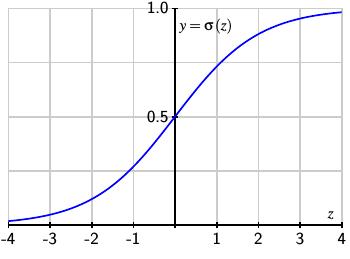
我们现在将神经元的输出定义为
$$y = \sigma \left(\sum _ { i} w _ { i } x _ { i } + b \right)$$我们的条件是用若 \(\sum_{i}^{}{w_{i}x_{i} + b \geq 0}\) 则 \(y \geq 0.5\) 替换若 \(\sum_{i}^{}{w_{i}x_{i} + b \geq 0}\) 则 \(y \geq 1\)。因此,我们可以解释输出函数 | y 作为我们对结果的信心或我们的预测正确的概率。例如,在我们试图从图像中识别手写数字时,我们可以解释 $y_7$ 作为数字为 “7” 的概率。
普遍性
在我们研究如何使用训练数据集来改善神经网络的性能之前,值得考虑这些网络的威力。例如,考虑识别手写数字的问题。输入图像的灰度值构成了 \({\mathbb R}^{784}\)。产出 \(y_{k} \in {\mathbb R}^{10}\)。我们的神经网络可以看作是一种近似辨识函数的尝试, \(i:{\mathbb R}^{784} \rightarrow {\mathbb R}^{10}\)。期望一个神经网络能够精确地逼近这样的函数是合理的吗?
我们将通过考虑具有连续函数的更简单的情况来说明。
f: r→[0,1] 只有一个输入和一个输出, 我们将展示如何创建一个具有近似性的隐藏层的神经网络, f 在封闭和有界区间上达到任何期望的精度。
我们将首先关注隐藏层中的神经元。给定输入 x,输出的 \(i^{\text{th}}\) 在隐藏层 \(z_{i}\) 中。在适当选择权重和阈值,函数 \(z_{i}(x)\) 可以近似于阶梯函数,其中梯度在 x=s 处.

让考虑权重为 \(\omega\) 的神经元,初始偏差 b=0,且 \(z(x) = \sigma\left( \text{wx} \right)\)。当我们增加权量 \(\omega\),函数 \(z(x)\) 更接近于阶梯函数。下图显示了 \(\omega = 1,\omega = 5\) 和 \(\omega = 10\) 的结果,说明近似度提高。
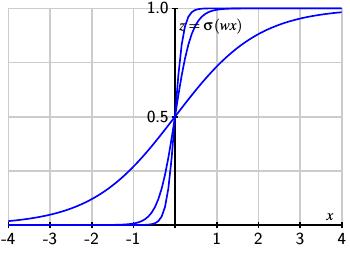
此外,我们可以通过定义 \(z\left( x \right) = \sigma(\omega(x - s))\) 来改变梯度的位置。随着我们增加 \(\omega\),我们看到了对移位阶梯函数的改进逼近。
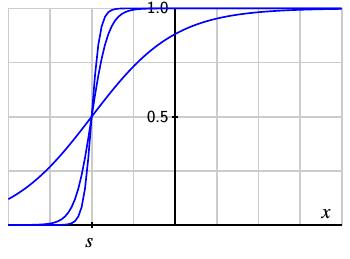
因此,对于很大的权重 \(\omega\) 和偏差 \(b = - s/w\),一个神经元的输出可以近似于一个阶梯函数。
现在让我们来看看网络的输出 $y$,这是我们想要逼近的函数 \(f(x)\),即
$$y = \sigma \left(\sum _ { i} w _ { i } z _ { i } ( x ) + b \right) \approx f ( x )$$换句话说,我们希望找到权重 \(\omega\) 和偏差 b,使得
$$\sum _ {i} w _ { i } z _ { i } ( x ) + b \approx \left( \sigma ^ { - 1 } \circ f \right) ( x ).$$如果我们定义 \(g = \sigma^{- 1} \circ f\),我们看到我们的任务是找到权重 \(\omega\) 和偏差 b,使得
$$\sum _ {i} w _ { i } z _ { i } ( x ) + b \approx g ( x ).$$假设我们的函数 \(g(x)\) 如图所示。
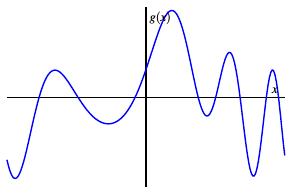
我们将对函数 \(g(x)\) 进行有限点抽样。
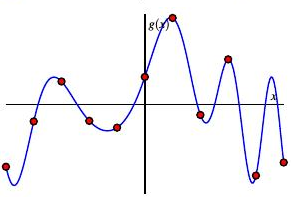
在 g 的样本点处外推 g 的阶梯函数,
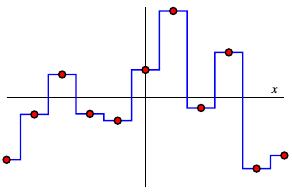
我们首先选择隐藏层中的神经元,这样函数 \(z_{i}\) 近似为一个梯级在 \(i^{\text{th}}\) 采样间隔的中点的阶梯函数。对于输出层中的单个神经元,我们选择了偏差 b 的抽样值 \(g\) 在左边端点。我们选择权重 \(\omega_{i}\),给出适当的梯度,越过间隔 \(i^{th}\) 使得
$$\begin{aligned} g ( x ) & \approx \sum _ { i } w _ { i } z _ { i } + b \\ \text { or } \quad f ( x ) & \approx \sigma \left( \sum _ { i } w _ { i } z _ { i } + b \right) \end{aligned}$$通过增加样本点的数目,我们可以用这种方法来逼近这个函数 f, 在封闭和有界区间上达到
任何期望的精度。更一般地,给定一个连续函数 \(f:{\mathbb R}^{n} \rightarrow \left\lbrack 0,1 \right\rbrack^{m}\),我们可以找到一个神经网络逼近 f 在紧子集上达到任何期望的精度。这被称为通用逼近定理,用于神经网络。
这个定理的意义通过识别手写数字的问题来说明,其中的识别函数是 \(i:{\mathbb R}^{784} \rightarrow \left\lbrack 0,1 \right\rbrack^{10}\)。逼近定理说,有神经网络将这个函数逼近到任何期望的精度。因此,我们可以开始寻找这种网络,并保证它们的存在。
我们给出的关于普适逼近定理的论点还有其他重要意义。为了改进我们的近似,我们需要在隐藏层中增加更多的采样点,从而增加更多的神经元。这说明了这样一个事实:我们可以通过在隐藏层中加入神经元来提高我们网络的力量。正如我们将要看到的那样,交换的好处是,更大的网需要更多的努力来优化。
学习过程建模
如前所述,神经组织可以通过调整突触的性质和神经元的激活阈值来重组自身,从而改善其性能。我们想在我们的神经网络中模拟这种行为。特别是,我们希望修改网络中的权重和偏差,以优化其性能。
在深入研究这个问题之前,让我们先介绍一些表示法。考虑下面的网络,它有一个输入层、一个输出层和一些隐藏层。
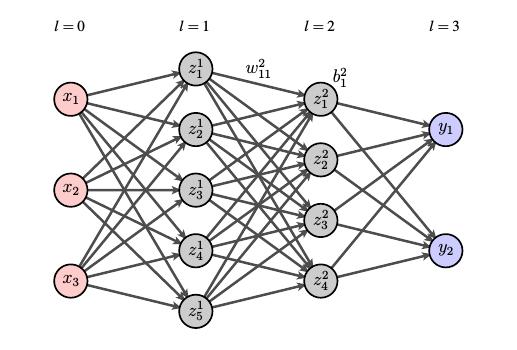
这些层将被索引 \(l\) 带着 \(l\) =0 描述输入层和 \(l\) =L 描述输出层。记住,偏差是每个神经元的属性,所以 \(b_{j}^{l}\) 将表示 \(l\) 层内神经元 \(j^{th}\)。
每个突触都有一个相应的权重,所以我们用 \(\omega_{\text{jk}}^{l}\) 连接 \(l - 1\) 层内神经元 \(k^{\text{th}}\) 和 \(l\) 层内神经元
\(j^{th}\)。然后我们有
$$z _ {j} ^ { l } = \sigma \left( \sum _ { k } w _ { j k } ^ { l } z _ { k } ^ { l - 1 } + b _ { j } ^ { l } \right).$$我们认为这个神经网络描述了一个函数 \(f:{\mathbb R}^{n} \rightarrow {\mathbb R}^{m}\),这里 n 是输入的数量 m 是产出数量。
为了使我们的目标更加具体,让我们回到从数字图像中识别手写数字的问题。辨识函数 \(i:{\mathbb R}^{784} \rightarrow {\mathbb R}^{10}\) 有这样的性质,比如 \(x = 2\),有 \(i(x) = (0,0,1,0,0,0,0,0,0,0)\)。
摆在我们面前的任务是选择权重 \(\omega_{\text{jk}}^{l}\) 和偏差 \(b_{j}^{l}\) 使得函数 \(f\) 定义的神经网络有效地逼近了辨识函数 \(i\)。记住,MNIST 手写体数字数据库包含 60,000 个 “培训” 图像 \(x_{1},x_{2},\cdots,x_{60000}\)。我们将选择权重和偏差,使神经网络和识别函数在这些训练图像上的差异尽可能小。更具体地说,最小化最小二乘函数 $E$,衡量净产出的总差额 \(f(x)\) 和识别函数 \(i(x)\):
$$E = \frac {1} { 2 } \sum _ { m } \left\| f \left( \mathbf { x } _ { m } \right) - i \left( \mathbf { x } _ { m } \right) \right\| ^ { 2 }$$在所有训练图像上取和。函数 $E$ 是权值和偏差的函数,所以
$$E = E \left(w _ { j k} ^ { l } , b _ { j } ^ { l } \right),$$我们想要找到 \(\omega_{\text{jk}}^{l}\) 和 \(b_{j}^{l}\) 来最小化 $E$.
这很像是微积分中的经典优化问题,所以我们的第一个想法是通过解方程找到 $E$
$$E = E \left(w _ { j k} ^ { l } , b _ { j } ^ { l } \right),$$不幸的是,考虑到较大的权重和偏差,发现这是不可行的。
相反,我们选择了一种迭代方法,称为梯度下降。将权重表示为 \(W = \omega_{\text{jk}}^{l}\) 和偏差 \(B = b_{j}^{l}\),我们首先为初始权重和偏差选择随机值 \((W_{0},B_{0})\)。最有可能的是,我们的选择不会减少 $E$,但是,正如我们稍后描述的,我们可以计算梯度∇E\((W_{0},B_{0})\),这就告诉我们要往哪个方向移动以减少 $E$。我们在与梯度相反的方向上迈出了一小步,通过定义
$$\left( W _ { 1 } , B _ { 1 } \right) = \left( W _ { 0 } , B _ { 0 } \right) - \epsilon \nabla E \left( W _ { 0 } , B _ { 0 } \right)$$也就是说,我们的下一组权量和偏差 \((W_{1},B_{1})\) 是从我们随机选择的权量和偏差中得到的。
\((W_{0},B_{0})\) 通过向 \(-\nabla E(W_{0},B_{0})\) 的方向移动。这样可以减小误差,使我们的新神经网络在训练数据上更好地逼近辨识函数 \(i\)。换句话说,神经网络提高了训练数据的性能。它学到了!当然,我们可以重复这个过程:
$$\begin{array} { l } { \left( W _ { 2 } , B _ { 2 } \right) = \left( W _ { 1 } , B _ { 1 } \right) - \epsilon \nabla E \left( W _ { 1 } , B _ { 1 } \right) }, \\ { \left( W _ { 3 } , B _ { 3 } \right) = \left( W _ { 2 } , B _ { 2 } \right) - \epsilon \nabla E \left( W _ { 2 } , B _ { 2 } \right) }, \end{array}$$在每一步,我们可以期待网络的性能得到改善。参数 \(\varepsilon\) 称为 “学习速率”,其值为 \(\varepsilon\),我们取大值梯度,可能会越过最低值。当 \(\varepsilon\) 很小,我们取小值梯度,可能需要许多步骤才能接近 $E$。显然,有些想法需要选择 \(\varepsilon\)。
反向传播
我们的梯度下降算法的轮廓现在是清楚的。剩下的就是设计一种计算梯度∇E 的方法。请记住,可能有数千甚至数百万的权重和偏差,用一百万个变量计算函数的梯度似乎是一项艰巨的任务。幸运的是,有一个非常有效的计算∇E 的算法,被称为反向传播,我们将在这里描述。碰巧,这也是最近自动分化专栏的主题。
我们将用一个简单的网络来解释反向传播算法,其中每个层只有一个神经元。这说明了反向传播的基本思想,同时简化了表示法。
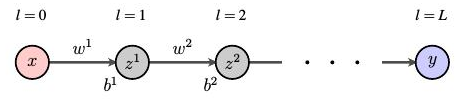
在这种情况下,我们需要计算 \(\frac{\partial E}{\partial\omega^{l}}\) 和 \(\frac{\partial E}{\partial b^{l}}\)。在我们的记法中 \(f(x) = y(x)\),由于 \(E = \frac{1}{2}\sum_{m}^{}{(f(x_{m})} - i(x_{m}))^{2}\),我们有
$$\frac { \partial E } { \partial w ^ { l } } = \sum _ { m } \frac { \partial } { \partial w ^ { l } } \left[ y \left( x _ { m } \right) \right] \left( y \left( x _ { m } \right) - i \left( x _ { m } \right) \right)$$我们在计算时找到一个类似的表达式 \(\frac{\partial E}{\partial b^{l}}\),这意味着为了找到梯度∇E 我们只需要计算
$$\frac { \partial y } { \partial w ^ { l } } \text { and } \frac { \partial y } { \partial b ^ { 2 } }$$在 “向前” 通过神经网络时,我们从数据 \(x\) 开始然后从左向右移动,对每个 \(l\) 计算
$$z ^ { l } = \sigma \left( w ^ { l } z ^ { l - 1 } + b ^ { l } \right)$$这个表达式也适用于 \(y = z^{L}\) 和 \(x = z^{0}\)。请注意,链规则意味着
$$\begin{aligned} \frac { \partial z ^ { l } } { \partial z ^ { l - 1 } } & = \sigma ^ { \prime } \left( w ^ { l } z ^ { l - 1 } + b ^ { l } \right) w ^ { l } \\ \frac { \partial z ^ { l } } { \partial w ^ { l } } & = \sigma ^ { \prime } \left( w ^ { l } z ^ { l - 1 } + b ^ { l } \right) z ^ { l - 1 } \\ \frac { \partial z ^ { l } } { \partial b ^ { l } } & = \sigma ^ { \prime } \left( w ^ { l } z ^ { l - 1 } + b ^ { l } \right) \end{aligned}$$我们从左到右再来一次。我们首先注意到
$$\frac { \partial y } { \partial z ^ { L } } = \frac { \partial z ^ { L } } { \partial z ^ { L } } = 1$$我们使用链式规则向后穿过各层:
$$\frac { \partial y } { \partial z ^ { l - 1 } } = \frac { \partial y } { \partial z ^ { l } } \frac { \partial z ^ { l } } { \partial z ^ { l - 1 } } = \frac { \partial y } { \partial z ^ { l } } \sigma ^ { \prime } \left( w ^ { l } z ^ { l - 1 } + b ^ { l } \right) w ^ { l }$$然后我们有
$$\begin{aligned} \frac { \partial y } { \partial w ^ { l } } & = \frac { \partial y } { \partial z ^ { l } } \frac { \partial z ^ { l } } { \partial w ^ { l } } = \frac { \partial y } { \partial z ^ { l } } \sigma ^ { \prime } \left( w ^ { l } z ^ { l - 1 } + b ^ { l } \right) z ^ { l - 1 } \\ \frac { \partial y } { \partial b ^ { l } } & = \frac { \partial y } { \partial z ^ { l } } \frac { \partial z ^ { l } } { \partial b ^ { l } } = \frac { \partial y } { \partial z ^ { l } } \sigma ^ { \prime } \left( w ^ { l } z ^ { l - 1 } + b ^ { l } \right) \end{aligned}$$这就是反向传播算法的本质。当然,我们的解释被简化为每一层只有一个神经元,但同样的想法更普遍地适用,尽管表示法变得更加难以使用。
这是一个了不起的算法。可以证明,用这种方法计算梯度所需的计算工作量不超过计算函数的工作量的四倍。这种效率使我们能够与强大的神经网络一起工作,这些神经网络在隐藏层中有许多神经元。
其他考虑
我们现在已经看到了神经网络如何通过使用一组训练数据来寻找权重和偏差,从而最小化训练数据上的错误函数来学习。然而,还有许多其他问题我们还没有谈到。
由于迭代梯度下降算法很可能永远找不到误差的精确最小值,因此我们需要为梯度下降建立一个停止条件。记住,我们之前说过,MNIST 数据库包含一组我们称之为训练数据的 60,000 张图像和另一组我们称之为测试数据的 10,000 张图像。在梯度下降算法的每一步后,我们对神经网络应用于测试数据的误差进行了评估。我们应该期望,在提高网络在训练数据上的性能的同时,这种改进也应该推广到测试数据中。
通常发生的情况是,训练集上的错误减少到零,但是测试数据上的错误稳定在一些正值,如下所示。
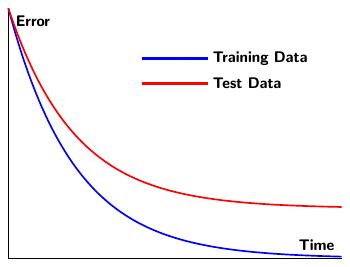
当我们继续细化权重和偏差时,我们继续从训练数据中抽取误差,而没有看到测试数据的任何改进。这是因为培训数据几乎肯定包含没有出现在测试数据中的噪声。在这种情况下,继续提高训练数据的性能只是将噪声输入到网络中,这叫做过度拟合。避免这种情况的一个简单方法是,当我们不再看到网络在测试数据上的性能有所提高时,停止梯度下降算法。然而,有更复杂的方法来解决这个问题。
对误差函数的选择可以提高梯度下降算法的效率。正如我们在上面看到的,误差函数的导数用乙状结肠函数的导数来表示 \(\sigma^{'}(z)\)。由于 \(\sigma(x) = \frac{1}{(1 + e^{- x})}\),因此 \(\sigma^{'}(z) = \sigma(1 - \sigma)\)。再看 \(\sigma\) 说明了问题的原因。
记住,权量最初是随机选择的。这意味着我们可能意外地选择了权重,使之远离它们应该达到的最佳位置。特别是,一个神经元可能会被困在一些接近的东西上,比如说,$\sigma=0$ 当它应该最优地评估到$\sigma=1$。给定 \(\sigma^{'}\),导数会很小,而梯度下降算法需要很长时间才能适当地改变权值。因此,可以有利地使用错误函数的不同选择。
总结
神经网络形成了一个丰富的学科,我们只是涉足其中。然而,在这篇简短的介绍中,我们可以看到,神经网络为计算机分类提供了一个强有力的工具。
当我们研究普适逼近定理时,我们看到,我们可以通过在隐藏层中增加更多的神经元来增加我们网络的功率。与许多隐藏层中的大量神经元一起工作称为深度学习。巨大的蚊帐提供了新的机会,也带来了新的挑战;应对这些挑战是当前大量工作的主题。
神经网络正在应用于越来越广泛的问题。正如我们在本文中所看到的,设计识别手写字符的网是可能的。事实上,使用 74 行 Python 代码构建一个由 30 个神经元组成的网络相当容易,这些代码可以正确识别 MNIST 测试数据集中 95% 的图像 (参见参考文献中引用的 Nielson 的书)。更普遍的是,神经网络应用于图像检测、医学诊断和股票市场预测。
当然,一个网络只和我们用来训练它的数据一样好。任何出现在培训数据中的偏见都将被内置到网络中,并影响到网络做出的任何决定。
同样令人不安的是,很难知道一个经过训练的神经网络究竟是如何工作的。梯度下降算法在不需要人工干预的情况下,发现了几乎最优的权重和偏差。这意味着我们失去了描述网络中任何特定神经元的作用的能力。在某种意义上,我们相信网络会做出决定,而不知道这些决定是如何做出的。随着神经网络在我们的社会中变得越来越普遍,这肯定会引起伦理上的关注。
| 作者简介: | David Austin,Grand Valley State University |
| 译者简介: | 杨艳秋,吉林师范大学数学学院副教授 |
| 杨宇,吉林师范大学,统计学专业三年级 | |
| 原文链接: | http://www.ams.org/publicoutreach/feature-column/fc-2018-03 |




