椭圆函数正篇:Gauss与AGM(6-2)

[题图来自 Gauss1805 年的笔记Scheda An(见 Gauss 全集第十卷第二册,102 页-103 页),笔记的题名为Cereri, Palladi, Junoni sacrum。根据 Gauss 日记的记载 [Gauss 日记 122 条],Gauss 在 1802 年-1804 年一直忙于天文观测及其相关计算,直到 1805 年 Gauss 才返回到纯粹数学的研究上来。这一张图来自Scheda An的第 7 页。在Scheda An的第 8 页上有 Gauss 写下的模形式 $p (\tau)$ 满足的若干函数方程。根据这些记载以及 Gauss 日记的记录,Gauss 全集第十卷的编辑 Schlesinger 断定,Gauss 在 1800 年左右就知道下面提及的模形式 $p,q,r$ 的函数方程,而 Gauss 直到 1805 年左右才开始着手研究与 $p,q,r$ 相关的同余子群的基本区域,Scheda An上的这张图正是这些基本区域的示意图。这一非常重要的概念从未落到 Abel 和 Jacobi 的手中,直到 Riemann 把它 "发展为自己理论中受到钟爱的工具"(见 Klein《数学在 19 世纪的发展》第一卷,齐民友译,38 页)。Gauss 的基本区域与我们通用的记法不同之处在于,他的基本区域是我们通用的基本区域顺时针旋转 90 度以后得到的图形。在下文中我们一概采用现代记法而不采用 Gauss 的记法。]
前情提要:Gauss 所发现的函数
$$\begin {align} p (\tau)&=\sum_{n\in\mathbb {Z}} e^{\pi+in^2\tau}\\q (\tau)&=\sum_{n\in\mathbb {Z}}(-1)^ne^{\pi+in^2\tau}\\r (\tau)&=\sum_{n\in\mathbb {Z}} e^{\pi+i (n+1/2)^2\tau}\end {align}\\$$
都是上半复平面 $\Im {\tau}>0$ 上的解析函数,而且它们都满足某些对称性,这些对称性可以由函数方程刻画,例如
$$p^2 (\frac {\tau}{2\tau+1})=(2\tau+1) p^2 (\tau)$$
那么我们应当如何刻画 $p,q,r$ 的所有可能的对称性 [换言之,这些函数在何种变换群下保持不变]?这些对称性与复数 AGM 的迭代过程有什么关系?这是我们本篇集中探讨的内容。
1861 年 Gauss 的学生兼密友Johann Franz Encke曾经提及过他与 Gauss 的几次私人谈话,在谈话中 Gauss 强调,数学乃是“视觉的科学”(eine Wissenschaft für das Auge)[原文见 Kronecker 全集第五卷,391 页]。遵循 Gauss 这个观点,我们就必须引入复平面这个几何工具,它对于我们理解 $p,q,r$ 及其背后的模形式大家族有着至关重要的作用。
Ex.函数 $p^2 (\tau)$ 满足以下函数方程:
$$p^2 (\tau+2)=p^2 (\tau)$$ $$p^2 (\frac {\tau}{2\tau+1})=(2\tau+1) p^2 (\tau)$$
它们刻画的正是 $p^2 (\tau)$ 在线性分式变换$\tau\mapsto\tau+2$ 以及 $\tau\mapsto\frac {\tau}{2\tau+1}$ 作用下所满足的"对称性"。我们对这些变换进行复合,就可以导出更多的函数方程。那么这些函数方程的具体形式是什么?
我们知道,线性分式变换中的"线性"二字来自于以下事实:两个线性分式变换的复合等价于两个 $2\times2$ 非奇异矩阵的复合。因此,线性分式变换 $\tau\mapsto\tau+2$ 与 $\tau\mapsto\frac {\tau}{2\tau+1}$[及其逆] 的所有复合等价于 $\begin {pmatrix} 1&2\\0&1\end {pmatrix}$ 与 $\begin {pmatrix} 1&0\\2&1\end {pmatrix}$ 生成的群。这意味着,这些线性变换的复合都是下面的线性分式变换群的元素 [这就是著名的 modular group $\Gamma (1)$]:
$$\tau\mapsto\frac {a\tau+b}{c\tau+d},a,b,c,d\in\mathbb {Z},ad-bc=1$$
进一步观察我们可以看出,除了要求 $ad-bc=1$ 以外,我们其实还得要求 $b,c$ 均为偶数。所有满足 $ad-bc=1$,$b,c$ 均为偶数的整数矩阵 $\begin {pmatrix} a&b\\c&d\end {pmatrix}$ 在矩阵乘法下也构成一个群,我们称之为层次 2 的主同余子群(principal congruence subgroup of level 2,这是源自 Klein 的术语,通用记号为 $\Gamma (2)$)。
一个自然的问题是:$\begin {pmatrix} 1&2\\0&1\end {pmatrix}$ 与 $\begin {pmatrix} 1&0\\2&1\end {pmatrix}$ 生成的群与 $\Gamma (2)$ 之间的关系是什么?我们可以用代数方法 [辗转相除法] 和几何方法两种方法来解决这个问题。两种方法中几何方法涵盖了更多的信息,所以我们把代数方法放在一边,把注意力集中在这个问题的几何方法上。
线性分式变换群
$$\tau\mapsto\frac {a\tau+b}{c\tau+d},a,b,c,d\in\mathbb {Z},ad-bc=1\\$$
最自然的作用对象是上半平面 $\Im\tau>0$。上半平面的任意一点在这个群的作用下都有无穷多个像点,如下图所示:
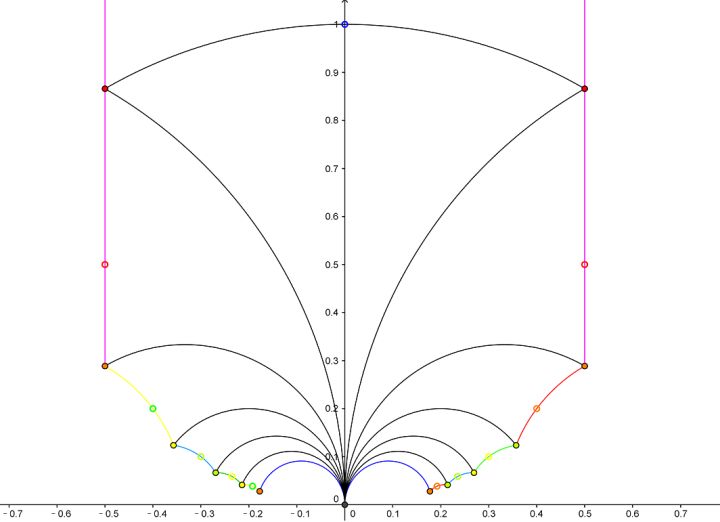 离散线性分式变换群在上半平面的作用[TSUBASA!]
离散线性分式变换群在上半平面的作用[TSUBASA!]
空心圈点是上半平面的点 $i$ 在这个群作用下的像。直观看来,这些像点是越来越接近实轴的。换言之,在群的作用下,上半平面上的点 $\tau$ 的虚部趋于 0。这一点很容易用代数计算来证实。通过计算我们可以得到 $\Im\frac {a\tau+b}{c\tau+d}=\frac {(ad-bc)\Im\tau}{\vert+c\tau+d\vert^2}=\frac {\Im\tau}{\vert+c\tau+d\vert^2}$。$c,d$ 是离散的整数,当 $c,d$ 中的一者趋于无穷,那么 $\Im\frac {a\tau+b}{c\tau+d}$ 的值必然趋于 0。这一观察还带来一个结论,那就是对于给定的 $\tau$,$\Im\frac {a\tau+b}{c\tau+d}$ 存在最大值。
上面的推理一样适用于 $\begin {pmatrix} 1&2\\0&1\end {pmatrix}$ 与 $\begin {pmatrix} 1&0\\2&1\end {pmatrix}$ 生成的群与 $\Gamma (2)$。我们记前者为 $G$,那么上半平面上总存在点 $\tau$, 它的虚部不小于它在 $G$ 作用下的所有像点的虚部。据此我们可以得知,
$\frac {\Im\tau}{\vert+\pm2\tau+1\vert^2}\leq\Im\tau$, 也就是 $\vert\pm2\tau+1\vert^2\geq1$。由于 $\begin {pmatrix} 1&2\\0&1\end {pmatrix}$ 作用并不改变 $\tau$ 的虚部,因此我们可以把 $\tau$ 的实部限制在 $-1$ 到 $1$ 之间 [为什么?]。因此,我们就得到了以下的上半平面的区域 $D:\Im\tau>0,\vert\pm2\tau+1\vert\geq1,-1\leq\Re\tau\leq1$ 的图像:
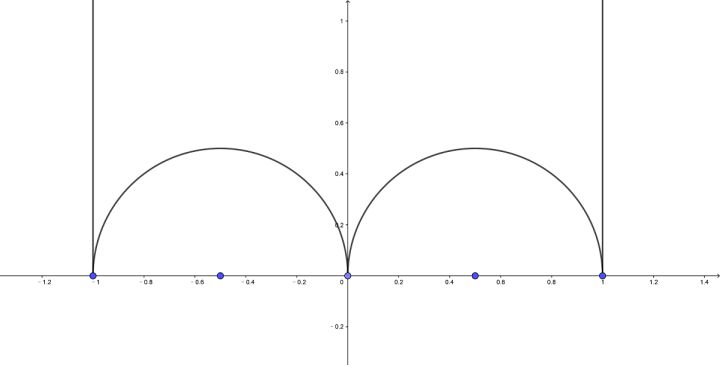 Gamma(2) 的基本区域 $D$ (与模形式 $p$ 关联)
Gamma(2) 的基本区域 $D$ (与模形式 $p$ 关联)
[注:Gauss 在 1827 年的笔记中 (见 Gauss 全集第三卷,477-478 页) 明确地给出了这个基本区域的图形,然而 Gauss 全集的第一任编辑 Schering 完全没理解 Gauss 的意思,把这个图画错了。直到 1898 年 Klein 负责主持 Gauss 全集的编辑工作以后,这个错误才由 Robert Fricke 更正过来 (见 Gauss 全集第八卷,105 页)。]
我们可以根据这一观察来导出 $\Gamma (2)$ 与群 $G$ 之间的关系。根据上面的推理,我们如果取区域中 $D$ 的点 $\tau$, 并任意取 $\gamma\in\Gamma (2)$,那么我们总能在 $G$ 中找到元素 $g$,使得 $g\gamma\tau$ 也属于这一区域。我们取 $D$ 中的点 $i$, 并且记 $g\gamma=\begin {pmatrix} u&v\\x&y\end {pmatrix}$,我们就会得到限制
$$\vert vy+ux\vert\leq u^2+v^2$$ $$\vert vy+ux\vert\leq x^2+y^2$$ $$uy-vx=1,u,v,x,y\in\mathbb {Z},v,x\,\text{are even numbers}$$这些约束条件给出的唯一可能就是 $g\gamma=\pm I$,$I$ 是单位矩阵 [为什么?],因此我们已经导出,线性分式变换 $\tau\mapsto\tau+2$ 与 $\tau\mapsto\frac {\tau}{2\tau+1}$ 是线性分式变换群 $\tau\mapsto\frac {a\tau+b}{c\tau+d},\begin {pmatrix} a&b\\c&d\end {pmatrix}\in\Gamma (2)\\$
的生成元。
上面的推理奠定了我们本篇内容的基石。这一推理可以产生以下的推论:
任意给定上半平面 $\Im\tau>0$ 中的一点 $\tau$, 我们总可以找到 $\gamma\in\Gamma (2)$,使得 $\gamma\tau$ 落在我们指定的区域 $D$ 内。这一区域 $D$ 我们称之为 $\Gamma (2)$ 的基本区域 (Fundamental Domain, Fundamentalbereich);
$\begin {pmatrix} 1&2\\0&1\end {pmatrix}$ 与 $\begin {pmatrix} 1&0\\2&1\end {pmatrix}$ 生成的群并不是 $\Gamma (2)$,而是它的一个指数为 2 的子群,这个子群同构于 $\Gamma (2)/\{\pm I\}$, 或者可以说,它的元素是 $\Gamma (2)$ 中满足 $a\equiv d\equiv1\pmod 4$ 的矩阵 $\begin {pmatrix} a&b\\c&d\end {pmatrix}$。我们记这个群为 $\Gamma (2)_0$。通过归纳法可以证明,给定 $\begin {pmatrix} a&b\\c&d\end {pmatrix}\in\Gamma (2)_0$,我们有 $p^2 (\frac {a\tau+b}{c\tau+d})=(c\tau+d) p^2 (\tau)\\$ 这是我们在这一系列中真正展示的第一个模形式。
注意到 $p^2 (\tau+1)=q^2 (\tau)$, 借此我们可以得到 [为什么?]:给定 $\begin {pmatrix} a&b\\c&d\end {pmatrix}\in\Gamma (2)_0$,有 $q^2 (\frac {a\tau+b}{c\tau+d})=(-1)^{c/2}(c\tau+d) q^2 (\tau)\\$ 这是所谓的带有乘子 (multiplier) 的模形式。从这里我们可以看出,如果 $\begin {pmatrix} a&b\\c&d\end {pmatrix}\in\Gamma (2)_0$ 且 $c\equiv0\pmod4$, 那么我们有 $q^2 (\frac {a\tau+b}{c\tau+d})=(c\tau+d) q^2 (\tau)$。所有这样的矩阵依然构成一个群,我们称之为 $\Gamma_2 (4)$。这个群的基本区域完全可以用与 $\Gamma (2)$ 一致的方法导出。具体可以写为 $D^\prime:\Im\tau>0,\vert\pm4\tau+1\vert\geq1,\vert\pm4\tau+3\vert\geq1,-1\leq\Re\tau\leq1$。
[请读者思考:$r^2 (\tau)$ 在 $\Gamma (2)$ 作用下满足什么样的函数方程?$p,q,r$ 在我们提到的各种群 (尤其是 modular group$\Gamma (1)$) 的作用下又是如何变化的?(Gauss 当然知道这些问题的答案 [参见 Gauss 全集第十卷第一册,224 页])]
我们不清楚 Gauss 的推理过程是否与我们的推理重合。尽管我们不知道 Gauss 具体的推理过程,但已有的材料倾向于表明:Gauss 知道上面我们写下的所有结论,绝大多数思想成型的时间不会晚于 1827 年,最基本的思想更是早在 1800 年或 1805 年就已经成型,可惜的是他始终没有把自己的思想写成文章,我们所看到的只是思想的断片而已。
经过漫长的铺垫以后,我们才能尝试去解决 Gauss 的问题:
问题:给定迭代的初值 $a_0=a,b_0=b,a,b\in+\mathbb {C}$[我们舍去 $ab=0$ 或 $a^2=b^2$ 的平凡情形]。迭代过程由 $\begin {cases} a_{n+1}=(a_n+b_n)/2\\b_{n+1}=\sqrt {a_nb_n}\end {cases}$ 确定。由于复数域上的分数次幂是多值函数,因此一般每次迭代会产生两个不同的 $b_{n+1}$ 的值。我们想要知道,这一迭代过程所有可能的极限值是什么。
我们仍然可以从上一篇的 toy model 的分析过程中获取灵感。上一篇中对于 toy model 中的绝大多数分析都可以直接用到 Gauss 的问题上去。
我们仍然规定 "好的" 复数对 $(a_n,b_n)$ 满足$|a_n-b_n|\leq|a_n+b_n|$。如果定义 $M_n=\max (|a_n|,|b_n|)$,那么 $M_n$ 依然是单调递减的,从而存在极限;
如果 $(a_n,b_n)$ 是 "不好" 的,那么我们有 $M_{n+2}\leq+cM_n$ 对某个严格小于 1 的正实数 $c$ 成立。因此如果迭代中有无限多对 $(a_n,b_n)$ 是 "不好" 的,那么迭代的极限必然是 0。[其实我们可以定 $c=0.86$,请读者推理一下,这个值是怎么来的?];
序列中只有有限多对 "不好" 的 $(a_n,b_n)$ 的情形是我们需要重点考察的对象。Gauss 早在 1810 年左右就计算过这样的序列 [见 Gauss 全集第十卷第一册,219 页],他的计算显示,取初值 $a_0=3,b_0=1$,如果只有第一次迭代是 "不好" 的 ($a_1=2,b_1=-\sqrt {3}$),那么迭代数值上收敛到 $0.2469962+0.6318686i$。类似于我们上篇的推理,我们可以证明,如果序列中只有有限多对 "不好" 的 $(a_n,b_n)$,那么 $\{a_n\},\{b_n\}$ 收敛到同一个值。我们把这个证明交给读者来完成;
-
我们在上篇中用函数 $p,q$ 来表示序列 $\{a_n\},\{b_n\}$:
$$a_n=\lambda_n+p^2 (\tau_n)$$ $$b_n=\lambda_n+q^2 (\tau_n)$$此时我们就要求,对于某正整数 $N$,对 $n\geq+N$ 总有 $\Re {\frac {q^2 (\tau_n)}{p^2 (\tau_n)}}\geq+0$. 这一不等式所确定的 $\tau_n$ 属于上半平面的哪些区域呢?细心的读者或许已经看出来,我们在上篇中已经处理过关于简化模型的类似问题。我们这里的问题当然远比简化情形中的三角函数要困难得多;
-
依 Jacobi 和 Legendre 等人的传统记法,令 $k^\prime (\tau)=\frac {q^2 (\tau)}{p^2 (\tau)},k (\tau)=\frac {r^2 (\tau)}{p^2 (\tau)}$,必有 $(k^\prime (\tau))^2+(k (\tau))^2=1$[为什么?]。根据前面关于 $p,q$ 函数方程的讨论,我们知道
$$k^\prime\left (\frac {a\tau+b}{c\tau+d}\right)=(-1)^{c/2} k^\prime (\tau),\begin {pmatrix} a&b\\c&d\end {pmatrix}\in\Gamma (2)$$
所以我们考虑 $k^\prime (\tau)$ 在 $\Gamma_2 (4)$ 的基本区域 $D^\prime$ 上的取值就可以了;
下图中我们把两个基本区域 $D,D^\prime$ 放在同一张图里。
根据 $k^\prime (\tau)$ 的定义,我们知道这个函数在虚轴上总是取非负实数值。如果我们用一下Gauss 与 AGM (V-2)提到的Jacobi 乘积,我们还能进一步断定,如果 $\tau$ 沿着虚轴从 $i\infty$ 移动到 $0$,$k^\prime (\tau)$ 的值从 1 单调递减到 0 [为什么?]。我们又知道 $k^{\prime}(\tau+1)=\frac {1}{k^{\prime}(\tau)}$ 以及 $k^{\prime}\left (\frac {\tau}{\tau+1}\right)=-i\frac {k^{\prime}(\tau)}{k (\tau)}$。因此我们可以断定:1)当 $\tau$ 沿着弧 CE 从 C 移动到 E,那么 $ik^\prime (\tau)$ 单调从 $0$ 变到正无穷;2)当 $\tau$ 沿着射线 $\Re\tau=1,\Im\tau>0$ 从 E 移动到无穷远处,那么 $k^\prime (\tau)$ 单调从正无穷降到 1。根据这两个观察以及幅角原理,我们就可以确定如下事实 [区域 D 的边界要稍加注意。边界上两点如果在 $\Gamma_2 (4)$ 作用下等价,那我们把它们算作同一点],这一事实是Picard 小定理的某个证明的关键要素:$k^\prime (\tau)$ 将 $\Gamma (2)$的基本区域 $D$ 一对一地映射到去掉两点的右半平面 $\Re\tau\geq0,\tau\neq+0,1$。[注:Gauss 本质上知道我们这里关于 $k^\prime (\tau)$ 的一切结论 [见 Gauss 全集第三卷 477-478 页],只是写法稍有不同。Gauss 在手稿中是这样描绘 $\Gamma (2)$ 的基本区域的:$D:\Im\tau>0,-1\leq\Re\tau\leq1,-1\leq\Re (-1/\tau)\leq1$。Schering 就是在整理 Gauss 这部分遗稿时出了错。Gauss 还给出了 $\Gamma_2 (4)$ 的基本区域的一个子域 $D^{\prime\prime}$, 这一区域在 $k^\prime (\tau)$ 映射下的像是去掉三个点的单位圆盘。有兴趣的读者可以尝试绘制一下 $D^{\prime\prime}$ 的形状。]
-
我们只有武装到这个地步才能解决 Gauss 的问题。设序列 $\{a_n\},\{b_n\}$ 的初值为 $a_0=\lambda_0p^2 (\tau_0),b_0=\lambda_0q^2 (\tau_0)$,$\tau_0$ 位于 $\Gamma_2 (4)$ 的基本区域 $D^\prime$ 中。我们在上篇中已经提过,每一次迭代等价于
$$\lambda_{n+1}=\frac {\lambda_n}{4\tau_ns_n+1}$$ $$\tau_{n+1}=\frac {2\tau_n}{4\tau_ns_n+1}$$
$s_n$ 的值取 0 或 1。如果 $\{s_n\}$ 的所有值都取 0,那么序列 $\{a_n\},\{b_n\}$ 收敛到 $\lambda_0$,而且每一对 $(a_n,b_n),n\geq1$ 都是 "好的"。Gauss 称这个值 $\lambda_0$ 为初值 $a_0,b_0$ 的最简 [算术几何] 平均值(einfachst Mittel)。
-
上面的递推式直接的推论是
$$\lambda_{n}=\frac {\lambda_0}{4K_n\tau_0+1}$$ $$\tau_{n}=\frac {2^n\tau_0}{4K_n\tau_0+1}\text{ 其中 } K_n=\sum_{i=0}^{n-1} 2^is_i.$$
假设从某个标号 $N$ 起 $\Re\frac {b_n}{a_n}\geq+0,n\geq+N$。那么我们总能找到某个矩阵 $\begin {pmatrix} a&b\\c&d\end {pmatrix}\in\Gamma_2 (4)$,使得 $\bar {\tau}_N=\frac {a\tau_N+b}{c\tau_N+d}$ 位于 $\Gamma (2)$ 的基本区域当中 [为什么?]。我们记 $a_N=\bar {\lambda}_Np^2 (\bar {\tau}_N),b_N=\bar {\lambda}_Nq^2 (\bar {\tau}_N)$, 那么根据我们前面关于最简算术几何平均值的推理,序列 $\{a_n\},\{b_n\}$ 收敛到 $\bar {\lambda}_N$[为什么?]。
$\bar {\lambda}_N$ 和 $\lambda_0,\tau_0$ 的关系是什么?根据 $p^2 (\tau),q^2 (\tau)$ 在 $\Gamma_2 (4)$ 的变换下满足的规律,我们可以写出 $\begin {align}\bar {\lambda}_N&=\frac {\lambda_N}{c\tau_N+d}=\frac {\lambda_0}{(4dK_N+2^Nc)\tau_0+d}\end {align}\\$ 换言之,迭代中生成的所有非平凡的平均值都可以表示为 $\frac {\lambda_0}{\bar {c}\tau_0+\bar {d}}$, 其中 $\bar {c}=4dK_N+2^Nc,\bar {d}=d$。两者是互质的整数而且 $\bar {c}\equiv0\pmod4,\bar {d}\equiv1\pmod4$。
反过来我们要问,是不是所有形如 $\frac {\lambda_0}{\bar {c}\tau_0+\bar {d}},\bar {c}\equiv0\pmod4,\bar {d}\equiv1\pmod4,(c,d)=1$ 的复数都是迭代的极限值?答案是肯定的。我们在此给出一个序列 $\{s_n\}$ 的构造,这个构造可以保证迭代收敛到给定的 $\frac {\lambda_0}{\bar {c}\tau_0+\bar {d}}$:
构造的关键在于找到合适的矩阵 $\begin {pmatrix}\tilde {a}_n&\tilde {b}_n\\\tilde {c}_n&\bar {d}\end {pmatrix}\in\Gamma_2 (4)$, 使得 $\tau_n$ 在对应的分式线性变换作用下虚部总是足够大的。此时我们可以把 $a_n$ 重写为 $a_n=\frac {\lambda_0}{C_n\tau_0+\bar {d}} p^2\left (\frac {A_n\tau_0+B_n}{C_n\tau_0+\bar {d}}\right)\\$ 其中 $A_n=\tilde {a}_n2^n+4\tilde {b}_nK_n,C_n=\tilde {c}_n2^n+4\bar {d} K_n$。如果我们能够选取合适的 $\tilde {c}_n,K_n$,使得 $C_n$ 恒等于 $\bar {c}$,那么我们的任务就基本完成了,因为此时的 $\Im\left (\frac {A_n\tau_0+B_n}{C_n\tau_0+\bar {d}}\right)=\frac {A_n\bar {d}-B_nC_n}{|\bar {c}\tau_0+\bar {d}|^2}\Im {\tau_0}=\frac {2^n}{|\bar {c}\tau_0+\bar {d}|^2}\Im {\tau_0}$[为什么?] 此时序列的极限必然是 $\frac {\lambda_0}{\bar {c}\tau_0+\bar {d}}$。注意到 $\tilde {c}_n2^n+4\bar {d} K_n$ 恒等于 $\bar {c}$,所以我们可以给出递推关系 $\tilde {c}_0=\bar {c},2\tilde {c}_{n+1}=\tilde {c}_n-4\bar {d} s_n$。由于 $\bar {d}$ 是奇数,$\{\tilde {c}_n\}$ 各项都是 4 的倍数,我们很容易借此确定 $\{s_n\}$ 各项的值:它与 $\tilde {c}_n/4$ 的奇偶性是一致的。这样我们就完成了必要的构造。
我们重新叙述一下我们得到的结果:我们令初值 $a_0=a,b_0=b$, 并且令 $a_0=\lambda_0p^2 (\tau_0),b_0=\lambda_0q^2 (\tau_0)$,$\tau_0$ 位于 $\Gamma_2 (4)$ 的基本区域 $D^\prime$ 当中。那么复数域上的 AGM 迭代总能收敛到一个固定的极限值,这个极限值有且只有两类可能性:1)0,绝大多数的迭代过程只能收敛到这个值;2)$\frac {\lambda_0}{c\tau_0+d},c\equiv0\pmod4,d\equiv1\pmod4,(c,d)=1$。
就 Gauss 现存的手稿来看,他最接近这个命题的记录出现在 Gauss 全集第十卷第一册 219 页 (Schlesinger 给它的断代是 1810 年)。他的命题可以这样描述:取 AGM 迭代的初值 $a_0=a,b_0=b,a>b$ 为正实数。迭代中我们直到第 N 次迭代之前都取 $a_n,b_n$ 的正实数值。第 N 次迭代我们取 $b_N$ 小于 0 的值。之后所有的迭代如果我们都取 " 好的”复数对 $(a_n,b_n)$, 那么迭代收敛到一个复数值 $(\mu)$。我们记初值为 $a,b$ 的最简平均值为 $\mu$, 初值为 $a,\sqrt {a^2-b^2}$ 的最简平均值为 $\lambda$, Gauss 断言,$(\mu)$ 必然满足如下形式:$\frac {1}{(\mu)}=\frac {1}{\mu}+\frac {4ik}{\lambda},k\in\mathbb {Z}\\$Gauss 的命题当然只是我们上面命题的一个非常特殊的情形。至于他心中是否已经有我们本篇证明的最深刻的问题的答案,我们是完全无法回答的。
从 Gauss 手稿的日期看,他总是会间断性地回到过去提出的问题,补充和完善以前提出的问题和推理。直到 1827 年 Gauss 还在不断地修订自己关于椭圆函数的工作 (例如上面给出的 $\Gamma (2)$ 的基本域就属于这一时期的记录)。然而 Gauss 知道Abel 和 Jacobi 的工作以后似乎就放弃了自己已有的计划。Gauss 因此与椭圆函数论的历史主流无缘。推动历史的工作,就压在了年轻一代人的肩上。
思考题:Gauss 的椭圆函数理论要用到两个实数之间的算术几何平均值 (见Gauss 与 AGM (V-2))。但根据我们本篇的论述,如果初值是固定的,在复数域上我们会得到无穷多个算术几何平均值。采取不同的算术几何平均值对 Gauss定义的椭圆函数$S (u),T (u),W (u)$ 是否有影响?
| 作者: | rainbow zyop |




