一副牌要洗几次?
一个月前,我与我的孩子玩一个叫“疯狂八”的纸牌游戏。在一次比赛中,玩完了整个一副牌后我们把牌堆中的牌洗了几次再玩。可是尽管洗了牌,我们仍看到同一花色有时会从牌中连续出现。牌的次序在游戏第一部分结束洗牌之后还在那里;洗牌似乎并没有尽我们希望那么强地影响牌的次序。
这使我想知道需要洗几次牌才能保证一副牌的顺序基本是随机的?出于好奇,我很快就在Aigner和Ziegler很精彩的书《Proofs from THE BOOK》中碰到针对此问题的一篇随笔,并导致我读到Aldous和Diaconis所写的一篇精彩论文,这篇论文给出了这个问题的答案。
本专栏将解释这篇论文的几个技术和结果。令人惊讶的是,这个看似平淡无奇的问题的分析居然牵扯到广泛的甚至很深刻的数学问题,其领域包括李代数、Hochschild同调、图上的随机游动,并需要配以重要的推广方式。
首先,我们假设有n张牌,为了简单起见,我们假设所有牌只用数字1到n来标记。最初,这副牌以数字大小排序,然后我们将用某个已商定好的技术洗牌。通常的洗牌称为浅滩洗牌,这将在稍后讨论。现在我们以较为简单的一类洗牌方式开始,称为顶端随机插入洗牌法。在这个洗牌中,我们把这副牌的最上面那张牌以相同的概率随机插入到n个可用位置上。

例如,当n=3,有三种可能性,其中每一个都是同样可能的。
让我们对这个洗牌定量化。这副牌的所有次序之集用$S_n$表示,通常被称为n个字母的对称群。有n的阶乘,数学表示n!个可能的排序。如果$\pi$是牌的一个特定排序,我们将用$Q(\pi)$表示洗牌一次后得到$\pi$的概率。
考虑上面n=3的例子。如上图只移动第一张牌的话,我们看到洗牌一次后的概率为:
| $\pi$ | $Q(\pi)$ |
|---|---|
| 1 2 3 | 0.333 |
| 1 3 2 | 0.000 |
| 2 1 3 | 0.333 |
| 2 3 1 | 0.333 |
| 3 1 2 | 0.000 |
| 3 2 1 | 0.000 |
这表明,六个可能的次序中有三个是同样可能的,而其它三个是不可能的。我们可以再次洗牌。在一次、二次、三次洗牌后,三张牌的所有可能次序如下所示。为方便起见,牌在这里用颜色代表,而不是编号。

$Q^k(\pi)$将表示次序$\pi$经过$k$次洗牌后出现的概率。一点点的计算显示
| $Q^1(\pi)$ | $Q^2(\pi)$ | $Q^3(\pi)$ | $Q^4(\pi)$ | $Q^5(\pi)$ | $Q^6(\pi)$ | $Q^7(\pi)$ | $Q^8(\pi)$ | $Q^9(\pi)$ | $Q^{10}(\pi)$ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 2 3 | 0.333 | 0.222 | 0.185 | 0.173 | 0.169 | 0.167 | 0.167 | 0.167 | 0.167 | 0.167 |
| 1 3 2 | 0.000 | 0.111 | 0.148 | 0.160 | 0.165 | 0.166 | 0.166 | 0.167 | 0.167 | 0.167 |
| 2 1 3 | 0.333 | 0.222 | 0.185 | 0.173 | 0.169 | 0.167 | 0.167 | 0.167 | 0.167 | 0.167 |
| 2 3 1 | 0.333 | 0.222 | 0.185 | 0.173 | 0.169 | 0.167 | 0.167 | 0.167 | 0.167 | 0.167 |
| 3 1 2 | 0.000 | 0.111 | 0.148 | 0.160 | 0.165 | 0.166 | 0.166 | 0.167 | 0.167 | 0.167 |
| 3 2 1 | 0.000 | 0.111 | 0.148 | 0.160 | 0.165 | 0.166 | 0.166 | 0.167 | 0.167 | 0.167 |
注意到当洗牌次数进行得更多后,我们看到不同次序出现的频率变得更加均匀。我们将用$U(\pi)$表示每个排序$\pi$以同样可能性出现的概率密度;即$U(\pi) = 1/n!$。上述表中的结果表明
为了使这种说法更精确,并使得洗牌的定量分析更容易,我们需要引入一个概率密度之间的距离的概念。因此,假设$Q_1$和$Q_2$是两个$S_n$上的概率密度。首先,我们定义$Q_1$和$Q_2$在$S_n$的一个子集$A$上的差异,这是它们在$A$的所有元素上的差异之和:
然后$Q_1$和$Q_2$之间的距离是它们在$S_n$的所有子集上的最大差异:
注意到这是两个密度之间距离的非常敏感的度量。首先
接下来,想象$S_n$上的均匀分布$U$和从一个特定类型的洗牌得到的一个密度$Q$。如果这种类型的洗牌留了一张牌在原来的地方,则
考虑到集之间的最大距离为1,这是一个相当大的距离。
我们不妨检查初始分布$I$,其中$I(1 2 \ldots n) = 1$且对所有其它次序$\pi$都有$I(\pi)=0$,$I$和$U$之间的距离满足
有了这个定义,我们的例子表明当$k \rightarrow \infty$时,$\|Q^k - U\| \rightarrow 0$。这意味着使用顶端随机插入洗牌最终将产生以相同的概率出现的牌序。
强均匀停止规则
给定一个洗牌技术以及所产生的概率密度函数$Q$,我们希望能够估计经过$k$次洗牌后距离均匀分布多远;也就是说,我们想要知道距离$\|Q^k - U\|$。
强均匀停止规则的概念给了我们了解这个距离的一个工具。首先,假设我们可以观看洗牌序列中的每次洗牌,并想象我们有一个准则,洗牌结果满意时停。
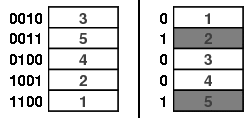
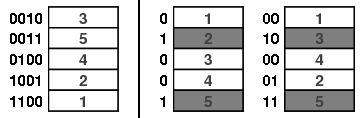
例如,想象我们有一个由顶端随机插入洗牌而产生的序列,当初始时底部那张牌(由n标记)上升到顶部后再被插入牌中某处时,我们停止洗牌。
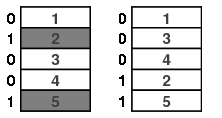
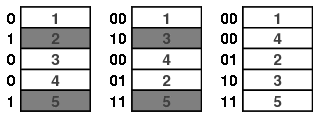
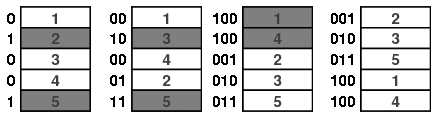
下面我们对n=3的情形说明这一点。在下图中底卡显示为红色,所以我们在达到灰色方块的次序时停止洗牌序列。
如果当洗牌序列经过k次洗牌停下来时由此产生的次序是均匀分布的,那么这样的准则称之为强均匀停止规则。稍稍想一想就能证明,上面所描述的顶端随机插入洗牌规则满足这个条件,因为在每一步后低于牌n下的所有牌的次序是一致分布的。这在上图n=3和k=3的情况下是显而易见的。

为什么强均匀停止规则有用?以下重要的事实给予了解释。
- 假设$T$表示一个洗牌序列的停止时间,$P(T > k)$表示序列停止时间比$k$大的概率。则我们有$Q^k$和$U$之间距离的如下上界:
- \[ \|Q^k - U\| \le P(T > k). \]
换句话说,经过k次洗牌的密度和均匀密度之间的距离比较可以被转移到关于停止时间的分析。正如我们将要看到的,这将是一个简单得多的问题。
上面这个上界来自何处?这个证明是相当直接的。记住距离$\|Q^k - U\|$是通过考察密度在$S_n$的子集上的差异而定义的。用$X_k$表示洗牌$k$次以后的次序,将$X_k$在$A$中的概率按停止时间来分划洗牌的序列
我们将改写上式右端的两项。考虑第一项:这里我们使用的事实是,从一个固定的停止时间后得到的次序是均匀分布的:
使用条件概率改写第二项:
结合这两个表达式给出
上式告诉我们:
因为$P(X_k \in A | T > k)$和$U(A)$都是概率,它们的值在0和1之间。因此,它们的差的绝对值也在0和1之间,因而我们得到
由于这对每一个集合$A$都成立,我们获得所需的上界: $\|Q^k - U\| \le P(T > k). $
浅滩洗牌
有了上面这个工具,我们可以寻找一个强均匀停止规则,研究某种特别的洗牌过程以多快的速度收敛到均匀分布,并确定停止时间超过$k$的概率。我们将把这个工具应用到浅滩洗牌的模式,该模式是一种牌通常的洗牌方式。
若要进行浅滩洗牌,我们根据二项式分布在一副牌的上方选择c张牌。我们选取c张牌的概率是
其中$C^n_c$是二项式系数。我们把这些牌放在左手,其余的n-c张牌则在右手。现在,左手或右手中的一张牌下落的概率与那只手中的牌数成正比。
这个描述建立洗牌物理行为的模型。然而,另一种方法来形容这种洗牌是这样的:根据二项分布在顶部选择$c$张牌。例如,这里我们选c = 3张牌。

现在以相同的概率在$n$张牌的一副牌中选择$c$个位置。

把被选的牌依次序放在这些位置上,其余的$n-c$张牌则依次序放在其他位置。

我们将用$R$表示由一次浅滩洗牌所定义的$S_n$上的概率密度。我们要研究经过$k$次浅滩洗牌后的密度$R^k$,并确定何时它与均匀分布密度足够接近,以此认为洗牌成功。
如果考虑当我们撤消浅滩洗牌时会发生什么,就比较容易回答如上的问题。要做到这一点,只需以相同的概率遍及每一张牌,标签为“0”或“1”。
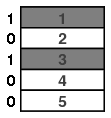
然后依标签将牌分为两个有序组,并将标签为“0”的组放在上头。
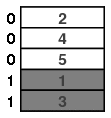
这导致了逆浅滩洗牌:
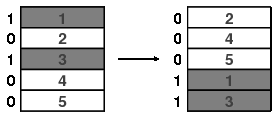
逆浅滩洗牌定义的概率密度$\bar{R}$与原来的浅滩洗牌和均匀分布有相同的距离。要看到这一点,把一个牌序$\pi$看成$n$张牌的一个置换。如果$\bar{\pi}$是逆置换,则我们有$\bar{R} = R(\bar{\pi})$。给定一组置换$A$,我们令$\bar{A}$为$A$的逆置换之集。因此我们有
这个结果意味着$\|\bar{R}^k - U\| = \|R^k - U\|$。
逆浅滩洗牌停止规则
我们已经看到逆浅滩洗牌定义的密度与浅滩洗牌定义的密度和均匀密度处于相同的距离。现在我们想对逆浅滩洗牌建立一个强均匀停止规则。但首先让我们描述枚举逆浅滩洗牌的一种方式。
假设我们进行一系列的k个逆浅滩洗牌。在每个洗牌,每张牌都标有一个“0”或“1”。如果我们连接每个洗牌的标签,则每张牌都标有k个0和1组成的符号串(通常称为k位符号串)。
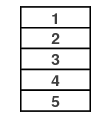
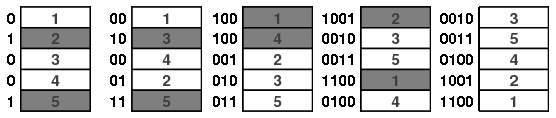
总结一下,k个逆浅滩洗牌的这种序列定义一个n张牌的一个次序以及一组n个k位符号串。反过来,如果选择牌的一个次序$\pi$和一组n个k位符号串,则我们可以定义一列k个逆洗牌:从牌的标准次序开始,基于相应位置的符号来进行逆洗牌:

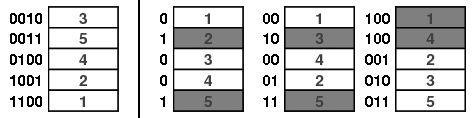


牌最后结果的次序就是$\pi$。
停止规则很简单:牌上有不同的标签时停止。要看到这是一个强均匀停止规则,只需注意到选择一个次序$\pi$和一组$n$个$k$位符号串是相互独立的。因此,如果$B$是一组不同的$k$位符号串,$\pi_1$和$\pi_2$为一副牌的两个次序,则$(\pi_1, B)$和$(\pi_2, B)$给出逆浅滩洗牌的两个可能性相同并分别导向$\pi_1$和$\pi_2$的序列。因此,作为一个逆浅滩洗牌序列$k$时刻停止的结果,我们有和$\pi_1$同样的可能性看到$\pi_2$。
现在,如果$T$是逆浅滩洗牌序列的停止时间,我们可以应用前面的结果:
我们将通过公式($P(T \le k) = 1 - P(T > k)$)计算停止时间大于$k$的概率$P(T > k)$。假设我们有符合$T \le k$的一列$k$个逆浅滩洗牌(如果$T
现在$k$个逆浅滩洗牌序列的总数等于排列$\pi$的个数乘上长度为$n$的$k$位符号串个数,即$n!(2^k)^n$。这给出
这导致估计
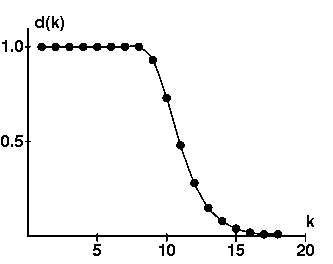
有了这些,让我们考虑用浅滩洗牌法洗有n =52张牌的一副通常的牌。我们发现下述的$R^k$和$U$距离上界,记之为$d(k)$:
|
|
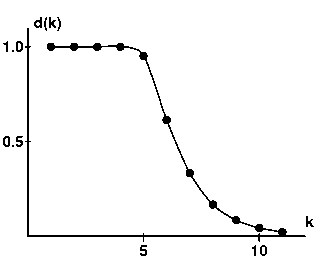
有了这个作为指导,我们可以看到,d(k)对小的k是相对常数,但对较大的k呈指数级下降。必然有一个过渡区域,其中d(k)从大约常数变化到指数衰减。似乎合理的是,这个过渡区域中间的一些k值给出了洗牌的一个适当次数,以保证整副牌已被足够地随机化。使用这个模型,洗k = 12次牌看来是一个很好的建议。
总结
一个更复杂的研究能让Diaconis和Bayer改进这个上界:对n = 52的牌,他们发现
|
|
基于这种分析,Diaconis撰文指出,“七次洗牌既必要又足够让52张牌基本随机。”在本文中,我们的技术仅给出$R^k$和$U$之间距离的一个上界,但J. Reeds 在未发表的一篇手稿中引进了一种技术,找到了一个下界:$\|R^6 - U\| \ge 0.1$。这给予了应采用七次洗牌的进一步的证据。
当然,我们可以用计算机来产生一副牌的随机排序,但我们仍然需要一种可靠的方法,要求计算机给出牌的下一个次序。桥牌俱乐部最初随机互换60张牌;但Diaconis和Shahshahani证明,这不足以产生足够的随机排序。
Knuth描述了一个过程,以i= 1开始,分阶段进行。选择一个随机数$i \le j \le n$,然后互换位置i和j的牌。这产生具有51个互换的均匀分布概率密度。
桥牌俱乐部使用的目前洗牌过程的一个描述由网站Bridge Hands给出。
它是否真的重要吗?是的。马丁·加德纳介绍了一些玩牌技巧,它们基于事实:三次浅滩洗牌不够生成牌的随机排序。例如,假设一副牌洗牌三次,并在每次之后停下来。如果一张牌被取出并被记录,然后放回到这副牌的不同的位置上,则几乎所有的时间这张牌都可被确定。De Bruijn也描述了一个类似的把戏。
我们为浅滩洗牌建立的模型似乎合理,但它如何模拟人工洗牌呢?它依赖于人。研究表明,专业操盘手大约有80%的时间从手中丢下一张牌,约18%的时间丢下一对牌。经验不足的洗牌人只用60%的时间丢下一张牌。当然,当你与孩子玩疯狂八,牌有时会抛向所有的空间,导致只经过一抛就有均匀分布的结果!
后记
这篇文章第一次发表后,一些读者就Diaconis声称7次浅滩洗牌足够随机化52张牌这件事与我联系。这些读者评论的一个很好的总结登载于David Levin, Yuval Peres和Elizabeth Wilmer所著、由美国数学会出版的教科书《Markov Chains and MixingTimes》中第8章结束的附注内。在这个网站http://pages.uoregon.edu/dlevin/MARKOV/上可以看到它:
- 洗七次牌足够充分随机化52张牌实际上对吗?$\cdots$经过七次洗牌,与平稳状态的总变差距离大约是0.3341。也就是说,7次浅滩洗牌后某一特定事件的概率与均匀分布的值的差别可以高达0.3341。事实上,Peter Doyle已描述了一个简单的纸牌游戏,用均匀随机牌玩时赢的概率恰为1/2,但若用标准顺序开始的7次GSR[浅滩]洗牌,获胜的概率为0.801(如在Van Zylen和Schalekamp(2004)中所计算的)。
- 归根结底,对52张牌洗多少次足够这个问题只是一个见解,而不是一个数学事实。然而,存在至少一个人类可玩的游戏,7次洗牌显然是不够的。一个较为合理的水平是总变差距离可能是1%左右,这相当于赌场游戏的赌场优势。这道门槛建议11或12为适当数量的洗牌次数。
- David Aldous and Persi Diaconis, Shuffling cards and stopping times, American Mathematical Monthly 93, 1986, 333-48. 也可在这个网站http://www.jstor.org/pss/2323590上见到.
- Martin Aigner and Günther Ziegler, Proofs from THE BOOK, Third Edition, Springer-Verlag, 2003
- Persi Diaconis, Mathematical developments from the analysis of riffle shuffling, in "Groups, Combinatoricsand Geometry" edited by Ivanov, Liebeck, and Saxl. World Scientific, 2003, 73-97.
- Dave Bayer and Persi Diaconis, Trailing the Dovetail Shuffle to its lair, Annals of Probability 2, 1992, 294-313. 也可在这个网站http://projecteuclid.org/DPubS?service=UI\&version=1.0\&verb=Display\&handle=euclid.aoap/1177005705上见到.
- Martin Gardner, Scientific American, August 1960.
- Persi Diaconis and Mehrdad Shahshahani, Generating a random permutation with random transpositions, ProbabilityTheory and Related Fields 57, 159-79. 也可在这个网站http://www.springerlink.com/content/j602u8m7w061467r/上见到.
- Donald Knuth, The Art of Computer Programming, Volume 2: Seminumerical Algorithms, 3rd edition, Addison-Wesley, 1998.
- N.G. de Bruijn, A Riffle Shuffle Card Trick and its Relation to Quasicrystal Theory, Nieuw Archief Wiskunde 4, 1987, 285-301.也可在http://alexandria.tue.nl/repository/freearticles/597580.pdf上见到.




