旅行售货商的短途环游
我十几岁儿子的课余工作是将报纸投递到148个家庭。当我跟他一起去派报纸的时候,我们会重复地停车、步行到每一家,然后再返回车上。这时一个很自然的问题是,如何选择一条路线使得我们步行尽可能短的距离?
从某个角度来说,这是一个非常简单的任务:共有有限数目的路线,所以我们可以将各种可能的路线全部罗列出来,然后在它们中间搜索到最短的。然而当我们开始去罗列所有路线的时候,我们发现结果是一个巨大的数字:148的阶乘,确切地说,
这看起来像是一个大数目,今天的计算机每秒钟能完成大约十亿次运算,宇宙的生命至今约有$10^{17}$秒。如果我们从宇宙起源时就开始检查这些路线,我们也只能考察大约$10^{26}$种可能性。当然,报纸的读者也不会有耐心等我们以这样的方式找到一个解。
考虑另一个相似的问题。下面是密歇根州中我最喜欢的十个地方:
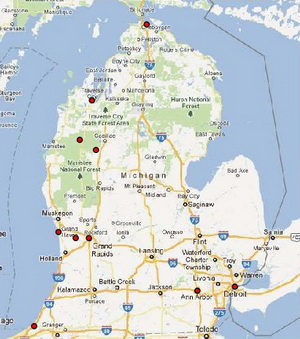
如果希望找到一个最短可能的路线去访问这10个地方,我们将要检查10的阶乘(即1×2×3×4×...×9×10)种可能性。这将导致360多万种可能性来找到这个最短路线。
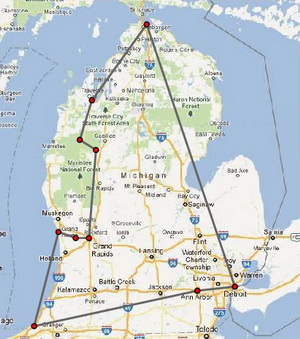
上述问题的关键点是:即使要访问很小数目的站点,不同组合的可能路线的数目也是非常巨大的。直接了当地列出所有的可能性,计算最短路线需要付出相当大的代价,并且在大多数情况下极不现实。
旅行售货商问题
上节的例子都是旅行售货商问题(Traveling Salesman Problem,简称旅行售货商问题)的典型例子。这两种情况中,我们都想用总距离最小的路线去访问一些给定的站点。更一般的情形是,我们希望去选择一条最佳路线,它能最小化某些我们关心的量,比如路线、距离的费用等等。
上节我们已经描述了一种通过考虑所有的可能性来寻找最优路线的方法。但这种方法涉及的可能性太多,导致的计算量大得连超级计算机都不能忍受。另一方面,我们直觉上认为一定会存在一种更好的方法。我和我的儿子就发现了更佳的方法。
事实上,对一般的旅行售货商问题,数学家们至今还没能找到一种通用的寻找最优路线的方法,一般而言这是一个难解的问题。本文中,我们将简单探讨旅行售货商这个有趣问题,并且将描述一个关于它的新结果。
在读完上面描述的两个例子之后,你可能开始寻找你周围的旅行售货商问题的实例。例如,你将用什么样的方法去安排你的一天呢:去工作,去杂货店,去学校接送孩子,去咖啡店。你可以设想邮递服务,比如快递公司,当安排包裹的日常收取和递送时,将面临最短路线这个问题。美国总统选举时,候选人要去多个州参加政治竞选活动,当他们在爱荷华州参加竞选活动时,竞选班子总是试图去使花费最小,而最大化他们候选人的曝光率。
William Cook的精彩新专著“In Pursuit of the Traveling Salesman”描述了旅行售货商问题的很多实例,这个问题源于一个旅行售货商访问一些城市去销售某个公司的产品。另外,他解释了许多最新的应用,包括建立望远镜有效运用时间的时间表,研究基因图谱新方法等。

作为另外一个例子,在生产某些数字电路板时,需要钻孔成千上万个,使得电子元件(如电阻和集成电路等)可以嵌入其中。钻这些孔的机器必须尽可能有效地去访问电路板上的每个相应位置。如何选择最佳路线又是一个旅行售货商问题。
显然本文讨论的问题是普遍存在的,我们希望有一个好的求解方法。
多好才是好?
本文第一节说n个节点的所有可能路线共有n的阶乘个,即$n!=n\times(n-1)\times(n-2)...\times3\times2\times1.$即使是对适当的$n$,这也是一个大的不可能处理的数字。送报纸到148个家庭就导致了天文数字的路线。而考虑电子电路板上的成千上万个孔时,这个问题自然就难上加难了。
数学家们已经发展了一种方法来评估一个问题的困难程度,即求解该问题的算法复杂性。一般而言,复杂性是一种工具,用来衡量根据给定数目(我们将称这个数目为$n$)的函数来解决一个目标问题所需做的努力。例如,我们之前讲到的求解送报纸路线的蛮力算法的复杂性,通常被记为$O(n!)$,即我们粗略地认为它跟$n$!成正比例。
再举一个例子。你希望在电话簿中查询一个号码,做这件事的一种方法是在整个电话簿中寻找,一次一个条目,直到找到你所期望的。这里的努力是跟电话簿的条目数$n$成比例的,所以我们说这个算法的复杂性是$O(n)$。如果电话簿的大小翻倍,那么我们大概要做两倍的工作。
当然,存在一个更好的算法来寻找电话号码,即二分搜索算法,简称二分法。如果电话薄是以姓氏笔划排序的,你可以在电话簿的中间打开它,确定你要找的条目的姓氏笔划在此之前还是之后。比如在前一半,则把前一半的中间打开再确定你的目标条目是在上一半还是下一半,在后一半时也是同样处理。然后重复做下去。这里需要的努力是$O(\log(n))$,大概与以2为底的$n$的对数成比例。这种情况下,如果电话簿的大小翻倍,你只需要多做一步。显然这是一个更好的算法。
注意到复杂性的这种衡量是与解决问题的算法相关的,而不是与问题本身相关。
再考虑一个裤子衬衣问题。假设你有裤子和衬衣各$n$件,当你早上穿衣服的时候你要考虑所有可能的组合。因为总共有$n^2$种组合,需要的努力是$O(n^2)$。如果$n$翻倍,我们需要做大约四倍的工作。
我们现在定义一个很重要的问题类,称为$P$类。如果存在一个解决问题的$O(n^k)$的算法,其中$k$是某个整数,那么这个问题属于$P$类。这里的$P$代表“多项式”,运行算法所需要的努力与$n$的某个多项式成正比。
我们通常认为$P$类问题是“简单的”问题,即使相应的指数$k$是一个非常大的数。而旅行售货商问题的蛮力算法的复杂性是$O(n!)$,如果我们将$n$增加1,我们需要做$n$倍多的工作,这个工作量的增加是非常恐怖的。
到目前为止,我们不知道旅行售货商问题是否在$P$类中,换言之,没有已知的算法能以多项式的复杂性来解决一般的旅行售货商问题。但这也并不意味着明天不会有人找到一个这样伟大的算法。
另一个问题类被称为$NP$:如果一个可能的解可以用一个多项式时间算法来验证,则这个问题属于$NP$。换言之,解的验证算法是$O(n^k)$,其中$k$是某个整数。
一般来说,验证一个可能的解要比找到解更容易。例如,寻找231832825921的素数因子是富有挑战的问题,而验证233021乘以994901等于231832825921是相对容易的。我们可以验证$P \subset NP$。换言之,如果我们可以在多项时间内产生问题的解,那么我们就可以在多项式时间内验证我们有一个解。
令人惊讶的是,我们并不知道旅行售货商问题是否在$NP$内!考虑欧氏旅行售货商这一特殊情况:这时站点取自欧氏空间,访问站点间的费用是欧氏距离。如果我们固定一个常数$K$,我们可以问一条路线的距离是否小于$K$。这看起来像是一个简单的问题,回答它需要计算一些平方根,然而没有已知的多项式时间算法来确定一些平方根的和是否小于$K$!
鉴于此,这吸引我们去思考非常特殊的$P$类问题,事实上,我们并不知道那些不属于$P$类的问题。已知的问题里我们也不知道属于$NP$类但是不属于$P$类的问题。因此,人们自然地要问是否$P = NP$?这是数学中一个重要的数学难题,是克莱数学研究所设立的每个价值百万美元的六大难题之一。
最后一类问题是$NP$完全问题:一个问题属于这个类,如果$NP$中的任何一个问题都可以在多项式时间内归结到这个$NP$完全问题。尽管我们不知道旅行售货商问题是否属于$NP$,然而引人注目的是,它确是一个$NP$完全问题。因此,如果你可以发现一个旅行售货商问题的多项式时间算法,那么我们将知道$P = NP$。进而你将获得100万美元。
在2002年举办的一次调查中,Bill Gasarch询问一组专家他们是否相信$P = NP$。61人认为这是不正确的,只有9人相信这是正确的。另外,大部分人相信需要很长一段时间才能等到水落石出的一天,并且彻底解决这一问题将需要全新的思想。你可以在这里看到调查的结果。
我们很容易相信$P \neq NP$:我们的经验是通常情况下,测试一个可能的解比寻找解要容易得多。因为算法研究的历史要短些,人们有理由相信,随着这一领域的成熟,我们将发现一些基本的新技术,它们也许能证明这些任务需要同样多的努力。
我们所知道的
看起来旅行售货商问题是一个很难的问题,虽然我们目前不能百分之百地确定。更糟糕的是,可能会在很长一段时间里,答案也不能揭晓。与此同时,关于这个问题我们能做什么呢?
除了$O(n!)$这个蛮力算法,目前我们的最好算法是1962年Held和Karp发现的一个$O(n^2\cdot2^n)$的算法。注意到它的复杂性是指数的而不是多项式的,并且这一结果在过去50年的时间里一直没有被改进。
然而,人们还是在不断提出新的方法来攻克旅行售货商问题,这也促使人们不断地去寻找基于较大站点集合的最优路线。1954年,Dantzig, Fulkerson和Johnson用线性规划的方法在美国当时所有的48个州以及哥伦比亚特区的主要城市中找到了最短路线。从那时起,人们在3038个城市(1992年),13509个城市(1998年),85900个城市(2006年)中找到了最优路线。这些计算中用到的某些计算机代码被称为Concorde,它可以免费得到。
一个惊人的例子是,在十万个站点中一个几乎最优的旅行售货商问题的路线,居然可以被用来重构达芬奇的蒙娜丽莎。
记住一般的旅行售货商问题是用不同站点间旅行费用的度量来定义的。一般的旅行售货商问题是很难解决的,但是对它的某些特殊情形是可能存在好的算法的,例如,欧氏旅行售货商问题也被认为是NP完全的。所以我们现在将着眼于欧氏旅行售货商问题的一个结果,希望它能将$P = NP$的问题更清楚地显示出来。
多项式时间近似方案
如果一个工作太难完成,我们会寻求近似地完成它。也就是说,如果不能找到绝对最短的旅行售货商问题的路线,也许我们可以去寻找一条路线使它不长于最短路线的10%或5%。
1976年, Christofides发现了一个多项式时间算法可以用来产生一条路线,它不长于最优路线的50%。然而引伸的问题是:如果我们固定一个误差,是否可以找到一条路线,使它的长度与最短路线的差控制在给定误差以内。
上世纪九十年代,Arora和Mitchell独立地发现了在多项式时间内给出欧氏旅行售货商问题近似解的算法。Arora发现了这样的算法:对给定$c>1$,可以找到一条路线,它的长度不超过最短路线的$1+1/c$倍。他的算法的一个随机形式的复杂性是$O(n(\log n)^{O(c)})$,这也是我们将要描述的。
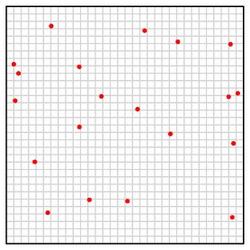
Arora的算法应用动态规划中称为四叉树(quadtree)的数据结构。开始时,考虑我们要去访问的欧氏旅行售货商问题中的站点并把它们放在一个方格中。

现在,让我们来关注这个方格,并将它剖分成四个方格。
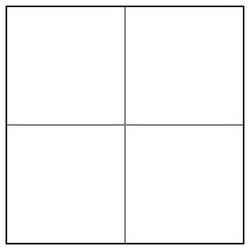
继续这一过程将产生一棵四叉树,树中的每个点都是一个方格,每个内部点都有四个孩子。树的根点是一个内部的方格。
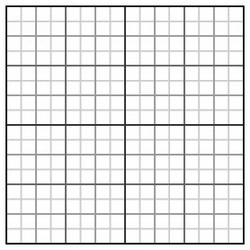
现在我们可以开始描述Arora的发现旅行售货商问题近似解的算法。我们固定数$c$,并寻找一条路线,它的长度不超过最优路线的$1+1/c$倍。例如给定$c=10$,那么我们将发现一条路线,它的长度不长于最优路线长度的10%。
我们将构造一棵四叉树,使得它的每个叶子点只包含我们旅行售货商问题中的一个位置。如果两个位置非常接近,我们的树将需要降到相对比较深的小树来寻找将这两个点分开的正方形。为了避免这种麻烦,我们将轻微地干扰这些点:如果最初的大方格的边长为$L$,那么我们将构造一个宽为$L/(8nc)$的网格,并且将每个位置移动到离它最近的格点上去。
 |
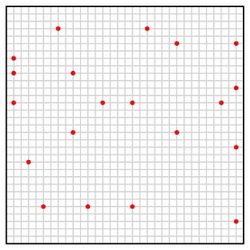 |
我们观察到两点:假设$OPT$是最优路线的长度。因为$L$是初始盒子的边长,我们有$OPT\geq 2L$。另外,注意到每个点移动的距离小于$L/(8nc)$,这意味着每条路线的总长度将会改变至多$2n\cdot L/(8nc)
尽管两个站点可能被移动到同一个格点,但是我们将保证两个站点可以以至少$L/(8nc)$的距离被分开。通过剖分其中多于一个点的方格,我们现在构造一棵四叉树。
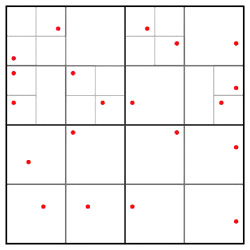
由于我们的扰动,现在四叉树的深度是$O(\log n)$,所以四叉树中方格的个数是$T=O(n\log n)$。
我们可以通过平面的尺度变换来假设站点具有整的坐标。这并不影响路线的相对长度,并且稍后我们还可以还原它。
下面我们将描述一个动态规划的算法来找到我们的旅行售货商问题的一个近似解。在每一个方格中,我们将限制进入这个方格的路线上的那些点。最后,我们在区间$[c\log L, 2c\log L]$中选择一个整数$m$,它是2的幂。在每个方格的边上,我们均匀的放置$m+1$间隔点,称为门(portal)。
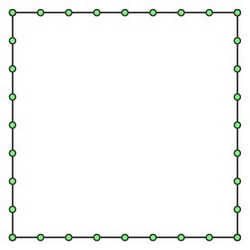
引入门这一概念的动机是,我们只需要检查进入某个方格的路线上的相对少的位置。而门越多,我们的路线就越接近最优路线。
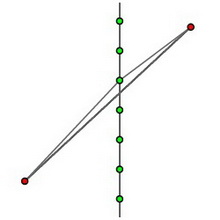
因为$m$是2的幂,一个内部点的门也是由它生成的每个孩子的门。
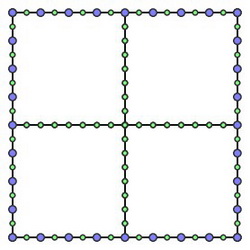
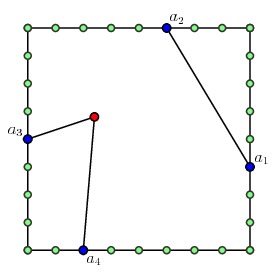
我们现在在每个方格上考虑由门的集合$a_1$, $a_2$, $a_3$, ..., $a_{2p}$构成的多路径问题。我们要去找到一些最短路线的集合:连接$a_1$到$a_2$的路, $a_3$到$a_4$,等等,并且去访问方格内部的每一个旅行售货商问题的站点。
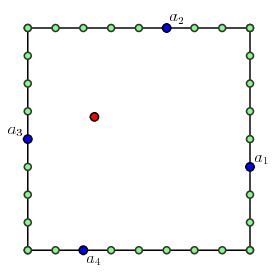
对叶子点来说,这是一个相对简单的问题:我们列出所有可能的路,在其中寻找最短的。对上面的问题,只有如下两种可能性以及最短路的集合,多路径问题的解是右边的那个图。对每一个门的集合$a_1,a_2,\ldots, a_{2p}$,我们保持这个解的一个记录。
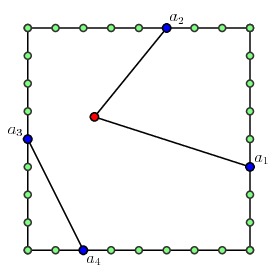 |
 |
对内部点,我们有如同这样的多路径问题:
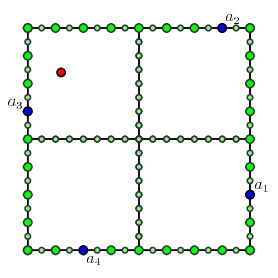
假设我们已经解决了所有可能的孩子的多路径问题。这时要解决内部点的多路径问题,我们考虑内部边上每个可能产生多路径孩子的门的选取。
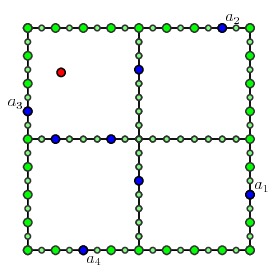
现在我们寻找孩子的多路径问题的解,从而构造父母点的多路径。
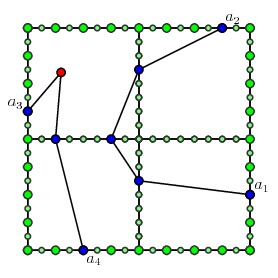
这样,我们仅需搜索内部边上所有可能的门的选取,以便寻找父母点的多路径问题的解。
我们沿着树寻找直至到达根点,当边界上没有门时我们就解决了多路径问题。这给出了一条路线,它给出了一个旅行售货商问题的近似解。
要估计运行这个算法所需计算的努力,我们需要记得在四叉树中共有$T = O(n\log n)$个方格。细心一点,我们可以列举我们要解决多路径问题所要的门的选择,这将给出Arora的算法复杂性$O(n(\log n)^{O(c)})$的估计。
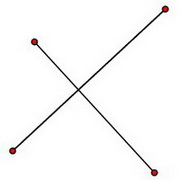
我们找到的路线可能会有一些交叉,但是我们可以在不增加路线长度的情况下消除这些交叉。
 |
 |
不幸的是上面叙述的算法有可能找不到一条路线,使它和旅行售货商问题的解相差到给定的精度。例如,当路线在四叉树中交叉很多次的时候,就有可能发生。
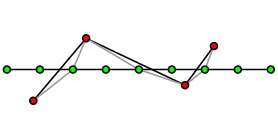
因此,Arora引入了一种转换的四叉树,在需要的时候转换四叉树中的方格并允许它们有一定的环绕,见下图。
 |
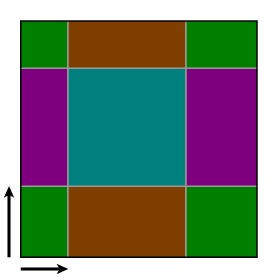 |
Arora分析了这些转换对算法生成的路线与方格的边的交叉次数的影响。该分析显示如果一个转换是随机选取的,那么算法找到一条长度小于$(1+1/c)OPT$的路线的概率至少为1/2。
为了保证得到一条在误差值范围内的路线,我们可以尝试每一个可能的转换,并且仅取相应得到的路线中最短的那条。假设站点具有整的坐标,我们只需要考虑$L^2$个转换,这样运行时间增加了$L^2=O(n^2)$的倍数,因此算法仍然可以在多项式时间内完成。
总结
因为Arora的算法的执行并不是特别地有效,所以我们应该主要将这个结果视为一个理论上的结果。
前面提到的欧氏旅行售货商问题是NP完全的,这意味着如果可以找到一个解决欧氏旅行售货商问题的多项式时间算法,那么$P = NP$。Arora的结果并不能证明这一结论,但它告诉我们,可以用一个多项式时间算法以任意要求的精度来逼近最优路线。问题是精度要求越高,相应的努力就越大。
为了表彰Arora和Mitchell在这一问题上的重要贡献,2010年度计算机协会的哥德尔奖(Godel Prize)被授予了他们。
参考文献
- Sanjeev Arora, Polynomial Time Approximation Schemes for Euclidean Traveling Salesman and other Geometric Problems, Journal of the Association of Computing Machinery, 45(5), 753-782.
- Joseph S.B. Mitchell, Guillotine subdivisions approximate polygonal subdivisions: A simple polynomial-time approximation scheme for the geometric TSP, k-MST, and related problems, SIAM Journal of Computing, 28(4), 1298-1309.
- William J. Cook, In Pursuit of the Traveling Salesman, Princeton University Press, 2012. Written in an engaging, personal style, this highly readable book includes a great deal of history and anecdotes surrounding the TSP as well an introduction to techniques and results.
- E.L. Lawler, J.K. Lenstra, A.H.G. Rinnooy Kan, D.B.Shmoys, The Traveling Salesman Problem, John Wiley & Sons, 1985.
- David L. Applegate, Robert E. Bixby, Vasek Chvatal, William J. Cook, The Traveling Salesman Problem: A Computational Study, Princeton University Press, 2006.
- The Traveling Salesman Problem. This site, maintained by William Cook, will be of use to anyone interested in the TSP.




