引言

作为一门学科，数学有简朴之美的声誉——它对某些人产生共鸣，就像美丽的日出日落、动听的交响乐或漂亮的图画可能对其他人产生共鸣一样。然而，数学也有其应用的一面。如果没有20世纪发展的数学，我们不会有正在从根本上改变我们21世纪初生活方式的手机。与数学的美感及适用性双重背景相比较的是这样的感觉：数学前沿与非数学使用者能掌握的东西越走越远。数学证明已经变得越来越长、越来越复杂，并且在某些情况下，重要定理已经整体上需要计算机的帮助。这方面的例子有Wolfgang Haken和Kenneth Appel计算机证明了四色定理这一猜想以及Thomas Hale计算机证实球体可以挤进三维空间并能达到最大密度。

由于许多数学家的工作以及他们对数学的热爱，以及清晰的洞察，使我们可以更清楚地看到数学的美感与适用性这两方面。在这方面做出杰出贡献的数学家很多，在这里，我想介绍前几年去世的美国几何学家Victor Klee的工作。

Victor Klee是美国最杰出的几何学家之一。他的去世（2007年8月）是数学界的重大损失。他出版的作品包括几本书和超过240篇的研究论文。Klee于1925年出生在旧金山，在Pomona学院修了数学和化学两个专业。虽然20世纪之前，几乎所有的数学家（如牛顿、高斯、欧拉、拉普拉斯等）不仅在数学，而且在物理或一些其他科学分支均有贡献，但由于专业化的压力，现在这很难得了。虽然Klee的工作大部分集中在几何上，出于理论与应用的考虑，他的工作横跨的兴趣广泛。他在弗吉尼亚大学跟随著名的拓扑学家Edward McShane学习，获得博士学位。他1949年的博士论文题目是“线性空间中的凸集”。

Klee的早期训练和研究是在拓扑学领域——这个学科关注几何对象属性的研究，它超越了角度、距离和与欧几里得几何有关的领域的传统。因此，从拓扑的观点看，直线段和曲线段是一样的，正方形和（欧几里得）椭圆也是一样的，但线段和圆不是一样的。这种拓扑意义下的区别意味着一个圆圈把平面分为内部区域和外部区域，而线段则不能。因此，如果在平面上取不共线的两个点，则可以找到连接这两点的一条曲线，它与该线段没有共同的点。然而，对于圆内一点和圆外一点，连接它们的任何曲线和圆必有一个共同点。这是拓扑学家感兴趣的一种几何信息，而不需要关于距离的信息。

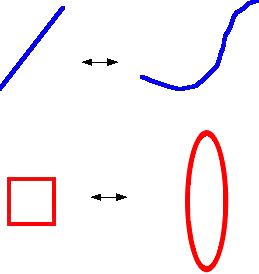图1：几何集可以看起来不同但是拓扑等价。

Klee职业生涯的大部分时间都是在华盛顿大学（西雅图）度过的；他1953年去那里教书，2000年从那里退休。在华盛顿大学的岁月里，他指导了34个博士生，其中大部分将自己说成是几何学家。他的学生们进而也已经训练出许多其他的几何学家。根据“数学家谱名册”，Klee有100个数学后代（他也有“正规的”孩子及孙辈）。Klee在华盛顿大学的大部分时间里，另一个突出的几何学家Branko Grünbaum也在那里。Klee和Grünbaum同处一地的30年时光使得华盛顿大学成为一个不断发展的新型几何中心。Klee从1971年至1972年担任美国数学会的会长。他对组合学、凸性、算法及优化问题作出了贡献，但他的工作始终有一个强烈的几何风味。要充分认识Victor Klee在最近的几何演变过程中所占的位置，有必要先讲点题外话来简短地看一看几何从古代到近代的演变。

什么是几何

在20世纪的初叶，几何的研究处在一个十字路口上。19世纪末，不仅从数学而且从一般知识的观点中，几何的世界被思想史上的伟大里程碑之一所震撼。

大部分历史中的几何研究支柱一直是欧几里得的《几何原本》。这本书自从出世就已经历尽众多的版本和若干语言的翻译。尽管我们对欧几里得这个人知之甚少，并且没有这本书可以追溯到甚至接近欧几里得生活过的时代的版本，《原本》一直是几何演变的中心。两千年来，《原本》的内容不断让数学保持活力，并激励了许多人成为数学家，特别是几何学家。《原本》中有许多漂亮的结果，包括5个正多面体和素数的讨论。称为欧几里得算法的寻找两个正整数最大共因子的开创性算法，也可以在那里找到。欧几里得著名的第五公设是：

“如果与两条直线相交的一条直线同一边的内角之和小于两直角，则这两条直线，如果无限延长的话，将在满足上面条件的那一边相交。”

对许多人而言，这似乎比其他公理更为复杂，人们试图使用其他公理通过逻辑法则来证明这个公理。直到19世纪后期人们才认识到这些努力注定要失败。这项工作是由高斯、鲍耶、罗巴切夫斯基作出，但只有后两位发表了他们的研究结果。所出现的是激动人心的一些几何。它们通常被称为“古典非欧几何”，它们由把第5公设修改为“不存在通过给定的$P$点与直线$m$平行的直线”或“存在许多通过给定的$P$点与直线$m$平行的直线”而诞生。经典非欧几何之一是射影几何。你可以把这个几何视为起始于3维欧氏空间中的一个球面。“新”几何如何解释未定义的术语“点”和“线”？在“新”几何中，一个点将与球面直径的两端点等同起来，也就是说，如果$P$和$P^*$是一条直径的两端点，则把集合$\{P, P^*\}$看作一个点。“新”几何的线将是球面上中心为球心的圆。现在很容易看到，这些点和线的定义导致“两点确定一线”和“两线交于一点”的结论，因此，我们有一个没有平行线的几何。

下面的图示可以帮助你直观了解双曲平面或鲍耶-罗巴切夫斯基平面的某些方面，这是另一传统的非欧几何。它被称为凯莱-克莱因模型，因为数学家阿瑟·凯利和费利克斯·克莱因的研究之故。如果点和线未定义，我们可以如下解释这两个术语。一个点将意味着圆内任何一点，如图2所示。一根线将意味着圆的任何弦（不包括边界点）。因此，图中的线$m$由弦上的点组成，但为了我们的目的，弦位于圆周上的两个终点将被“删除”。现在，你可以看到，如果点$P$不在$m$上，则有很多甚至无穷多的弦经过$P$点且和弦$m$不相交。这样，我们有无穷多个通过$P$点与不包含$P$点的线$m$平行！

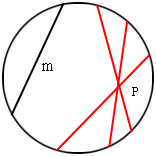图2：一个几何模型和许多线平行于给定线穿过一个点。

非欧几何的发现在哲学界以及数学界造成了某种“危机”。由于从数学的角度看射影几何和双曲几何都同等立足于欧几里得几何，什么是物理空间的真正几何这一问题出现了。也许我们生活的空间不是欧几里得的版本！（在欧几里得几何里平面三角形的内角和等于180度，而在球面几何中它们的和超过180度，在双曲平面里小于180度。它也提出了几何的研究应采取什么样的方向的问题。相对而言，双曲平面的研究比欧几里得几何更需精致。数学教育工作者面临着多少注意力应该投向于新几何的问题（在此期间有限几何也得到发展）。随着澄清了欧几里得的“疏忽”并为欧氏几何提供了一个独立的公理集合（即没有公理可由其他公理证明）的希尔伯特公理体系的发表，几何似乎在某些方面“失去势头”。在几何研究的低潮时期，一定程度上重振几何雄风的是杰出的几何学家Harold Scott MacDonald Coxeter.

Coxeter是传记《拯救几何的人》的主角，他属于成长于19世纪几何的那部分人。他的工作强调了几何的度量（距离）和公理方面。纵观一生，他充当着过去（19世纪及更早）的几何和20世纪几何学家涌现的新兴趣之间的“桥梁”。Coxeter也作出了几何和代数之间的连接。特别是，他发现了使用群理论和对称性思想的力量来得到关于几何问题的洞见。Coxeter探索过包括高维多面体的许多问题。这项工作涉及到非常对称的多面体，是欧几里得曾经研究过的著名的五个正多面体（柏拉图立体）的类似物。比Coxeter小18岁的Klee将全力遵循“几何传统”，但带有与Coxeter非常不同的兴趣点，部分地缘由他在拓扑方面的训练。

Klee的数学

Klee的数学贯穿于几何的许多方面。下面，我想提请注意Klee参与的三个重要成果，它可以用初等术语讨论：画廊定理、Klee-Minty多面体和Kleetopes。我们先品尝几样东西，显示他对理论和应用数学论题兴趣交融。他对凸多面体的理论作出了特别重要的贡献，尤其是高维空间的多面体。一个多面体是一有界凸集，它是平面的高维类似物的交集。（注：如果对一个集合中的任意两点$p$和$q$，连接$p$和$q$的线段也在集合中，则该集合称为是凸的。）

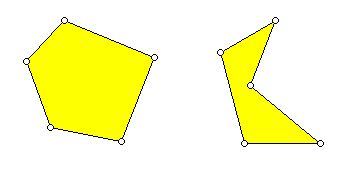图3：凸五边形(左)；非凸五边形(右)

多面体理论虽然从理论数学的角度来看属于理论领域，但它与应用数学有着戏剧性的连接。

线性规划

二战期间，大批的男性和大量的材料必须从美国转移到欧洲和太平洋战区。经过大萧条阵痛的美国，改装工厂制造战争物资，而不是消费类产品。数学的一门新的子学科，运筹学或管理科学，在战争结束后出现。这项工作根植于为赢得二战胜利而找到的一些数学工具。（数学在战争中的另一胜利是破译德国和日本的密码。）二战结束后，生产管理、调度、成本最优化等大型问题在政府和企业中变得越来越重要。

这个新数学分支的基石成为众所周知的线性规划。一个典型的线性规划问题可能涉及到如何从不同种类的原油生产出不同类型的汽油。其想法是，每个产品的生产需要一定数量的原材料。此外，一定数额的原材料以不同的成本可以获得。这个过程的的目标是以最小成本从现有的原油供应生产所需汽油。类似的问题数学上可以表达成在一个线性不等式系统约束下找到一个线性表达式的最小值或最大值。如下显示一个线性规划的“婴儿”问题，让你看一看它的数学术语像什么：

其中

且

上述不等式对应于2维空间中某个多边形中的点（在下面图4中以红色显示；你能找到$G$点的坐标吗？）。更一般的问题通常有数百个变量，也许有数千个约束。这些问题导致多边形概念在高维空间的推广问题。这些就是称为多面体的对象。满足这些约束条件的点原来是一个高维多面体上面或内部的点。然而，值得注意的是，可以证明这样一个问题的最优解总可以在“可行”多面体的某个顶点达到。在图4的多边形中有4个顶点，我们可以限制于此，以确定满足约束的所有点的最大值发生在何处。给出这个结果的定理有时也被称为角点定理。叙述这一结果的另一种方式是：不必检查无穷多点求出最优（最佳）解，仅仅检查有限多个角点，看最好的解在哪个点出现就可以了。

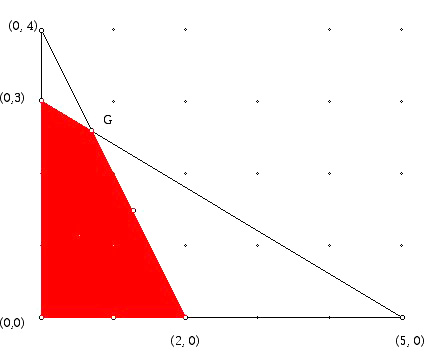图4：分它满足一个线性规划问题的内容

为了解决大型线性规划问题，人们使用称为单纯形算法的一个工具，它由美国数学家George Dantzig在二战结束后不久发明的。单纯形算法使得求解大规模生产、资源分配、调度和产品制造问题成为可能。然而，尽管该算法似乎能用合理的电脑时间来解决大型问题，当时还不清楚算法的理论复杂性是什么；即当线性规划问题用变量和约束的数量来衡量的规模越来越大时，需要多少电脑计算量来求解这些问题？单纯形法的工作方式是，它首先找到一个可行点，即满足给定约束条件的点。假设我们正试图求解的线性规划问题是一个最大化问题。我们寻找变量的值使得某个线性函数（称为目标函数）的对应值尽可能地大。从这个可行点开始，算法选择可行多面体上与目前顶点以边相接的一个相邻顶点，检查该点目标函数值是否不减。最终可以到达一个点，使得目标函数在所有邻点上的值都没有比当前值更大，也就是说当前值就不能被改善。Victor Klee在帮助建立线性规划的应用世界和多面体理论的理论景观之间的连接方面起了关键的作用。

他这方面的工作就是现在所谓的Klee-Minty多面体，与George Minty的合作成果。Klee的许多论文来自于他对线性规划问题的兴趣。如上所述，线性规划是一个离散的优化模型，其目标是最大化或最小化变量在某个凸多面体内取值的一个线性表达式。由于线性规划问题出现在各种各样的情况中，包括资源分配、调度和混合，当问题的规模非常大时，采用单纯形法需要多少计算时间变成一个有趣的问题。尽管在实践中能快速求解问题，没有理论证明对于大规模问题的计算工作量是以小于多项式的方式增长的。Klee和Minty通过例子证明，对某些问题，单纯形法可能需要指数量增长的时间求解。他们巧妙的构思是修改一个非常对称的高维立方体结构，比如说$d$-立方体（有$2^d$个顶点）。下面的图显示了一个4维的立方体。

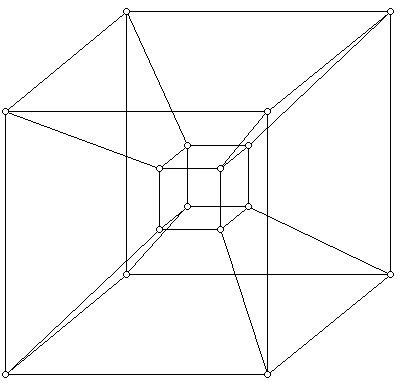图5：4-cube的示意图

通过选择$d$-立方体的一个合适变形，Klee和Minty证明，从一个特定点开始的单纯形算法将跑遍$d$-立方体的所有（这是指数级别的大数$2^d$）顶点才到达目标函数取最优值的那个顶点。这意味着单纯形算法沿着一条“哈密尔顿路径”行进（也就是说，当路径通过$d$-立方体的所有顶点时，路径的第一个和最后一个顶点不必由一条边相连）。这族例子现在已为Klee-Minty立方体。Klee-Minty例子表明，实际中的线性规划问题似乎没有像需要指数级工作量多面体那样的可行区域，因为在实践中单纯形算法运行很快。这项工作来自于Klee关于高维多面体路径结构的理论工作，展示了数学中的理论和应用想法可以相得益彰。直至今天，Klee提出并为之工作过的关于多面体直径的一些问题（如$d$-多面体的顶点相距多远），仍然没有得到解决。

总之，Klee和Minty所做的是构造一族多面体，其顶点的个数关于维数呈指数增长，并且当单纯形法应用到这些多面体上的线性规划问题时，然而该方法需要造访多面体的所有顶点才能达到最优值。这族例子表明，单纯形算法可能需要指数增长的工作量。现实世界中的线性规划问题从来没有见到过这么大的工作量，其中的原因尚不完全清楚。在实践中，大型线性规划问题通常采用单纯形法很快求解。这使得世界各地的政府和企业生活得更轻松！

Kleetopes

早在多面体的历史之初，多面体是否有一个包括其所有顶点的简单闭回路的问题，即哈密顿回路问题，一直是数学家感兴趣的。这种兴趣部分源于这样一个事实：至少有三条边与某点相连的凸多面体如果有一个哈密顿回路，那么它的面可以用4种颜色着色。看到这一点的方式是3维的凸多面体可以画在平面上。一旦有这样一个“平面”绘画，如果这个图$P$有一个哈密顿回路（由$P$的顶点和边组成），则将约当曲线定理用于哈密顿回路，图内图外均有面。现在可以分别用2种颜色着色内部和外部的面。下图显示了一个典型的例子。注意此图中有一蓝绿色特殊面，它围绕所有其他面。哈密顿回路以粗黑边显示。哈密顿回路内的面所用的两种颜色是红色和绿色，而哈密顿回路外的面所用的两种颜色是蓝色和蓝绿色。

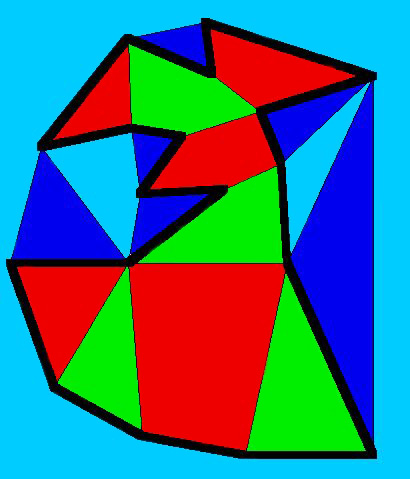图6：在飞机上画一个图，其中用4种颜色为哈密顿回路地区上色。

（事实证明，处理四色问题的这种方法不奏效，因为存在非哈密顿3-价多面体，第一个这样的例子属于W.T. Tutte。）Klee自然有兴趣问高维多面体是否总有哈密顿回路。这部分是因为他对线性规划问题以及与多面体路径相关的理论问题的浓厚兴趣。使用一个非常简单的想法，他证明了：对每一维数存在非哈密顿多面体。他的想法在3维情形可用称为“Kleetope”的思想来说明。

从一个所有面都是三角形的多面体开始。图7给出了这样的一个例子。

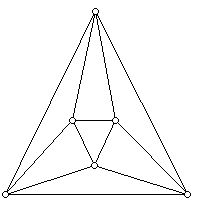图7：三角形面多面体图

该图是正八面体的图。注意它有6个顶点和8个面。因此，多面体有比顶点更多的面。Klee建立一个非哈密顿多面体的方法是在这个多面体的每个面上竖立一个金字塔。构造在图8中进行。

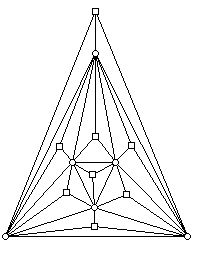图8：在图7多面体的面孔上绘制的金字塔。这个新的多面体被称为作为Kleetope。

图7中原来的顶点用小圆圈表示，金字塔“尖顶”的新顶点用小正方形显示。注意此图不是一个二分图。（二部图的顶点可用两种颜色着色，使得任一边两端的顶点有不同的颜色。）然而，正方形的顶点仅仅联接到圆圈标记的顶点，但圆圈标记的顶点联接到圆圈标记的顶点和正方形标记的顶点。上图不能有一个哈密顿回路，因为要到达一个正方形的顶点，必须从一个圆的顶点而来，但没有足够多这样的顶点与正方形的顶点形成一个简单的回路，因为最初的多面体有比顶点更多的面。上述图是一个组合图，对于它Steinitz定理保证了图可以由一个凸三维多面体实现。然而，为此目的不必调用Steinitz定理，如Klee所观察到的。假设在图7中挑选多面体的一个特别三角形。如果在这个面内部的上方选择一个点非常靠近这个面，然后这个面上的“平”的金字塔不会破坏所产生的新的多面体的凸性。这个过程可以对图7中原先多面体的每个面依次进行，直到得到一个和图8有同一个图的多面体。

类似的想法在$d$维同样可以进行，这时没有Steinitz定理的类似物成立。因此，Klee的简单想法使人们可以看到如何构造高维的非哈密顿凸多面体（及它们的图）。这促使人们有兴趣问具有更强性能的高维多面体是否总有哈密顿回路。例如，Victor Klee的博士生之一David Barnette的一个悬而未决的问题涉及4维多面体的哈密顿回路。一个$d$-维的凸多面体被称为是简单的，如果它每一个顶点都是$d$价（阶）的。因此，一个简单的3维凸多面体将有3价，而一个简单的4维凸多面体有4价。虽然存在3价的非哈密顿简单3维多面体（最小的例子有38个顶点），David Barnette曾提出猜想，每一个简单的4维凸多面体有哈密顿回路。它仍然是一个未决问题。Klee的遗产依然活在他学生的几何工作中！

画廊定理

在这三个卓越成就中，Klee在“画廊”定理的发展中所发挥的作用时间上是最近的。1973年，年轻的捷克数学家Vasek Chvatál挑战Victor Klee描述初等几何中一个“有趣”的问题。Klee以下面的问题回应。

假设我们有一个平面$n$边简单多边形。这个多边形可以被看作是银行、博物馆或画廊的平面图。我们想在多边形的一些顶点处放上传感器，使得它们可以集体看到或守卫博物馆的所有内部点。多边形内部的一个点$p$被说成可从多边形的顶点$v$可见，如果线段$pv$不包含多边形外面的点。（这个条件是不太现实的。这意味着，一个点$p$可以从顶点$v$可见，即使从$v$到$p$的线段包括许多孤立的顶点或多边形边界上的一段。然而，这样来形容问题数学上是方便的。）

虽然Klee有一个猜想，即存在一些$n$边形需要$[n/3]$（$n/3$向下取整，所以$[5/3]=1$）个顶点守卫，并且没有$n$边形需要超过$[n/3]$个守卫，他却不能证明它。Chvatál第一个证明了这个猜想，但是Steve Fisk提供了一个真正优雅的方式来看到事情的原委。

这个问题的一个常见误解是，被要求的是一种算法，它对于一个给定的固定多边形$P$找到多边形$P$守卫顶点的最小数目。这显然是一个有趣的和重要的问题。然而，不幸的是，求解这个问题所有已知的算法都需要作为多边形边数$n$的函数指数级的工作。更确切地说，已经知道这个问题是NP完全问题。这意味着不可能有一个多项式时间算法找到一个固定多边形$P$守卫的最低数目。

Victor Klee有找到简单想法、例子和问题的天赋，可以直捣几何和组合问题的核心。他的探究精神，改变了几何的方向，同时不可估量地丰富了几何和数学。