复数计算与几何证题
同学们在代数课程中学习复数这一部分的时候,一般对复数的代数演算注意得比较多,而对这种数及其运算的几何意义注意得比较少。其实,复数及其运算的几何解释在数学中有着重要的地位,在物理学、力学中有着广泛的应用。
在这一讲中我们要比较详细地解释一下复数及其四则运算的几何意义,并且用一些有趣的例子来说明怎样利用复数演算来证平面几何题。
1. 复数的几何意义
大家知道,如果我们在平面上引进一个笛卡儿坐标系,那么任何一个复数
$$z=a+b_{i} \quad (a, b \text { 为实数})$$都可以用平面上坐标为 $(a,b)$ 的点 $P$ 来表示 (图 1)。这样一来,我们就可以在全部复数和平面上的全部点之间建立起一个一一对应的关系:每个复数 $z$ 由一个唯一的点 $P$ 来代表,每个点 $P$ 代表一个唯一的复数 $z$。我们把复数 $z$ 称为点 $P$ 的坐标,并把点 $P$ 直接称为点 $z$
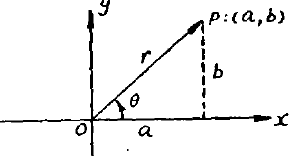 图 1
图 1
横坐标轴上的点代表实数,因此这个坐标轴称为实轴。纵坐标轴上的点代表形为 $bi$ 的纯虚数,因此这个坐标轴称为虚轴。
点 P 在平面上的位置也可以由向径 $\overrightarrow {OP}$ 的长度 $r$ 以及 $\overrightarrow {OP}$ 与实轴正向所成的角 $\theta$ 来决定。$r$ 称为复数 $z$ 的模,$\theta$ 称为 $z$ 的幅角,常用的记号是
$$ r=|z|, \quad \theta=\operatorname {Arg} z. $$如果 $z$ 的模和幅角分别是 $r$ 和 $\theta$,那么它的实部和虚部将是
$$ a=r \cos \theta, \quad b=r \sin \theta, $$因此我们有
$$ z=r (\cos \theta+i \sin \theta). $$复数的这种表示式在下面是很有用的。
注意,当我们诽到 $z$ 的幅角的时候,我们永远把正半实轴从它的原有位置反着时针方向转到向径 $\overrightarrow {OP}$ 的位置时所扫过的那个角当作正的,把顺着时针方向扫过的角当作负的。例如 $i$ 这个点位于虚轴上半,所以它的幅角是 $\pi / 2$, 而 $-i$ 这个点位于虚轴下半,它的幅角为 $-\pi / 2$。
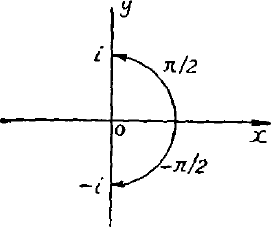 图 2
图 2
一个复数的幅角不是唯一确定的,如果。是 $\theta$ 的幅角,则 $\theta+2 n \pi (n=0,\pm 1, \pm 2, \cdots)$ 也是 $z$ 的幅角。当 $z= 0$ 时,幅角失去意义。
我们知道复数 $z=a+bi$ 的模是
$$ \begin {aligned} r &=|z|=\sqrt {a^{2}+b^{2}}\\ &=\sqrt {(a+b i)(a-b i)}=\\ &=\sqrt {z \overline {z}} \end {aligned} $$所以
$$ z \bar {z}=|z|^{2} $$这里复数
$$\bar {z}=a-bi$$称为 $z$ 的共轭复散。
有趣的是位于以原点为中心,$1$ 为半径的圆周 (单位圆周) 上的复数。此种复数的模为 $1$, 因此它们具有形式
$$ c (\theta)=\cos \theta+i \sin \theta $$我们知道
$$ \begin {aligned} c (\theta_{1}) C (\theta_{2}) =&(\cos \theta_{1}+i \sin \theta_{1})\left (\cos \theta_{2}+i \sin \theta_{2}\right) \\ =&\left\{\left (\cos \theta_{1} \cos \theta_{2}-\sin \theta_{1} \sin \theta_{2}\right)\right.\\ &i\left (\cos \theta_{1} \sin \theta_{2}+\cos \theta_{2} \sin \theta_{1}\right)\} \\ =&\cos \left (\theta_{1}+\theta_{2}\right)+i \sin \left (\theta_{1}+\theta_{2}\right) \\ =&c\left (\theta_{1}+\theta_{2}\right) \end {aligned} $$这就是说,两个模为 $1$ 的篡数相乘时,只要把它们的幅角相加就行了。在这里幅角 $\theta$ 所起的作用相当于幂式 $a^x$ 中指数 $x$ 所起的作用,因此我们采用记号 $e^{i\theta}$ 来代表复数 $C (\theta)$:
$$ e^{i \theta}=\cos \theta+i \sin \theta $$我们有
$$ e^{i \theta_{1}} \cdot e^{i \theta_{2}}=e^{\prime\left (\theta_{1}+\theta_{3}\right)} $$有了这个记号,任意复数 $z$ 可写作
$$ z=r e^{i \theta} $$而它们的共轭复数是
$$ \overline {z}=r e^{-i \theta} $$不过要注意,在这里只是一个纯粹的记号而已。
复数 $z$ 除了可以看作平面上的一个点之外,也可以看作平面上的一个向量:这个向量在实轴和虚轴两个方向上的分量分别是 $a$ 和 $b$,因而它的长度是 $|z|$。在这里向量的起点究竟是哪一点,那是完全无关重要的。因此,平面上任意两个向量,只要它们的长度相等,方向相同,就可以表示同一复数。表示同一复数的有无穷多个向量。由于这些向量大小方向完全相同,我们把它们看作同一向量,此种向量称为自由向量。
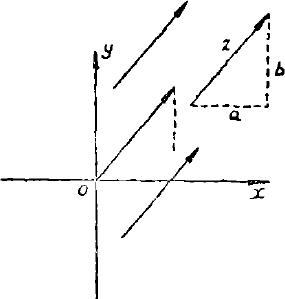 图 3
图 3
如果向量 $z$ 的起点在坐标原点,那么它的终点就是点 $z$。以原点为起点的那个向量称为复数 $z$ 的位置向量。
现在我们来看一看复数的四则运算具有怎样的几何意义。
(一) 复数的加 (减) 法。两个复数
$$ z_{1}=a_{1}+b_{1} i,\quad z_{2}=a_{2}+b_{2}{i} $$相加减时,其实部和虚部分别相加减。这就是说,代表 $z_1,z_2$ 的向量应该按照普通的平行四边形定律相加减。为了将向量 $z_1$ 和 $z_2$ 相加,我们把 $z_2$ 的起点放在 $z_1$ 的终点上,这时由气的起点引向 $z_2$ 的终点的那个向量就是 $z_1 + z_2$(图 4)。
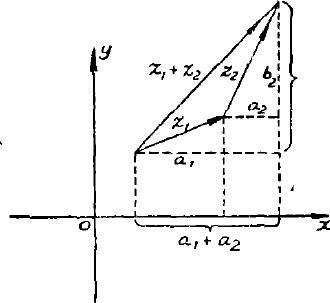 图 4
图 4
我们知道复数的模就是代表它的向量的长度,但在一个三角形中两边长度之和不小于第三边的长度,故从图 4 中立即可得重要不等式
$$ \left|z_{1}+z_{2}\right| \leqslant\left|z_{1}\right|+\left|z_{2}\right|. $$推而广之有
$$ \left|z_{1}+z_{2}+\cdots+z_{n}\right| \leqslant\left|z_{1}\right|+\left|z_{2}\right|+\cdots+\left|z_{n}\right|. $$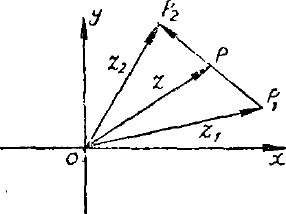 图 5
图 5
从向量相加的规律中,我们还可以看到,如果平面上二点 $P_1$ 和 $P_2$ 的坐标是 $z_1$ 和 $z_2$, 那么向量
$$ \overrightarrow {P_{1} P_{2}}=z_{2}-z_{1} $$现在我如果 $P_1$,$P_2$ 二点的连线上有一点 P, 它满足条件
$$ \frac {\overline {P P}_{2}}{\overline {P_{1} P}}=\lambda / \mu $$这个点 $P$ 的坐标 $z$ 应该怎样求?注意:在这样的情况下,我们说点 $P$ 按比例 $\lambda : \mu$ 分割线段 $P_1P_2$, 如果 $P$ 位于线段 $P_1P_2$ 之内,这个比值正的,否则为负。由于
$$ \overrightarrow {P P_{2}}=z_{2} \rightarrow z, \quad \overrightarrow {P_{1} P}=z-z_{1}, $$所以我们有
$$ \frac {z_{2}-z}{z-z_1}=\lambda / \mu, $$由此即得
$$ z=\frac {\lambda}{\lambda+\mu} z_1+\frac {\mu}{\lambda+\mu} z_{2}. $$如命
$$ \alpha=\frac {\lambda}{\lambda+\mu} $$则有
$$ z=\alpha z_{1}+(1-\alpha) z_{2} $$特别当 $P$ 为线段的中点时,由于 $\lambda=\mu$ 我们有
$$ z=\frac {z_{1}+z_{2}}{2} $$这就是求两点连线的中点公式。
由上面的分析中我们还可以得出下面这样一个重要的结论:
平面上三点 $z_{1}, z_2, z_3$ 共线的充分必要条件是:存在三个不全为零的实数 $l,m,n$, 使得
$$ \left\{\begin {array}{l}{l+m+n=0} \\ {l {z_{1}}+m z_{2}+n z_{3}=0}.\end {array}\right.\tag {*} $$证如果 $z_{1}, z_2, z_3$ 共线,那么 $z_3$ 应按某种比例分割 $z_1,z_2$ 的联线段,即
$$z_{3}=\alpha z_{1}+(1-\alpha) z_{2}.$$命
$$ i=\alpha, m=(1-\alpha), n=-1. $$这就是三个不全为零的实数,并且
$$ \left\{\begin {array}{l}{l+m+n=0} \\ {l {z_{1}}+m z_{2}+n z_{3}=0}.\end {array}\right. $$现在反过来,假设存在三个不全为零的实数使得(*)成立,我们不妨假定其中 $n\neq 0$, 那么就有
$$ \begin {aligned} z_{3} &=\left (-\frac {l}{n}\right) z_{1}+\left (-\frac {m}{n}\right) z_{2} \\ &=\frac {l}{l+m} z_{1}+\frac {m}{l+m} z_{2}. \end {aligned} $$也就是说,$z_3$ 是按比例 $l:m$ 分割 $z_1, z_2$ 的联线段的那个点,这三点当然共线。
(二)复数的乘(除)法现在社我们来看一看复数的乘(除)法有怎样的几何意义。设
$$ z_{1}=r_{1} e^{i \theta_{1}}, \quad z_{2}=r_{2} e^{i \theta_{2}} $$那么我们有
$$ z_{1} z_{2}=r_{1} r_{2} e^{i\left\{\theta_{1}+\theta_{0}\right)}, \quad z_{1} /z_{2}=\frac {r_{1}}{r_{2}} e^{i\left (\theta_{1}-\theta_{3}\right)}\left (r_{2} \neq 0.\right) $$这就是说,两个搜数相乘(除)时,其模相乘(除),其幅角相加(减)。
$$ \begin {aligned}\left|z_{1} \cdot z_{2}\right| &=\left|z_{1}\right|\left|z_{2}\right|, \operatorname {Arg}\left (z_{1} z_{2}\right)=\\ &=\operatorname {Arg} z_{1}+\operatorname {Arg} z_{2} .\end {aligned} $$因此,为了要作出向量 $z_1,z_2$, 只要把向量 $z_1$ 的长度乘上 $r_2$,并且同时把这个向量反着时针方向转动一角度 $\theta_2$ 的就行了。
从这里我们看到如果我们值把某个向量 $z$ 反(顺)着时针方向转动一个角度 $a$ 只要用 $e^{ia}$(或 $e^{ia}$)去乘 $z$ 就行了。特别,如果我们想把向量 $z$ 朝左(右)转一个直角,只要用 $i$(或 $-i$ 去乘 $z$ 就行了。
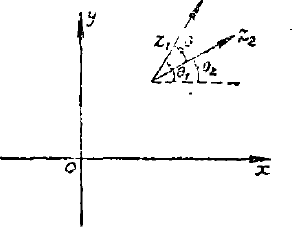 图 6
图 6
此外我们还看到,为了求出向量 $z_1,z_2$ 之间的夹角 $\theta$, 只要作出复数 $z_2/z_1$ 的幅角就行。
2. 几何证题举例
现在我们举出一些例子,说明怎样利用前面所诽的一些简单的槪念来证平面几何为。这里给出的证法都是通过复数的代数演算给出的,因此称为分析证送。大家在平面几何课程中学到过的那种证法称为综合证法。这里我们旣出一个题的分柝证法,也给岀它们的综合证法。
例 1.证明三角形的三条中线相交于一点。
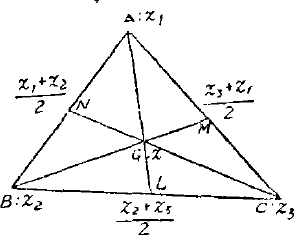 图 7
图 7
证:设三角形的三个顶点 $A,B,C$ 的坐标为 $z_1,z_2,z_3$ 那么它的三个边的中点 $L,M,N$ 的坐标将是
$$\frac {z_{2}+z_{3}}{2},\frac {z_{3}+z_{1}}{2},\frac {z_{1}+z_{2}}{2}.$$考虑中线 $AL$ 和 $CN$。设它们的交点 $G$ 的坐标为 $z$,由于 $C,G,N$ 共线,故应有
$$ z=\alpha\left (\frac {z_{1}+z_{2}}{2}\right)+(1-a) z_{3}.\tag {1} $$由于 $A,G,L$ 共线,故应有
$$ z=\beta\left (\frac {z_{2}+z_{3}}{2}\right)+(1-\beta) z_{1}.\tag {2} $$由此即得
$$ \begin {aligned} &\alpha\left (\frac {z_{1}+z_{2}}{2}\right)+(1-a) z_{3}\\ &=\beta\left (\frac {z_{2}+z_{3}}{2}\right)+(1-\beta) z_{1}, \end {aligned} $$整理之得
$$ (\alpha-2+2 \beta) z_{1}+(\alpha-\beta) z_2+\\ +(2-2 \alpha-\beta) z_{3}=0, $$ 并且 $$(a-2+2 \beta)+(a-\beta)+(2-2 \alpha-\beta)=0.$$但 $z_1,z_2,z_3$ 不共线,故根据前面所证结论应有
$$ \left\{\begin {array}{l}{\alpha-2+2 \beta=0} \\ {\alpha-\beta=y} \\ {2-2 \alpha-\beta=0}.\end {array}\right. $$由此即得
$$ \alpha = \beta=2 / 3 $$以 $\alpha = 2/3$ 代入式(1),就得
$$ z=\frac {z_{1}+z_{2}+z_{3}}{3} $$因此,我们看到三角形的任意两条中线都交于 $z=\frac {1}{3}(z_{1}+z_{2}+z_{3})$ 这一点,即三条中线共点。
这题的综合证法是大家都知道的,不在此处讲了,我们只指出分析方法给出了三角形重心的坐标。
例 2.从前有一个海盗,把他抢来的宝物埋藏在一个海岛上,并在自己的日记本上写了如下的记录:“XX 年 X 月 X 日,我从海岛岸边一棵松树 $P$ 处登陆,向左前方走了一段路,遇到一块大石头 $A$ 在这里我朝左转了 $90^{\circ}$ 再走了同样长的一段路,达到海岛上一点 $A'$。后来我又从松树处出发,向右前方走了一段路,遇到一块大石头 $B$,在这里我朝右转了 $90^{\circ}$ 再走了同样长的一段路,达到一点 $B'$。我把宝物埋在 $A',B'$ 二点连线的中点上。”
过了若干年之后,他的后人发现了这本日记,来到了这个海岛上。他发现两块石头仍然存在,可是岸旁那棵松树已经不存在了。请问这位海盗的后人有没有办法把埋藏的宝物重新找出来?
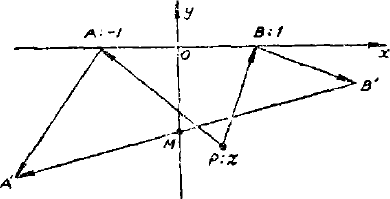 图 8
图 8
分析解法。我们以 $A,B$ 二点的联线 $l$ 作为实袖,以二点联线的中点 $O$ 为原点引进一个坐标系。不妨设
在这个坐标系中 $A$ 的坐标是 $-1$, $B$ 的坐标是 $1$,设点 $Р$ 的坐标为 $z$ 那么向量
$$ \overrightarrow {P A}=-1-z, \overrightarrow {P B}=1-z $$向量 $\overrightarrow {AA'}$ 可由向量 $\overrightarrow {PB}$ 反着时针方向转 $\frac {\pi}{2}$ 得到,故
$$ \overrightarrow {d A'}=-i (1+z) $$但这个向量的起点 $A$ 的坐标为 $-1$, 故其终点 $A'$ 的坐标为
$$-1-i (1+z). $$同理,向量 \(\overrightarrow {B B'}\) 由向量 $\overrightarrow {P B}$ 顺着时针方向转 $\frac {\pi}{2}$ 得到,故
$$ \overline {B B^{\prime}}=-i (1-z). $$从而知 $B'$ 的坐标为
$$1-i (1-z).$$$A',B'$ 联线段中点 $M$ 的坐标应是
$$ \frac {1}{2}\{[-1-i (1+z)]+[1-i (1-z)]\}=-i. $$这就是说,不论 $P$ 的坐标为何,宝物埋藏点 $M$ 总是点 $-i$, 即以 $AB$ 为底的等腰直角三角形的顶点。
如果点 $P$ 在 $l$ 的另一侧,则 $M$ 的坐标是 $i$,因此后来的人只要以 $AB$ 为底作一正方形,那么宝物一定埋在正方形的另外两个顶点上。
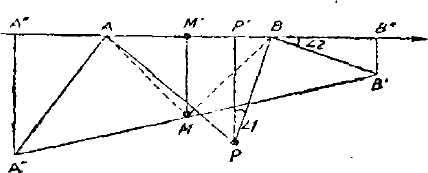 图 9
图 9
综合解法 设 $A'$,$B'$ 二点联线段的中点为 $М$, 作 $PP'$,$A^{\prime} A^{\prime \prime}, B^{\prime} B^{\prime \prime}, M A^{\prime}$ 垂直于 $A,B$ 二点的联线 $l$ 由于 $M$ 是梯形 $A^{\prime} A^{\prime \prime} B^{\prime \prime} B^{\prime}$ 一个腰的 $A'$ 中点,故 $M'$ 必是另一腰 $A"B"$ 的中点。另一方面,在直角三角形 $\triangle P P^{\prime} B$ 和 $\triangle B B^{\prime \prime} E^{\prime}$ 中,由于 $\overline {PB}=\overline {BB}$,$\angle 1=\angle 2$,故
$$ \triangle P^{\prime} B \cong \triangle B B^{\prime \prime} B^{\prime} $$因此我们有
$$ \overline {B B^{\prime \prime}}=\overline {P P'} \text {和} \overline {P^{\prime} B}=\overline {B^{\prime} B^{\prime \prime}}. $$同理可知
$$ \overline {A A^{\prime \prime}}=\overline {P P'} \text {和} \overline {P^{\prime} A}=\overline {A^{\prime} A^{\prime \prime}}. $$由于 $M'$ 是 $A"B"$ 的中点,而 $\overline {A A^{\prime \prime}}=\overline {B B^{\prime \prime}}\left (=P P^{\prime}\right)$, 故 $M'$ 必定同时也是 $AB$ 的中点。另一方面,我们有
$$ \overline {M M^{\prime}}=\frac {\overline {A^{\prime} A^{\prime \prime}}+\overline {B^{\prime} B^{\prime \prime}}}{2}=\frac {\overline {P^{\prime} A}+\overline {P^{\prime} B}}{2}=\frac {\overline {A B}}{2}, $$故有
$$\overline {M M^{\prime}}=\overline {M^{\prime} A}=\overline {M^{\prime} B}$$即 $\triangle M M^{\prime} A, \triangle M M^{\prime} B$ 为等腰直角三角形,因而 $\triangle AMB$ 是等腰直角三角形。由此可知宝物埋藏点是以 $AB$ 为底的等腰直角三角形的顶点。
例 3. 以平行四边形 $▱ABCD$ 的每个边为边,向四边形之外作一正方形。证明这四个正方形的四个中心依次联结起来是一正方形。
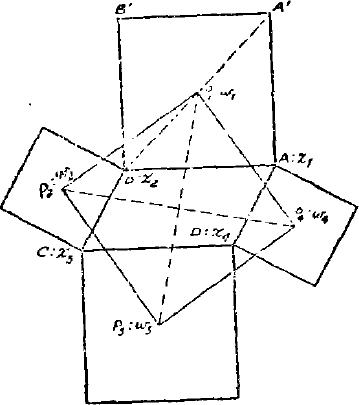 图 10
图 10
分析证法 命平行四边形的四个顶点 $A,B,C,D$ 的坐标为 $z_{1}, z_{2}, z_{3}, z_{4}$。首先注意
$$ \overrightarrow {A B}=z_{2}-z_{1}, \overrightarrow {D C}=z_{3}-z_{4} $$但这两个向量方向相同,长度相等,故必有
$$ z_{2}-z_{1}=z_{3}-z_{4} $$或
$$ z_{1}+z_{3}=z_{2}+z_{4} $$现在注意向量 $\overrightarrow {A A^{\prime}}$ 是由向量 $\overrightarrow {A B}=z_{2}-z_{1}$ 顺着时针方向转 $\frac {\pi}{2}$ 得到的,故
$$ \overrightarrow {A A^{\prime}}=-i\left (z_{2}-z_{1}\right), $$但达个向量的起点为 $z_1$,故其终点为
$$-i (z_{2}+x_{1})+z_{1}. $$正方形 $A A^{\prime} B B$ 的中心是对角线 $A^{\prime} B$ 的中点,故其坐标为
$$ \begin {aligned} P_{1} : w_{1} &=\frac {1}{2}\left\{\left [-i\left (z_{2}-z_{1}\right)+z_{1}\right]+z_{2}\right\}\\ &=\frac {1}{2}\left\{(1+i) z_{1}+(1+t) z_{3}\right\} .\end {aligned} $$同理可知,其他三个正方形的中心是
$$ \begin {aligned} P_{2} : w_{2}&=\frac {1}{2}\left\{(1+i) z_{2}+(1+i) z_{3}\right\}\\ P_{3} : w_{3}&=\frac {1}{2}\left\{(1+i) z_{3}+(1+z) z_{4}\right\} \\ P_{4} : w_{4}&=\frac {1}{2}\left\{(1+i) z_{4}+(1+i) z_{1}\right\}. \end {aligned} $$利用前面的条件
$$ x_{1}+z_{3}=z_{2}+z_{4} $$立即可以算岀
$$ \begin {aligned} \frac {1}{2} \left (w_{1}+u_{3}\right)&=\frac {1}{2}\left (w_{2}+w_{4}\right)\\ &=\frac {1}{4}\left (z_{1}+z_{2}+z_{3}+z_{4}\right) .\end {aligned} $$这就是说,线段 $P_1P_3$ 和 $P_2P_4$ 有相同的中点。也就是说,四边形 $P_{1} P_{2} P_{3} P_{4}$ 的对角线相互等分。
其次,我们有
$$ \begin {aligned} w_{2}-w_{4}=&\frac {1}{2}\{(1+t)(z_{2}-z_{4})\\ &+(1-t)(z_{3}-z_{1}) \},\\ w_{1}-u_{3}=&\frac {1}{2}\{(1+t)(z_{1}-z_{2}) \\ &+(1-t)(z_{2}-z_{4}) \}. \end {aligned} $$因此
$$ \begin {aligned} (w_{1}-w_{3})&=(w_{2}-w_{4}) \\ |w_{1}-w_{3}|&=|w_{2}-w_{3}| \end {aligned} $$这就是说 $P_1P_3$ 和 $P_2P_4$ 相互垂直,而且长度相等。因此 $P_{1} P_{2} P_{3} P_{4}$ 是一个正方形。
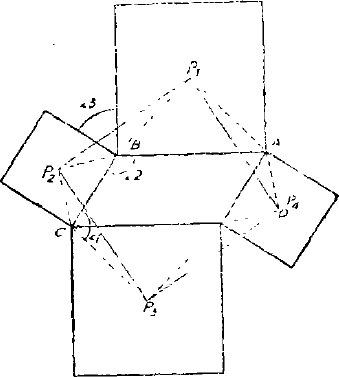 图 11
图 11
综合解法 考虑三角形 $\triangle P_{1} B P_{2}$ 和 $\triangle P_{3} C P_{2}$。我们知道
$$ \overline {P_{1} B}=\overline {P_{3} C}=\left (\frac {\overline {A B}}{\sqrt {2}}\right), $$ $$ \overline {P_{2} B}=\overline {P}_{2} C=\left (\frac {\overline {B C}}{\sqrt {2}}\right). $$另一方面,我们知道
$$ \begin {aligned} \angle 3 &=\pi-\angle 2 \\ &=\pi-(\pi-\angle 1) \\ &=\angle 1 \end {aligned} $$故
$$ \angle P_{1} B P_{2}=\angle P_{3} C P_{2}=\left (\frac {\pi}{3}+\angle 1\right), $$因此
$$ \triangle P_{1} BP_{2} \cong \triangle P_{3} C P_{2} $$从而得
$$ \overline {P_{1} P_{2}}=\overline {P_{2} P_{3}} $$同理可知
$$ \overline {P_{1} P}=\overline {P_{2} P_{3}}=\overline {P_{3} P}_{4}=\overline {P_{4} P}_{1}. $$其次
$$ \angle P_{1} P_{2} B=\angle P_{3} P_{2} C, $$因此
$$ \begin {aligned} \angle P_{1} P_{2} P_{3} &=\angle B P_{2} C+\angle P_{1} P_{2} B-\angle P_{3} P_{2} C \\ &=\angle B P_{2} C=\frac {\pi}{2}. \end {aligned} $$同理可知
$$ \angle P_{1} P_{2} P_{3}=\angle P_{2} P_{3} P_{4}=\angle P_{3} P_{4} P_{1}=\angle P_{4} P_{1} P_{2}=\frac {\pi}{2}, $$故 $P_{1} P_{2} P_{3} P_{4}$ 为正方形。
例 4. 平面上有一个固定的圆周 $K$。圆外有一固定点 $A$, 圆周上审一动点 $B$,对 $B$ 的每一个位置我们以 $AB$ 为底作一正三角形 $△ABC$
我们问:当 $B$ 在圆周 $К$ 上运动时,正三角形 $ABC$ 的第三个顶点 $C$ 将会描出怎样的轨迹?
注意,以 $AB$ 为底可以作出两个正三角形来。我们只考虑其中那样一个正三角形,当我们从 $А$ 向 $B$ 时,这个正三角形出现在我们的右手边。
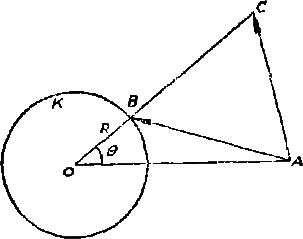 图 12
图 12
分析解法 我们以 $К$ 的中心为原点,$OA$ 联线为实轴引入一坐标系。设 $A$ 在这坐标系中的坐标为 $a$
如果 $K$ 的半径为 $R$,则 $B$ 的坐标将是 $R e^{i \theta}$。现在注意向量 $\overrightarrow {A B}=R e^{i \theta}-a$,向量 $\overrightarrow {A C}$ 是由向 \(\overrightarrow {A B}\)
顺着时针方向转 $\frac {\pi}{3}$ 得到的,所以
$$ \overrightarrow {A C}=e^{-\frac {\pi}{3}-i}\left (R e^{i \theta}-a\right) $$但 $\overrightarrow {A C}$ 的起点为 $a$,故 $C$ 的坐标应是
$z=e^{-\frac {\pi}{3} i}\left (R e^{i \theta}-a\right)+a.$从而
$$ z-a\left (1-e^{-\frac {\pi}{3} i}\right)=R e^{i\left (\theta-\frac {x}{3}\right)} $$两边取模得
$$ \left|z-a\left (1-e^{-\frac {\pi}{3} i}\right)\right|=R. $$这就是说,$C$ 到 $a\left (1-e^{-\frac {\pi}{3} i}\right)$ 这个点的距离永远是 $R$ 因此 $C$ 的轨迹是以 $a\left (1-e^{-\frac {\pi}{3} i}\right)$ 为中心,$R$ 为半径的圆周。
现在让我们看轨迹的圆心究竟在哪里。我们知道
$$ e^{-\frac {\pi}{3} i}=\frac {1-i \sqrt {3}}{2}, $$因此
$$ 1-e^{-\frac {\pi}{3} i}=\frac {1+t \sqrt {3}}{2}=e^{i \frac {\pi}{3}}, $$ $$ a\left (1-e^{-\frac {\pi}{3}-i}\right)=a e^{i \frac {\pi}{3}}. $$这就是说,轨迹的圆心是将向量 $\overrightarrow {O A}$ 反着时针方向转 $\frac {\pi}{3}$ 得到的向量 $\overrightarrow {O A_1}$ 的终点。因此,我们所要求的轨迹可以下法作出:以 $OA$ 为底作一正三角形,以这个正三角形的第三个顶点为中心 $R$ 为半径作一圆,此圆即所要求的轨迹。
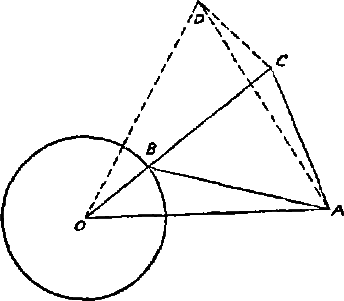 图 13
图 13
综合解法以 $OA$ 为底作正三角形 $\triangle O A D$。考虑三角形 $\triangle BAO$ 和 $\triangle CAD$。我们有
$$ \overline {B A}=\overline {C A},\quad \overline {O A}=\overline {D A}. $$另一方面,
$$ \angle C A D=\frac {\pi}{3}-\angle B A D, $$ $$ \angle B A O=\frac {\pi}{3}-\angle B 4 D, $$因此
$$ \angle CA D=\angle BA O. $$从而得
$$ \triangle B A O \cong \triangle C A D. $$故
$$ \overline {D C}=\overline {O B}=R. $$因此 $C$ 位于以 $D$ 为中心为半径的圆周之上。
例 5 . 设 $\triangle A B C$ 为任意三角形,以这个三角形的每个边为底,向外部作—正三角形。证明这三个正三角形的重心是另一正三角形的三个顶点。
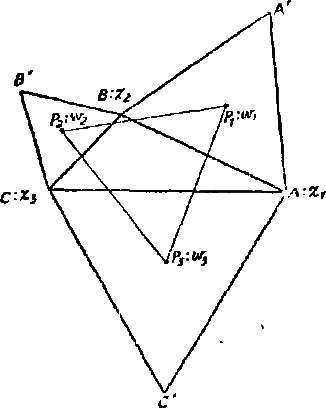 图 14
图 14
证设三角形 $\triangle A B C$ 三个顶点的坐标为 $z_1,z_2,z_3$。向量 $\overrightarrow {A A^{\prime}}$ 是由向量 $\overrightarrow {A B}$ 顺着时针方向转 $\frac {\pi}{3}$ 得到的,因此,如果记 $\xi=e^{-\frac {\pi}{3} i}$, 则有
$$ \overrightarrow {A A^{\prime}}=\xi\left (z_{2}-z_{1}\right) $$但 $A$ 的坐标为 $z_1$,故 $A'$ 的坐标为
$$ \xi\left (z_{2}-z_{1}\right)+z_{1}=\xi_{z_{2}}+(1-\xi) z_{1}. $$三角形 $\triangle A A^{\prime} B$ 的重心 $P_1$>的坐标是
$$\begin {aligned} P_{1} : w_{1} &=\frac {1}{3}\left\{z_{1}+z_{2}+\xi_{z_{2}}+(1-\xi) z_{1}\right\} \\ &=\frac {1}{3}\left\{(2-\xi) z_{1}+(1+\xi) z_{2}\right\} \end {aligned}.$$同理,其余两个三角形的重心是
$$ \begin {aligned} P_{2} : w_{2} &=\frac {1}{3}\left\{(2-\xi) z_{2}+(1+\xi)_{z_{3}}\right\}, \\ P_{3} : w_{3} &=\frac {1}{3}\left\{(2-\xi) z_{3}+(1+\xi)_{z_{1}}\right\}. \end {aligned} $$这样一来,便有
$$ \begin {aligned} 3\left (w_{2}-w_{1}\right)=&(\xi-2) z_{1}+(1-2 \xi) z_{2}+\\ &+(1+\xi) z_{3} ,\end {aligned} $$ $$ \begin {aligned} 3\left (w_{3}-w_{2}\right)=&(\xi-2) z_{2}+(1-2 \xi) z_{3}+\\ &+(1+\xi) z_{1}, \end {aligned} $$ $$ \begin {aligned} 3\left (w_{1}-w_{3}\right)=&(\xi-2) z_{3}+(1-2 \xi) z_{1}+\\ &+(1+\xi) z_{2}. \end {aligned} $$但
$$ \xi^{3}=e^{-n i}=-1, $$ $$ \xi^{2}=e^{-\frac {2 \pi i}{3}}=\frac {-1-\sqrt {3}}{2}=\xi-1, $$故有
$$ \begin {aligned} {\xi^{2}\left (w_{3}-w_{2}\right)=u_{2}-w_{1}} \\ {\xi^{2}\left (a_{1}-u_{3}\right)=w_{3}-u_{2}} \end {aligned} $$两边取模,并注意 $|\xi|=1$,得 $$ |w_{3}-w_{2}|=| w_{2}-w_{1}|=| w_{3}-w_{1} | $$
$\triangle P_{1} P_{2} P_{3}$ 为一正三角形。
3. 一个有趣约数学竞赛题
以上举的四个例子,除了第 1 例之外,大致上属于同一类型,并且技巧性也不是太强的,下面这个题是一个外国数学竟赛题,我们也用分析方法来解它,由于这题较难所以技巧性也较强。题目是这样说的:
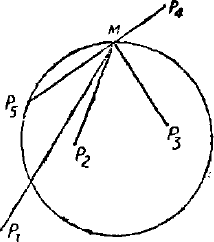 图 15
图 15
在平面上给定了一个半径为 1 的圆和另外某 $n$ 个点(可以在圆内,圆外,也可以在圆周上)$P_{1}, P_{2}, \cdots, P_{n}$。证明在圆周上一定可以找到一个点 $M$ 使得
$$ \overline {M P_{1}} \cdot \overline {M P}_{2} \cdots \overline {M P_{n}} \geq 1 $$为了证明这一事实,我们先证明一个公式。设 $\xi=e^{\frac {2 \pi i}{N}}$($N$ 为自然数) 。
那么对任意整数 $0< d< N$ 来说
$$ 1+\xi^{d}+\xi^{2 d}+\cdots \cdots+\xi^{(N-1) d}=0 $$事实上,如果 $0< d< N$ 则
$$ \xi^{d}=e^{\frac {2 \cdot d \pi}{N} i} \neq 1, $$ 但 $$ \left (\xi^{d}\right)^{N}=e^{2 d_{\pi i}}=1, $$故有
$$ \begin {aligned}\left (\xi^{d}\right)^{N}-1 &=\left (\xi^{d}-1\right)(\xi^{(N-1) d}+\cdots+\\ &+\xi^{2 d}+\xi^{d}+1 )=0 \end {aligned} $$即
$$ 1+\xi^{d}+\xi^{2 d}+\cdots+\xi^{(N-1) d}=0. $$现在我们在平面上以所给圆的圆心为原点引入一个坐标系,设 $P_{1}, P_{2}, \cdots, P_{n}$ 的坐标为 $z_{1}, z_{2}, \dots, z_{n}$ 命圆周上一点 $M$ 的坐标为 $z$,那么
$$ \begin {aligned} P &=\overline {M P_{1}} \cdot \overline {M P}_{2} \cdots \overline {M_{n}}=\\ &=\left|z-z_{1}\right| \cdot\left|z-z_{2}\right| \cdots\left|z-z_{n}\right| \end {aligned} $$由于当 $z$ 在单位圆周上时 $|z| = 1$, 故上式又可写成
$$ \begin {aligned} P &=|z|\left|z-z_{1}\right|\left|z-z_{2}\right| \cdots\left|z-z_{\mathfrak {a}}\right| \\ &=| z\left (z-z_{1}\right)\left (z-z_{2}\right) \cdots\left (z-z_{\mathfrak {a}}\right) \} \\ &=|f (z)|, \end {aligned} $$其中,
$$ \begin {aligned} f (z)&=z\left (z-z_{1}\right)\left (z-z_{2}\right) \cdots\left (z-z_{n}\right)\\ &=z^{n+1}+a_{1} z^{n}+a_{2} e^{n-2}+\cdots+a_{n} z \end {aligned} $$我们的任务是要证明在单位圆周上能找到一点 $z$ 使得
$$ |f (x)| \geq 1. $$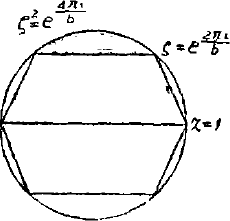 图 16
图 16
为此目的,我们作一个内接于单位圆的正 $n+1$ 边形,使得它的一个顶点为 $1$。如命
$$ \xi=e^{\frac {2\pi i}{n+1}} $$则这个正 $n+1$ 边形的顶点将是
$$ 1, \xi, \xi^{2}, \cdots, \xi^{n}. $$我们证明这 $n+1$ 个点中必有一个点 $\xi^k$,它满足条件
$$ \left|f\left (\xi^{k}\right)\right| \geq 1. $$不然的话,我们将有
$$ |f (1)|< 1,|f (\xi)|< 1, \cdots ,|f (\xi^n)|< 1 $$可是
$$ \begin {aligned} f (1)=& 1+a_{1} \cdot 1+a_{2} \cdot 1+\cdots+\\ &+a_{k} \cdot 1+\cdots+ a_ n, \end {aligned} $$ $$ \begin {aligned} f (\xi)&=1+a_{1} \xi^{n}+a_{2} \xi^{n-1}+\cdots+\\ &+a_{k} \xi^{k}+\cdots+a_{n}\xi, \end {aligned} $$ $$ \begin {aligned} f (\xi^2)&=1+a_{1} \xi^{2 n}+a_{2} \xi^{2 (n-1)}+\cdots+\\ &+a_{k} \xi^{2k}+\cdots+a_{n}\xi^2, \end {aligned} $$ $$\cdots\cdots\cdots\cdots\cdots,$$ $$ \begin {aligned} f (\xi^2)&=1+a_{1} \xi^{n n}+a_{2} \xi^{n (n-1)}+\cdots+\\ &+a_{k} \xi^{nk}+\cdots+a_{n}\xi^n \end {aligned} $$两边相加,并注意
$$ 1+\xi^{k}+\xi^{2 s}+\cdots+\xi^{n k}=0,1 \leq k \leq n, $$ 得 $$ n+=f (1)+/(\xi)+f\left (\xi^{2}\right)+\cdots+f\left (\xi^{n}\right) $$两边取模,并利用前面提到过的不等式
$$ \begin {aligned} n+1&=|f (1)+/(\xi)+f\left (\xi^{2}\right)+\cdots+f\left (\xi^{n}\right)|\\ &\leq |f (1)|+|f (\xi)|+\left|f\left (\xi^{2}\right)\right|+\cdots+ |f (\xi^n)|\\ &< 1+1+1+\cdots+1\\ &=n+1. \end {aligned} $$这就得出了矛盾。这个矛盾说明,必有一个 $k$ 使得
$$|f (\xi^{k})| \geq 1.$$由这个题的解法中我们轻可以得出下面这样一个有趣的定理,这个定理在高等数学中有很重要的推广。
定理如果多项式
$$ P (z)=a_{m} z^{m}+a_{m-1} z^{m-1}+\cdots+a_{0} $$的次数 $m< n$ 则 $P (z)$ 打在任意圆内接正 $n$ 边形的各个顶点的值的平均等于它在圆心的值。
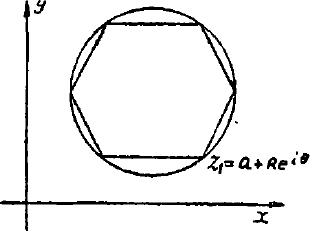 图 17
图 17
证设圆形为 $a$ 圆的半径为 $R$。首先我们证明,多项式 $Р(z)$ 可改写成
$$ P (x)=a_{m}(z-a)^{m}+b_{m-1}(z-a)^{m-1}+\cdots+b_0\tag {i} $$的形式。这一点可用数学归纳法来证。
当 $n= 0$ 时,这是显然的。如果对次数不大于 $k$ 的多项式这一事实成立,那么对任意 $k+1$ 次多项式
$$ P (z)=a_{k+1} z^{k+1}+a_{k^{z}} z+\cdots+a_{0} $$我们有
$$ P (z)-a_{k+1}(z-a)^{k+1}=Q (z) $$其中 $Q (z)$ 为次数不大于 $k$ 的多项式。根据归纳假设
$$ Q (z)=b_{k}(z-a)^{k}+\cdots+b_{0} $$因此
$$ \begin {aligned} P (z)=&a_{k+1}(z-a)^{k+1}+b_{k}(z-a)^{k}\\ &+\cdots+b_{0} \end {aligned} $$这就证明了我们的断言。注意当 $P (z)$ 写成 (i) 那种形式时,它在圆心的值是
$$ P (a)=b_{0} $$现在假设圆内接正 $n$ 边形的一个顶点为
$$ z_{1} = a+R e^{i \theta} $$那么它的全部顶点将是
$$ \begin {aligned} z_{1}&=a+R e^{i \theta}, \\ z_{2}&=a+R e^{i (\theta+\frac {2 \pi}{n})}, \\ &\dots,\\ z_{n}&=a+R e^{i (\theta+\frac {2 (n-1) \pi}{n})} \end {aligned} $$为了求得 $P (z)$ 在这 $n$ 个点上的值的平均,只要分别求出 (i) 中每项在这 $n$ 个点上的值的平均就行了。注意当 1$\leq k \leq m$ 时,$k$ 次项 $a_{k}(x-a)^{k}$ 的平均值是
$$ \begin {aligned} M_{k}&= \frac {a_{k}}{n}[(z_{1}-a)^{k}+(w_{2}-a)^{k}+\cdots+(z_{n}-a)^{k} ]\\ &=\frac {a_{k} R}{n}[1+e^{\frac {2 k \pi}{n} i}+c^{\frac {4 k \pi i}{n}}+\cdots+e^{\frac {(2n-1) k \pi}{n} i} ] e^{i k \theta}\\ &=0 \end {aligned} $$而零次项 $b_0$ 的平均值仍是 $b_0$, 故有
$$ \frac {P\left (z_{1}\right)+P\left (z_{2}\right)+\cdots+P\left (z_{n}\right)}{n}=b_{0}=P (a). $$| 作者: | 曾肯成,数学家,密码学家。 |
| 来源: | 《数学通报》1963 年 12 期 |




