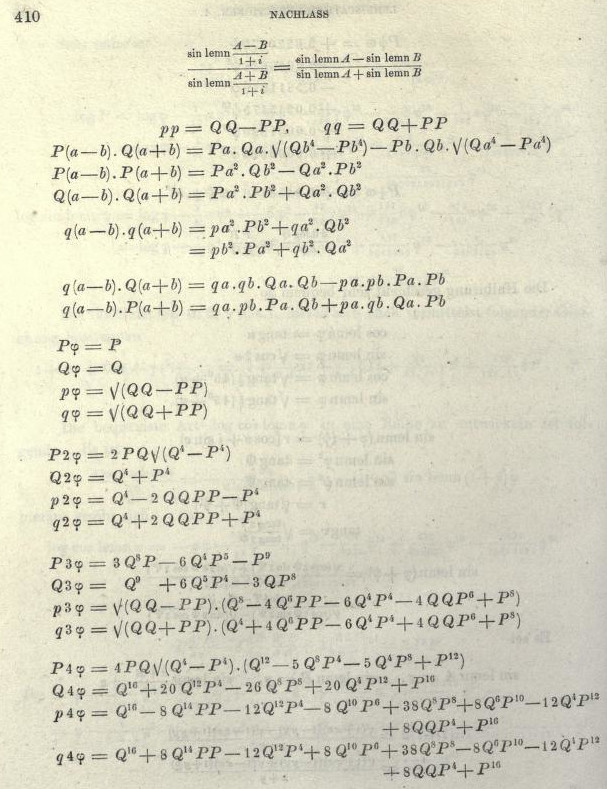
[注：题图是 Gauss 全集第三卷中关于椭圆函数的公式列表。]

1797 年 3 月 Gauss 日记中的某条记录是这样的 [原文无日期，这条记录夹在 3 月 19 日和 21 日的记录之间]：

A potestatibus integr [alis] $\int_{0}^{1}\frac {\mathrm {d} x}{\sqrt {1-x^4}}$ pendet $\sum\left (\frac {m^2+6mn+n^2}{(m^2+n^2)^4}\right)^k$ .关于积分 $\int_{0}^{1}\frac {\mathrm {d} x}{\sqrt {1-x^4}}$ 的幂依赖于 [级数] $\sum\left (\frac {m^2+6mn+n^2}{(m^2+n^2)^4}\right)^k$ 。

Gauss 这本日记本来就可以看做个人的备忘录，如果单独看 Gauss 日记，根本无法看懂他在说什么。幸好同一时期有 Gauss 的 Leiste 算术书上的记录，而这些与日记同一时期出现的公式可以帮助我们理解 Gauss 进一步的思路。

熟悉 Euler 对Basel 问题最初解法的人都知道，Euler 是把多项式的因式分解强行套在整函数 $\sin z$ 上 [注意 $\sin z$ 的零点都是单零点]：

$$\sin z=z\prod_{n=1}^{\infty}(1-\frac {z^2}{\pi^2n^2})$$

我们当然也有

$$\cos z=\prod_{n=1}^{\infty}(1-\frac {z^2}{\pi^2 (n-1/2)^2})$$

Gauss 很显然把同样的方法套在我们上篇提到的函数 $s (u)$ 与 $c (u)$ 上。以 $s (u)$ 为例，我们有

$$\begin {align} s (u)&=\frac {M (u)}{N (u)},\\M (u)&=u\prod_{m,n\geq 0}{}^{'}\left (1-\left (\frac {u}{(m+in)\varpi}\right)^4\right),\\N (u)&=\prod_{m,n\geq 0,\\m,n \,odd}{}^{'}\left (1-\left (\frac {u}{(m+in)\varpi/2}\right)^4\right),\end {align}$$

这里 $\prod {}^{'}$ 表示二重乘积中不取 $m=n=0.$ Gauss 紧接着写下两个等式 [Gauss 全集第十卷第一册，153 页]

$$\begin {align} M (u)&=u\left (1-\frac {1}{60} u^4-\frac {1}{10080} u^8+\cdots\right),\\N (u)&=1+\frac {1}{12} u^4-\frac {1}{10080} u^8+\cdots\end {align}$$

Gauss 到底是怎么得到这个展开式的呢？按高木贞治的《近世数学史谈》第六章的叙述，似乎并没人知道 Gauss 是怎么得到这个展开式的。但我们可以根据 L. Schlesinger 和 A. I. Markushevich 的引用 [这些引用最早都应当来自 Robert Fricke 的工作]，找到 Gauss 全集中的内容来推测一下 Gauss 的思路 (当然不能保证这就是 Gauss 的全部思路)。

Gauss 全集的第八卷 96 页有 Gauss 1799 年的演算。这个演算关于双纽线的特例是这样的：

令 $y=\log s (u)$ . 首先我们有 $\frac {\mathrm {d} s}{\mathrm {d} u}=\sqrt {1-s^4}$ 。那么我们有

$s\frac {\mathrm {d} y}{\mathrm {d} u}=\sqrt {1-s^4}$ 。在这个式子两边继续对 u 微分，整理后我们有

$$\frac {\mathrm {d}^2y}{\mathrm {d} u^2}=-s^2-\frac {1}{s^2}.$$

[从这里开始是作者的推理] 如果 $s (u)=\frac {M (u)}{N (u)},$ 那么 $\frac {\mathrm {d}^2\log M}{\mathrm {d} u^2}$ 的所有极点与 $-\frac {1}{s^2}$ 重合，而 $\frac {\mathrm {d}^2\log N}{\mathrm {d} u^2}$ 的所有极点与 $s^2$ 重合 [为什么？]。进一步， $\frac {\mathrm {d}^2\log M}{\mathrm {d} u^2}+\frac {1}{s^2}$ (或 $\frac {\mathrm {d}^2\log N}{\mathrm {d} u^2}-s^2$ ) 是有界的。然而

$$\frac {\mathrm {d}^2\log M}{\mathrm {d} u^2}=-\sum_{m,n}\frac {1}{(u-(m+in)\varpi)^2}$$

从形式上看来，它是一个双周期 [半纯] 函数 [周期为 $\varpi,i\varpi$ , 与 $s (u)^2$ 相同]，而双周期的有界解析函数必定是常数。考察函数在 $u=0$ 处的性态，我们可以断言， $\frac {\mathrm {d}^2\log M}{\mathrm {d} u^2}=-\frac {1}{s^2}$ (以及 $\frac {\mathrm {d}^2\log N}{\mathrm {d} u^2}=s^2$ )。根据我们上篇中 Lagrange 对反函数的展开式，我们可以得到

$$\begin {align} s (u)^2&=u^2-\frac {1}{5} u^6+\frac {2}{75} u^{10}-\frac {1}{13\cdot25} u^{14}+\cdots,\\ \frac {1}{s (u)^2}&=\frac {1}{u^2}+\frac {1}{5} u^2+\frac {1}{75} u^6+\frac {2}{13\cdot15\cdot25} u^{10}+\cdots\end {align}$$

再根据指数函数的级数展开，我们就可以得到 Gauss 写在 Leiste 算术书中 $M (u),N (u)$ 的级数展开了。[推理到此结束]

[注：Gauss 的时代并不存在完整的复变函数理论，就更不用提 Liouville 定理了。我们不清楚 Gauss 能不能证明 Liouville 定理或其类似物，但是 Gauss 本人应当尝试用数值计算打消自己的疑虑。Gauss 在 Leiste 笔记上曾经将 Stirling 算出的常数 $\varpi/2=1.31102877\cdots$ 代入 $M,N$ 的级数，如果推理正确的话， $M (\varpi/2)=N (\varpi/2)$ 。Gauss 对这个结果进行过两遍计算 (见 Gauss 全集第十卷第一册，154 页及 157 页，前者错误而后者正确)，代入级数前四项进行计算，数值上得出 $|M (\varpi/2)-N (\varpi/2)|<10^{-7},N (\varpi/2)\approx 1.2453445$ 。]

[补注：Gauss 也有可能直接用部分分式分解来断定 $-\frac {1}{s^2}=-\sum_{m,n}\frac {1}{(u-(m+in)\varpi)^2}$ ]

高木贞治在《近世数学史谈》中有如下评论 [第六章，34 页]：

あの時代には収斂の理論は出来ていなかったけれども、発散から生ずる危険はよく知られていたのであって、有能の数学者は不収斂から生ずる誤りに陥っていることは稀有である。特にガウスは幼時から無限級数や無限積の取扱いには数字的計算に由って習熟していたのであるから、収斂などは「勘」で分ったのではなかろうか。那个时代 [指 Gauss 生活的年代][级数以及无穷乘积的] 收敛的理论尚未成型，但人们已经很清楚 [级数及无穷乘积] 发散所带来的危险，有能力的数学家很少会掉进因不收敛而产生的陷阱当中去。Gauss 在年纪还小的时候就对无穷级数和无穷乘积的数值处理十分熟练，因此一定对收敛有着直觉上的感受。

Gauss 所定义的二重积 $M (u),N (u)$ 恰好是绝对收敛的 [为什么？]，因此两个函数都是整函数。但是如果我们把 $M (u)$ 的二重积写成这样 $M (u)=u\prod_{m,n\in \mathbb {Z}}{}^{'}\left (1-\frac {u}{(m+in)\varpi}\right)$ ，二重积就不再绝对收敛，随意交换级数中的项可能会改变函数的性态。后世至少有两种处理方法：

• (Weierstrass) 这是绝大多数人所熟悉的方法。对于 Gauss 的函数 $M (u)$ ,Weierstrass 的改造为 $\sigma (u)=u\prod_{m,n\in \mathbb {Z}}{}^{'}\left (1-\frac {u}{(m+in)\varpi}\right)\exp\left (\frac {u}{(m+in)\varpi}+\frac {u^2}{2 ((m+in)\varpi)^2}\right)$ 这个二重积是绝对收敛的。对其对数求二阶导数，我们得到绝对收敛的二重级数 $-\frac {1}{u^2}-\sum_{m,n\in\mathbb {Z}}{}^{'}\left (\frac {1}{(u-(m+in)\varpi)^2}-\frac {1}{((m+in)\varpi)^2}\right)$ 。这样就不必担心交换各项引起的问题。这与 Gauss 的 $M (u)$ 本质是一样的。

• (Eisenstein) 这位曾经备受 Gauss 赞扬的天才学生关于椭圆函数的研究在他死后几乎被人忘得干干净净。直到 1976 年 Andre Weil 才把 Eisenstein 的研究从遗忘中唤醒。Eisenstein 的二重求和的过程定义为 $\lim_{X\rightarrow\infty}\sum_{x=-X}^{X}\lim_{Y\rightarrow\infty}\sum_{y=-Y}^{Y}$ , 求和与极限不能随意变换顺序。二重积的处理是类似的。我们后面还会提到这种求和方式。

Gauss 的探险还在继续。根据 Gauss 全集第三卷和第十卷的内容，Gauss 似乎试图利用无穷乘积和双纽线函数的加法定理给出一些非平凡的等式。我们来证明其中的两个。

命题：$\begin {align} M ((1+i) u)&=(1+i) M (u) N (u),\\N ((1+i) u)&=\sqrt {N (u)^4-M (u)^4}\end {align}$ 。 [注：这个命题来自 Gauss 全集第三卷名为Elegantiores Integralis $\int\frac {\mathrm {d} x}{\sqrt {1-x^4}}$ Proprietates的未发表手稿 (题图即为此手稿的一部分)。文章中没有对命题的证明。Leiste 记录中有与这两个公式类似的公式，但是并不正确。两者使用的记号也不相同，前者使用的是年代更靠后的记号。]

证明 (梗概)：第一个等式的证明是 $M (u),N (u)$ 无穷乘积表达式的推论。注意到 $\frac {m+in}{1+i}=\frac {(m+n)+i (n-m)}{2}$ , 而 $m+n,m-n$ 具有相同的奇偶性，从而导出这一结论。第二个等式可以由双纽线函数的加法定理导出。根据加法定理， $s ((1+i) u)=\frac {s (u) c (iu)+c (u) s (iu)}{1-s (u) s (iu) c (u) c (iu)}$ 。再根据 $s (u),c (u)$ 的定义，我们有 $s (iu)=is (u),c (iu)=1/c (u)$ 。代入加法公式化简得到 $s ((1+i) u)=\frac {(1+i) s (u)}{\sqrt {1-s (u)^4}}$ 。所以我们有

$\frac {M ((1+i) u)}{N ((1+i) u)}=\frac {(1+i) M (u) N (u)}{\sqrt {N (u)^4-M (u)^4}}$ 。这样第二个命题也得到了证明。

根据同样的推理，我们立刻可以得到 $M ((1-i) u)=(1-i) M (u) N (u)$ 。所以 $M (2u)=M ((1-i)(1+i) u)=2M (u) N (u)\sqrt {N (u)^4-M (u)^4}$ 。根据 Fagnano 的倍乘公式，我们有 $\frac {M (2u)}{N (2u)}=\frac {2M (u) N (u)\sqrt {N (u)^4-M (u)^4}}{N (u)^4+M (u)^4}$ 。因此我们得到了 Gauss 写在 Leiste 算术书 66 页的公式

命题：$N (2u)=N (u)^4+M (u)^4$ .

[Gauss 还写下了大量 $M (u),N (u)$ 的类似公式，他有可能是由加法定理导出这些公式的]

Gauss 借助 $N (\varpi/2)$ 的值，可以得到 $N (\varpi)\approx4.81048$ 。在 Leiste 笔记的 71 页，他计算了 $\log N (\varpi)\approx \log 4.81048\approx1.5708$ 。为什么它这么像是 $\pi/2$ ? 这就引出 Gauss 1797 年 3 月 29 日的日记对此的评论：

...quod maxime est memorabile, cuiusque proprietatis demonstratio gravissima analyseos incrementa pollicetur.……这是最引入注目的，证明此性质会带来分析学极大的进步。

这是 Gauss 1797 年的日记中关于椭圆函数的最后一条记录。下一条记录在一年多后，他彻底解决了自己的疑问。

Gauss 3 月 21 日的日记内容至此可以这样解释：

我们已经知道，等式 $\frac {1}{u^2}+\sum_{m,n\in\mathbb {Z}}{}^{'}\left (\frac {1}{(u-(m+in)\varpi)^2}-\frac {1}{((m+in)\varpi)^2}\right)=\frac {1}{s (u)^2}$ 是成立的。我们可以通过对比等式两侧在 $u=0$ 处 Laurent 级数的系数而得到 $\sum_{m,n\in\mathbb {Z}}{}^{'}\frac {1}{(m+in)^{4k}},k>0,k\in\mathbb {Z}$ 的值。但是这里就隐藏着另一个 Basel 问题： $\sum_{m,n\in\mathbb {Z}}{}^{'}\frac {1}{(m+in)^{4k}}$必然是 $\varpi^{4k}$ 的有理数倍。如果 Gauss 知道 Euler 关于 zeta 函数的工作，那么，在这一点上深钻下去一定会把他带到椭圆曲线的 L-函数。Adolf Hurwitz是捡起这个问题的第一人，而他捡起这个问题时，已经是 Gauss 写下日记一百年后的事情了。