丢番图方程和它在数论中的另一位亲戚——素数——一样善于伪装。现代数论研究的一位老将Peter Swinnerton-Dyer在一篇名为“DIOPHANTINE EQUATIONS: PROGRESS AND PROBLEMS”的综述里对数值计算丢番图方程的解写了一些相当中肯的意见：

Progress in mathematics usually means proven results; but there are cases where even a well justified conjecture throws new light on the structure of the subject. (For similar reasons, well motivated computations can be helpful; but computationsnot based on a deep feeling for the structureof the subject have generallyturned out to be a waste of time.)

文章明确表示：如果对相应的丢番图方程的结构没有足够的了解，那么计算很多时候都是徒劳无功。为什么这么说呢？

1)三个整数的立方和。怎么样找到三个整数 (三个整数不必符号相同) 的立方和使之等于给定的整数 $a$ 呢？利用同余关系很容易证明如果 $a$ 除以 $9$ 余 $4$ 或 $5$，那么无解。那么剩下的整数呢？下面这个例子属于 Lyons 大学的 Sander G. Huisman (https://arxiv.org/abs/1604.07746)。

丢番图方程

$$x^3+y^3+z^3=74$$

的最小解是

$$(66229832190556, 283450105697727,-284650292555885)$$

看到这个问题首先想到编个循环求解的人可以想象一下跑 $10^{20}$ 个以上循环，并且计算的数字平均在 $10^{40}$ 左右的感受。

2)Congruent Number(所谓的同余数，其实和同余式并没有非常直接的关系) 找一个有理数 $d,$ 使得 $d-a,$ $d,$ $d+a$ 都是有理数的平方。其中 $a$ 是一个给定的正整数。这个问题的另一个形式是找一个三边长都是有理数的直角三角形，使得它的面积等于给定的正整数 $a$。

Fermat 的无穷递降法成功地帮他否决了 $a=1$ 时解的存在。对于某些整数 $a$，找到相应的等差数列或直角三角形是比较容易的，譬如说 $a=6$. $a=5$ 就困难一些。对于某些 $a$，找到解比证明解存在要困难的多。最出名的例子是 $a=157$ 的情况。找到解的第一人是 Don Zagier. 他找到的解是：

$$d=\frac {a^2}{b^2}.$$ $$a=224403517704336969924557513090674863160948472041$$ $$b=2\times 8912332268928859588025535178967163570016480830$$

分子和分母都是天文数字！

印证 Peter Swinnerton-Dyer 观点的例子数不胜数，更多有趣的例子可以参见 https://www.zhihu.com/question/37164066/answer/71589759

数学史上不缺乏这样的例子：重要的理论或是解决问题的思路几乎同时被几个人发现，例如 Poincare 与 Klein 在 19 世纪 80 年代在模形式方面的竞争。Euler 猜想的解决也不例外。解决问题的关键几乎同时由三个人获得：Max Planck 研究所的 Don Zagier, Harvard 的 Noam Elkies 和 ASU 的 Andrew Bremner. Don Zagier 在文章里回忆了自己当年的发现：

1986 年下半年 Don Zagier 本人在 Berkeley 的数学科学研究中心作了一次关于丢番图方程的讲座。讲座后有一位姓 de Vogelaere 的人询问 Zagier 是否知道 Euler 的猜想，并且和 Zagier 分享了一些自己的想法。

de Vogelaere 的出发点是下面这个代数等式：

$$(m^2+mn+n^2)^4=(mn)^4+((m+n) n)^4+(m (m+n)(m^2+mn+2n^2))^2$$

Zagier 本人只说这是 1895 年由 Escott 发现的等式。但是看过 Elkies 本人的文章后，我个人的猜测是：de Vogelaere 本人看过L. E. Dickson的名著History of the Theory of Numbers. 上面的等式出现在这本书第二卷第 658 页。等式的发现者 E. B. Escott 大概是 Umich 的一位教授，该等式发表在 1899 年的一本杂志上。如果 Dickson 不记载这个等式，大概它就会永远被人遗忘。

de Vogelaere 注意到，等式里只有等号右边的最后一项形式上不是四次方数。问题在于，能不能找到一组整数 $m,n,$ 使得 $m (m+n)(m^2+mn+2n^2)$ 是非零的平方数呢？答案是不能。这是可以由椭圆曲线的相关理论推出的结论。不过 de Vogelaere 找到的等式不止上面那一个，他找到的一族等式可以这样表示：

$z,x,y$ 均为关于变量 $u,v$ 的有理系数二次齐次多项式，$t$ 是关于变量 $u,v$ 的有理系数四次齐次多项式。它们满足关系

$$z^4-x^4-y^4=t^2.$$

de Volgaere 本人的问题是：

1) 有没有系统生成关于 $u$，$v$ 的有理系数多项式 $z$, $x$, $y$ 的方法？

2) 如果能找到这样的多项式 $z$, $x$, $y$, 能否找到整数 $u$, $v$ 使得 $t$ 是不为 $0$ 的平方数？

$z,x,y$ 均为关于变量 $u,v$ 的有理系数二次齐次多项式] 这个条件暗示了 $z,x,y$ 之间存在一些关系。利用消去法，不难得到，$x,y,z$ 满足 $Q(x,y,z)=0$, Q 是关于 x, y, z 的二次有理系数齐次多项式。反过来，给定一个二次有理系数齐次多项式 $Q(x,y,z)$，不一定能找到有理系数二次齐次多项式 $x(u,v),$ $y(u,v),$ $z(u,v)$ 使得 $Q(x,y,z)=0$. 但是只要 $Q(x,y,z)=0$ 所表示的二次曲线上有一个有理点，我们就可以用与球极投影类似的方式，生成多项式 $x$, $y$, $z$.

一个自然的问题是：如果 $Q (x,y,z)=0$, 那么 $z^4-x^4-y^4=t^2$ 代表了什么样的含义呢？注意到 $t(u,v)$ 的零点正对应 $z^4=x^4+y^4$ 与 $Q (x,y,z)=0$ 的交点，而且两条曲线每一个交点都是二重的。这意味着，两条曲线相切于四个点。我们再利用一次消去法，可以得到 $t(u,v)$ 可以表示为 $x(u,v),$ $y(u,v),$ $z(u,v)$ 的有理系数二次齐次多项式。记这个多项式为 $P (x,y,z)$。由我们的推理，可以得到，只要

$$Q (x,y,z)=0$$

那么可以找到二次 (有理系数) 多项式

$$P (x,y,z)$$

使得 $z^4-x^4-y^4-P^2 (x,y,z)=0$。

这个事实说明什么呢？说明 $z^4-x^4-y^4-P^2 (x,y,z)$ 可以分解为 $Q(x,y,z)$ 和另一个有理系数二次齐次多项式 $R(x,y,z)$ 的乘积。也就是

$$z^4-x^4-y^4=P^2-QR$$

Zagier 注意到，等式右面可以看做是二次型 $Qs^2+2Pst+Rt^2$ 的判别式。做一个线性变换 $s'=as+bt$, $t'=cs+dt$，$ad-bc=1$ ($a,b,c,d$ 全是整数), 那么得到关于 $s',t'$ 的二次型判别式并不发生变化。不过新的二次型的系数 $P', Q', R'$ 是 $P，Q，R$ 的线性组合。这是 Gauss 已经玩的很熟练的技巧。借用这个古老的技巧，我们就可以得到一族多项式 $P$，$Q$，$R$，从而回答了 de Vogelaere 的第一个问题。

Remark 1. 不难得到 Escott 等式对应的 $P,$ $Q,$ $R$ 分别为

$$P=z^2-(x-y)^2$$ $$Q=x^2+y^2-xy+xz-yz$$ $$R=2 (x^2+y^2-xy-xz+yz)$$

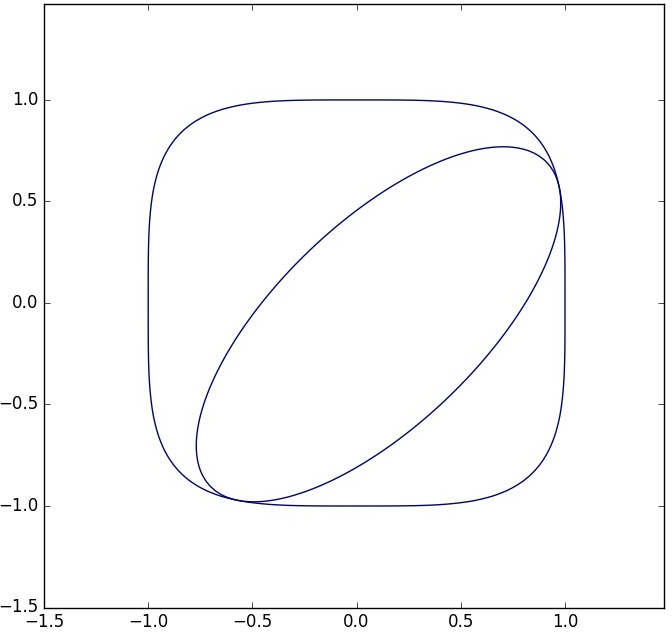
文章的插图对应的就是由这一组 $P,$ $Q,$ $R$ 生成的曲线 $Q'=0$ 与 $z^4=x^4+y^4$ 对应的代数曲线的图形。可见两条曲线切于两个实点，还有两个切点是虚的。

Remark 2.Andrew Bremner的方法有点诡异。

$$z^4-x^4-y^4=t^2$$

可以恒等变换为

$$2 (z^2+x^2)(z^2+y^2)=(z^2+x^2+y^2)^2+t^2$$

这个等式存在的一个充分条件是

$$\theta (x+iz)(y+iz)=t+i (x^2+y^2+z^2), \theta\in\mathbb {Q}(i), \vert \theta\vert=2$$

分开实部虚部，消去 $x,y,z$ 中的变量，也可以得到 $t$ 为某两个变量 $u,v$ 的四次齐次函数。这样就抵达了 de Vogelaere 的第二个问题。但是 Andrew Bremner 本人并没在这个问题上继续深钻下去。

Remark 3.Zagier 用线性变换构造出的一族 $x (u,v),y (u,v),z (u,v)$ 覆盖了 $z^4-x^4-y^4=t^2$ 上的每一个整点。这可以保证 $z^4-x^4-y^4=t^2$ 的每一个整数解都可以由这组构造得到。