人们常说数学就是关于如何理解各种各样的模式，而这些模式使得数学变得美丽多彩。然而本文是关于数学怎样可以用来产生或模拟缺乏模式的随机性。令人惊讶的是，我们将会看到，很难产生随机行为，同时更难判断何时我们已经成功产生随机行为。某种意义上，产生随机性这句话听起来都有点刺耳。

本文将专注于构造随机数。为什么要构造随机数的原因很多。千百年来，人们一直在使用随机性，比如抛硬币来决定某些命运或输赢。今天，人们也使用随机数搞彩票，以确定巨额资金的获得者。

当前，很多网络信息或信用卡信息需要通过安全确认，随机数就被用来形成加密密钥。另一方面，随机数也可以用来模拟真实世界的现象。例如，经营自动取款机网络的银行设计的软件，常常通过随机时间随机取款机来模拟客户访问自己的帐户来测试软件的功能。

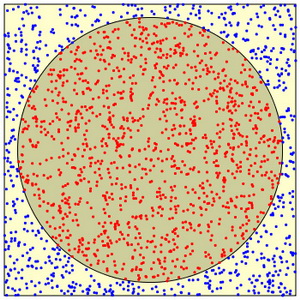
随机数的另一个应用是著名的蒙特卡罗算法。所谓的蒙特卡罗方法对极难获得精确解的问题用随机数方法来获得数值逼近。例如，假设我们不知道单位圆的面积公式。如何计算它的面积呢？我们可以把单位圆放进一个面积已知的正方形里面（如下图），并在正方形上随机加点。落在圆内的点数的百分比应该近似于圆的面积和正方形面积的比。下图显示了随机放在一个边长为2.2的正方形上的2000个点，其中1308个点落在圆内。圆的近似面积等于正方形的面积4.84乘上1308/2000，结果是3.16536（当然，圆的精确面积是$\pi\approx3.14159$）。这已经比较接近单位圆的面积值了。如果撒的点更多，比如说10000个，得到的近似值将更精确。

随机数来自何处？

我们大多数人对随机数已有一个直观概念，但是正如我们将要看到的，随机数是一个很难准确回答的问题。简单地说，我们应该无法使用已经看到的数来预测接下来的数。例如，你可能希望掷一个理想骰子。每掷一次，1至6之间的每一个数字出现的可能性一样。如果我们掷了很多次，我们可以期望看到六个可能性的每一个大概是时间的六分之一。此外，如果我们每次扔两次骰子，得到一对结果（i，j），i和j取1到6间的一个数，这将出现了36个可能的对子。数数每一对结果出现的个数，我们会期望36种可能对的每一个出现的频率大致相等。然而，即使前一千次都是“1”出现，掷第1001次时，1至6之间的每个数字显示的可能性还是一样。

乍一看，产生随机数看起来像一个简单的事情，你可能会认为可以通过例如有意识地写上0和1组成的序列就能做到这一点。假设你写了一个一百个0和1的序列，它可用来被本文后面给出的一些测试来分析。如果你的序列通过这些测试，它与真正的随机序列共享几个性质。但是，你很可能会发现很难写出一个序列通过这些测试。人类试图通过创建“随机行动”来产生随机序列这件事是有困难的。

自然现象极有可能产生真正的随机数序列。网站HotBits记录放射性粒子衰变时所产生的随机序列。例如，两个衰变之间的时间被记录下来并与下两次之间的时间相比。如果第一次时间比第二次短，记“0”；如果第一次比第二次长，则记“1”。这种方式产生了一系列随机位，连接在一起形成随机整数。另一个网站Random.org以类似的方式记录大气噪声的幅度。

一个有趣的问题是：无理数$\pi$给出的数字是否形成一个随机序列？在看过它前面上万亿数字后，数值的证据显示答案有可能是肯定的。但严格的结论还很难仅凭观察得出。

随机数产生器

现实生活中，许多应用需要我们能够在计算机内创造有效的随机数。这听起来似乎是不可能的：电脑仅仅执行一系列的指令，其输出由输入决定。由于人们给计算机提供指令和输入、输出也应由人们的选择决定。那怎么能使这样的一个序列数是随机的？

答案是否定的。可我们能做的是使用一个程序来隐藏我们的足迹，使得生成的数列给人以随机的错觉。更确切地说，我们希望计算机生成的数共享真正的随机序列所享有的许多属性。由于生成的不是真正的随机数，这样的程序通常被称为伪随机数产生器，但是我们按照惯例使用随机数产生器这一术语。本文的讨论很多取自参考文献中给定的Donald Knuth在《计算机程序设计艺术》第2卷中的论述。

计算机的创始人之一冯•诺伊曼提出了下述的随机数产生方法。假设我们想产生一个8位数的随机序列，我们先给定一个初始值$X_0$，下一个随机数$X_1$取自$X_0^2$的中间八位数。例如， 给定$X_0$=35385906，这时$X_0^2$=1252162343440836，去掉其首尾各4位数，得到下一个数$X_1$=16234344。 这样重复做几次，就得到下表：

$X_0$	$16234344$
$X_1$	$55392511$
$X_2$	$33027488$
$X_3$	$81496359$
$X_4$	$65653025$
$X_5$	$31969165$
$X_6$	$02751079$
$X_7$	$56843566$
$X_8$	$19099559$
$X_9$	$79315399$

乍看之下很难发现这些数的模式，我们可能认为这是找到随机数的一个合适方式。换句话说，我们已经通过一个确定性的过程产生了随机感觉。然而，进一步的研究表明，这不是一个好的随机数产生器。序列中的每一项只取决于前一项，并且只有有限多个可能的项（这个序列少于$10^8$个不同的可能）。这意味着，序列将不可避免地重复，它可以在相对短的循环中陷入困境。举例来说，如果31360000这个数出现在序列的某一处，99次迭代后我们又将见到它。

上述的中间平方法可能会给人们一个错觉，即计算机在执行一系列很多的、彼此无关的、随机的操作。事实上，Knuth构建了一种算法，用13个“奇特”的步骤产生10位数序列中的下一个，但可以发现这是一个非常糟糕的产生随机数的方式。下面我用看上去是“随机”的运算创建了一个简单的算法来生成两位数序列。

• 以两位数字为$d_1 d_0$的数开始。

• 形成一个新数$r=10 -（d_1+ d_0）$(模10)。

• 形成一个有三个数字的数$s=d_1 r d_0$。

• 令$t=\sin \left(e^s\right)$。形成一个新的有两位数字$e_1 e_0$的数，其中$e_i$是$t$在小数点后第$d_i$位的数字。

• 如果$e_0$大于5，更换为$10 - e_0$。

• 现在计算$(e_1+1)/(e_0+1)$的反正切函数值，此值小数点后的前两个数字就是新生成的两位数。

奇怪的是，该算法产生一个短循环：91，96，46，1，64，73，72，91，...，且大部分初始值$d_1d_0$都把我们引向这个循环。正如Knuth所写：“这个故事的寓意是，随机数不应由随机选择的方法产生。”

线性同余产生器

令人惊讶的是，漂亮的伪随机数产生器居然来自Derrick Lehmer于1949年推出的线性同余法。在这里，我们选择$m$为模，$a$为乘数，$c$为增量，$X_0$为初始值。然后我们由

$$X_{n+1} = f(X_n) = (a X_n + c) \; \; \mbox{模} \; m$$

形成序列中的下一项。

乍一看，很难相信这会产生随机性。请记住，我们希望序列的每一项独立于它的前一项。使用一个线性函数我们真的可以做到这一点吗？事实证明这是可以的，只要我们能适当选择a，c和m值。

当然，只有有限个的可能的数0,1,2,...,m-1会出现，且因为每一数由前一数确定，该序列将不可避免地形成一个重复循环，其周期不比$m$大。如果这个周期短，序列将很快开始重复，这对试图模拟一个随机序列是不明智的。然而，下面的定理说明我们如何能让周期达到最大长度$m$，也就是说前m个数不会出现重复。为了表达这个定理，可以简写$b=a-1$。

序列$\{X_n\}$的周期为$m$当且仅当

• (1) $c$和$m$是相对素的。

• (2) $b$是$m$的每一个素因子的倍数。

• (3) 如果$m$是$4$的倍数，则$b$是$4$的倍数。

例如，选择$m = 3^5 \cdot 5 \cdot 7, b = 3 \cdot 5 \cdot 7$和$c=64$产生一个循环数列，其周期是$m=8505$。我们因而有

$$X_{n+1}=(106 X_n + 64) \; \; \mbox{模} \; 8505.$$

下面所示的是用这个产生器生成的最初一些点$(x, f(x))$。正如你所看到的，他们似乎被随机放置。

通常情况下，整数在计算机中使用32比特来表示，所以很自然选择m的值靠近$2^{32}$。合适选择a和c，我们的序列可以遍历计算机能表示的最大整数后才开始循环。

注意到$a = c = 1$满足这一定理的假设。然而，这种选择产生的序列

$$X_0, X_0 + 1, X_0 + 2, X_0 + 3, X_0 + 4, \ldots $$

显然不是随机的。所以要使用这种方法来创建随机数，除了最大的周期条件，我们还需要另外一个条件。我们现在要描述的第二个条件将叫做该序列的效能，定义为满足$b^s = 0$ 模 m的最小整数s。

为了理解这个数s，以$X_0 = 0$（因为序列周期为m,最终将遇到0）开始，并注意到

$$\begin{array} X_1 = (a X_0 + c) \; \; \mbox{模} \; m = c \\ X_2 = (ac + c) \; \; \mbox{模} \; m \\ X_3 = (a^2c + ac + c) \; \; \mbox{模} \; m \\ X_n = (a^{n-1}c + \cdots + ac + c) \; \; \mbox{模} \; m \\ X_n = ((a^n - 1)c / b) \; \; \mbox{模} \; m \end{array}$$

假如我们展开$a^n - 1 = (b + 1)^n -1 $，则得到

\[ X_n = c \left( n + \left(\begin{array}{c}         n \\         2 \end{array} \right) b + \cdots +              \left(\begin{array}{c}         n \\         2 \end{array} \right) b^{s-1} \right) \; \; \mbox{模} \; m . \]

如果效能是1，那么我们有$X_n = (c n) \; \mbox{模} \; m$。这个顺序肯定不是随机的。

如果效能为2，则$X_{n+1} - X_n = (c + cbn) \; \mbox{模} \; m$。换句话说，逐项之间的差以可预见的方式展现，这样的序列也不能被认为是随机的。

继续这一思想表明，我们发现需要的效能应比较大才能实现随机性的感觉。实验表明，效能至少为5才能保证产生有用的随机数。然而，效能5的线性同余序列仍不能保证是随机的。

在上面的例子中我们有$m = 3^5 \cdot 5 \cdot 7, b = 3 \cdot 5 \cdot 7$，它产生具有最大周期及效能为5的线性同余序列（下面左图列出最初的一些点）。相比之下，如果取$m = 3^5 \cdot 5 \cdot 7, b = 3^5 \cdot 5 \cdot 7$，我们有最大周期但效能为2的线性同余序列（下面右图列出最初的一些点）。

尽管线性同余序列的定义相对简单，但所产生的伪随机数在许多应用上都足够好。事实上，计算机编程语言如Java提供的随机数通常都是由线性同余产生器生成。初始值$X_0$的选择往往采取以毫秒为单位表示的当前时间。

除了线性同余方法之外，另外的方法也可被用来产生随机序列。两个想法浮现在我脑海中。首先，我们可能会选择一个二次函数，而不是一个线性的。Robert Coveyou建议用函数

\[ X_{n+1} = X_n (X_n + 1) \; \; \mbox{模} \; 2^e , \]

并证明它产生足够的随机数。

此外，我们可以考虑使用比前一项更多的项来产生序列中的下一项。一个例子是滞后的Fibonacci序列，由Gerard Mitchell和Donald Moore在1958年提出：假设一个序列的前55个随机数被生成了（比如由一个线性同余产生器生成），函数

\[ X_{n+1} = (X_{n-24} + X_{n-55}) \; \; \mbox{模} \; m \]

可用来生成后面的数，表达式中出现的24和55这两个参数是经过仔细研究后选取的，它们可以保证该序列有一个适当长的周期。

我们如何识别随机数？

我们需要一些方法来鉴定随机数方法的质量。本节将描述几个很重要但仍有点不足的测试。我们先描述一个简单测试并看它是如何工作的。

让我们考虑一种简单情形，生成的数字不是0就是1。有32= $2^5$个可能的五元数字序列，五元数的每个组取决于有多少个0，即有0，1，2，3，4，5个0中的一种。下表显示了这32个五元数中有$i$个0的个数$n_i$，和有$i$个0的序列的概率$p_i$:

$i$	$n_i$	$p_i$
$0$	$1$	$1/32$
$1$	$5$	$5/32$
$2$	$10$	$10/32$
$3$	$10$	$10/32$
$4$	$5$	$5/32$
$5$	$1$	$1/32$

我们现在介绍的方法被称为卡方检验。给定由0和1构成的序列$\{X_n\}$，将它分解成r个连续五项组成的不相交组，用$r_i$记有$i$个0的小组个数。如果我们的顺序是随机的，应该有$r_i = r p_i$，这样我们就可以由计算$(r_i - r p_i)^2$来衡量我们的序列与随机序列怎样不同。由于$p_2$远远大于$p_0$，我们应该期望$r_2$远远大于$r_0$且相应的误差应该更大。为了避免过分侧重于6个可能性中的任一个，我们用$r p_i$来除$(r_i - r p_i)^2$，形成生成序列与随机序列相比的卡方统计：

\[ V = \sum_{i=0}^6 \frac{(r_i - r p_i)^2}{r p_i}. \]

例如，假设我们有

\[ r_0 = 10, r_1 = 46, r_2 = 95, r_3 = 107, r_4 = 60, r_5 = 15 \]

并算出V=4.835。为了解释这个数，对所有可能的0和1的长度为5r的序列算出V，并问多少序列有比V低的值。记这些序列占的百分比为p。当然，这事相当繁琐，但有一个不会在这里描述的一般理论来解救我们，使我们能够以相对简单的方式计算一个近似的百分比。在我们的例子中，我们发现大约p=56%的序列有较低的V值。

Knuth提出，我们的序列测试当p99%时失败，并当p90%时应用怀疑的眼光去看待它。想法是，如果p太高，那么它与随机序列相差太多而不被认为是随机的。如果p太低，则它与随机序列的统计数据太密切匹配，其特征与随机序列太相似了，因此也应被否定。

Knuth还建议对产生器所生成的不同序列于三个不同的时间测试。如果任何一个时间测试给出了可疑的结果，我们就不应该把这个产生器看作能生成足够的随机结果。以同样的方式，我们不妨多次重复测试，并确定p与均匀分布是否匹配；也就是说，我们期望p约10%的时间在0%和10%之间，约10%的时间在10%和20%之间，等等。

一些被广泛接受的测试集合被称为Diehard测试，我们在这里列出其中一些。一种方法要有资格作为一个有用的随机数产生器，它需要通过所有这些测试。通常地，通过一个测试并不能保证它会通过另一个测试。

• 频率测试：我们希望我们的数均匀分布，因此，如果数从0, 1, 2,..., m-1中而来，则每个数以大致相等的频率出现。在这种情况下，我们让$r_i$表示i在我们的序列中出现的次数，并注意到$p_i=1/m$。当然，非随机序列0, 1, 2,...也将通过这个测试。因此，我们会要求除此以外，每对连续元素(i,j)以相同频率出现。这里，我们让$r_{i,j}$表示数对(i,j)在序列中出现的次数，并注意到$p_{i,j} = 1/m^2$。这就是所谓的2-分布测试，并可以扩展到更一般的K-分布测试。

• 排列测试：给t选一小值，如t=3，将序列分解成连续t项组成的不相交的组，并假设每组里任意两元素不相等。有t的阶乘种方式给其中的元素排序，每一个的可能性是一样的。

• 游程测试：在这个测试中，我们计算“游程”的长度，游程意指序列中的部分项满足各项单调增加或单调减少。

• 间隙测试：我们确定一个范围值，如0, 1, 2,..., m/2，计算序列中分开这个范围内的两个数的那些项的个数。

• 扑克测试：我们将序列$\{X_n\}$的元素分解成连续五元素组，并计数我们有的“扑克手”个数。这些包括——都不同: abcde；一对: aabcd；两对: aabbc；三个一类: aaabc；满堂红: aaabb；四个一类: aaaab；五个一类: aaaaa。

• 生日间距测试：这个测试在1984年由George Marsaglia推出。把序列$X_n$的项看作生日，数0, 1, 2,..., m-1看作一年的天数。我们将研究生日间的间距。要做到这一点，首先将序列的项按非递减的$X_{(1)}, X_{(2)}, \ldots$排序，然后找到生日之间的间距$S_1 = X_{(2)} - X_{(1)}, S_2 = X_{(3)} - X_{(2)}, \ldots$。我们让$r_i$表示$i$作为一个间隔发生的次数。

谱测试

我们到目前为止已经研究的测试，可以通过序列输出来检查任何随机数发生器及其工作质量。而谱测试则通过研究整个期间产生器的输出，专为线性同余产生器设计的。首先，我们构造所有(x, f(x))的点集，其中f是定义产生器的函数。例如，如果m=8505及c=64，则我们有

注意到所有的点都位于一有限族的等距平行线上。事实上，仔细观察你会注意到有许多这样的包含所有点的平行线族。这是可以预料的，因为函数f(x)是一个线性函数。对于每一族线，我们可以考虑线之间的距离，并定义d为这些线族距离的最大值。线性同余产生器的精度则被定义为1/d。

下图中左图对应的产生器精度更大（它也有更高的效能），因为这族平行线之间的最大距离小于右边的。

$m = 8505$$b = 3 \cdot 5 \cdot 7$$c = 64$	$m = 8505$$b = 3^3 \cdot 5 \cdot 7$$c = 64$

为什么精度可以反映随机数产生器的质量呢？下图给出上面图形中的对应的一段时间内1/20个总随机点的分布。

因为所有的点位于同一族线段上，当精度大时，这族直线会紧紧地挤在一起。相反地，当一族直线彼此较分离，点出现的地方会出现较小的灵活性，因而会使序列出现较小的随机性。

谱测试也可用于其他维数。例如在三维时，我们可形成点集{x,f(x),f(f(x))}，注意到这些点位于同一族平面上，准确性则要用平面间的最大距离的倒数来刻画。

在低维情形下，有一个有效的算法可用来计算精度。事实上，对线性同余产生器而言谱测试已经是最好的：所有已知的好产生器都能通过谱测试，而所有已知的坏产生器都过不了谱测试这一关。

结论

本文想告诉大家的一个信息是：产生一个随机数序列不容易，也很难确定一个序列究竟有多么随机。另一方面，令人惊讶的是一个简单的线性函数竟然是产生随机数的最流行的方式之一。

1997年，Makoto Matsumoto和Takuji Nishimura研究发现了一个新的随机数产生器，他们命名为梅森绞扭器(Mersenne Twister)，它具有惊人的大周期$2^{19937} - 1$。虽然它在密码应用中被发现并不很安全，但由它产生的随机数却非常有效，现已被广泛使用。

参考文献

1. Donald E. Knuth, The Art of Computer Programming, Volume 2, Third Edition, Addison-Wesley, Boston. 1997. Knuth's book is an excellent, comprehensive reference. Start here if you are interested in learning more.

2. Stephen Park and Keith Miller, Random Number Generators: Good Ones are Hard to Find, Communications of the ACM, October 1988, Volume 31, Number 10, 1192-1201.

3. HotBits, Genuine random numbers, generated by radioactive decay.

4. Random.org, a site that provides random numbers obtained through variations in atmospheric noise.

5. The Diehard tests, maintained by George Marsaglia at Florida State University.

6. Statisticians Charge Draft Lottery Was Not Random, New York Times, January 4, 1970, page 66.

原文链接:	http://www.ams.org/samplings/feature-column/fcarc-random
作者:	David Austin，Grand Valley State University
翻译:	丁玖，密执安州立大学博士，南密西西比大学数学教授
校对:	汤涛，香港浸会大学数学讲座教授