胜出几率
某天本文第二作者发电邮告诉第一作者，说一位名叫Derren Brown的魔术师正在电视上介绍一个有趣的游戏。我们听到“魔术师”这个词时有点怀疑，但细察之后发现该游戏确有数学背景，也是概率中的有趣练习。
掷硬币 这样的一个随机序列。这里H是英文Head的第一个字母，而Head表示硬币正面的意思，T是Tail的第一个字母，表示硬币反面的意思。游戏规则是：自己选定序列第一次出现的那个玩家（玩家A是HHH，玩家B是THH），就成为赢家了。
赢的策略
这个概率问题已经有一段时间了，但并不广为人知。Walter Penney于1969年在《趣味数学杂志》(Journal of Recreational Mathematics)上的一篇文章中提到它。美国著名数学科普作家马丁•加德纳(Martin Gardner)随后在《科学美国人》杂志 (Scientific American)1974年10月刊号的“数学游戏”专栏里以及在后来的书《时间旅行和其他数学困惑》(Time Travel and Other Mathematical Bewilderments)中给了它更详细的描述。
当游戏比赛使用长度为3的模式时，不管玩家A选什么序列，玩家B总可选个能赢的序列。下面是对应于玩家A的8个可能选取时，玩家B在平均意义上能取胜的策略。（等一下我们将显示怎样计算玩家B的胜算几率）：
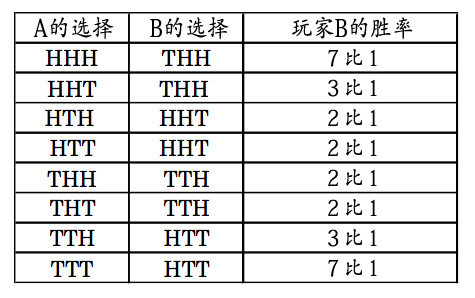表1：玩家A、B的选择和胜率 依据此表，对应于玩家A的HHH选取，玩家B选THH的胜算率为7/8，或87.5%；对应于HHT选取THH的胜算率为3/4，或75%；而对应于HTH选择HHT的胜算率为2/3，或66%，等等。无论玩家A选八种方案中的哪一个，玩家B总能选取一个三元序列以较大机会赢之。（你可以自己试一下这个策略，用自己的硬币或在网上玩这个游戏。）
石头–剪刀–布
从数学上讲，下述的东西被称作为一个传递关系：
用表1中游戏的话来说，则我们有
但这是Penney赌注游戏的真实命题吗？加德纳提出，这种传递关系在游戏中不成立。图1中的循环，说明里面有四个三元序列之间具有非传递关系。我们从表1所示的可能性中知道THH强于HHH，TTH强于THH，HTT强于TTH,HHT强于HTT,THH强于HHT。下图中的四个三元序列THH，HHT，HTT和TTH中没有最强者。
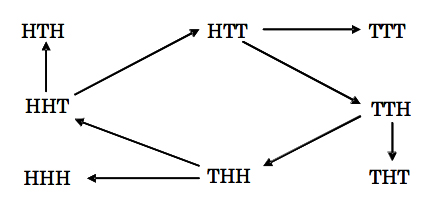图1：八个三元之间的关系。无论A选择哪一个三元，B总可以选择一个更好的三元，使自己获胜的机会大于A。 
石头剪刀布 相反，石头败给布，因此传递关系失效。同样，传递关系在Penney赌注游戏中不成立；如在石头-剪刀-布中那样没有必胜选手；任何一家先出招，另一家必有制胜的方法。
作出最强选择
现在让我们回到制胜战略。一旦玩家A已作出了选择，玩家B可以使用以下规则来选择三元序列，使得它更容易在玩家A的三元序列之前出现：
- 玩家B三元序列的第一元取为玩家A的三元中的第二元之不同者。假设玩家A选择了HHH。在这种情况下，玩家A的第二个元是H，其不同者显然是T，将它作为玩家B三元序列的第一元。
- 其次，把玩家A的三元序列的前两元取作玩家B的三元序列的后两元。在HHH的例子中用此法就得到玩家B的THH选取，这样在平均意义下可以7对1的比率打败玩家A。
- 玩家A的第三元不用被考虑。
我们可以验证表1中玩家B的每一个选择都遵循这个规则。但它仅对长度为3的序列有效———相同的算法不一定适用于其他长度。但我们能在马丁•加德纳的好书《时间旅行和其他数学困惑》中读到关于三元序列的这个策略，以及更长序列策略。而Daniel Felix更技术性的论文可以把这个制胜策略推广到任意长度的序列。
为了理解这个方法为何工作，让我们首先考虑当玩家A选取HHH时的策略。假设玩家A的三元序列不出现在抛掷硬币序列的最开始，而是在后来出现，例如在位置5,6和7处，即抛掷第5,6和7次时。我们要根据玩家A的三元序列的第一次出现时间给玩家B制定出位置4的符号，是H或是T。在我们的例子中，位置4必须是T，否则的话HHH最早就在位置4,5和6处出现，这和HHH最早出现在5,6,7处的假设矛盾。因此，在这种情况下，根据上述规则玩家B选取的三元序列THH将在玩家A的三元序列之前出现，即出现在位置4,5和6处。
这个法则失灵的唯一可能情形是当玩家A的三元序列HHH出现在最开始的时候———这就是为什么玩家B没有获胜的绝对保证；而A能获胜的唯一可能也就是HHH出现在最开始的时候。
什么是胜算率？
假设玩家A选HHH而玩家B按策略选THH。如果HHH出现在前三次抛掷，玩家A赢。在任何其他情形玩家B必赢。（正如我们上面所看到的，一个T必须在HHH首次亮相前出现，否则HHH就不是首次亮相！）前三次抛掷结果为HHH的概率为
这样
这里P表示概率的意思。因此，翻译成胜算率的说法就是玩家B的胜算率是7比1.
当玩家A选HHT时可以类似计算胜算率。这时，根据之前谈过的战略，玩家B应该选择THH（因为玩家A的第三元选取不影响玩家B的选择）。
一旦抛了一个T，则下面的序列中THH一定在HHT前出现。因此抛出HHT,或HHHT，或HHHHT，$\cdots$ 让HHT赢的概率为
这给出一个无穷和
运用几何级数求和可以得到
这个计算给出HHT赢的概率。因此THH赢的概率为
用胜算率的说法就是玩家B以3比1机会赢。
继续以这种方式，可以计算出表1中的每个选取的胜算率。
康威的算法
但是有一个更容易的方法可用来算出胜算率。著名数学家康威(John Conway)提出了一个作此事的漂亮算法。他引进了领先数的概念，用来作为表示图案重叠程度的指数。领先数也是关于给定模式在前一模式内重复程度的一个指标。
下面描述如何用康威算法来计算两个三元序列的领先数。首先，将一个三元序列放在另一个的上方，符号对齐，如我们下面对三元序列HHH和THH所做的那样。现在比较这两个三元序列：如果他们相同，则在第一个三元序列的上方放1，若不相同则放0：
| 0 | ||
| T | H | H |
| H | H | H |
第二步，去掉上方那个三元序列的第一元，将剩下的两元向左平移一个位置，和下方的领先元对齐。然后比较上方序列的两元与下方序列的前两元：如果它们相同，则在第一个序列的上方放1，若不相同则放0：
| 1 | ||
| H | H | |
| H | H | H |
重复这个过程直到上方序列的最后一元：
| 1 | ||
| H | ||
| H | H | H |
最后的汇总结果如下：
| 0 | 1 | 1 |
| T | H | H |
| H | H | H |
这样形成011三元数组是这两个三元序列之间的重叠指标，它能被读成二进制数。在我们的例子中，这个二进制数011等于十进制数3.
给定两个三元序列A和B，领先数可以给出玩家B计算胜算率的一个方式。用AA表示把三元序列A排在上方及排在下方位置上所对应的领先数，用AB表示把三元序列A放在上方而把B放在下方所对应的领先数，同样可定义BB和BA。那么，计算玩家B的胜算率的公式为：
在我们的例子中，A为三元序列HHH，B为三元序列THH。我们有
|
|
||||||||||||||||||||||||
|
|
将这四个值转换成十进制数（二进制数111等于7；000等于0；100等于4；而011等于3）并代入到表达式中，有
所以玩家B的胜算率为7，即指7对1的机会。这和表1中的第一项相符。进一步地，把玩家A的赢的概率记为p，玩家B记为q，则有
玩家A和玩家B都有八种可能选择，而且它们独立选取，而每个胜算率均可由康威算法自动产生，如表2所示。康威算法是非常强大的：它不仅可以给出序列长度为3的概率，而且对任何长度都可以，甚至对相异长度的序列也行。
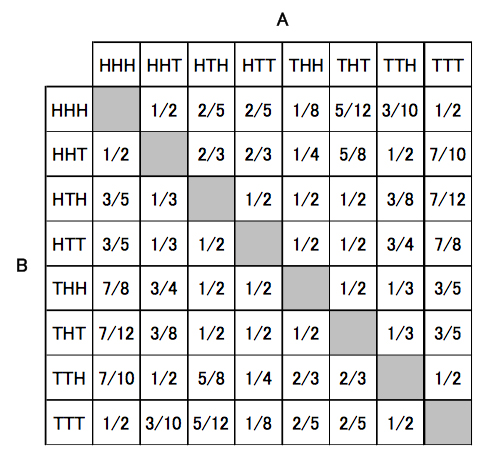表2：玩家A和B（序列的长度为3）获胜的概率。 把制胜策略用于玩牌
在前面几节我们察看了抛硬币正反面的Penney赌注游戏。我们一直在讨论如何将这些结果用到一个更为熟悉的场所，例如纸牌游戏。
一副扑克牌有52张牌，其中的26张黑色（黑桃和草花）和26张红色（红桃和方块）可以用来代替掷硬币正面或反面的结果。设B代表黑牌，R代表红牌，故抛硬币时的HHH对THH代之以玩牌时的BBB对RBB。
游戏的玩法如下：一次翻一张牌，放在一条线上，直到所选的三元序列出现。赢的玩家拿走所有已翻的牌，并赢得一个点。比赛用还未使用的牌继续进行，玩家拿回因自己的三元序列先出现而获得的已翻牌，这一过程直到所有的牌都用过。比赛优胜者是赢得点数最多的那个玩家。
随机纸牌 作为一个例子，让我们考虑BBB和RBB。作为硬币游戏的一个等价版本，BBB和RBB的概率分布为1/8和7/8，从而在单个对招中，RBB相对于BBB具有压倒性的胜算率7:1。然而，如果序列是RBR对应RRB，则RRB的几率只是2:1，这样的几率意味着不能保证在单一对阵中取胜。幸运的是，用一套扑克玩这个游戏通常会导致7到9次对阵，因为出现一次胜家一般不可能用尽52张牌，这将增加RRB的胜算率。例如，玩七次对阵RRB赢的概率是
其中$C_k$是二项式系数，它给出从7次对阵中取$k$次对阵赢的个数。
同样，玩一次有0.667胜率的玩家，对阵7次会有更明显的优势。玩7到9次对阵的纸牌游戏，单次有2/3胜率的玩家可以得到一个非常高的取胜概率。
我们相信，Penney游戏用来玩牌比掷硬币更合适。我们权且把本节中这个基于扑克牌的新游戏称作Humble-Nishiyama随机游戏，并希望我们的读者在家里拿一副牌试一试。
