David Austin/文
程晓亮 邬昊然/译

在本文中，我们将描述有理缠结和有理数之间的一一对应关系，并看到解有理缠结的过程与欧几里得算法之间的联系。

1.介绍

人们有时说数学就是认识和描述模式。令人惊讶的是，相似的模式似乎出现在不同的领域之中。在本文中，我们将研究绳结的拓扑结构，以此构建出有理缠结的模型。并了解如何用数论思想来描述这些缠结。特别地，我们将看到如何用欧几里得算法，这一最古老的算法对有理缠结的充分理解。

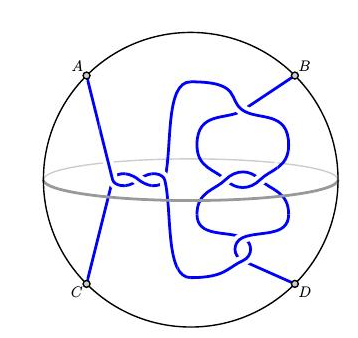
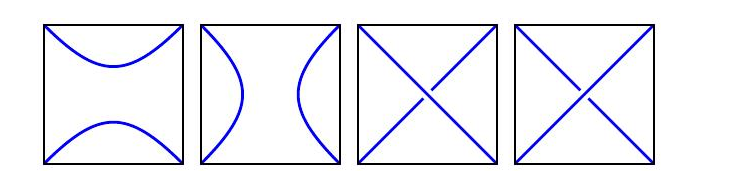
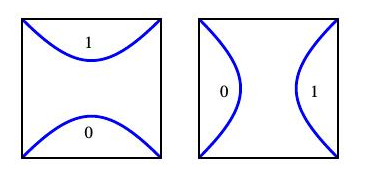
我们把几根绳子绑在一个三维球里，并使绳子的两端固定在球面上。下面的两条线是有理缠结，端点分别为$A,B,C$和$D$上相交，我们称之为2缠结。

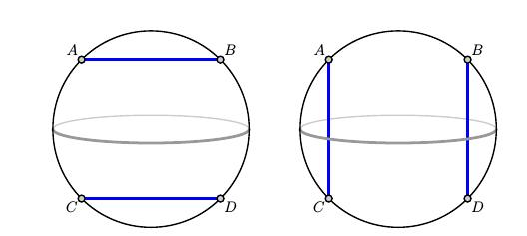
有两种基本的2缠结，简单地，由两股水平或两股垂直的缠结组成。

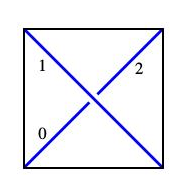
有理缠结是一种特殊的二元缠结，可以通过扭曲端点而解开为两个基本的缠结。例如，上面的缠结是二元缠结；如果我们把$A$和$C$缠绕在一起，就会得到下面的缠结。那么如何从这里继续解除。

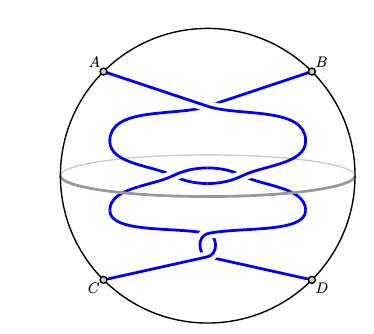
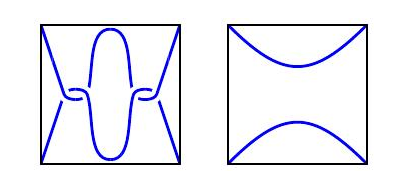
正如下面的例子所示，并不是每一种缠结都是有理缠结。例如，左边的两团乱在中间有一小结，这不是有理缠结；一个小实验表明出结论，右边的纠结不能通过扭转来解开。

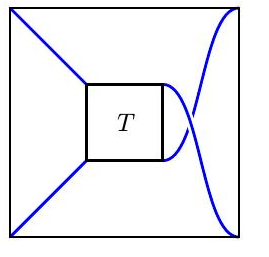
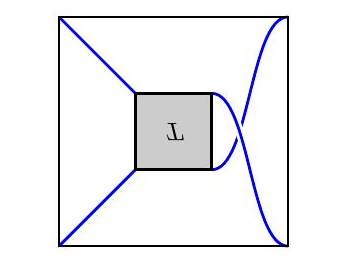
我们通常用绘制在“缠结盒”中的二维图形来表示缠结。

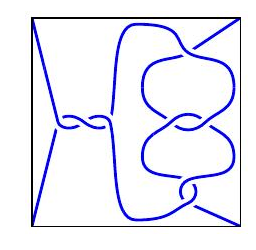
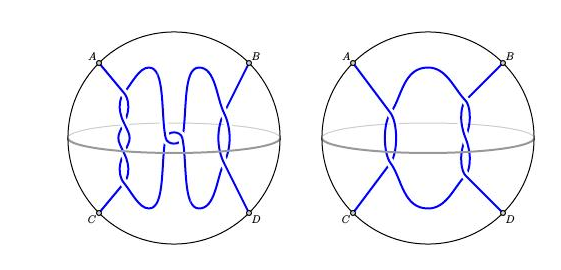
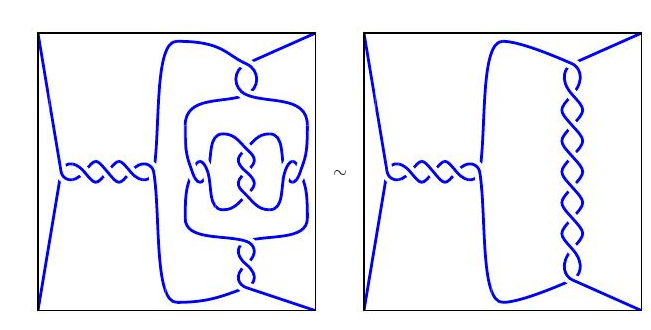
如果两个缠结的二维图形表示是一样的，则认为它们是等价的；简单地说，我们可以通过移动线而不需要交叉，也不需要移动端点，使一个缠结变形为另一个缠结。如果缠结$T1$和$T2$是等价的，我们写为$T1\sim T2$，像下面的两个是等价的：

康威认识到，在结的构造中，有理缠结作为基本单元，并使用它们来创建一个系统的结符号，形成了有11个或更少交叉点的结。

在本文中，我们将描述有理缠结和有理数之间的一一对应关系，并看到解有理缠结的过程与欧几里得算法之间的联系。

2.有理缠结上的操作

我们可以用一些自然的操作从旧的缠结中形成新的缠结。通过这种方式，我们将找到一种简单的方法来构造并且表示所有的有理缠结。

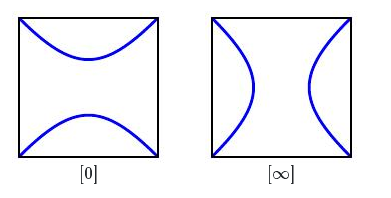
现在，我们将表示以下缠结$[0]$和$(\infty)$。

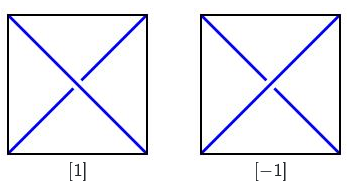
从$[0]$开始，根据转折的方向，我们可能会扭曲最右边的端点获取缠结$[1]$和$[−1]$。

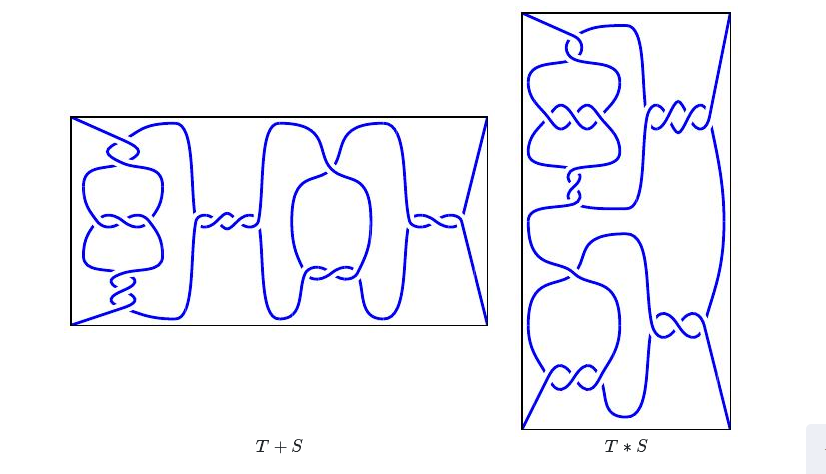
给定缠结$T$和S，

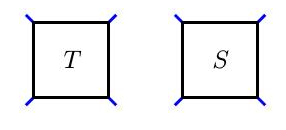
我们将定义操作

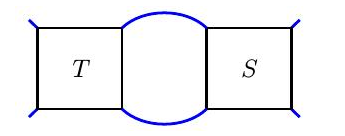
●加法：缠结$T+S$是

●乘法：缠结$T∗S$

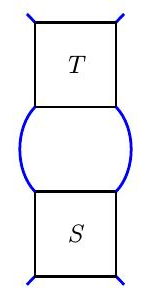
例如，如果$T$和$S$是

那么和式和积就是

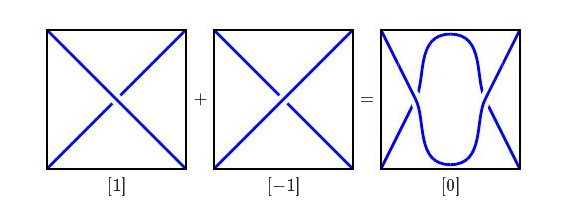
例如，我们也可以看到$[1]+[−1]=[0]$。

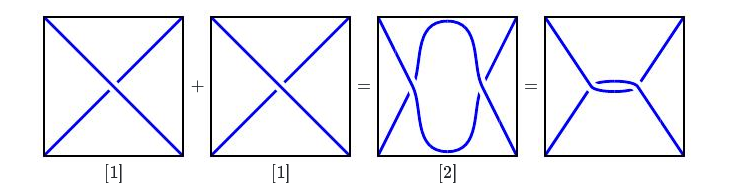
我们也可以定义$[1]+[1]=[2]$等等。

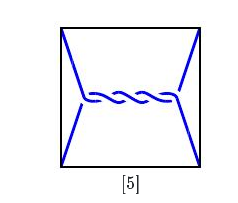
更一般地，我们定义$[1]+[1]+ \cdots +[1]=[n]$；例如，缠结$[5]$如下所示。

结果之后会更加明确，我们将表示$[1]∗[1]= 1 / [2]$。

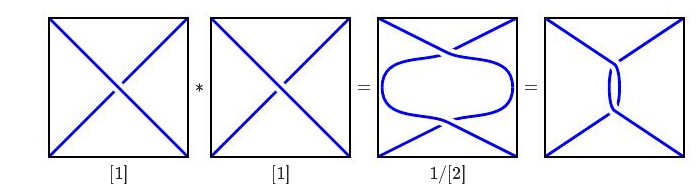
同样也有$[1][1]∗∗∗…[1]= 1 / [n]$。

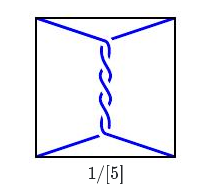
若$n = 0$，则$1 /[0]=(\infty)$。

使用这些操作，我们可以以标准形式编写有理缠结。我们开始与$[0]$和$[\infty)$和扭转对端点。例如，我们可以在顶部和底部旋转，然后在左边和右边旋转，等等。

最终，我们看到有理缠结可能会以扭曲的形式出现

$$\frac { 1 } { \left[ a _ { k } \right] } * \left( \cdots * \left( \left[ b _ { 3 } \right] + \left( \frac { 1 } { \left[ a _ { 1 } \right] } * \left( \left[ b _ { 1 } \right] + \frac { 1 } { \left[ a _ { 0 } \right] } + \left[ b _ { 2 } \right] \right) * \frac { 1 } { \left[ a _ { 2 } \right] } \right) + \left[ b _ { 4 } \right] \right) * \ldots \right) * \frac { 1 } { \left[ a _ { k + 1 } \right] }.$$

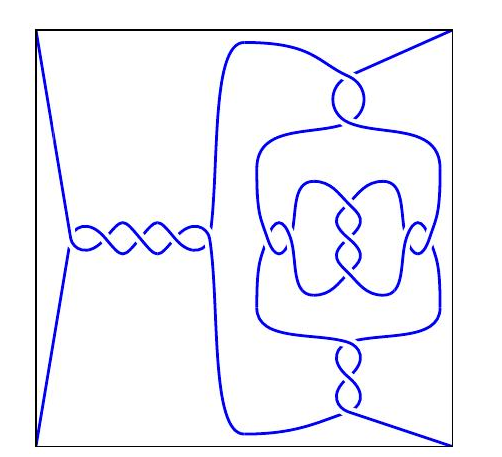
例如，这里是有理缠结 $[ 5 ] + \left( \frac { 1 } { [ 2 ] } * \left( [ 2 ] + \frac { 1 } { [ 3 ] } + [ - 2 ] \right) * \frac { 1 } { [ 3 ] } \right)$。

3.翻转和折叠

为找到一种简单的方法来构造所有的缠结，我们还需要观察更多的缠结操作。

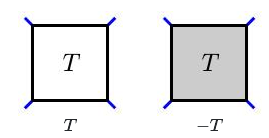
首先，我们可以通过将所有的下交叉道口改为上交叉道口来构造出新的缠结，反之亦然。这个操作下，缠结$T$成为缠结$−T$，我们将通过阴影覆盖缠结盒表示。这个符号是有意义的，因为$−[n] = [−n]$。

接下来，我们可以通过球的中心旋转，绕横轴旋转的缠结$T$来创建一个缠结$T^h$。

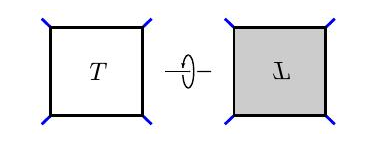
类似地，我们可以围绕一个垂直轴旋转$T$来获得$T^v$

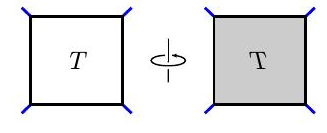
这一点，我们看到$[ \pm 1 ] + T \sim T ^ { h } + [ \pm 1 ]$，通过等价性质称为水平折叠。

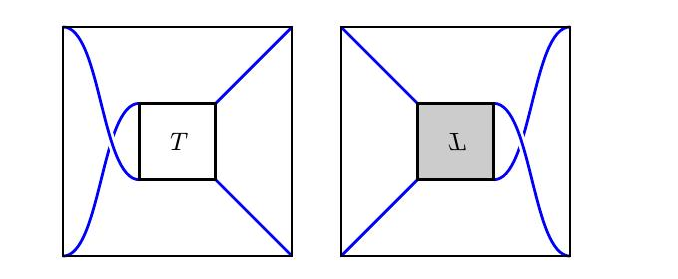
类似地，垂直折叠表明$[ \pm 1 ] * T \sim T ^ { v } * [ \pm 1 ]$

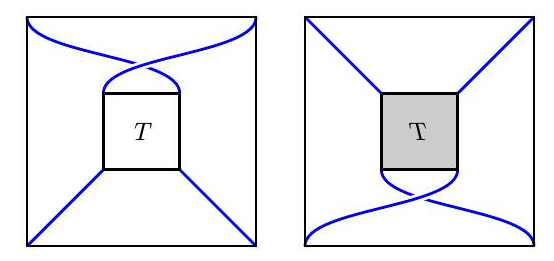
有了这些工具，我们现在可以解释一个相当令人惊讶的结果:

$$T ^ { h } \sim T \text { and } T ^ { v } \sim T.$$

对于上式的结果，注意，这个结果也适用于$[0],[\infty],[1],[−1]$。

我们现在做一个归纳的假设对于所有$n$个交叉点的缠结都成立。假设$T$是一个有$n$个交叉点的缠结，考虑$T+[1]$。

应用水平翻转给出。

根据归纳假设，$T ^ { h } \sim T$，也可以得到这样的结果$( T + [ 1 ] ) ^ { h } \sim T + [ 1 ]$。当然，还有其他一些情况需要检验，但它们的验证的方式大致相同。

因为我们之前验证过$[ \pm 1 ] + T \sim T ^ { h } + [ \pm 1 ]$，同理有
$$\begin{array} { l } { [ \pm 1 ] + T \sim T + [ \pm 1 ] } \\ { [ \pm 1 ] * T \sim T * [ \pm 1 ] } \end{array}
.$$

以这种方式，我们之前展示的有理缠结以扭曲的形式可以改写:

$$[ 5 ] + \left( \frac { 1 } { [ 2 ] } * \left( [ 2 ] + \frac { 1 } { [ 3 ] } + [ - 2 ] \right) * \frac { 1 } { [ 3 ] } \right) \sim [ 5 ] + \frac { 1 } { [ 8 ] }.$$

如下图所示:

这表明我们可以通过扭曲正确的端点和底部端点来产生所有合理的缠结。我们也可以通过介绍另一种关于缠结的操作过程来进一步说明这一点。给定一个缠结$T$，$T^r$通过旋转缠绕框$90^∘$逆时针方向得到。

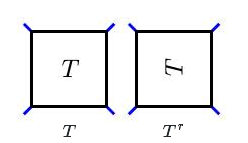
记作：$T * [ - 1 ] = \left( T ^ { r } + [ 1 ] \right) ^ { r }.$

画几幅图也可以看出，我们可以通过对$[0]$应用一系列加法和旋转操作过程来生成每一个有理缠结:

$$\begin{array} { l } { A : \boldsymbol { T } \mapsto T + [ 1 ] } \\ { R : \boldsymbol { T } \mapsto T ^ { r} } \end{array}.$$

例如，这里是由序列$AAARAAAARAA$造成的有理缠结。

4.缠结色彩和有理数

康威证明了有理缠结与有理数之间存在一一对应关系。在Kauffman和Lambropoulou之后，我们用缠结的颜色描述这些对应关系。

给定一个缠结图，缠结色的定义是在每个交叉点上用一个整数来标记每个圆弧，如下所示，在每个交叉处都有$a + b = 2 c$。

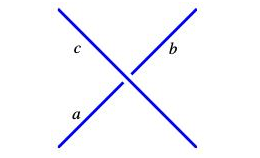
例如，下面的标签是一种颜色。

很容易看出每一团乱麻都有一个可能被着色的图表。首先，缠结的图$(\infty)$可能是彩色的。

执行操作$A$，意味着在右边增加一个扭转，增加一个交叉和一个有自由端的弧。着色规则告诉我们如何标记添加的弧，如下图所示。

类似地，将操作$R$应用到具有着色功能的缠结上会产生结果缠结的着色。

给出$T$的图的颜色

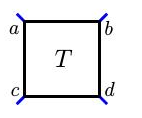
颜色矩阵将是$2×2$的矩阵

$$\left[ \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right]$$

组成的四个自由端。我们将有理数$f ( T ) = \frac { b - a } { b - d }$与缠结$T$联系起来。虽然这数字可能还不清楚，但它完全说明了这一缠结的特征。

例如，上述的缠结示意图的着色具有颜色矩阵

$$\left[ \begin{array} { l l } { 3 }&{ 10 } \\ { 0 }&{ 7 } \end{array} \right].$$

也就是说，$f(T)=7/3$和这个缠结有关。

事实证明，这个有理数既不依赖于缠结的图形，也不依赖于着色。以下两个事实可以解释这一点。

给定$T$的一个图的着色，任何其他图的着色矩阵都是相同的。

这是因为任何两个相同缠结的图都是由下图所示的Reidemeister运动序列联系起来的。

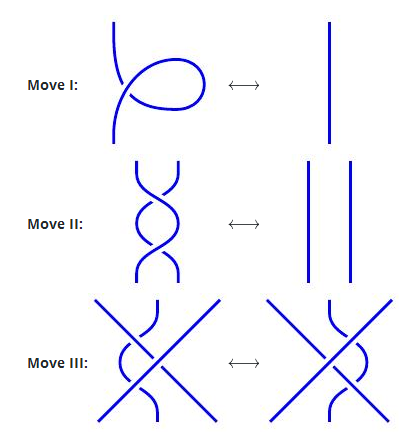
给定一个缠结图的着色，Reidemeister的任何移动都会产生一个新的图的着色，其颜色矩阵相同。下面的两个步骤说明了这一点；第三步也很容易检验。

如果$T$的一个图有颜色矩阵

$$\left[ \begin{array} { l l } { a }&{ b } \\ { c }&{ d } \end{array} \right],$$

则这个图的任何其他颜色都有颜色矩阵

$$\left[ \begin{array} { l l } { m a + n }&{ m b + n } \\ { m c + n }&{ m d + n } \end{array} \right].$$

考虑图中的任意两条弧。存在一个唯一的仿射变换$A(x)=mx+n$，它将一个颜色中的标签映射到另一个颜色中的标签。根据着色规则的线性，所有其他标签也必须与这个函数相关。

我们想要确定有理数在我们的操作$T \mapsto T + [ 1 ]$和$T \mapsto T ^ { r}$下是如何检验的。让我们首先考虑颜色矩阵。

下图是$T$和$T+[1]$的着色情况

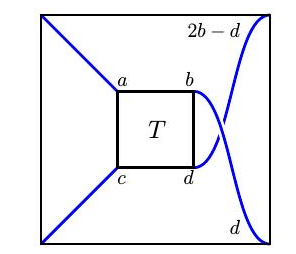
这说明$T+[1]$的颜色矩阵为

$$\left[ \begin{array} { c c } { a }&{ 2 b - d } \\ { c }&{ b } \end{array} \right].$$

$T^{r}$的颜色矩阵是通过旋转$T$的颜色矩阵中的元素得到的:

$$\left[ \begin{array} { l l } { b }&{ d } \\ { a }&{ c } \end{array} \right].$$

对于任何颜色矩阵，注意$a+d=b+c$是很有用的。这显然是真正的缠结$[0]$和$(\infty)$。从上面我们看到的，如果这个表达式适用于T，那么它也适用于$T+[1]$和$T^{r}$。因此，它对所有颜色矩阵都成立。

现在一个简单的计算表明了

$$\begin{aligned} f ( T + [ 1 ] ) &= f ( T ) + 1 \\ f \left( T ^ { r } \right) &= - \frac { 1 } { f ( T ) } \end{aligned}.$$

康威表明，$F$是一组一一对应的理性缠结和$\infty$附加的有理数集。

5.方块舞和欧几里得算法

康威描述了一款游戏，它能制造出缠结，然后只用操作$A$和$R$来解开它们。四个运动员站在一个正方形的四个角上。有两根绳子，每个人都握着一根绳子的一端。最初，绳索形成缠结$[0]$，玩家被要求从$A$和$R$的序列中构造一个缠结，然后他们被要求只用这些操作来解开缠结。

让我们从一个简单的例子开始：$T=[1]$。我们希望找到一个操作序列，将混乱的缠结解成$[0]$。如果我们应用A，我们就会得到$[2]$，这会让我们离目标更远。相反，我们应用$R$获得$[−1]$，然后得到$[0]$。也就是说，如果我们想要解开$[1]$，我们应该应用序列$RA$。

下图是对$[0]$应用$RA$的结果，这显然导致了$[0]$缠结。

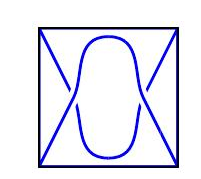
那么$[0]$怎么样？下面开始以下的过程：

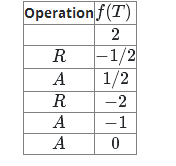
这表明$RARAA$会解开$[2]$，如下面的小框所示。

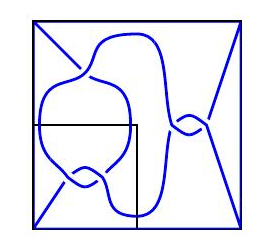
这些例子说明了下面的算法来解开缠结$T$：

如果 $f(T)>0$，应用$R$得到新的$T$。

如果 $f(T) < 0$，应用$A$得到新的$T$。

让我们看看这是如何在有理缠结$-17/7$中展开的。我们将有理数写成$p/q$的形式。

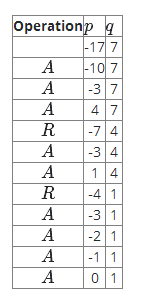
很容易直接证明出我们的算法是可以解出有理缠结$p/q$。然而，如果我们注意到我们的算法只是欧几里得算法的一种形式，它可以找到一对整数$a$和$b$的最大公约数，我们就可以达到同样的目的。

欧几里得算法中得到：$\operatorname { gcd } ( a , b ) = \operatorname { gcd } ( a - b , b )$。

如果我们假设$b>0$，我们可以把算法写成

如果$a> 0$，用$a-b$替换$a$。

如果一个$a < 0$，用$b$替换$a$，用$-a$替换$b$。

如果$a=0$，那么$b$就是最大公约数.

例如，如果$a=220,\,b=24$，我们有

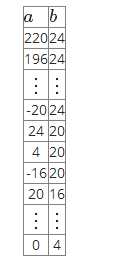
一些读者可能喜欢从有理数$p/q$算法开始，并生成一系列$R$和A，形成与$[0]$中的$p/q$相对应的有理缠结。

6.总结

这里隐藏着一个更丰富的故事。例如，可以定义另一个关于缠结的操作，称为反转，它可以旋转缠结，并将所有的过交点改变为过交点的下交点，反之亦然:

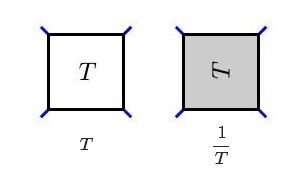
按照与上面所演示类似的思路，康威证明了每一个缠结的$T$都可以写成连分式的形式:

$$T \sim \left[ a _ { 1 } \right] + \frac { 1 } { \left[ a _ { 2 } \right] + \ldots \frac { 1 } { \left[ a _ { n - 1 } \right] + \frac { 1 } { \left[ a _ { n } \right] } } }$$

那么与缠结$T$相关的有理数就是$f ( T ) = a _ { 1 } + \frac { 1 } { a _ { 2 } + \ldots \frac { 1 } { a _ { n - 1 } + \frac { 1 } { a _ { n } } } }$。

康威随后利用这种缠结的描述，通过将它们分解成缠结序列，发展出一种缠结符号。通过这种方式，他能够创建一个包含11个或更少交叉点的所有结的列表。这个列表扩展并修正于19世纪晚期Tait，Little和$Kirkman$的作品。康威用了6年的时间来整理他的作品，他利用了一个下午，系统的描述了他的作品。

有趣的是，开尔文试图将这些化学元素描述为打结的涡线，而对绳结的研究正是源于此。用这种方法，他希望能解释这些元素的某些化学性质，因为这些性质是由结引起的。虽然这种方法最终被抛弃了，但泰特还是受到启发开始对绳结研究，这反过来又导致了绳结在数学上的理论。

大约经过100年的数学研究，这些思想在现代DNA研究中得到了应用。Sumners对这个问题提供了一定的描述:如果一个细胞的细胞核有一个篮球那么大，那么$DNA$分子的大小大概相当于一条长达200公里的钓鱼线的大小。酶的作用促进了重组过程，使分子的一条链穿过另一条链。结的数学研究也描述这个过程，并且提供了有用的工具。特别是，Goldman和Kauffman展示了我们在这篇文章中看到的一些想法是如何以这种方式使用的。

康威的广场舞是以活动为基础的项目，比如说，可以和中学生一起组织。希望本文有助于研究文献和对老师对这一活动描述之间上的差距。

参考文献

1. John Conway. An Enumeration of Knots and Links，and Some of Their Algebraic Properties. Computational Problems in Abstract Algebra. Oxford，329-358. 1970.

2. John Conway. Tangles，Bangles and Knots with John Conway. UC Berkeley Graduate Lectures. 2014

3. Louis Kauffman and Sofia Lambropoulou. Classifying and Applying Rational Knots and Rational Tangles，Contemporary Mathematics 304，223-259. 2002.

4. Jay Goldman and Louis Kauffman. Rational Tangles，Advances in Applied Mathematics 18，300-332. 1997.

5. Tom Davis. Conway's Rational Tangles.

6. Davis gives some ideas for using Conway's square dance with a group of middle or high school students.

7. DeWitt Sumners. Using Topology to Probe the Hidden Action of Enzymes. Notices of the American Mathematical Society 42 (5)，528-537. 1995.

8. C. Ernst and D.W. Sumners. A calculus for rational tangles: Applications to DNA recombination，Mathematical Proceedings of the Cambridge Philosophical Society 108，489-515. 1990.

原文链接:	http://www.ams.org/publicoutreach/feature-column/fc-2017-08
作者:	David Austin，Grand Valley State University
翻译:	程晓亮，吉林师范大学数学学院副教授
	邬昊然，吉林师范大学基础数学专业研究生二年级