如何驯服不确定性

善科文库团队 2018-11-28 3073

Marianne Freiberger/文
程晓亮迟明月/译

你会让数学模型决定你的生命吗?如果你还记得2008年的金融危机，那么你的答案很可能是不。大多数人将这场金融危机归咎于错误的数学模型预测。

事实上，你每天都要多次使用数学模型。无论是你上班所开的车，还是路上经过的桥，你使用的许多工具和设施也都是借助于数学模型设计的——包括用数学模型评估它们的安全性。

数学模型预测具有不确定性，不管我们有没有意识到这一点，不确定性在我们生活中都扮演着重要的角色。那么数学模型是如何起作用的呢？

1.什么是模型？

为了找到答案，我们首先需要了解什么是数学模型。它既不是一个物理对象，也不是一个特别简洁的公式，而是由一组方程（通常物理方程）组成：例如描述天气变化、或机翼周围气流的方程。Plus杂志上有很多关于数学模型的文章，非常简单的例子，想象在地上滚动的球。第一个力可以用牛顿第二运动定律描述：$f = ma$，即力等于球的质量乘以其加速度。

我们可以用模型模拟过程，也可以预测过程:例如明天的天气，在不同条件下机翼的性能，或者球的速度。数学模型除了帮助我们展望未来，还能帮助我们测试设计的产品，并且不需要进行实际地构建、碰撞、加热或者任何可能与产品实用性、安全性相关的操作。

在金融部门、制造业、天气预报中，数学模型只在幕后为我们提供信息，曼彻斯特大学的凯瑟琳·鲍威尔说，如果我们没有模型，我们的生活会大不相同。鲍威尔是剑桥艾萨克牛顿研究所不确定性量化项目的组织者。

1.1模型的不确定性

数学建模的第一步是写出：我们认为最能描述过程的方程。鲍威尔说：我们会利用所有知识写出方程，包括任何可使用的数据。没有一个数学模型是精确的，但每个数学模型都近似真实世界。从真理到模型总是存在误差。例如，上面的球模型不能描述现实，因为它忽略了摩擦力。

数学建模不确定性的第一个来源：即使我们尽自己最大努力完成数学建模，我们也无法准确用数学模型描述现实。数学建模中最常见的错误是选择不合适的模型，然后将其与现实混淆。这种错误在一定程度上导致了2008年的金融危机。

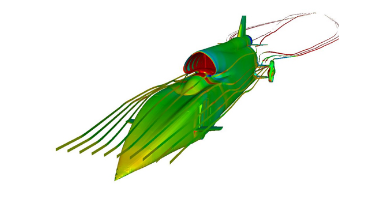
图为猎犬号超级汽车周围气流，以及汽车周围的压力轮廓和流线型

1.2近似不确定性

一旦我们写出方程，我们需要在预测中解释它。如果我们知道球的加速度$a = \frac{f}{m}$，那么球的质量决定力（忽略摩擦）。不过，这并不容易。鲍威尔解释说：大多数复杂模型都是非常繁琐的，并且简单的计算无法求解，例如模拟天气或气候变化的模型。所以我们要进行研究，看数学模型是否可以使用近似解，这称为数值方法。

数学建模不确定性的第二个来源：任何近似数都伴随误差。这就是数值分析领域的工作，鲍威尔说。在不知道问题的真正解之前，我们要陈述数值计算的相关误差。

1.3输入不确定性

到目前为止，我们忽略一个小问题：模型输入。在上面的例子中，如果我们要预测球的加速度，我们需要知道球的初始滚动力和球的质量。如果我们要预测明天天气，我们需要知道今天的天气状况，例如今天温度和压力。如果我们的模型是描述随空间变化的过程，比如容器内部温度变化，那么我们还需要边界条件：容器本身温度。

在实际情况中，我们很难获得模型输入值。例如，在工程问题中，我们不知道输入值，鲍威尔说。我们可能有猜测数据，但这些猜测数据通常不确定。例如，模拟指定地点的地下水流动，重要的输入参数是：研究区域岩石的渗透性。我们通常只能钻孔测量岩石渗透率。但钻孔成本非常高，所以我们只能通过测量来推断整个区域的渗透率。

数学建模不确定性的第三个来源：我们不能确定模型的所有输入值。著名的蝴蝶效应可以将这种不确定性夸大到无限。输入值中一个小错误会像滚雪球般越滚越大，以至于模型预测与现实相差很大。这也是天气预报的主要问题。

现在，我们已经确定数学建模不确定性的三个主要来源：模型不确定性、输入不确定性和近似不确定性。现在的问题是如何驯服不确定性。这就是我们接下来研究的内容。

如果在这篇文章的第一部分中，我们能确定数学建模不确定性的主要来源。接下来，我们来研究如何驯服这种不确定性。

2.掌握不确定性

鲍威尔说:[驯服不确定性]是很困难的，通常我们应该做什么，没有一个普遍的共识。就模型误差而言，我们所能做的就是测试模型，看看模型如何和现实相匹配，并不断地用数据验证模型。例如，在气候科学中，模型通常从过去的某个时间点开始使用气候条件，然后预测今天的天气。如果他们预测的很好（目前气候模型也做得很好），那么他们未来可能做出准确预测。

当模型涉及近似值误差时，模型就会发生数学变化。鲍威尔说:数值分析师通常从复杂模型开始，然后分析计算误差，这种算法可以求近似解。为了得到误差的相关结论，我们可以利用方程结构信息做出假设（关于输入和输出）。我们知道如何做简单模型，但不知道如何做复杂模型。

全球变暖预测

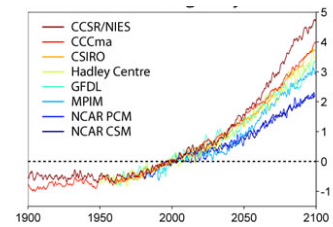
图为世界各地气候中心对未来温度的预测，这些预测
不完全相同，因为模型对二氧化碳和其他因素作出不
同假设，但他们都预测到二十一世纪末温度会显著上升

2.1前进

数学建模不确定性的第三个来源，输入不确定性，我们通常使用专门设计系统处理数学领域概率：概率论。如果我们不确定某个特定数值，我们可以使用概率，给它取可能值。例如，如果我们不知道上面例子球的质量，那么我们可以在400克和500克之间选择一个数，在这个范围内每个质量值都可能正确。在这种情况下，我们说球的质量是均匀分布的随机变量。

将质量的随机变量代入方程中，我们知道球的加速度还在一个具体的范围内（这取决于质量范围和力的大小），在这个范围内加速度取任何值的可能性相等。

这是未来驯服不确定性的基本概念，鲍威尔说。

已知输入值的概率分布，我们如何在模型中计算它，然后在概率分布的基础下估计解？我们得到的信息并不准确，但这些信息仍然可以回答重要问题。鲍威尔说:例如，我们可能知道发动机内部温度什么时候达到临界值，这对发动机来说是非常不利的。我们知道更改参数会对模型预测产生影响。

在复杂模型中，驯服不确定性是非常困难的。选择概率分布很棘手——理想情况下，在数据基础上选择概率分布，如果我们没有太多数据，我们就依赖专家意见进行选择。如果我们只对输入参数进行间接测量，那么问题就会更加复杂。在地下水的例子中，苏塞克斯大学的Masoumeh Dashti解释说:我们可能没有测量岩石的渗透性，但我们可能测量（地下水）压力。通过测量水压推断岩石渗透性，类似地，仅从物体影子推断物体形状——这是逆问题。概率论的研究者可能想知道，如何使用复杂的数学方法解逆问题。目前贝叶斯定理是热门研究课题。Dashti也正在研究此课题。

图为伊莎贝尔飓风，在2003年，它摧毁了美国部分地区

2.2计算能力

一旦我们有输入参数的概率分布，我们需要通过模型计算它，并得到输出数据。但有一个主要问题：大量的计算。

不确定性输入对模型输出可以隐喻为从帽子中抽取输入的特定值，然后用该特定值运行模型以得到答案。这样做很多次，就会得到输入参数的概率分布，但要确保在帽子中随机选择。这将给出大量的输出数据，这些输出数据反映了解的统计特性。

复杂模型面临的挑战是，模型运行需要很长时间。例如，对于制造、工程、物理应用的复杂模型，每次模型运行时，我们都在谈论运行时间。模型需要运行很多次，也许几百万次，然后计算输出的平均值。如果我们不使用这种采样方法，而是通过模型提供输入参数分布，那么模型将变得更加复杂，并且需要大量的计算。无论我们选择那种方法都会存在问题。

要使我们上面提到的方法更简单，我们需要付出更多努力。具有讽刺意味的是，这种方法涉及很多近似值，之后会引入更多的误差。

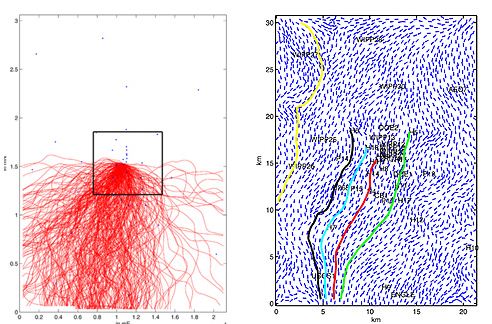
图为300个不同渗透率的岩石释放到地下水流的模拟路径，右图为标记颜色的粒子释放到不同平均值流场

2.3那么我们应该相信模型吗？

显然，从驯服不确定性的表面看，我们很难相信模型。那么我们为什么要相信复杂模型预测，比如天气预报？

鲍威尔说：外行人很难相信建模，尤其当我们说模型不正确，或者数值计算有误差，等等。鲍威尔和达什蒂认为，这归因于不良的交流和教育。鲍威尔说：在我们成长过程中，我们没有学到很多关于不确定性的知识；人们普遍认为，不确定性是无法解决的。作为数学家，我们不知道如何和人们更好地沟通。我们需要与更多了解道德和哲学方面的人交流。我们还需要推广更多成功数学建模案例。

就模型本身而言，我们应该记住建模是关于预测的，而预测的本质是不确定的。成功的数学模型是建立在科学和现有数据基础之上，并不断地与现实作对照。数学家鲍威尔和达什蒂能想出他们的预测结果。即使模型制造和使用模型过程存在错误，但没有人会选择模糊不清、毫无意义的模型。