在配置有GPS功能的智能手机普及之前的日子，我们要用到地图来导航。地图通常都是很大的一张平纸，而且非常有用。麻烦的是当我们完成查图之后要把它折叠回去。把地图重新折好的方法从来都不是一件显然的事情。即便地图已经被提前折好、折痕是非常简单的网格类型。为了将地图折回长方形以放回你的口袋，你需要很仔细的沿着直线一片一片的折好。这件事看起来连白痴都可以做好，但是你常常在向前折还是向后折的时候做反了，从而地图变得扭曲而你开始咒骂并一次、一次、又一次地尝试直到感到烦躁把地图丢到汽车座椅下面不了了之。

传统的导航方式

数学家们也有同样的烦恼。从来没有人找出计算任意多少网格的地图有多少种不同折叠方法的公式。这个问题困扰了几代研究人员。人们现在还在写相关方面的论文。

然而最近一个数学的本科学生的直觉建议这个问题或许有其它解决办法，这种方法在组合学、涂色问题和折纸之间建立起看似不可思议的联系。

Tom Hull 是位于马萨诸塞州春田市的西新英格兰大学的一名数学家，他曾经研究过三浦折纸问题，这是一个经典地图折叠问题的变形。相对于垂直的网格折叠，三浦折叠是在相交角度为84/96的网格上折叠。它看起来如下

三浦折叠。图片由MetaNest 提供。

三浦折叠法是由日本天文物理学家三浦公亮发明的，他和其他人一样在地图折叠问题上感到受挫。除了让袋装地图变得更方便，三浦折叠法还能够让卫星安全的收起和展开它们的太阳能板。

让我数一下有多少种方法

三浦折叠的天才之处在于它能非常简单的每次都用同样的方式打开、折上，仅仅需要将对角的两个角一推或者一拉。但这不是唯一的可行的折叠方法，只是其中最简单的一种。还有许多其他种折叠的方式。不同折叠方式的数目几乎与通常的90度折纸法差不多，在90度折纸法种，每个顶点可以有8种不同的折叠方式。三浦地图在一个顶点处只有6种不同的折纸方式。Hull认为三浦折叠法由于具有一定的几何约束会使得计算所有折叠方式的数目这一问题变得更加容易处理。

他把这一挑战交给一个本科学生Jessica Ginepro。最开始的时候，他们两人希望找到计算带有N个横折线和M个竖折线的三浦折叠的一个一般性公式。但很快他们就意识到这根本就办不到。$1\times N$的地图的所有可能折叠方式的数目由下面公式给出 $$2\times 3^N$$ 对于$2\times N$地图，这个公式是 $$(\dfrac{34+8\sqrt{17}}{17})(\dfrac{5+\sqrt{17}}{2})^N+(\dfrac{34-8\sqrt{17}}{17})(\dfrac{5-\sqrt{17}}{2})^N$$ 对于$3\times N$的情况，公式就需要写满一张纸了。

“这很讨厌。真的、真的令人讨厌”， Hull说道。Ginepro 仍然在尝试找到$4\times N$网格的公式。但是她发现或许有不同的方法去做这个问题。一天在试着玩的时候，Ginepro把$1\times N$的公式输入到整数序列在线百科。她惊奇的发现百科给出了一个匹配。这些数字与一个看起来无关的涂色问题所产生的数字完全相同。

这真是奇妙的意外。涂色问题代表着约束一类问题的挑战。一个经典的例子是在一张地图上涂色使得相同颜色的国家没有共同的国界。另外一个例子是数独，数独中每个格子中的数字被周围格子的数字所约束。商业实体中，如货物航运和航空公司一直都在处理约束问题，他们希望有一个框架和解决问题的更好的方法。但是没有人想到涂色问题会和折叠问题联系在一起。

Hull 和 Ginepro还没有找到一个将三浦折叠转化为涂色问题的简单方法，对于推广到其他折叠法的方法就知之更少。但是为了有一个如何将涂色和折纸联系在一起的具体想法，我们考虑一个可以在平面上折叠的图形，例如下面这个纸鹤：

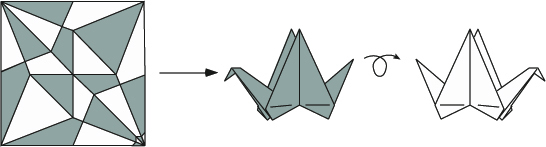
假如你想给这个纸鹤涂色使得有共同边界的区域涂上不同的颜色，你只需要2种颜色就可以了。当你将这个纸鹤折起来的时候，所有相同颜色区域都会面向同一个方向，所有图了另一个颜色区域都会面向另外一个方向。

大多数涂色问题都很抽象，但是和涂色问题的这种联系给折纸问题提供了一个有希望的解决方法。

倒扣

这并非事情的全部。折叠问题也与统计力学有关联，统计力学从概率论的观点研究各种材料的行为。有物理学家和Hull及Ginepro合作研究折叠问题的统计力学。他们并不是十分关心找到将一个地图、折叠锥体或者其他折纸折起来的所有方法，他们想知道如何正确地折叠。或更确切地说，将正确的折叠法变成最可能的折法。“数学并不关心这个问题，但是物理学家们确非常在意”，Hull说道。

物理学家之所以关心这个问题是因为他们正试图用成片的聚合物造出可以自组装的物体。当聚合物膨胀的时候（这通常是由于潮湿或者酸碱度的改变引起的），它们就弯曲并折叠起来。研究人员可以控制弯曲和折叠的轮廓，但却不能控制它们到底是折成山峰还是谷底。这是关键。折叠成一个山峰还是谷底取决于它形成的时候材料内部的应力。这些应力可以由统计力学进行描述，但这是一个非线性问题。在20世纪的时候，非线性问题还并不流行，大多数研究人员将弯曲和折叠问题当成废物。但是近期的工作显示出我们的肠道、大脑和其它组织是在它们的材料性质的控制下自组装成为可以预测的折叠形状的。植物的叶子和撕裂的塑料袋似乎也遵循同样的法则。进化已经能掌握折纸工程，为什么我们不能？

如果山峰和谷底不能正确的折起来，这个折叠锥仅仅是一张起皱的纸而已。

现在有三种方法将涂色、折叠和统计力学等问题建立起数学关联，这些方法或许会有用。第一种，它或许使得我们可以理解为什么结构会出现我们并不希望的形状。第二种，它或许能让我们找出重要的折叠方法。或许在所有的折叠法中存在某些方法，如果我们采用这些正确的方法去折就会使得物体本身正确的自组装起来。第三种，或许会让我们制造出有两种方式的折纸形状，我们可以在向前或向后之间转换从而形成山峰或谷底，Christian Santangelo说道，他是麻省大学阿默斯特分校的一位物理学家，现正在这一研究项目上进行合作研究。

将地图折起来并不简单。

从折叠问题到涂色问题再到软材料的工程的统计力学是一个缓慢的飞跃。但是最伟大的研究进展经常出现在最看似不可能的地方。“真正的希望是如果涂色问题被证实与折纸有关联，Tom [Hull] 就能以此说一些有关折纸的很酷的事情”Santangelo说道。

Kim Krieger 是一名来自康涅狄格州 Norwalk 市的自由撰稿人。她涵括了华盛顿的科技政策、纽约商品交易所的大宗商品价格以及各处的数学发明。