编者按：张寿武，安徽人，1979年考入中山大学化学系，后转入数学系，1983年毕业。之后在中科院研究所攻读硕士学位，师从数学家王元。1986年毕业后赴美国哥伦比亚大学，师从著名数学家吕西安·施皮罗(Lucien Szpiro)与格尔德·法尔廷斯(Gerd Faltings)，1991年获博士学位。此后任职普林斯顿、哥伦比亚大学。1996年任哥伦比亚大学教授，同年证明世界性难题波戈莫洛夫猜想(Bogomolov conjecture)；1997年在世界上率先于全实域上推广了格罗斯---乍基亚公式。2011年起任普林斯顿大学教授，美国文理科学院院士。

今天非常荣幸来到清华大学。我也是诚惶诚恐，因为清华是现代科学和数学的摇篮。所以，今天的华罗庚讲座对我而言也是意义比较大的。华先生从江苏金坛走出来，只有中学的训练水平，能够进入清华大学，到图书馆工作，最后变成清华大学的教授。解放后可以说是中国数学界最伟大的开拓者。我们很难想象如果没有华先生，我们中国的数学会现在是什么样子。肖杰和我这些人，在那样艰苦的条件下，依然能够在中学的时候，读到华先生写的很多书。那时候，资料非常贫乏，华先生的书对于我们这些60后能够在今天做出一点成绩是绝对分不开的。我今天的报告，要从华先生的老师的老师开始。华先生的老师是杨武之先生，当然是熊庆来把华先生接到清华，但真正接触到数论还是靠杨武之先生。

杨武之是杨振宁先生的爸爸，也是中国第一个数论和代数方面的博士。杨武之先生的老师是Dickson (编者注：Leonard Dickson)，Dickson是美国第一位代数和数论的博士，他在哥廷根念的学位。Dickson回到美国之后，在Chicago培养了一批数学家，包括杨武之。Dickson在美国和华先生的情况很接近，也是一枝独秀。他花了很多时间来研究西方的数学史。他写了三卷书，叫做History of the theory of numbers，我的报告从他的书里面的一段话开始写起。这是我百分百把他的那段话翻译成中文，他在第二卷某一章写了这样一个问题，在公元972年或者更前，一个不知名的阿拉伯的手稿留下了这样的问题：

给一个整数$n$，求一个平方数$\gamma^2$，使得$\gamma^2 \pm n$都是平方数。

从这个问题的叙述方式，发现它和三角形没有关系。有理由相信阿拉伯人提出这个问题的时候没有受到古希腊数学家的影响，这个问题在Dickson的书的第二卷可以找得到(Page 462)。这样的n称之为同余数，这里很多搞过奥数的同学知道同余是什么意思，但这里的同余不是这个意思。这样的同余更多的是和谐的意思，这样的数很少，因为是平方数的等差序列。24是同余数。这是因为：

从而6也是同余数，所以，考虑同余数，只要考虑没有平方因子的数即可。那问题来了，为什么从6开始，1,2,3,5是不是同余数？

下面直接跳到500年以后了，是1220年，斐波那契的年代。斐波那契差不多是中世纪最聪明的数学家。他生活在意大利的比萨，大家都知道那里有一个斜塔，伽利略在那个地方把球给丢下去了。那个城市有两位名人，一个就是斐波那契，一个就是伽利略。比萨那边有个高等师范学院，是拿破伦占领意大利之后建的。学院旁边的铜像是斐波那契的。斐波那契的“波那契”是他爸爸的名字，斐波那契基本是他爸爸的儿子的意思（笑），所以这个名字没有多少意义。斐波那契在当地是个非常有名的数学家，所以有一天国王的御前学者们——胥嗚伟老师替我翻译的，翻译得很准，向他挑战——找到一个有理数平方的等差数列，其公差为5，即

看看小朋友们能不能算出来？~~斐波那契证明了5和7都是同余数，你们有小学生证出来的我给你100块钱（笑），有没有小学生能算出来？或者中学生也行~~中学生不行我就推到大学生了。（人大附中某学生：5应该可以，29+20是7的平方，29减20是3的平方）啊，不错，一会记得向我要钱。。。啊？哦，不对，你算错了，你应该倒贴我100块钱（笑）。没办法是吧，再给你30秒钟时间，看看你是不是比斐波那契更聪明一些。大学生有没有会的？研究生的？清华的学生会吗？你现在不会的原因是你没有找到计算它的办法，到了讲座的中间你会发现计算同余数的秘方。好了，我们来看一下：

这个显然有点困难了吧。短时间内要算到分子分母100以内，如果都能算完，说明你脑袋特别快。要算7就更了不得了。当斐波那契算完7之后，他猜想1,2,3都不是同余数，但不会证明。

他的猜想，又过了400年之后，由杰出的数学家费马证明了。费马用的方法叫无穷下降法。下面到了所谓的秘方，同余数的问题一般叙述为，找一个面积为n的有理三角形。10世纪的时候，这个问题被认为是有理三角形理论的一个主要课题。为什么呢，因为，今天我们学的几何和代数是源自2300年前欧几里得的《几何原本》。虽然无理数很早就被发现了，但是大家关心的还是有理的对象。有理三角形问题无非研究有理面积和三个有理边长。所以被认为是主要问题。通分之后，从而可考虑三边都是整数，当然，n不再是无平方因子了。

下面我来解释一下从同余数的原来形式到三角形的形式的转换过程，如果事先有

那么令

从三角形到原文也是容易的，给定直角三角形边长a，b，c，令

则有

满足要求。所以现在有了更好的方式来理解同余数。我想说，这个问题还没有被解决。对于5,6,7这三个同余数，5,7的表达式比6复杂很多，所以它们虽然很接近，却很难发现。

费马是历史上非常伟大的数学家，精确的说是最伟大的业余数学家。但他的成就即使和专业数学家相比也是排在最前面的。他是普鲁斯的一个法官，由于法官的因素，他不能和普通人在一起，他要回避跟公众亲密的接触。所以他的生活比较孤独，一孤独就喜欢做数学（笑），所以他就花了很多时间研究数学。他研究数学，但是他不喜欢把过程写下来。他做出来以后，就寄给他的朋友，所以他几乎所有的数学都是在信件中。他一旦发现他证出了一个定理，他非常激动，告诉好朋友，“我找到一个极其妙的证明”（笑）~~然后大概描述他是怎么证的。有时候他还要向其他人去挑战。费马生活在牛顿之前，在数学史的贡献是极大的。数学在欧几里得和费马之间几乎是个空白，费马基本是是徒手引入了近代数学的一些概念。我们现在微积分的求切向量，求斜率，求面积，甚至有一些变分法。要知道变分法是无穷维空间的微积分，但是即使这样，费马也做了。费马肯定有了坐标的想法而且他用了。费马和笛卡尔是同一个时代的人，他们是一辈子的对手（笑），相互都不喜欢对方，但是，从来没有见过面。笛卡尔是个很严肃的数学家，也是个哲学家，他当然不能容忍费马那样信口开河“这是对的”“这是错的”（笑）。牛顿写微积分的时候，谈到他的关于微积分的工作是费马的工作的延续。回到这个最聪明的办法，无穷递降法。这个最聪明的办法只能证明否定性的结果。“不存在整数直角三角形，它的面积是平方数”，这是他的信里面写的很明确的一件事情。他是怎么证的呢？如果存在这样的三角形，则存在另一个整数直角三角形，它的面积也是一个平法数，且它比刚才那个三角形要更小一点。一直下去是不可能的；因为面积是整数，不能越来越小。他说他的的论述非常长，没有办法在信里面。我要引用的是20世纪最伟大的数学家之一Andrew Weil(韦伊)，他也有很多故事，他是Bouraki(布尔巴基)的精神领袖。Weil写道“所幸，书页有一处空白，可以让费马写下他的想法。大家都知道费马最后定理，（翻译成费马大定理是错的），就是他写了这句话，让大家花了300年的时间才证明出来。费马怎样证明1不是同余数呢？从欧几里得的《原本》，element，更精确地翻译叫《元素》，因为element在古希腊意思不是princeple，而是组成的基本元素。就好比汉字的笔画，英文的字母一样，这是最基本的。这个书里面最高成就是我们中国人所谓的勾股定理，中国古代也有很多辉煌的数学成就，只不过秦始皇焚书坑儒，所以，我们不知道我们是否有更大贡献。当然，除了勾股定理，欧几里得还有著名的辗转相除法——给出两个数，如何求公因子。从而，可以得到一个整数可以分解为素数的成绩。我们从小学到初中学的只是欧几里得著作的一部分。你可以想想，全世界，各种地区，各种文化，这些中小学生都在念这本书；我想，这本书一定是所有教科书使用率最高的。我们可以把三边互素的直角三角形的三边用很简单的公式表示出来：

这个公式告诉你怎么找整的直角三角形。基本是所有学初等数论的学生都要证明的第一个定理。我想说的是，这个公式，2300年前，欧几里得已经知道了。现在可以告诉你同余数的秘方了：

要记得要把平方消掉。现在再来算算？（对刚才算错的学生说：你要是算对了，一百块钱就不扣了~~）技巧就是要保证，p，q大多数都是平方，否则你消不掉啊？对于5，取一个5，一个4，对不对？恭喜你，答对了！6是最简单的。7呢？取25和7是吗？啊，对的，不过，存在更小的p，q，16和9。那个国王的御前学者们显然不知道这个公式。顺便提一下，斐波那契写了一本书，那本书第一次把阿拉伯数字引入了欧洲数学，以前欧洲还是用罗马数字。

现在来看看费马是如何证明1不是同余数的。否则，有个有理三角形，面积为平方。对应的p，q均为平方。从而上式的四个因子均为平方。令

从而

故存在r，s，使得

因此得到了边长为

的直角三角形，其面积

比原先的三角形更小。从而可使用无穷递降法。那么，这个并不难的证明为什么费马之前无人做到，用现在的话来说是心态问题，数学归纳法是往上走，但费马往下走。这就是费马非常得意的地方。这个方法是数学归纳法的变形方式。但是，在心理上是个更大的挑战。要用费马无穷递降法，首先要给出一个度量，比如面积。

下面考虑的是至今仍不知道的。我们看看同余数的分布问题，设n是个无平方因子的正整数。

猜想 我们有

就是说，随便给个数，比如99，模8余3，那实在没时间算的话，那你就猜他不是同余数；有时间就算一下。实际上，对于猜想后部分，用随机矩阵理论还可以猜得更精细，这里我不想细讲了。大家看看23以内的同余数吧。（把同余数写在黑板上），如果大家能把对应三角形的边长写出来，我就给大家钱，嗯，我把价钱写下来~~（笑）。对了，不能用电脑哦，必须用手算。你已经做出来了？哦，记得找我要钱啊。此外，领钱，年龄小优先啊~~有两个例外，34和41，这两个算出来，我给你200块钱。啊，还有219。对了，你要造出2个三角形。怪现象是如果模8余1,2,3的话恰好是同余数，那么恰好有两个本质不一样的解，它跟一般的不一样。219也是一样。

回过头来，我考虑同余素数问题。刚才的公式，一个很大的问题是，即使很小的n，也可能需要很大的p，q来对应。有这样的定理。

定理 如果素数P(分别地，2p)满足$p \equiv 3(mod8)$(分别地，$p \equiv 5(mod8)$)，则它不是同余数。

证明一个数是同余数比证明不是同余数难很多。数论学家发现更愿意做的事情是证明方程无解。我有时候和其他数学家交流困难，那些做方程的数学家，他们的方程一般有解。他们很困惑，为什么数论学家喜欢研究没解的东西。我说，不是因为我们喜欢没解的，而是不知道如何解方程。有解的这些定理在整个数论都是极其少见的。如果不是显然的解，我们一般不知道该怎么证。举个例子，157，模8余5，关于这个数是同余数的解非常复杂。

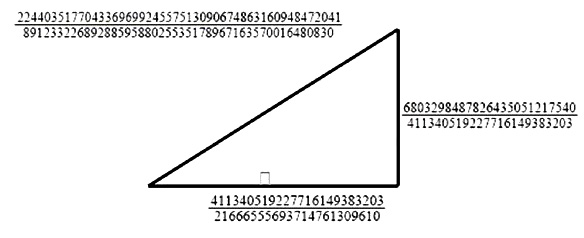
这可不是你在家里用计算器按一按就能捣鼓出来的。Heegner早就知道它是同余数。当然，算出来可完全不是这么简单。下午田野老师会告诉你怎么找出这个解。对于多个因子，其实也有很多定理。看看下面的定理，注意，“李德琅—田野”是两个人啊，不是个日本人的名字（笑）

定理 (冯克勤1996，李德琅-田野2000，赵春来2001)我们有存在无穷多个具有任意指定个数的奇数因子的非同余数。此外，存在无穷多个具有任意指定个数的奇数素数因子的同余数。

今天，很荣幸，李德琅老师和赵春来老师都来了，请站起来（掌声），从某种意义讲，今天的报告就是对这些人的贡献的总结吧。冯克勤老师原来是这个系的系主任。冯老师对中国发展代数数论做出重要贡献。我前几天和赵老师一同拜访了北京大学的前校长丁石孙先生，丁老师跟赵老师说的一些事情让我很感动。1983年，丁老师把“椭圆曲线的算术”引入中国，他跟赵老师说“你们这一代人肯定没戏了，你的学生可能有戏”。田野算是赵老师的学生，后来又和李老师合作。这张照片是田野老师在做报告，照片中报告的内容就是今天下午他要讲的（笑）。当然，要解决他们的工作，光用到欧几里得的东西是不够的。要用到椭圆曲线。

下面要给出同余数的第三种刻画方式。在椭圆曲线

找一个有理点（x，y），使得y非零。这个东西称为椭圆曲线，我想很多在高中念书的同学一定说我写错了。椭圆曲线不是二次的东西吗？你怎么出现3次方？其实我没有写错。椭圆和椭圆曲线是两回事。一个是椭圆曲线，一个是椭圆的曲线（笑）。当然，西方人的语文也不是那么差，这两者还是有联系的。椭圆和圆很接近，但是，学过微积分的同学都知道，椭圆的周长特别难求。虽然椭圆的面积很容易求，但是，周长算的话会出现根号带三次的东西。带平方总可以三角替换，但出现三次方就没戏。从而就有了新的函数，我们把它叫做椭圆函数。三角函数，我们知道正弦可以求余弦，因为余弦是正弦的导数。椭圆函数也一样，P函数和它的导数的关系就是三次，椭圆函数满足的方程叫椭圆曲线。我先简单解释下为啥和前面同余数的描述等价。

我现在要介绍椭圆曲线有啥妙的地方。这连丢番图都知道，丢番图是代数之父，他是公元后200年的人。他主要贡献是把欧几里得提到的算术问题拿出来重新研究，他研究了200多个方程，所以，大多数我们研究的方程他都知道。丢番图知道这样一件事情，三次方程有个很妙的性质，任何线和三次方程相交，有三个点。那你问有啥妙的。妙就在于如果你知道两个点，我就做一条线，交出第三个点，换句话说，我知道两个点，我就知道第三个点。还有更妙的，知道一个点，我做切线，得到第二个点。换句话说，给我一个解，我就能找出更多的解。这就是为什么你知道一个数是同余数，你可以造出无穷多个对应的有理三角形。这个丢番图已经知道，但是庞加莱知道更多。对于椭圆曲线的方程，一个大圈，一个小圈。对于三次表达式，某些区间是正的，某些区间是负的，如果是正的，就可以开平方，一正一负，这就是圈的来历。

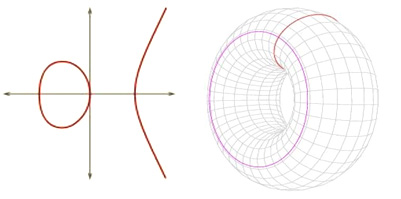
当然，如果你要考虑复点，就更有意思，这时候，解画不出来了，但是你要把复点粘起来，他是个车轮子。就是两个圆环乘起来。我在上面定义了一个运算，我想即使是丢番图也是有概念的——给定两个点P和Q，我就能交出S，再关于实轴反射，得到R,我得出P+Q=R,这是二次曲线所没有的。我就给你一条线，二次曲线就交出两个点，没了。所以，三次曲线比二次曲线有意思多了。你们高中没有学三次曲线是重大损失（笑）。

下面考虑椭圆曲线的有理点。下面是庞加莱1901年的猜想。

定理 (Mordell 1922) 我们有设$C/ \mathbf Q$是椭圆曲线，则存在r非负，使得

我关心的是，这么多有理点，有没有一些基本的？叫做生成元。我下面跳的比较快，不过，不用担心，我现在已经不再针对中学生了。也不是大学生，是给研究生讲了。当然，椭圆曲线对应的三次方程我没法解，但是，我可以先模2，模3去解。对每个素数p

考虑误差

之所以叫误差，即使模p的时候基本是50%的概率，基本是，50%有解，一旦有解就是两个解，正的和负的，所以基本上有p个解，因此这个基本上代表误差。实际上，可以证明

在此问题上，华罗庚先生也有贡献。把这些项乘到一起，得到所谓的L-函数：

L-函数讲起来很别扭，但是展开后就是p-级数判别法出现的级数类似的对象。这个级数当s的实部大于3/2收敛，当实部小于3/2的时候，它其实是有解析延拓的。这是Wiles证明的，这可以推Fermat大定理，大家都说Wiles证明了Fermat大定理，其实他证的是这个。现在要介绍100万奖金问题。这个问题是说，刚才那个函数在s=1处有Taylor展开：

猜想 (BSD猜想) 我们有$L(C,s)$在$s = 1$处的Taylor展开为

其中$c \neq 0,r = C(\mathbf Q)$的秩。特别地

这个猜想有什么意义呢？这个方程模p的解很容易求，从而L-函数理论上很容易构造。因此，判别n是不是同余数，只需把对应椭圆曲线的L-函数算一算就行了。

下午，田野教授告诉你该怎么算，他有个更快，更有效的方法判断哪些数是同余数。但是那个判别法要基于这样的猜想。如果你证了这个猜想，你拿了100万，还顺便证明了同余数问题。我记得丘先生说过，如果这个猜想被证明，肯定拿菲尔兹奖。当然，是顺带拿菲尔兹奖，清华也会发给你100万，那你至少200万入户了（笑）。当然，条件我忘了，北大的行不行，国外的行不行，不知道。

现在应用于同余数问题。考虑把s变到2-s，那么L-函数会变号，符号为

按照符号的正负，可以给出自然数集合的拆分

前者的符号为正，后者的符号为负。我们有如下猜想

猜想 我们有$n \in S$，则它是非同余数概率为1；$n \in T$，则一定为同余数(不是概率为1，注意)

这是目前对于非同余数唯一可行的办法。注意，100%是个很危险的概念。100个人的100%就是所有，但是，无穷多个人的100%就不一定是所有人了。

此外，猜想当n落入T时，100%的同余数均由Heegner点给出，这也是田野要讲的。

下面简单介绍一下Heegner这个人。知道费马的人横多，知道Heegner的人横少。当然，不知道他是因为他不是个职业数学家，他是个无线电专家，他在二战阶段有6个专利。他一辈子就写过两篇数学文章，第一篇是试图解决高斯类数1问题，这个问题是代数数论基本问题。高斯算出9个虚二次域其类数为1，且证明这样的数域最多10个，但不知道第十个是否存在。Heegner在做无线电的业余时间，就研究这个问题，这个文章证明了第十个不存在。这个文章他发表的时候已经59岁了，这是非常了不起的。可惜这个文章没有被整个数学界承认，直至多年后Stark和Baker给出新的证明。后来Siegel发现，Heegner的证明是对的，且是构造性证明。他52年发了这个文章，69年才被承认，这时他已经死了4年了。他的故事对我来说意义有两个，第一个是我现在也是50岁，看到Heegner老先生还能证明这么厉害的东西，很受鼓舞；另一点就是，如果你写的不好，死之前也没人承认。由于他不是职业数学家，所以他写的东西非常之难看，我们请胥老先生把这篇文章翻译过来了，有兴趣的话可以看看当年Heegner是怎么算的。我只介绍Heegner工作的要点。Heegner解决了类数1问题，顺带解决了同余数问题。只有到了Heegner，才具体证明了哪些数是同余数。

我们需要介绍模参数化，就类似于三角函数可以参数化单位圆一样。Heegner需要构造

的解的主要工具是模函数。这叫做双曲参数化。其实，椭圆函数的参数化对于解决这样的问题没有帮助，对做拓扑等其他东西有帮助，对数论没啥帮助。对于双曲度量，三角形内角和是小于180度的，所有的半圆都是测地线。用双曲几何给出这样的参数化，我没办法具体去理解双曲参数化妙的地方。我想通过一个例子，当然这时如果你有计算器更好，看看下面的表达式是什么东西：

事实上，算下来是这么个东西

田野告诉我怎么记，陈景润从国外回来，国家答应给他做人大代表，他就提议加了一辆公共汽车，就是320，我做学生时刚有320，终点到中关村；现在好像走的远一些了，以后让他们改回来（笑）。那么，大体上，模函数的特点和三角函数有很大相似之处。三角函数在2π的有理数倍取代数值，模函数在二次点上取代数值。什么叫二次点呢，下面会讲到，比如j（z）是个标准模函数

其中，$q=exp(2 \pi i)$，那么

就是个很漂亮的数。好吧，这是我最后一张胶片。好的，谢谢大家（掌声）。

（提问）

问：Heegner的方法用模函数解出参数方程和曲线的L-函数对应的模形式是否有关系？

张：当然是有关系的，不过Heegner他老先生不懂L函数。所以他愣是手算出来的，参数化都是手算出来的。

问：为什么要考虑椭圆曲线有理点？

张：因为有理点很好玩啊~~我在黑板上讲了半天很好玩，你觉得不好玩哈？（笑）。复点很简单。此外，还有100万奖金。

问：如果给一个整数，考虑有限域的三角形，可解，那是否对原方程可解？

张：你的问题就是如果局部可解，那是否整体可解？那不是，实际上，同余数基本都是局部可解。

问：Zagier算157的对应三角形的方法是否可以把您在黑板上写的几个秒杀了？还有，为啥考虑157？

张：当然了，你要算出来我给你一万块钱，一千块钱都少了点（笑）。为啥考虑157？因为157是素数，并且我们已经知道是同余数，当然我们希望把它具体算出来。

【感谢张寿武教授允许我们转载此文。汤涛教授校对并作了简单修改。】