什么是薛定谔方程
下面是一个典型的教科书问题：你的车已经用完了汽油，你要用多大的力才能把它加速到给定的速度？答案来自牛顿第二运动定律：
其中$a$是加速度，$F$是力，$m$是质量。这个完美、直截了当、但也细微的定律可以描述各种运动，因此至少在理论上可以回答一个物理学家可能要问的关于世界的几乎所有问题。
真是可以吗？当人们第一次开始考虑最小尺度的世界时，例如电子绕原子核旋转，慢慢意识到事情变得非常奇怪，事实上，牛顿定律不再适用。为了描述这个微小的世界，你需要用到迟至二十世纪初才开始发展的量子力学理论。这个理论的核心方程类似于经典力学中的牛顿第二定律，它被称为薛定谔方程。
薛定谔方程是以欧文·薛定谔（1887-1961）的名字命名的，。
波和粒子
“在经典力学中，我们使用位置和动量来描述一个物理系统的状态，”剑桥大学的理论物理学家NAZIM Bouatta解释道。例如，假设桌面上有一些运动着的台球，如果你知道了每个球在某个时刻$t$的位置和动量（即质量乘以速度），那么你就知道了该系统在时刻$t$的一切：这里的一切指的是运动的状态和运动得多快。我们会问：“如果我们知道一个系统的初始条件，即我们知道系统在时间$t_0$的状态，那么该系统的动态如何演变？牛顿第二定律可以帮助我们回答此类问题。在量子力学中，我们问了同样的问题，但得到的答复是棘手的，因为位置和动量不再是描述系统的合适变量。”
问题的关键是，量子力学试图描述的对象及其行为并不总是像小小的台球那么简单。有时，最好把它们看成是波。“把光作为例子，牛顿除了他关于引力的工作，也对光学有兴趣，”Bouatta说。“根据牛顿，光由粒子所描述，但是，经过许多科学家的工作，其中包括由詹姆斯·克拉克·麦克斯韦的理论所导致的认识，人们发现，光确实可用波来刻画。”
但在1905年，爱因斯坦认识到波动学说也并不完全正确。为了解释光电效应，你需要把光束视为被爱因斯坦称为光子的粒子流。光子数与光的强度成正比，每个光子的能量$E$与其频率$f$成正比：
这里$h=6.626068 \times 10^{-34}m^2 kg/s$是一个令人难以置信的小数，称为普朗克常数，以物理学家马克斯·普朗克的名字命名，他在1900年关于黑体辐射的工作中已经猜到这个公式。“因此，我们面临这样的情况：描述光的正确方法是它有时为波，有时为粒子，”Bouatta说。
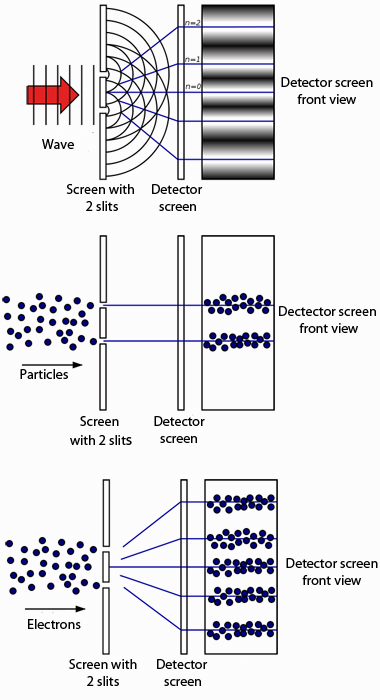双缝实验：最上面的图表示波经过双缝产生的干扰模式，中间是你期望看到的粒子发射通过双缝的图，底下那幅是实际粒子例如电子发射经过双缝的示意图：你得到期望的波干扰模式，但电子还是如同粒子的面貌达到。 爱因斯坦的结果可以与一个古老的努力联系在一起，它开始于17世纪的克里斯蒂安·惠更斯而在19世纪由威廉·汉密尔顿再次探索：将光的物理原理（这是关于波的）和力学（这是关于微粒的）统一起来。由于光自相矛盾行为的灵感刺激，年轻的法国物理学家路易·德布罗意在探索的征途中走出了戏剧性的一步：他设想不仅光而且物质受制于所谓的波粒二象性。物质的微小组成部分，例如电子，有时呈现粒子性，有时则呈现波动性。
德布罗意1920年代提出的思想并不基于实验的证据，而是由于爱因斯坦相对论所激起的理论考虑。但是实验依据将接踵而至。1920年代后期牵涉到晶体散射粒子的实验证实了电子的波动性。
波粒二象性的最著名演示之一是双孔实验。将电子（或像光子或中子那样的其他粒子）一次一个地对着有两个小孔的屏幕打靶。屏幕后面有另一张屏幕，它能检测通过小孔的电子在屏幕上的位置。如果电子具有粒子行为，那么它们在小孔后面的两条直线旁边堆积。但检测屏幕时人们实际看到的是干涉模式：这是电子具有波动性的图像，每个波经过双孔后在屏幕另一面后传播开时自我干涉。然而在检测屏幕上电子如同你所期待的那样以粒子的面貌到达。这确实是一个非常不可思议的结果，但它重复了无数次---我们必须接受世界就是这么运行的事实。
薛定谔方程
德布罗意提出的彻底新颖的图像需要新的物理。与粒子有关的波在数学上看像什么？爱因斯坦已经将光子的能量$E$与光的频率$f$联系在一起，后者又通过公式$\lambda = c/f$与光的波长有关，其中$c$为光速。运用相对论的结果，也可以将光子的能量与动量相联系。将所有这些结合起来就得到光子的波长$\lambda$和动量$p$之间的关系
其中$h$还是普朗克常数。
从这里继续走下去，德布罗意假设波长和动量的同样关系对任何粒子都成立。
这个时候我们最好不要管粒子行为（如波的说法）到底意味着什么样的直觉性，而就跟着数学走吧。
在经典力学里，波随着时间的演化，例如声波或水波，是由一个波动方程描述的。这是一个微分方程，其解是一个波函数，它给出波在任何时刻的形状（需要满足合适的边界条件）。
例如，设想你有一个直线波沿着$x$-轴方向的细绳传播开去，并在$xy$-平面内振动。为了完全地描述波，我们需要找到细绳上任一点$x$在任一时刻$t$沿着$y$-轴方向的位移$y(x, t)$。运用牛顿运动第二定律可以证明，$y(x, t)$服从下列波动方程
其中$v$为波的速度。
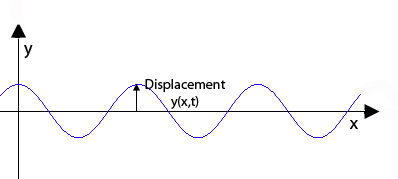在某一时刻的xy平面的线性振荡快照，这里呈现的波可以用余弦函数来描述。 这个方程的通解相当复杂，反映出细绳可具有各种方式扭动的事实，并且你需要更多的信息（初始条件和边界条件）来精确发现它所作的运动。但是，作为一个例子，函数
描绘了一个沿$x$-轴正方向移动并具有角频率$\omega$的波，因而如你可以期望到的，它是这个波动方程的一个可能解。
类似，应当有揭示神秘的“物质波”随时间演化规律的波动方程，无论它是什么。它的解应是一个波函数（但不要把它看成是刻画实际波的），它给出关于量子系统在任何时刻所知道的一切---例如单个粒子在某个空间内的运动。正是奥地利物理学家欧文·薛定谔在1926年找到了这个方程。对于在三维空间中运动的单个粒子，该方程可以被写成
这里，$V$是粒子的势能（它是$x, y, z, t$的一个函数），$i = \sqrt{-1}, m$是粒子的质量，$h$是普朗克常数。这个方程的解是波函数$\Psi(x, y, z, t)$。
有时人们需要求解仅依赖于空间变量的函数$\Psi$，即在某些情形下势函数不依赖于$t$。这时我们可以通过考虑较为简单的与时间无关的薛定谔方程：
其中$E$为粒子的总能量。整个方程的解$\Psi$则为
这些方程适用于在三维空间中运动的一个粒子，但也有相对应的方程描绘一个由多个粒子组成的系统。如果不把波函数写成位置和时间的函数，人们也可以将它们化为动量和时间的函数。
进入不确定性
我们可以用一些简单的例子来看看怎样求解薛定谔方程，并能知道方程的解的确类似于描绘波的数学方程的解。但是这个方程的解到底意味着什么？它并不给你粒子在时刻$t$的精确位置，因而它并不给你粒子随时间而行进的轨迹，而是一个函数，在时刻$t$给出对于所有可能位置$(x, y, z)$的一个值$\Psi(x, y, z, t)$。这个值意味着什么？1926年物理学家马克斯·波恩给出了一个概率的解释。他假设这个波函数的绝对值平方
给出在时刻$t$粒子位于位置$(x, y, z)$的一个概率密度。换言之，粒子在时刻$t$将在一个区域$R$中被发现的概率是
这个概率图像与德布罗意关于粒子波长和动量关系公式有令人吃惊的联系。维尔纳·海森堡1927年发现的一个结果是：如果要测量一个运动粒子的位置和动量，人们有一个基本的精度限制。在某一方面如果想要测量的精度越高，其他方面人们能说的就越少。这并不是指测量仪器的质量问题，而是自然界根本就具有的不确定性。这个结果现在称为海森堡的不确定性原理，且是常常用来引述量子力学奇怪现象的几个结果之一。它意味着在量子力学里我们谈论不了粒子的位置或轨道。
维尔纳·海森堡，1901-1976. 波函数是否有任何物理解释一直是个棘手的问题。“问题是，我们有这个波函数，但我们真的认为有随着空间和时间传播的波吗？”Bouatta说。“德布罗意、薛定谔和爱因斯坦试图想提供一个例如像光波在真空中传播的真实阐述，但是物理学家沃尔夫冈·泡利、维尔纳·海森伯及尼尔斯·玻尔都反对这个真实的图像。对他们而言，波函数只是计算概率的一个工具。”
它有效吗？
路易·德布罗意，1892-1987. 然而这个方程已经经受过到目前为止所有实验的考验。“它是量子力学最基本的方程，”Bouatta说。“它是我们想描述的每一个量子力学系统的出发点：电子、光子、中子，所有的。”该方程最早的成功，也是薛定谔的动因之一，在于描绘了帮助直接推动量子力学诞生的一种现象：氢原子的离散能量谱。根据欧内斯特·卢瑟福的原子模型，像氢原子这样的原子的放射线频率应当连续变化，但实验表明不是这样的：氢原子只放射出某些频率的射线，当频率变化时有跳跃。这个发现在常规知识面前飞走了，因为它支持了由十七世纪的哲学家和数学家戈特弗里德·莱布尼茨所指定的格言：“自然不允许跳跃”。
1913年尼尔斯·玻尔给出了新的原子模型，其中电子被限制在某些能量级上。薛定谔将他的方程用于氢原子，发现他的解精确地重现了玻尔制定的能量级。“这是一个令人惊奇的结果---是薛定谔方程的第一个主要成就之一”Bouatta指出。
由无数的成功实验支持，薛定谔方程已经成为牛顿第二定律在量子力学的类似物和替代品。
