生活中的很多事情使我们感到非常熟悉，以至于可能会忘记想知道它为什么会这样发生。性别比是一个很好的例子：男性和女性在世界上的数量是大致相等的，但是为什么会如此呢？

对于许多18世纪的思想家而言，答案在于天意---善良的上帝---每年出生的男孩和女孩的数量相等，是一夫一妻制的婚姻反映出的自然法则。这在查尔斯·达尔文的《物种起源》于1859年出版以及《人的后裔》1872年出版后开始改变，重点开始转移到寻找进化和自然选择的解释。达尔文做出了尝试，但很快就撤回，他得出结论：“整个问题非常复杂，把解决方案留给未来是比较安全的做法”。

该解决方案在20世纪到来。为什么大多数物种的雄性和雌性后代的数量大致相等的原因其实很简单，让我们看看如何可以用数学来证明一个直观的生物论据。

费舍尔原则

尽管人们不是很肯定英国遗传学家罗纳德·费舍尔是否真的第一个解释了进化有利于同等数量的儿女，但结果还是以他的名字命名：费舍尔原则。首先考虑二倍体物种，其中每个生物体的每条染色体有两个副本，一个来自母亲，一个来自父亲。这意味着，每一代的遗传物质一半来自母本，另一半来自父本。

假设在群体内，交配是随机的。这将意味着每个雄性和雌性的机体可以预期与相同性别的任何其他成员传递相同数量的遗传物质给下一代。在实践中，这可能不会发生，但它是一个有用的模型。现在考虑一种群体，其雄性比雌性多。男性传递的遗传物质的总量等于女性传递的总量，因为每个亲子得到两者等量的贡献。由于有更多的雄性，由此可见每个单独的雄性的期望份额将低于每个雌性，任何给定的雌性可以期望比任何给定的雄性传递更多的基因。

把每个父母视为一个投资者，希望给有限数量的子女获得最大的遗传回报。在以上考虑的群体中，很明显，对女儿有一个比儿子更好的“回报”，所以自然选择将有利于与雄性居多唱反调的生物，并产生更多的雌性后代。他们将有更多的孙辈，因此，偏向女性的性别比例将变得更加普遍，直到群体的雌雄数目相等。反过来，在雌性占多数的群体中，将有更多的儿子。相等的性别比因而是唯一的一个不能被不同的策略所击败的性别比，因此被认为是稳定的。

请注意，我们谈论的是一个稳定的策略，而不是一个最佳的策略。一个群体的最大可能增长与雌性数目成正比，因此，它的成员如果普遍采用了有点偏雌性的性别比的话，大概可以做得更好。但是，自然选择将有利于在群体中顶住这种趋势的个体，产生更多的儿子，因此这种策略不会是稳定的。有雌雄各半的子女未必是最佳的策略，但它是无与伦比的：没有与之竞争的任何策略可以做得更好，所以自然选择将有利于维持现状。

证明1:1是最好的策略

这些论据看起来相当有说服力，但数学上可以证明相等的投资是一个无与伦比的策略吗？让我们先来定义一些术语。

想象群体是黄蜂。其实任何物种都一样，但黄蜂是一个很好的例子，其一些变种的雌性有能力选择自己的后代的性别。假设每个雌性可以期望有n个子女，并用x表示这些子女中雄性的比例（所以$0 \leq x \leq 1$）。每一个雌性可以期望nx个儿子和(1-x)n个女儿。我们还假设，在群体内的交配是随机的。

为了证明费舍尔原则，我们需要建立一个不同生殖策略的适应度模型，然后证明没有办法击败1:1的比例。适应度是衡量一个生物体是如何成功地通过群体传播自己的基因，这里它的一个很好的定义是生物体后代生产自己小孩的成功程度。为了简单起见，假设有一个变种雌性，她可以采用任何性别比，并有一定数量的2p个雌性群组总是生产相同数量的儿子和女儿。

每个起始黄蜂的适应度是什么？用言语的答案是明确的：

请注意，这个答案和孙辈的数量是不一样的。假设完全随机交配包括兄弟姐妹之间的后代，所以女儿的后代和儿子的后代之间会有一些重叠。

让我们从变种黄蜂开始，并尝试以数字形式表达上述语言。把适应度用函数f(x)来代表。我们已经定义了女儿的期望数(1-x)n，因为每个女儿能期望有n个孩子，我们得到

儿子的数量也很简单---它的定义是nx---期望的后代数只是稍微复杂一些。请记住，我们假设群体内随机育种，所以（某个特定的一代）每个雄性的期望子女数等于（这一代）雌性的总数，乘以它们的子女的期望数，并除以（这一代）雄性的总数。我们可以分解如下：

我们可以通过我们得到的变种黄蜂的后代公式得到群组黄蜂的值，令$x=1/2$（由于性别比对分）再乘以群体内的群组黄蜂数量$2p$：

正如所期望的那样，对半的性别比意味着儿子和女儿的数量是相等的。把所有这些代入，给出

这是全面写出变种黄蜂适应度的公式所需要的一切：

也可写成

我们也需要群组黄蜂一个成员的适应度g(x)的公式。这个公式可以同法构造，但这时儿子的数量及女儿的数量均代之以$\dfrac{1}{2}$。其公式为

f(x)和g(x)都与$n^2$成正比。直观上这是合理的，因为一代的子女数与n成正比，因此两代的话就与$n^2$成正比。但是本质上我们不是真对后代的数目感兴趣，而仅仅是看变种黄蜂和群组黄蜂的期望适应度相互比较起来怎样，并且哪个更大。所以，我们去掉因子$n^2$，把公式写为

这些因子移去后，留下的公式与n无关。这表明一个生物体产生的后代数与稳定的性别比不相干：无论他们期望2个子女或2000个子女，都适用于同样的规则。

如果费舍尔原则是对的话，则群组策略不会被打败：F(x)绝不会比G(x)大。证明这点的最简单方法是定义一个新的函数，它是前两个函数的差：

它可简化成

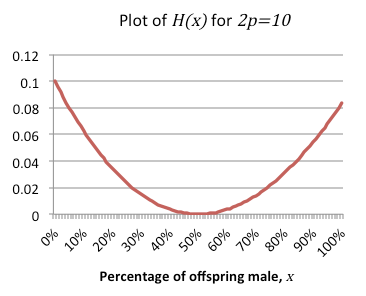
注意到H(x)的分母总是大于0，因为x不能小于0而p总是大于0。这意味着H(x)的符号由分子

的符号决定。故H(x)总是非负，仅在$x = \dfrac{1}{2}$处为0。

这恰是我们想要证明的：H(x)除零点$x = \dfrac{1}{2}$外处处为正。因此G总是大于F，除了当变种黄蜂和群组黄蜂采用同样的1:1的性别比，在这种情况下，两个函数的值相等。

用生物学的术语说，我们已经证明同等性别比不能被任何方式击败。

除了假设不对

不过，还不是完全如此。任何推导都仅仅和初始假设一样漂亮，但这里用到的几个假设也许有问题。

现在让我们只专注于一个假设：群体中的每个生物体都与其他生物体竞争。这可以是一个有用的模型，但在实际中显然不成立：南非Kruger国家公园里的狮子不会与伦敦动物园里的狮子竞争。在任何时刻，大部分生物体只与一般群体中的一个相对小部分的生物体竞争。

某些种类的黄蜂在这方面更为极端。在这些变种中，某些雌性在某个食物源处下卵，例如瘫痪毛毛虫，然后死去。当卵孵化后，新一代的黄蜂将吃饭长大，然后与来自同一食物源孵化的其他黄蜂不加选择地交配。雌性将离开住地，寻找新的住地产卵，而雄性则死光。

在这里，系统有两个值得注意的方面。第一个是不同性别比的局部适应度：在某个特定食物源，特定的性别比对不同黄蜂之间的竞争怎样有效。第二个是性别比的全局适应度：一个特殊策略与群体中所有黄蜂的平均成功相比较是怎样的。如果一种策略与群体中的平均行为相比更合适，则它将流行。

之前关于费舍尔原则的证明对于局部适应度依然有效：如果黄蜂采用了同样的性别比，那么它不会逊于在相同的食物源产卵的任何其他黄蜂。有趣的是，这并不能保证在全局级别上的成功，因为比局部竞争者做得好并不一定意味着比群体平均做的更好。

通过运用已经遇到过的类似想法，我们可以拿出一个适用于这种情况的广义模型。我们不会在这里开发这个模型，但只注意到它预测一个稳定的性别比：雄性$\dfrac{w-1}{2w}$对雌性$\dfrac{w+1}{2w}$，其中$w$是在一个地方产卵的黄蜂数量。当$w=2$时，一个无法击败的策略是后代小蜂的25%是雄性，$w=3$时为33%，$w=4$时变成37.5%，等等。

这个结果的两个有趣方面是它对非常小和非常大的$w$值所返回的答案。对于$w=1$，它告诉我们：儿子的比例为0是一个无法击败的性别比。这显然不是正确的，因为一字不差地说，它意味着在下一代将没有雄性，因而在之后的各代中也没有雄性。

在实践中它的意思是，当不存在与群体中其他成员的竞争时，最好的策略是产生尽可能少的雄性。此原则适用于某些种类的螨虫，它们下一代的孵化和繁殖是在自己母亲的身体中！没有来自其他物种的竞争可能性，这种安排产生的性别比大大偏向于生产女儿。

在另一个极端，$w$越高，性别比则越接近于理想的比例1:1。当有这么多生物直接竞争时，该模型变得与费舍尔原则的假定条件相接近，这时，一般的规则从一个特殊的情况中恢复而出。

这些理论预测可以与在自然界中观察到的性别比相比较，结果令人鼓舞。有许多因素使我们这里构造的理想模型复杂化，致使实际群体的性别比有这样或那样的小变化，但研究表明，最初倾向于雌性的性别比当黄蜂在每个地方的数量增长后趋向于1:1。这证实了应用数学的力量，只使用很少的一些合理假设和A-级别的技术，可以预测到一些可被实验证明的结果。