在布莱克-斯科尔斯方程中，字母代表这些变量：
σ=相关资产/商品的回报波动；S=当前价格；δ=变化率；V=金融衍生品价格；r=无风险利率；t=时间

这是投资人的圣杯。布莱克-斯科尔斯方程是费希尔·布莱克(Fischer Black)和麦伦·斯科尔斯(Myron Samuel Scholes)的发明，它给出了为还没完成的金融合同低价的理性依据。这就像是在比赛中对一匹马下注。它开创了复杂的投资新时代，催生了巨大的全球金融产业。但在次级贷款市场出问题的时候，可爱的金融市场变成了布莱克-赫尔（黑洞之音，与方程押韵）方程，把世上的钱源源不断的吸进去。

布莱克和斯科尔斯

注意危机发展的人都知道涉及商业和商品的实体经济与称为衍生工具的复杂金融工具比起来大为逊色。衍生工具不是钱或者商品，它们是对投资的投资，对预期的预期。衍生工具造成了世界经济的繁荣，但它们也带来了市场的动荡——信用紧缩，导致银行体系近于崩溃，经济暴跌。正是布莱克-斯科尔斯方程开创了衍生工具的时代。

方程本身不是问题。它很准确而有用，限制条件也交代得很清楚。它提供了用于评估金融衍生产品价值的行业标准。这样衍生产品就可以在到期之前进行交易。如果你合理地使用方程，在市场条件不合适的时候不要用它，结果很好。问题是有人可能滥用它。这个方程让金融衍生产品成了可以独立交易的商品。金融业把这个方程叫做“米达斯方程”【注】，认为它有把任何东西变成黄金的魔力。但市场忘了米达斯国王的故事的结局。

布莱克-斯科尔斯为大规模的几经增长奠定了基础。到2007年，国际金融系统每年交易金融衍生产品的价值有一千万亿（$10^{15}$)美元。考虑通货膨胀因素，这是上世纪世纪制造业产品总价值的十倍。缺点是发明的金融工具越来越复杂，它们的价值和风险也变得原来越不透明了。因而公司需要雇佣有数学天才的分析师来开发类似的方程，以判断这些新金融工具的价值和风险。但是，灾难是他们忘了问这些答案在市场条件发生变化的时候还能有多可靠。

布莱克和斯科尔斯在1973年发明了他们的方程，罗伯特·莫顿(Robert C. Merton)不久又给出了进一步的证明。这个方程对最简单最古老的衍生产品——期权是成立的。在此过程中有两类人参与交易。卖方期权给予购入者在特定时候以约定价格卖出一种货物的权利。买入期权与此相似，不过它指的是买入而非卖出的权利。方程提供了在期权到期前计算其价值的系统方法。这样期权就可以随时交易。这个方程非常有效，它帮助莫顿和斯科尔斯在1997年赢得了诺贝尔经济学奖（布莱克去世因而无缘诺奖）。

1997年诺贝尔经济学奖得主莫顿和斯科尔斯

如果双方都清楚衍生产品的确切价值，并且达成一致，怎么会有人能赚到钱呢？方程要求使用这估计若干的数量。不过通过衍生产品赚钱的关键是赢得你的预期——购入可以在将来高价卖出或者是到期后价值超出预期的衍生产品。获利者赚到的钱就是别人亏掉的。在任意年份，都有75%到90%的期权交易者亏损。在次贷泡沫破碎的时候，世界银行业损失数千亿美元。在随后的恐慌中，纳税人被迫买单。但这是政治，而不是数理经济学。

布莱克-斯科尔斯方程把期权的合理价格和另外四个量联系起来。其中三个可以直接测量：时间，与期权相关的资产价格以及无风险利率——这就是国债之类理论上没有风险的投资可以得到的收益。方程假定资产的波动在期权存续期间保持一致，这样就无需修正。波动可以通过对价格变化进行统计分析，不过它无法通过可靠方法精确测量，估值也可能与实际值不一致。

华尔街的智慧天才-布莱克

许多金融模型背后的思想源自路易·巴舍利耶(Louis Bachelier)在1900年的创制，他认为股票市场的波动可以通过一种称为布朗运动的随机过程来模拟。在任意瞬间，股价或张或跌，模型假定这些事件的发生概率。它们可能概率相当，也可能一个并另一个概率高。这就像是有人站在街上不停地丢硬币来决定是向前一小步还是向后一小步，结果就是它不规律地做往返的曲折运动。股价的涨跌反映到股价上就是随机上下的运动。布朗运动最重要的统计学特征就是它的平均值和标准差。平均值就是短期的平均价格，它通常会向特定方向运动，这就是市场所认定的股价走向。标准差可以当成是股价与平均值的差值，它通过标准统计公式计算而来。对股价来说这就是波动性，它是衡量股价涨落随机性的参数。在股价对时间的图标上，反映波动性就是股价线条的粗糙程度。

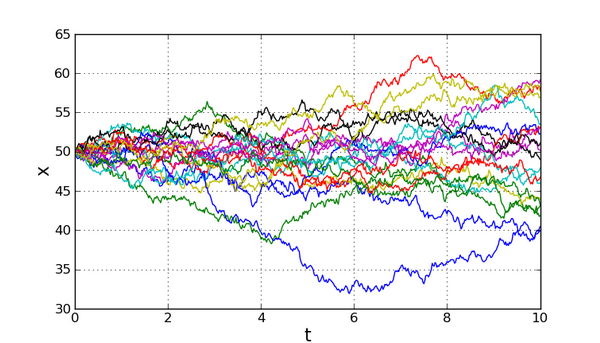布朗运动

布莱克-斯科尔斯采纳了巴舍利耶的看法。方程并没有给出期权的价值（购入或卖出期权的价格）。它是一个偏微分方程，表述的是其它量改变时价格对时间的变化。幸运的是，解这个方程可以得到一个特定公式显示卖方期权的价值，另一个类似的公式给出买方期权的价值。

金融危机中的市场交易员

布莱克-斯科尔斯公式早期的成功激励金融产业开发许多用于不同金融工具的相关方程。传统银行可以使用这些方程帮助据顶贷款和交易，并评估可能的利润并注意潜在的风险。但不那么传统的公司就没这么谨慎了。很快，银行就追随它们进入投机产业。

任何有关现实的模型都存在简化和假定。布莱克-斯科尔斯方程基于套利定价理论，在这里面漂移和波动性都是常数，但在现实的市场中这常常是错的。方程还假定交易没有成本，没有断短线交易的限制，总是可以以已知的无风险固定利率贷出和借入。显然，在这些方面和现实差距也非常大。

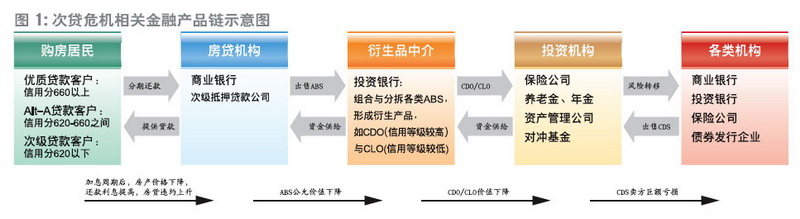次贷危机相关金融产品链示意图

在这些假定都成立时，风险很低，因为巨大的股市波动应该是非常罕见的。但是在1987年10月19日的黑色星期一，世界股市在几小时内损失了超过20%的市值。这样的事件在模型假定中根本就是不可能的。金融数学专家纳西姆·尼古拉斯·塔利卜(Nassim Nicholas Taleb)在他的畅销书《黑天鹅》中把这种极端事件称作黑天鹅。古时候，人类知道的所有天鹅都是白色的，“黑天鹅”的意思和我们现在说“飞猪”差不多。但在1697年，荷兰探险家魏勒姆·德·弗拉明戈在澳大利亚后来叫做天鹅河的地方发现了大批黑天鹅。因而这个词就变成了一种尚未证实的假定，但可能会成为一个广泛传播的谬误。

股市中的大起大落远比布朗运动预言的多得多。原因是不切实际的假定——忽略了可能存在的黑天鹅。但通常情况下模型和现实吻合非常好，因而人们的信心随着时间流逝而增长，许多银行家和交易员忘记了模型的局限性。他们把这个方程当成了辟邪的法宝，一种可以保护他们在发生问题以后免受批评的数学魔法。

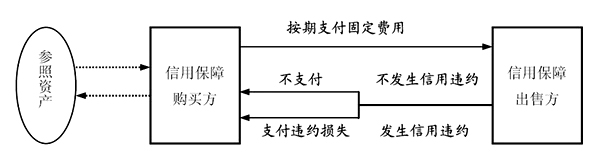信用违约互换

银行、对冲基金和其他投机人很快交易极大量复杂的金融衍生产品。其中一种是信用违约互换，这就像是保邻居家房子免于火灾的险种。这些金融工具定价后被认为是独立存在的资产，这意味这可以用它们来为其它债务作担保。在一切变得越发发杂以后，人们用模型来给与现实相去更远的衍生品估计价格和风险。有时衍生产品来自房地产，市场假定房产价格会永远上涨，把这种投资当成是无风险投资。

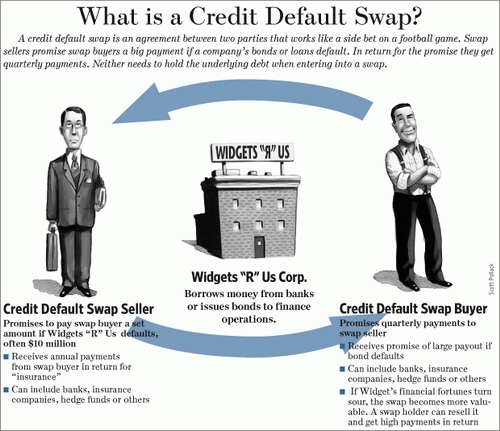什么是信用违约互换

布莱克-斯科尔斯方程源自数学物理学，在这个领域，时间一直在流动，变量也是平滑变化的。这些模型可能在金融世界中就不那么正确。传统的数理经济学不总是与事实吻合，在它们脱节的时候就会产生巨大的误差。因而，物理学家、数学家和经济学家总是在寻找更好的模型。

处于这种研究最前沿的就是数学分支复杂性科学，它使用模型来把市场当成大量个人在特定规则下的相互作用进行研究。这些模型显示了群体本能的毁灭性影响：市场交易员会模仿其他交易员的行为。基本上上世纪的每一场金融危机都是由于群体本能而爆发。群体本能让所有东西同时完蛋。如果工程师采取同样的态度，一旦某座桥倒塌，世上其它所有的桥也会同时倒塌。

研究生态系统可以发现，不稳定性是经济模型中的常见现象，主要是因为经济体系糟糕的设计。鼠标一点就能转移数十亿美元的便利可以迅速带来利润，但它也让动荡以前所未有的速度传播。

那这个方程是不是金融崩溃的罪魁祸首呢？是也不是。布莱克-斯科尔斯方程可能对崩溃有些贡献，但只有它被滥用才会如此。无论如何，方程只是这道金融不负责任、政治无能、奖励不当和管理缺失的大菜中的一味调料而已。

金融业者本该是定价专家，但他们所做的也就是随机的猜测而已。股票市场在二十年后又回到了原地。金融体系过于复杂，不可能靠充满错误的预感和直觉来操作，但目前的数学模型不能足够好地代表现实情况。我们对整个体系知之太少，它又是如此的不稳定。世界经济需要大刀阔斧的改革，我们需要更多而不是更少的数学家。数学可能是突飞猛进的科学，但它不是魔术。

编者后记：

随着金融危机的发生，金融业界越来越重视金融风险的控制，现在金融风险管理已经成为金融数学研究中的一个重要分支。对于布莱克-斯科尔斯方程中波动率是固定常数不合理假设，Steven L. Heston于1993年建立了随机波动率模型，Heston的模型中，不仅假设金融资产价格（如股票）是随机的，金融资产价格的波动率也是随机的。Heston模型较布莱克-斯科尔斯方程更符合世界市场。

这里还有一篇类似的文章《金融海啸与金融数学》。

【注】米达斯王是希腊传说中的人物，他得到了点石成金的本事，结果把自己的女儿变成了金人。