英国石油公司租用的“深海地平线”钻井平台发生爆炸并引发火灾。灭火及营救现场。

泄漏的浮油污染了墨西哥湾海面。

从墨西哥湾的漏油事件谈起

2010年4月20日晚，在距美国路易斯安娜州61公里的墨西哥湾海面上，由BP（英国石油公司）租用的“深海地平线”(Deepwater Horizon)钻井平台在从事Macondo油田开发作业时发生爆炸，并引发火灾，11名工作人员遇难。经过约36个小时的剧烈燃烧，“深海地平线”于22日沉入海底。两天后，在事故地点出现了严重的石油泄漏，破裂的油井管道每天向墨西哥湾海域倾倒5-10万桶原油（约8000-16000立方米），历时近三个月，造成了极为严重的环境事件将对美国以至世污染。直至7月15日，油井才被成功封堵。这是美国历史上迄今最严重的海上石油泄漏事件，也是本年度的重要焦点新闻。这次界的能源开发、环境保护和生产安全管理政策产生深远的影响。

当关注的焦点聚集到英国石油公司时，我们发现这个公司在墨西哥湾地区寻找油气藏方面取得了巨大的成功。按照公布的数据，出事的Macondo油田约有可供开发的原油5千万桶（约8百万立方米）。它的名字“Macondo”来自名著《百年孤独》中那个不幸的小镇，中文译为“马孔多”。实际上，在英国石油公司的开发版图上，“马孔多”只是一个小油田。2009年9月2日，英国石油公司宣布在墨西哥湾距休斯顿市东南400公里处发现了巨型油田Tiber。外界估计其总储量可达40-60亿桶，相当于约100个“马孔多”！英国石油公司的官方网站上例举了他们近几年在墨西哥湾深海地区开发的重要油田，预测产量都在1.5亿桶至6亿桶之间，包括Horn Moutain（2002年），Na Kika（2003年），Holstein（2004年），Mad Dog（2005年），Atlantis（2007年），Thunder Horse（2008年），等等，可谓硕果累累！

人们不禁会问：石油巨头们是怎样在墨西哥湾找到这些大油田的？以Tiber油田为例，此处的水深达到1200米，藏深埋在1万米以下！据古书《西游记》记载，孙悟空在皈依佛门之前曾闯入过建在海底的东海龙宫，取走了龙王的定海神针作为打斗兵器（又名如意金箍棒）。但是至今还没有可靠的证据显示任何人或神仙曾经达到过龙宫以下深9千米的地方。另一方面，深海石油开采的费用高得惊人，即使从事深海石油开发的公司拥有雄厚的资本和先进的技术，也不可能在茫茫无际的墨西哥湾到处打井窥测。以已经开发的Thunder Horse油田为例：它的水上钻井平台有3个足球场大，建筑在海水深度约为1800米的海面上。据估计英国石油公司等公司投入该项目的建造费用高达50亿美元！投资的高风险要求对资源的定位和估算有一套较准确的科学方法，尽量减少决策失误。所以深海寻宝既是与大自然的经济博弈，也是极具诱惑力的智力挑战。

秘密就在回声中

数学物理史上有这样一个有趣的问题：不用眼睛来看，仅仅通过聆听鼓的声音能否判断出鼓的形状？即所谓的“盲人听鼓”问题。该问题于1910年由丹麦著名物理学家劳伦兹(Lorentz)在哥廷根的系列讲演“物理学中的新、旧问题”中提出。它的背景来自于射线理论。

图1.能否以耳代目，“听出”鼓的形状？

我们知道，当物体的材料确定后，它的音色和其形状密切相关。在数学上，一个物体的音色可以由一串谱$\lambda_1\leq\lambda_2\leq\cdots$ 来确定，它们对应着物体的固有频率。“盲人听鼓”即是要求通过已知的谱来确定一个鼓面的形状。

劳伦兹在他的讲演中猜测鼓的面积可以由下面的公式确定

据说，当初大数学家希尔伯特认为在他的有生之年不可能看到这个公式的严格证明。但是一代宗师希尔伯特这次作出了错误的预测。不到两年时间，鼓面积的公式就被他的得意门生外尔(Weyl)证明了。而且证明方法采用的正是希尔伯特此前不久修炼出的独门绝技——积分理论。1954年，Pleijel证明了从鼓声中可以“听”出鼓的周长。1967年，McKean和Singer证明了从鼓声中可以“听”出鼓的内部是否有洞、有几个洞。直到1992年，Gordon等人构造出了两面奇怪的“同声鼓”（图1）：它们的形状不同，却有着相同的音色，单凭耳朵无法鉴别！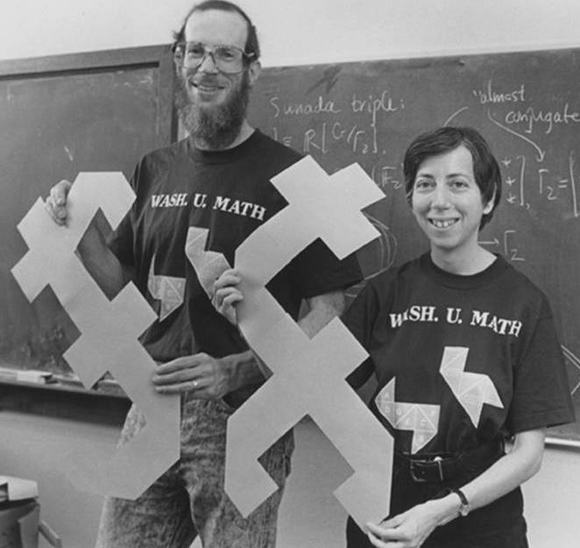

1992年，数学家Gordon,Webb和Wolpert找到了两面形状不同的“同声鼓”。

所以严格说来，“盲人听鼓”问题的答案是否定的。但是，对这个问题的研究启发了我们。当不能用眼睛直接观测时，以耳代目也能够获得关于物体形状的很多有用信息。举一个生活中的例子，夏天人们挑西瓜，总是把瓜放在耳边，用手拍一拍，有经验的人就知道瓜瓤熟不熟。深海区的石油探测就是应用了类似的原理。勘探地球物理学家希望能够叩问地球，用耳朵“听”出地下的地质构造，从而判断出油藏的准确位置和产量。

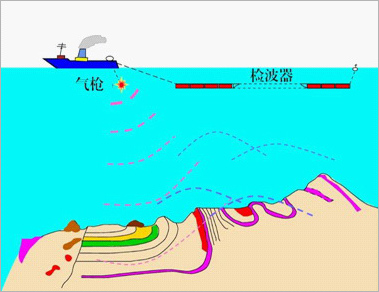图2.海上人工地震数据的采集

图2是海上石油勘探方法的示意图：数据采集船上带有气枪。当压缩空气被突然释放时，气枪会产生剧烈的爆炸声波。声波向地下传播，遇到构造变化会产生反射、散射和折射。这些回声中携带了地下的地质信息，被海面采集船拖带的检波器接收，记录为地震数据。海底宝藏的秘密就隐藏在这些数据里。

这是一个什么样的数学问题呢？

我们脚下的地球可以用三维坐标 $(x,y,z)$ 来标定，其中 $z$ 表示海平面下的深度。气枪的在海面的某个位置 $(x_s,y_s,0)$ 爆破，产生的声波

按照速度 $v(x,y,z)$ 在地下传播，满足波动方程

$\left(\dfrac1{v^2}\dfrac{\partial^2}{\partial t^2}-\Delta\right)p(x,y,z;t)=0$

在海面的 $(x_r,y_r,0)$ 处，检波器接收到了气枪产生的回声数据 $D(x_r,y_r,x_s,y_s,t)$。我们勘探的目的是要从采集到的地震数据D中猜出代表地质构造的函数v。

举一个最简单的例子，假设深度为Z米的地方有一个平层，声波传播速度是V米/秒。如果把气枪和检波器放在海面的 $(x_0,y_0,0)$ 处，气枪发射后经过时间 $T_0$ 秒我们听到回声，那么很容易知道

$T_0=\dfrac{2Z}{V}$

上面的公式里有两个未知数，Z和V，是不可解的。如果我们再做一次实验，将气枪和检波器分别放在 $(x_0-X,y_0,0)$ 和 $(x_0+X,y_0,0)$ 处（图3），这时听到回声的时间延长至 $T_1$ 秒，而且回声来自同一个地下反射点。根据勾股定理

$T_1=\dfrac{2\sqrt{Z^2+X^2}}{V}$

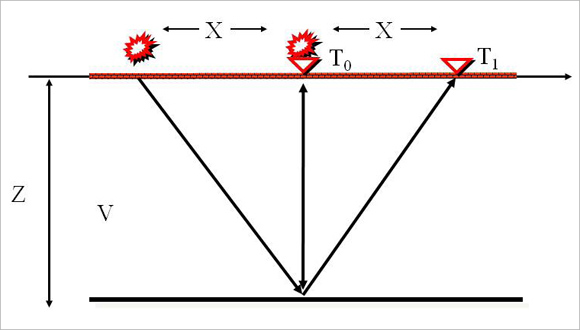图3：常速度、水平层模型可以通过两次实验来确定声波速度和反射层深度。

A

B

C

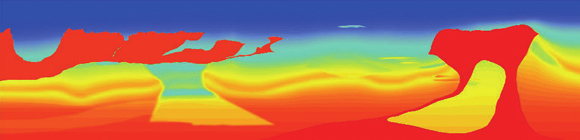D 图4：一个2维人工合成数据的成像实例。A:水面接收到的部分数据记录。B:经过去噪和校正过的部分数据记录。C:由数据分析出的背景速度模型。D:偏移成像后得到的地下构造变化细节。

通过两次实验，我们就可以联立上面的两个方程，同时求出声波速度V和反射界面深度Z。

真正的地下介质不可能是常速度，地质构造也不可能都是水平层。深海石油勘探需要揭示的是深埋地下，历经沧海桑田的复杂地貌，其困难程度可想而知。我们注意到，地下的速度函数 $v(x,y,z)$ 是一个三维数据体，而我们接收到的地震数据 $D(x_r,y_r;x_s,y_s;t)$ 却是五维的，信息中有二维的冗余度。这说明我们对地下的每个反射点做了很多次的声波反射实验，而这些五维的实验结果都来自同一个三维模型函数 $v(x,y,z)$。这样就可以通过数据的多次覆盖来提高对于地下构造判断的准确度。这个思路奠定了勘探数据处理的基础。经过数十年的摸索，地球物理学家找到了一些行之有效的解法。现行的勘探技术主要分为三步：

1．数据处理：海上采集到的数据有很多噪音干扰，比如海浪、背景噪声、相邻采集船传来的气枪回声，等等。另外，潮汐现象周期性地改变海水的深度，造成反射时间的偏差错落；气枪的震源效应和海面多次反射的混声也会引起反射信号的畸变（图4A）。所以我们要对数据进行“整容”，使之更清晰、更干净、更可信（图4B）。

2．速度建模：利用多次覆盖的试验数据来构建一个统一的地下模型。由于反射波的传播时间对速度的短周期变化不敏感，一步到位求解v(x,y,z)太困难。退而求其次，我们可以利用数据中的冗余信息构造一个粗眉大眼的近似速度$v_0(x,y,z)$。这如同绘画，先勾勒轮廓，敷设底色，留待下一步皴擦点染，刻画雕琢（图4C）。

3．偏移成像：从实践中，人们认识到在现有的方法和条件下，完全求出v(x,y,z)几乎是不可能的。必须采取更务实的态度，对v(x,y,z)做构造成像。也就是说只需要对速度函数的间断性变化进行比较精确地描绘，就可以提供给地质解释专家很多重要的石油埋藏线索。我们借助高性能计算机的帮助，将地震数据D和初始模型$v_0$综合起来进行处理，利用波动方程来推演各种反射信号的来龙去脉，输出的图像就显露出了地下山水的峥嵘面貌（图4D）。

漫话反问题

读者或许会感到石油勘探所涉及的数学问题有些别致。在大学的数学物理课堂上，通常是给定震源、边界条件和介质速度，列出声波方程，再来探讨声波现象或计算接收到的声波信号。但是现在我们的问题“反”过来了，通过接收的信号来探测什么样的介质能够产生这样的观测现象。为了体现这个差别，我们把这类问题称作“反问题”。而传统的“已知模型、初边值条件和源项来计算结果”的问题就叫做“正问题”。世间的事物或现象之间往往存在着一定的自然顺序，如时间顺序、空间顺序、因果顺序，等等。所谓正问题，一般是按着这种自然顺序来研究事物的演化过程或分布形态，起着由因推果的作用。反问题则是根据事物的演化结果，由可观测的现象来探求事物的内部规律或所受的外部影响，起着倒果求因的作用。可以看出，正、反两方面都是科学研究的重要内容。

以线性方程为例，它的正问题是已知矩阵A和向量 $\overrightarrow{x}$，求它们的乘积 $\overrightarrow{y}$

$A\overrightarrow{x}=\overrightarrow{y}$

它的结果是存在的、唯一的、而且稳定的。现在我们观测到的是带有噪音的数据

$\overrightarrow{y’}=\overrightarrow{y}+\overrightarrow{n}$

可以有很多种反问题的提法：

1.已知 $\overrightarrow{y’}$，分离信号和噪音，求出 $\overrightarrow{y}$；
2.已知 $\overrightarrow{y’}$ 和A，求出输入数据 $\overrightarrow{x}$；
3.已知 $\overrightarrow{y’}$ 和 $\overrightarrow{x}，$ 求出模型机制A；
4.已知 $\overrightarrow{y’}$，求出输入 $\overrightarrow{x}$ 和模型A，这时问题变成非线性。

上面任何一种反问题都比正问题要困难得多。

反问题通常体现了一种逆向思维。冯康先生在上世纪八十年代初曾经著文《数学物理中的反问题》，较早地介绍了这个新的研究方向。他将反问题的功能概括为“由表及里”、“索隐探秘”、“倒果求因”。在中国的传统文化中，只有智者高人才能透过现象看清本质，甚至参透因果，一语破的。科学化的反问题研究为我们在解决问题，增长智慧方面提供了很好的案例和方法论。

在西方，侦探小说有着悠久的传统，犹如武侠文化在中国。物理大师爱因斯坦在他与Infeld合著的《物理学的演化》一书中，反复将物理学家探寻自然奥秘的工作和神探的破案过程进行类比：

“自Conan Doyle（柯南道尔）演绎出精彩的福尔摩斯探案故事以来，在侦探小说中总会出现这样一幕：侦破者针对案件的某个方面搜集到他所需的线索。尽管这些线索看上去支离破碎、杂乱无章、怪诞费解，但是能力超凡的侦探认为不需要进一步调查了，眼前的证据已经足够，剩下的只是通过慎思明辨来发现事实背后的脉络。这时，他或者拉一段悠扬的小提琴曲，或者斜倚沙发，默默地叼着烟斗。突然间，灵光迸现！他不仅找到了对已知线索的合理解释，而且确信发生了一些迄今未了解到的情节。因为准确地推演了作案情境，他甚至知道可以到哪里去采集新的证据来证实他的推断。”

上面描述的破案过程就象是在求解反问题。当理性穿透现实的迷雾时，那种清澈、喜悦和潇洒的感觉是多么具有诱惑力！

我们下面看一个科学史上的著名的案例，来体会一下反问题的提出和解决过程。

1781年，天王星被确认为太阳系的第7颗大行星。40年后，法国天文学家布瓦尔(Alexis Bouvard)搜集了一个多世纪来的全部观测资料，包括了1781年之前的旧数据和之后的新数据，试图用牛顿的天体力学原理来计算天王星的运动轨道。他发现了一个奇怪的现象：用全部数据计算出的轨道与旧数据吻合得很好，但是与新数据相比误差远超出精度允许的范围；如果仅以新数据为依据重新计算轨道，得到的结果又无法和旧数据相匹配。布瓦尔的治学态度非常严谨，他在论文中指出：“两套数据的不符究竟是因为旧的观测记录不可靠，还是来自某个外部未知因素对这颗行星的干扰？我将这个谜留待将来去揭示。”

首先，布瓦尔等天文学家核查了1750年以后英国格林尼治天文台对各个行星所作的全部观测记录。结果发现，除天王星以外，对于其它行星的观测记录与理论计算结果都符合得相当好。似乎没有理由怀疑旧的天文观测唯独对天王星失准。既然如此，天文学家就需要对天王星的不规律运动作出科学的解释。

摆在天文学家面前的有两条路。

第一条路是质疑牛顿力学的普适性，或许万有引力定律不适用于距离太阳遥远的天王星，需要对之进行修正；

第二条路是寻找布瓦尔所猜测的“未知因素”。于是人们提出了“彗星撞击”、“未知卫星”和“未知行星”等多种可能。

图5：神探福尔摩斯

在科学研究中，困难是智者的试金石。1841年的暑期，还是英国剑桥大学二年级学生的亚当斯(J. C. Adams)就定下计划，不仅要确认天王星的轨道异常是否来自未知行星的引力作用，还要尽可能地确认这颗新行星的轨道，以便通过观测来发现之。这不仅是一个新问题，而且是一个反问题。因为过去总是已知一颗行星的质量和轨道，根据万有引力定律计算出它对另一颗行星产生的轨道摄动。而现在则相反，亚当斯要假定已知天王星轨道的摄动，来计算出产生这一摄动的未知行星的质量和轨道。由于未知因素很多，实际计算起来是相当复杂和困难的。

亚当斯于1845年彻底解决了这个反问题。他所运用的方法在当时是空前新颖的。令人遗憾的是，英国天文学家Airy先入为主地认为天王星的轨道问题是引力定律不再适用的结果，没有重视Adams向他提交的新行星的轨道计算结果。

几乎与此同时，法国人勒威耶(Urbain Le Verrier)独立地解决了同样的反问题。1846年9月23日，柏林天文台的Galle按照勒威耶提交的计算轨道着手观测，当晚就在偏离预言位置不到1度的地方发现了一颗新的八等星。连续观测的数据都与勒威耶的预测结果吻合得很好，证实这是一颗新行星。这时英国天文台才想起了亚当斯的工作，悔之晚矣。

案子破了。干扰天王星正常运行的那颗神秘天体正是太阳系的第8颗大行星——海王星！不仅长期困扰天文界的天王星轨道异常问题在牛顿力学框架内得到了完满解释，而且海王星的发现进一步验证了牛顿力学的正确性。

反问题的研究遍及各个领域，包括了定向设计，成像扫描，物性探测，逆时反演等很多技术，内容丰富，在工业、农业、国防、医学、金融、考古等各方面都有重要的应用。

知之惟艰

《古文尚书》中有“非知之艰，行之惟艰”的说法，是讲“知道一件事情并不难，难的是把事情做好”。数千年来，中国的先哲对“知易行难”和“知难行易”两个命题的谁是谁非论争不断。

在科学研究中，如果是求解一个正问题，“知易行难”的描述可能是比较贴切的。因为问题的规律、初始状态和模型都是已知的，我们只需要继承前人的知识，花费一些努力来计算、观测、考察各种现象变化。总的来说，这种研究工作是比较直接的。

反问题的研究重在探测和发现。如前面所述，虽然不能直接上天入地，但是通过求解反问题可以使得我们找到极遥远的天体和极幽深的宝藏，这就如同让我们有了神通。这种神通的得来并非容易。相对于正问题而言，反问题的研究要困难得多，可谓“知之惟艰”。这是因为反问题的求解往往违背了事物发展过程的自然顺序，从而使正问题中的许多良好性质不再满足。更何况我们搜集到的资料经常是真伪交杂、缺失含混的，这就更增加了求解的困难。尽管如此，解决反问题仍然像破案猜谜一样引人入胜。举一个文史方面的例子。《西游记》在中国是家喻户晓的神话名著，但是四百年来，这部小说的作者是谁却是一个谜团。由于早期刻本没有作者署名，清初刊刻时有好事者将著名道士丘处机的名字冠于卷首，混淆视听。直至民国初期，胡适先生通过书中的内证，认定作者的时代是明朝中叶以后，生活在元朝初期的丘处机属冒名顶替。接着，他和鲁迅先生一起搜罗史料，悉心考证，认为作者是明代嘉靖年间的淮安人吴承恩。但是由于大量史料散佚，直接证据阙如，这个结论也仍然受到质疑。目前提出的《西游记》候选作者约有十人之多，解未收敛，仍属悬案。

图6:发现天王星轨道异常现象的Alexis Bouvard(左，1767-1843)。成功地解决了这个难题并且预测了海王星轨道位置的John Couch Adams(中，1819-1892)和Urban Le Verrier(右，1812-1910)。

法国数学家哈达玛(Hadamard)认为一个有意义的物理现象的数学问题要满足适定性，即问题的解要具有存在性、唯一性和稳定性。这个观念深刻地影响了数学物理的发展。但是反问题的出现为人们提出了一大批病态的方程和问题，违背哈达玛的适定性要求，导致了研究上的困难。

我们前面提到的声波勘探技术就是一堆不适定性反问题的集合。我们简单举几个例子：

1．去除噪声：噪声是信号中的假信息。如果不能有效地切除噪声，可能将反问题的求解引入歧途；甚至导致矛盾方程，违背的解存在性。把金粒和沙粒混在一起是一件再容易不过的事情，但是沙里淘金就颇费周折。我们要区分噪音与信号的不同性质，通过一些巧妙的变换来去伪存真，纠偏校正。例如：高频噪音可以通过信号的统计性质来进行鉴别；特殊的低频噪声可以在频率域进行切除；干扰成像的横波、地滚波可以通过时空分布的特殊性在一些高维变换域中进行分离；多次反射可以用波场的线性变换来有效预测，等等。

2．层析成像：这是目前最流行的速度建模方法。它的主要部分是求解一个大型的病态线性方程，来估计各个网格点上的速度值。这个病态方程在一些区域是超定方程，需要利用信息的冗余度来提高解的可信度；而在另一些区域又是不定方程，存在严重的多解性。针对这类线性不适定性问题，前苏联Tikonov等学者提出了正则化方法。方法的主要思想是：利用对解和数据误差的先验估计可以将问题的求解限定在某个较小范围内。通过对问题的适当改造，将原本不适定的问题转化为适定的最优化问题求解。而且先验估计表明在一定精度下用正则化方法求得的解是合理的。这很像是猜谜：“申明：我是戴高乐派来的间谍”。如果只是“打一人名”，猜起来就比较困难。如果限定“打一当代国际政治人物”，范围缩小了，就可以通过筛选，找到最优的答案——“阿拉法特”。

3．偏移成像：尽管波动方程的正问题是一个线性方程，它的探测反问题却是非线性的，而且线性化后的逆算子求解也很困难。长期以来，地球物理学家用计算波动方程的共轭算子来替代求解逆算子，这样可以得到稳定的构造成像。所谓“计算波动方程的共轭算子”就是象《大话西游》中的月光宝盒一样让时光倒流，将地面接收的波场信号逆时间方向回传，从而找到产生反射的地下构造，显影造像。有趣的是，我们可以证明只要选择正确的求解域，对这种传统算法稍加修改，就可以得到有明确物理意义的稳定的反演解法。

4．衰减补偿：经典的波动方程假设声波在传播时能量是守恒的。但是实际的传播过程中，一部份声波能量会转化成热能耗散掉。而且震动快（高频）的波比震动慢（低频）的波更容易被吸收。求解这类现象的反问题就更困难了。因为时间倒流时方程的能量会不断增大，一方面记录中混杂的噪音会被迅速放大，另一方面一些有效信号在正演时被衰减殆尽而无从恢复。这时的反问题违反了解的稳定性，连月光宝盒都失灵了，必须借助某种具有正则化性质的月光宝盒来近似恢复历史本来面目。

实际上，石油勘探的反问题经常存在着信息先天不足的缺陷。我们在医院做B超诊断时，探头可以围绕全身，这样就能够完整地接收超声波的各种反射和散射信息，有效地对病灶进行探测。但是对于地下构造进行勘探时，我们只能把爆炸源和接收器放置在地面或海面的有限范围内。很可能我们的声波达不到地下的一些构造位置；或者虽然声波能够达到，但是反射信号会传播到很远的地方，不能被接收器采集记录。这就造成了很多地下的成像盲区（图7）。另外，现有的偏移成像算法还不能完全解决由于多解性所导致的假像问题（图7），这些假的构造会误导地质解释人员做出误判。在实际生产中，我们需要通过试验和分析，对这些具体问题作出判断和解释。

用传统的眼光来看，存在性、唯一性和稳定性，三者之一不满足就称为不适定性问题，这样的问题是不值得研究的。但是反问题的研究开阔了人们的视野，认识到这样的问题是大量存在的，并且有着重要的研究和应用价值。反问题有着特殊的困难，它向我们提出了许多在认识论、方法论中富有挑战性的课题，深化了对客观现象的理解。因而反问题的研究确有它独立的价值。

数学有价？

回想十二年前，笔者从事应用数学的博士后工作，当时困惑我的问题是如何将“应用”与“数学”这两件事统一起来。记得闲暇之余观看了一部香港电影《南海十三郎》，讲的是上个世纪三十年代的天才粤剧作家江誉镠，艺名南海十三郎。其中有一段关于唐涤生欲拜南海十三郎为师的情节，至今印象颇深。

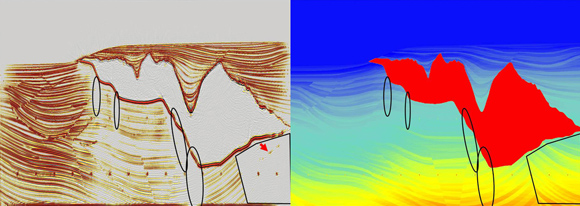图7：一个理论合成记录的偏移成像结果（左）和真实的速度模型（右）。曲线框标示的区域是由于观测方法限制所造成的偏移成像盲区。红色箭头所指是偏移成像算法得到的假像。

南海十三郎：“你为什么要拜我为师？”

唐涤生：“因为我要证明文章有价！”

后来唐涤生成为一代巨匠，不仅缔造了粤剧史上的辉煌，而且其剧作浑然天成，辞藻清隽雅丽，成为传诵不衰的经典。虽然中年早逝，他的一生很好地诠释了“文章有价”的信念。

那么数学有价吗？这是一直萦绕在我心中的问题。

进入勘探地球物理界以后，才发现生产上所提出的富有挑战性的数学问题俯拾皆是，我们几乎每天都在从事索隐探秘的研究活动，颇为引人入胜。

以偏移成像技术为例。早期的计算机内存小、速度慢，而勘探资料处理的数据量和计算量都很巨大。从70年代到90年代，资料处理人员不得不对数据进行简单的预处理，忍痛割爱，将辛辛苦苦采集来的五维地震数据压缩成三维，送入计算机进行反演成像。在当时，采用这种丢失大量原始信息的粗糙方法实在是迫不得已。

90年代末，勘探界发展了积分法偏移技术，删繁就简，运用高频渐进分析的技巧，把成像步骤简化为常微分方程求解和积分求和两部分，有效地节省了计算量，终于可以对全部采集数据作偏移处理。但是一阵兴奋过后，人们发现这种简化方法远不能满足墨西哥湾地区复杂地形勘探的要求。

进入新千年，由于采用了并行计算机群技术，更精确的微分法偏移被引入生产。受当时计算机的内存限制，生产上需要将波动方程变形为单程波方程，降维求解。单程波方程是地球物理学家们在70年发明的一种独门功夫，其道法心诀与发轫于60年代数学界的拟微分算子理论暗合。

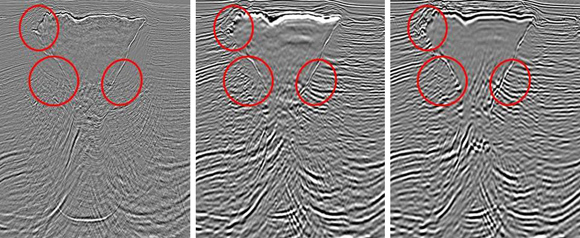图8：一个墨西哥湾地区的生产实例展示了不同偏移算法的成像效果。左：2001年得到的积分法成像结果；中：2005年得到的单程波偏移成像结果；右：2007年得到的逆时偏移成像结果。

另一方面，一些公司领异标新，为积分法注入了新的功力，实现了升级版的射线束偏移，使得算法更灵活、更准确，成像效果令人耳目一新。

与此同时，数据采集方法也得到了很大改进。英国石油公司率先采用了宽方位角采集技术，利用大量的反射信息来有效地减少成像的盲区，也使得地震数据量猛增几倍到几十倍。

2005年后，逆时偏移方法应运而生。这种方法直接求解声波方程，看似返璞归真，实际功能强大。不管是反射波、折射波、散射波、回转波、棱柱波，无论信号的来路多么怪异，逆时偏移都可以因势利导，让它们复原归位。这种方法能够对复杂的地下构造做出精确的成像，成为墨西哥湾地区独领风骚的生产技术。

图8的实例显示了不同时期、不同算法对地下构造成像质量的影响，一路走来，进展令人振奋。

2008年底，生产上实现了各向异性的逆时偏移算法，突破了传统偏移算法对速度所要求的各向同性假设。对于这种偏移，我们要假设声波沿着各个方向的传播速度均不相同，虽然计算成本和反问题的不确定性都大幅度增加，但使用起来招法更加灵活，在墨西哥湾地区得到了良好的效果（图9）。

进入2010年，为了更准确地构建速度模型并进行岩性分析，生产要求逆时偏移对地下构造输出高维全息照片。如果我们考虑理想情况，这需要将五维的地震数据输入逆时偏移，经过六维的偏微分方程计算和七维的拟微分算子变换，再叠加输出五维的成像信息。这必然导致巨大的计算工作量和复杂度。产业的需求敦促成像方法更上一层境界，再一次挑战数学算法和软件开发的极限。

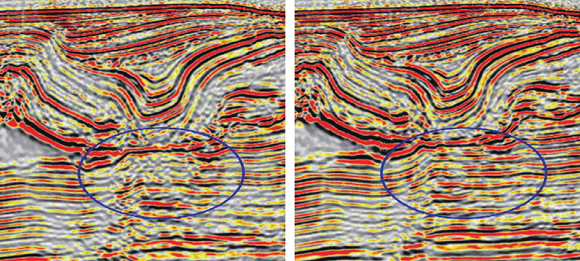图9：墨西哥湾地区某油田附近的偏移成像效果对比。 左：各向同性的逆时偏移成像结果；右：各向异性的逆时偏移成像结果。

无论勘探计算中的数学方法多么精巧，我们始终都是在猜谜。谜底只有在实际钻井后才能揭晓。在两年前的一次感恩节晚会上，一位在石油公司工作的朋友姗姗来迟，神情疲倦。一问才知，公司刚刚打了一口干井，数千万美元的投资泡汤了。一大早他所属的部门临时召集会议，检讨决策失误原因，其中之一就是偏移处理的成像剖面在井位处模棱两可，难以准确判断地下的构造。这个经历使我感到我们的科研工作不是纸上谈兵，在应对挑战的同时我们还承担着重要的生产责任。

在过去的十多年间，石油勘探的计算方法发生了日新月异的变化，而且技术的更新有加速的趋势。这种生命力和创造力来自巨大的商业利益的驱动。在这里，每项数学技术的商业价值都是可以计算的。也正是由于勘探技术的不断进步，石油巨头在墨西哥湾深海区的石油开采屡获创收。

展望未来，地震勘探的反问题远没有解决。实际的地震波的传播比声波现象更复杂，需要用21个弹性参数来描述。各向异性的声波偏移只是向这个方向迈出的第一步。另外非弹性吸收效应在偏移中的补偿还刚刚起步。随着研究的深入和计算技术的提高，传统的偏移成像方法也面临新的技术挑战。直接求解非线性反问题得到高精度的速度模型成为当下的热门课题，很多理论、算法和实际困难都有待克服。

1700多年前，数学家刘徽在他的名著《九章算术注》的序文里指出，数学的功用可以达到“虽幽遐诡伏，靡所不入”。我们希望更好地运用数学物理方法来探索自然的奥秘，绘出更准确、更清晰的地下寻宝图。

致谢：本文作者感谢BP公司和SMAART课题组提供的理论合成数据。同时感谢CGGVeritas公司管理层长期以来对科研工作的重视与支持。

本文摘自：《数学文化》第三期