大自然给了我们许多不容易被人类数字系统表示的重要常数，如$\pi$和$e$。例如，$\pi$的前50位数字

$$\pi = 3.14159265358979323846264338327950288419716939937510\ldots $$

只提供了这个重要数的一个逼近，因而我们觉得有必要更深入地了解这样的数。我们也可能会问这些重要的常数之间是否有关联。例如，乍一看，$\pi$和$e$似乎在不同的数学领域出现，所以如果发现它们的值可通过简单的方式联系在一起，这将是非常值得注意的。

在这篇文章中，我们将探讨圆的周长与直径的比$\pi$怎样以惊人的精度计算出来。事实上，我们将看到如何深入到$\pi$的十六进制表示的内部来计算我们希望的任何位数。我们还将介绍相关的新算法，使我们能够探讨各种数值常数是否存在简单的关系。

虽然现实世界的应用不需要准确到50位数字的$\pi$，然而计算$\pi$的历史是丰富的，其动机主要是出于我们自己的好奇心。对于计算科学家来说，计算问题提出像“数如何有效地相乘”这样的技术性挑战，他们的解决方案有着广泛的应用。

早期的圆周率计算

古希腊数学家阿基米德是仔细研究$\pi$的先驱之一。他的技术从一个周长为$2\pi$的单位圆开始，然后用内接和外切正多边形的周长来逼近圆周长。

例如，下图所示的两个正六边形的周长将给出$\pi$的上、下界。

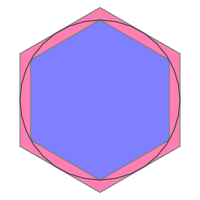
通过增加多边形的边数，我们可以得到更好的上下界。

如果令$a_n$和$b_n$分别表示外切$n$-边形（标以红色）和内接$n$-边形（标以蓝色）的周长，则有

$$b _ { n } < 2 \pi < a _ { n } \quad \text { and } \quad 2 \pi = \lim _ { n \rightarrow \infty } a _ { n } = \lim _ { n \rightarrow \infty } b _ { n }$$

当$n = 6$时，容易计算出周长

$$a_6 = 4 \sqrt{3}, \; \; b_6 = 6. $$

本质上利用三角中的半角公式，阿基米德确定出当边数加倍后周长如何变化，从而得到循环公式

$$a_{2n} = \dfrac{2 a_n b_n}{a_n + b_n}, \; \; b_{2n} = \sqrt{a_{2n} b_n}. $$

用这一方法，我们有上下界

$$\frac { 223 } { 71 } < \pi < \frac { 22 } { 7 }$$

1600年左右在荷兰工作的德国数学家Ludolph van Ceulen采用了阿基米德的计术算出了$\pi$的前35位，并将它的上下界刻在自己的墓碑上。

不久以后，微积分的发展给了计算$\pi$的新方法，我们现在介绍当中的一个。记得几何级数具有形式

$$1 + r + r^2 + r^3 + \ldots. $$

即，和式中的每一项是前一项乘上一个固定数r。假如r的绝对值小于1，级数收敛并容易赋值。记和为S，

$$S = 1 + r + r^2 + r^3 + \ldots. $$

再把左右式乘以$r$

$$r S = r + r^2 + r^3 + r^4 + \ldots. $$

第一式减去第二式，得到$(1-r)S = 1$，因此

$$S = 1 + r + r^2 + r^3 + \ldots = \dfrac{1}{1-r}. $$

如果令$r = - u^2$，则得到

$$\dfrac{1}{1+u^2} = 1 - u^2 + u^4 - u^6 + \ldots. $$

两边积分后就有

$$\begin{aligned} \arctan x & = \int _ { 0 } ^ { x } \frac { 1 } { 1 + u ^ { 2 } } d u \\ & = \int _ { 0 } ^ { x } \left( 1 - u ^ { 2 } + u ^ { 4 } - u ^ { 6 } + \ldots \right) d u \\ & = x - \frac { x ^ { 3 } } { 3 } + \frac { x ^ { 5 } } { 5 } - \frac { x ^ { 7 } } { 7 } + \ldots = \sum _ { k = 0 } ^ { \infty } ( - 1 ) ^ { k } \frac { x ^ { 2 k + 1 } } { 2 k + 1 } \end{aligned}$$

如果让$x = 1$，我们得到通常归功于莱布尼茨的$\pi$的表达式

$$\pi = 4 \arctan 1 = 4\left(1 - \dfrac{1}{3} + \dfrac{1}{5} - \dfrac{1}{7} + \ldots \right) = 4 \displaystyle \sum_{k=0}^{\infty} (-1)^k \dfrac{1}{2k+1}.$$

真正计算中，这不是计算$\pi$的特别有用的方法，因为它收敛太慢。这里是它的前几项得到的逼近值：

$n$	$\mbox前n项的和$
$1$	$4.0000$
$2$	$2.6667$
$3$	$3.4667$
$4$	$2.8952$
$5$	$3.3397$
$6$	$2.9760$
$\cdots$	$\cdots$
$1000$	$3.1406$
$1001$	$3.1426$

如你所见，加了1000项后，我们才得到$\pi$的前三位数字。

欧拉找到一个更有用的公式：

$$\dfrac{\pi}{4} = \arctan(\dfrac{1}{2}) + \arctan(\dfrac{1}{3}),$$

它可用复数相乘简单解释之。记得复数乘积$ab$的幅角等于$a$和$b$的幅角之和。欧拉的公式则由$(2 + i) (3 + i) = 5 + 5i$得到。利用上面反正切函数的级数表达式，就有

$$\pi = 4 \left( 1 / 2 - \frac { 1 } { 3 } ( 1 / 2 ) ^ { 3 } + \frac { 1 } { 5 } ( 1 / 2 ) ^ { 5 } + \ldots \right) + 4 \left( 1 / 3 - \frac { 1 } { 3 } ( 1 / 3 ) ^ { 3 } + \frac { 1 } { 5 } ( 1 / 3 ) ^ { 5 } + \ldots \right)$$

相加两个级数的前十项，就得到一个近似$3.1415925796$，精确到前七位。这个公式和涉及反正切的其他类似公式，最终产生$\pi$的前几百个数字。

当然，所有这一切都在计算机问世之前实现。最近，Yasumasa Kanada采用了类似的反正切公式，花了一台超级计算机大约600个小时算出$\pi$超过一万亿个的位数。

BBP公式

如果我们想计算$\pi$的一个特定数字，以上列出的技术要求我们使用高精度的算术来计算它前面的所有数字。20世纪90年代的中期，一个了不起的新的计算公式被David Bailey、Peter Borwein和Simon Plouffe (BBP)发现：

$$ \pi = \displaystyle \sum_{k=0}^{\infty} \dfrac{1}{16^k} \left( \dfrac{4}{8k+1} - \dfrac{2}{8k+4} - \dfrac{1}{8k+5} - \dfrac{1}{8k+6} \right).$$

我们稍后描述一下这个公式的发现。首先我们将看到这个公式如何让我们直接计算它的一个十六进制数字，而不必算出前面的所有位数并且不使用高精度算术。

要了解这是如何工作的，让我们考虑计算$\ln(2) = 0.69314718056\ldots$的一个类型相似的公式。记得

$$\begin{aligned} \ln ( 1 + x ) & = \int _ { 0 } ^ { x } \frac { 1 } { 1 + u } d u \\ & = \int _ { 0 } ^ { x } \left( 1 - u + u ^ { 2 } - u ^ { 3 } + \ldots \right) d u \\ & = x - \frac { x ^ { 2 } } { 2 } + \frac { x ^ { 3 } } { 3 } - \frac { x ^ { 4 } } { 4 } + \ldots \\ & = \sum _ { k = 1 } ^ { \infty } ( - 1 ) ^ { k + 1 } \frac { x ^ { k } } { k } \end{aligned}$$

故有

$$\ln ( 2 ) = - \ln ( 1 / 2 ) = \sum _ { k = 1 } ^ { \infty } \frac { 1 } { 2 ^ { k } k } = \frac { 1 } { 2 } + \frac { 1 } { 2 ^ { 2 } \cdot 2 } + \frac { 1 } { 2 ^ { 3 } \cdot 3 } + \ldots.$$

让我们看看$\ln(2)$的二进制数字：

$$ \ln(2) = .d_1d_2d_3d_4\ldots = d_12^{-1} + d_22^{-2} + d_32^{-3} + d_42^{-4} + \ldots. $$

如果我们想计算第$n+1$个数字$d_{n+1}$，上式两边乘上$2^n$:

$$2 ^ { n } \ln ( 2 ) = d _ { 1 } 2 ^ { n - 1 } + d _ { 2 } 2 ^ { n - 2 } + \ldots + d _ { n } + d _ { n + 1 } 2 ^ { - 1 } + d _ { n + 2 } 2 ^ { - 2 } + \ldots = d _ { 1 } d _ { 2 } \ldots d _ { n } \cdot d _ { n + 1 } d _ { n + 1 } \dots$$

注意到，我们希望找到的数字$d_{n+1}$是小数点后面的第一位数字。因此，如果$2^n \ln(2)$的小数部分小于$0.5$，则$d_{n+1} = 0$，否则$d_{n+1} = 1$。所以我们只需要计算$2^n \ln(2)$的小数部分，记为$\{2^n \ln(2)\}$。它的计算如下：

$$\begin{aligned} \left\{ 2 ^ { n } \ln ( 2 ) \right\} & = \left\{ 2 ^ { n } \sum _ { k = 1 } ^ { \infty } \frac { 1 } { 2 ^ { k } k } \right\} \\ & = \left\{ \sum _ { k = 1 } ^ { \infty } \frac { 2 ^ { n - k } } { k } \right\} \\ & = \left\{ \sum _ { k = 1 } ^ { n } \frac { 2 ^ { n - k } } { k } \right\} + \left\{ \sum _ { k = n + 1 } ^ { \infty } \frac { 2 ^ { n - k } } { k } \right\} \\ & = \left\{ \sum _ { k = 1 } ^ { n } \frac { 2 ^ { n - k } } { k } \right\} + \left\{ \sum _ { k = n + 1 } ^ { \infty } \frac { 2 ^ { n - k } } { k } \right\} \end{aligned}$$

最后一行中的各项可有效地用著名的二进制幂算法计算。第二个和式的总和小于$1/(n+1)$，所以如果$n$很大，它的贡献很小。如果还记得我们只需要确定小数部分是小于或大于$0.5$，我们只要在第二个和式中计算足够多的项就可解决问题。

回到BBP公式

$$\pi = \displaystyle \sum_{k=0}^{\infty} \dfrac{1}{16^k} \left( \dfrac{4}{8k+1} - \dfrac{2}{8k+4} - \dfrac{1}{8k+5} - \dfrac{1}{8k+6} \right),$$

我们看到，每一项都有的$16^k$能让我们以类似的方式计算$\pi$的任一位十六进制数字，而不必计算它之前的数字。

$\pi$的十六进制数字从第一万亿零一次开始，实际上是B4466E8D215388C4E014。最近的工作已成功地计算出第一千万亿位($10^{15}$)十六进制数字。

PSLQ算法

证明BBP公式的方法之一是考虑积分

$$\displaystyle\int_0^{1/\sqrt{2}} \dfrac{4\sqrt{2} - 8x^3 - 4\sqrt{2} - 8x^5}{1-x^8} dx. $$

一方面，运用大部分学生所熟悉的部分分式技巧，可以证明这个积分等于$\pi$。另一方面，几何级数表明

$$ \dfrac{1}{1-x^8} = 1 + x^8 + x^{16} + x^{24} + \ldots. $$

这使我们能够将被积函数写成级数形式并逐项积分。把这两个事实放在一起，就给出BBP公式。

但BBP公式是如何被发现的？当然不是通过刚才所描述的积分。相反，BBP公式来自于检测实数集合之间整数关系的所谓的PSLQ算法。

举例来说，如果我们有一组实数$x_1, x_2, \ldots, x_n$，我们可能会问是否存在整数$a_1, a_2, \ldots, a_n$，其中至少有一个不为零，使得

$$a_1 x_1 + a_2 x_2 + \ldots + a_n x_n = 0. $$

对于给定的实数，可能没有一组整数$a_1, a_2, \ldots, a_n$满足上述关系。但如果有，PSLQ算法会找到这样一组整数。

检测整数关系有着悠久的历史。例如，欧几里得在《几何原本》的第十章考虑过这个问题$n=2$的情形。为了解释欧几里得的算法，我们把两个实数称之为$A$和$B$。要求有整数$a_1$和$a_2$使得$a_1 A + a_2 B = 0$等价于问是否存在实数$C$以及整数$n$和$m$满足$A = nC$和$B = mC$。（在这种情况下，欧几里得说$A$和$B$是公度的。）

对正数$A$和$B$，欧几里得的著名算法如下运行：

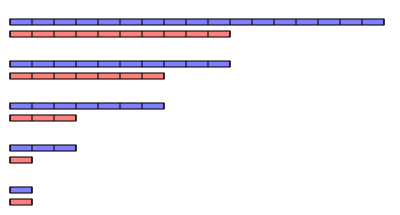
• 如果$A = B$，则$A$和$B$有整数关系，算法以$C = A = B$终止。

• 两个实数的较小者称为$B$。令$A = A - B$。

• 重复上述步骤。

如果该算法终止，那么我们已经发现$C$，使得$A = nC$和$B= mC$。如果我们让

$$ a_1 = - \dfrac{B}{C} \; \; \mbox{及} \; \; a_2 = \dfrac{A}{C}, \; \; \mbox{则} \; \; a_1 A + a_2 B = 0, $$

从而证明一个整数的关系。

算法的两个图示如下给出，其中线段的长度代表了$A$和$B$的值。在第一种情况下，我们发现$A$和$B$有公度，并得到$C$。

在下一种情形，$A = \pi, \; B = e$。

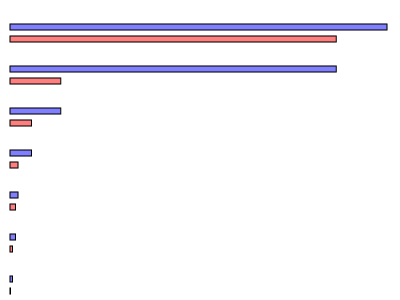
经过几个步骤后，该算法还没有终止。当然，这并不意味着如果我们让它运行一段时间它还是不会停止；在实践中，我们还不能确定该算法将无限期地运行下去。然而，我们能注意到，如果算法尚未终止，那么我们可以保证$C$比$A$的当前值要小。这反过来又给出整数$a_1$和$a_2$的下限。

自欧几里得的时代起，将欧几里得算法推广到两个实数以上的情形已被欧拉、雅可比、庞加莱等人考虑过。1979年，Helaman Ferguson和Rodney Forcade发现了一个算法，该算法此后被Ferguson、Bailey及Steve Arno精细化成PSLQ算法。

PSLQ算法类似于欧几里得算法，它推广成：如果有一个整数关系，该算法将在发现它时终止。如果算法不终止，就没有整数关系。当然，我们可能永远不知道实践中该算法会不会终止；然而，如果算法运行了一段时间后不终止，我们可以确定关系中整数的上下限。

执行PSLQ算法对自身提出挑战，因为计算机只能使用有限精度的运算。例如，我们为之寻求整数关系的实数在计算机内存中只能用有限多个数字近似。此外，算法中需要的真实运算受制于舍入误差。

正因为如此，PSLQ算法的实施不能够产生明确的整数关系。相反，该算法只建议可能的关系，而整数关系存在的证明则需要与算法独立地提出来。

BBP公式通过应用PSLQ算法找到$\pi$和8个常数

$$X_j = \displaystyle \sum_{k=0}^{\infty} \dfrac{1}{16^k (8k+j)}, \;\;\; j = 1, 2, \ldots, 8 $$

之间的一个整数关系以及作者称之为“受启发猜测和广泛的搜索”而被发现的。然后该公式通过上述的积分方法证明。

BBP公式使我们能计算$\pi$的第$n$个十六进制数字而不必计算前$n - 1$位。目前我们不知道是否存在类似的公式，使我们以同样的方式来计算任意一位十进制数字。

除了发现BBP公式外，PSLQ算法还找到了其他的一些用途。例如，该算法可用于探讨一个给定的实数是否是代数数（即一个整系数多项式的根）。此外，PSLQ发现了涉及量子场论中费恩曼图赋值所产生的常数的一些恒等式。

顺便说一下，一直从事整数关系探测算法基本数学工作的Helaman Ferguson，也是一个用艺术来表现美和数学理解的雕塑家。

原文链接:	http://www.ams.org/samplings/feature-column/fcarc-pi
作 者:	David Austin，Grand Valley State University
翻 译:	丁玖，密执安州立大学博士，南密西西比大学数学教授
校 对:	汤涛，香港浸会大学数学讲座教授