吃喝和欢乐:确保安全
大多数数学家在派对中常被重复问及一些问题。其中数学有什么用处就是一个常听到的问题。然而,即使在充满美味食物的派对场景中,数学也可以成为一个不可或缺的要素。事实上,数学对于食品工业可以是至关重要的。从农场到刀叉,从刀叉到(抱歉不雅之词)下水道,数学总在那里。可以通过数学建模对安全生产、储存、检测、运输、烹饪、饮食和食物(及药品)消化等过程给于解释。尤其重要的是,它有助于决定做饭、吃饭和食物消化是否安全以及如何做到安全。
在这一系列的两篇文章中,我将关注数学涉及到食品尤其是食品安全和健康的两种方式。在这篇文章中,我们将讨论数学如何告诉我们微波炉里最安全的食物烹调方式。另一篇文章谈论的是食物消化以及混沌理论如何用于求得药物消化的最佳途径。
唯恐亲爱的读者认为这有点浪费时间而不是一个严肃的科学应用,让我们想一想不起眼的饼干吧。一个可爱的数学应用有助于预测饼干何时开裂,从而可以减少它们制造时开裂的机会。“那又怎样?”面对这个惊人的事实《今日程序》(Today Programme)的采访者问。好吧,要知道饼干行业和辅助食品行业雇用1.5万人,代表着英国整个制造业产值的15%,每年对英国经济的贡献超过10亿英镑,所以对这个行业的理论指导会很有意义。从另一个角度问,你会买一包破裂的饼干吗?
 味道不错的巧克力,其中有很多数字应用
味道不错的巧克力,其中有很多数字应用 在微波炉烹饪食物
人们都知道,当今烹饪食物(或至少加热)的流行方法是使用微波炊具。在这样一种炊具里,微波由磁控管产生并通过波导管或天线进入炉腔。这样就建立了一个电场,在烤炉内照射放在那里的食物。微波穿透食物,并通过食物中各种分子之间的振动引起的摩擦,改变食物潮湿部分的分子方向,导致食物材料的加热,因而使食物中的水变成蒸汽。
这个过程的一个问题是该电场可以有驻波模式,它在电场相对薄弱的地方可能导致局部的“冷点”。如果食物被放置在一个寒冷的地方,那么它的温度可能较低,因而很难煮熟(见下图)。这对于公众健康具有非常重大的影响。如果食物不够热,它里面的细菌则不会被杀死,这可能导致严重的食物中毒。为避免这个问题,食物可以通过一个转盘在电场中旋转,或者电场本身就有一个旋转金属风扇来“搅拌”食物。
 微波炉和四个温度探针用来测试模型的预测能力
微波炉和四个温度探针用来测试模型的预测能力 使用数学,我们可以模拟食物在微波炉里的加热过程,比较转盘和搅拌模式对微波炉设计的有效性。要做到这一点,我们需要做三个计算。首先,我们需要找到食物中来自于微波的电磁场。其次,我们必须弄懂这个场如何加热食物。最后,我们要算出在烹调过程中食物里有多少水分会变成蒸汽,注意到许多食物最初有$80\%$的水。这最后一项则是计算的一个主要部分。
一种困难的方式
最直截了当的计算方式来是求解电磁辐射的麦克斯韦方程组,这样可以模拟全方位三维电场。用这个途径,我们可以通过求解淀粉和水混合材料的多孔介质方程组来找到温度分布。
这种方法的问题是,首先计算非常耗时,通常几个小时,更糟糕的是计算结果往往不可靠并且难以核实。这使得当你的问题参数改变时,例如食物放在转盘上或用搅拌模式,计算结果很难告诉我们究竟发生了什么。其次,这种方法对选取参数的过程和方式几乎没有直接的洞察力。第三,微波烹调对炉腔几何、食物的形状和类型甚至空气中湿度的小变化都很敏感。这意味着,计算结果常常依赖于某个特定日期和某个特定微波炉的电场。
 烤箱内食物的一个热相机图像,展现了中心处明显的冷点
烤箱内食物的一个热相机图像,展现了中心处明显的冷点 一个更简单的方法
更具有代表性的是一类家用微波炉的平均行为计算,在此计算中各种参数变化的不同影响更加透明。这往往是数学建模方法可以最可取的地方:一点点的数学就可以得到计算机长时间计算才能得到的结论,并常常给出更直接有用的结果。
与大众的误区恰恰相反,微波并不从里面煮食物。相反,微波从外面渗透,当传递到食物内时被吸收,并在这一过程中失去能量。微波炉中的食物最热的部分通常只是在表皮之下。如果食物过大,那么它的内部很难接收到微波的能量。这就是为什么微波食品的制造商普遍坚持,在微波炉里加热一段时间后要搅拌食物,以确保它所有的部分都达到均衡的温度。
为了数学建模,想象我们在微波过程中的时刻t坐在食物的点(x, y, z)处,其中x被看成进入到食品内的深度。在这一时刻的空间点,能量P(x, y, z, t)正从微波场转移到食品内的该点。同时考虑到这个过程也有一些传热损失,热被转移到邻近的分子。从数学上讲,热损失由表达式
描述,其中T(x, y, z, t)是(x, y, z)点在时刻t的温度,$\frac{\partial^2 T(x, y, z, t)}{\partial x^2}$是T关于x坐标的二阶偏导数(对y和z也是类似的)。常数$\kappa$是食物的导热系数,用来衡量其导热能力。
微波功率P将能量输进食物,使之加热。然后,热能通过传导损失。微波加热和热损失共同导致温度T在各点随着时间而改变。我们将温度T对时间的变化率表示为偏导数$\dfrac{\partial T}{\partial t}$,简写成$T_t$。$T_t$乘上该食物的比热容量$c$(这是食物改变温度所需的热量)平衡了以上所述的热量变化。因此我们得到方程
这里必须指出,如果温度T达到100度,则这个方程需要改变,这是因为需要额外的能量将水变成蒸汽然后再加热蒸汽,但为了简单起见,这里我们将忽略这个细节。
要从这个公式得出在时间t时(x, y, z)的温度T(x, y, z, t),我们就必须知道P(x, y, z, t)。正如之前讨论的,找到P将会非常困难,但是对搅拌模式微波炉或有转盘的微波炉可以发现它的一个很好的近似。这个近似表明,只要你加热的食物直径大于2厘米,当电场穿透食物时其整体呈指数衰减。
因此,可以使用焓方程获得比由麦克斯韦方程组的完整解更简单的电场描述。这个简化导致了
这里P是食物表皮上的微波能量,它比P(x, y, z, t)容易计算得多,x是进入该场的距离,d是一个常数,称为穿透深度。它是微波开始得到强烈吸收的长度,大约8毫米。
上面这个线性方程在规则区域里,可以用所谓的傅里叶级数方法求解(可在捕捉波博客中找出更多信息)。但是,用这些简化方程的数值逼近更容易。在台式电脑上可以很快找到这样的解。这样给出的近似,通过对比实验得到的温度和水分后,发现这些数值近似出奇的准确,这给予使用这个模型进一步设计的信心。整个方法的成功归功于数学、数值方法、物理模型和谨慎使用实验数据的有机结合。这是把不同思想结合起来有效解决工业和应用数学问题的一个典型例子。
测试模型
最后让我们看看一些结果。我们在下面的图中显示四探针测量(可以通过微波炉照片上看到)的加热湿润淀粉类食物的温度结果。第一个探头是在食物的外面,然后向内移动,第四个探头在食物的中心。
蓝线显示的是大量的实验结果,红虚线是数学预测。这两者之间的相合性非常好。你可以看到,约三分钟后第一个探头的温度达到摄氏100度,并停留在此温度。那里所有的微生物将被杀死。然而,第四个探头的温度五分钟后才达到100度。如果你的食物只煮三分钟,则外面看似热呼呼的不错,但里面却只有60度,这很容易导致微生物未被杀死的危险情况。这就告诉我们为什么微波炊具加热一段时间后,必须搅拌食物,然后再加热,以确保所有食物均匀加热。
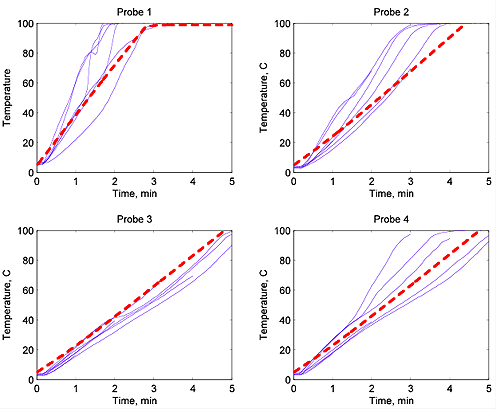 四探针测量食物的温度。蓝线显示实验结果,而红色虚线显示数学预测。
四探针测量食物的温度。蓝线显示实验结果,而红色虚线显示数学预测。 上述预测的准确性表明我们所作出的近似数学模型是合理的。这给了我们信心来使用该模型做很多“假使......将会怎么样”的计算,并据此设计不同的微波炉并评估它们安全煮食的能力。事实证明,搅拌器模式的微波炉比转盘的好,那些有混沌微波频率的最棒。
结论
我只触及数学在食品工业中的重要应用的一些表层。其它应用包括使用统计方法确保食品的质量(正是吉尼斯在统计中首次推出著名的t检验),利用成像方法测试产品的保鲜程度,利用流体力学设计甜食等。传热数学对速冻食品的储存和解冻设施的设计也是非常重要的,它使食物保鲜且安全。食品行业,特别是食品安全,是数学和数学家可以作出重大贡献的一个领域。




