当伟大的数学家艾萨克•牛顿解释彩虹的颜色与折射时，诗人约翰•济慈吓坏了。济慈抱怨（当然通过诗），数学解释打劫了这些魔幻般的“所有规则和线条的奥秘”的自然奇观。但是，正如我们下面将看到的，数学解释只需要基本的几何线条和圆圈，漂亮的数学原理和彩虹本身是一样的优雅。

因折射而弯曲

彩虹的颜色是因光折射而分裂成的一个结果，就像光线通过棱镜照射时所发生的那样。从太阳上来的白光是不同频率电磁波的组合。当这些频率的组合在同一时间到达你的眼睛时，你就能看到白色，当你的眼睛捕捉到其它的波时，你就会感知另一个特定的颜色。

约670至780兆赫频率之间的光波被视为紫罗兰色调，光谱的另一端是波频率在约400至480赫兹之间，它给出了不同深浅的红色知觉。而所有其它颜色均来自这两个频段之间的频率。一般来说，人眼不能感知所有频率的电磁波。

可见光谱从紫色（左）到红色（右）

当一缕阳光碰到一个球形水滴，它的一部分将从液滴的表面反射，但另一部分将进入它。当进入时，光线会弯曲或折射，这是将吸管插进一杯水时看到的同样现象。然后光线将继续行进直到液滴的后部。这时有些光线会离开水滴出去，但有些将被反射回来到液滴的另一边，并在这一过程中再次折射。（见图1）

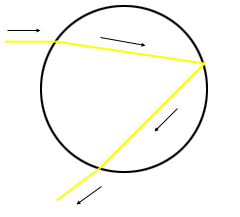图1：一条光线被折射，反射，然后再次折射。

折射是一缕光线从一种介质传递到另一种介质而速度放缓的一个结果。一个非常粗略的类比是想象将一个购物推车以某种角度从路上推向草地：推车因为撞击草地将首先放缓，然后改变方向。

当太阳光通过一个真空（很好的近似是通过空气），所有频率以每秒约30万公里的相同速度$c$行进。当光线入水时，频率不变因而颜色也保持不变。然而，它的速度会改变，其数额取决于频率。这是因为水的原子结构与不同频率的波的相互作用不同。频率为$f$的光的速度放缓的一个度量由折射率$n_{f, w}$给出。它的值不仅取决于频率$f$，也取决于光线进入的介质（在这种情况下，是水，并用下标$w$所示）。该指数被定义为

频率$f$变化时折射率几乎没有变化：$n_{f, w}$在频谱紫罗兰端约为1.34，而在红色端为1.33左右。但这个小变化可以让我们看到在彩虹中所看到的阳光分成颜色漂亮的光谱。（折射率也随温度略有变化，但这里我们可以忽略它。）

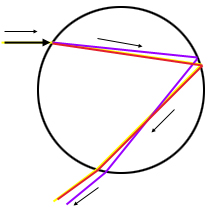图2：不同频率的光有不同的折射

不同频率的光进入液滴弯曲多大由Snell定律描述。该定律说，折射光线位于由入射光线和入射点法线所形成的平面上，法线是通过射线撞击液滴的那点并和液滴表面垂直的那条线。由于我们假设是球形的液滴，在这种情况下，法线是连接液滴中心和入射点的扩展半径。

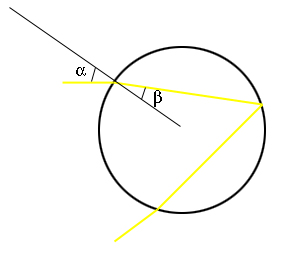图3：包含入射光线和折射光线的水滴的横截面。Snell定律表明角度α和β有关系。

Snell定律也告诉我们，光线折射的角度由下列方程决定：

这里$\alpha$和$\beta$是如图3所示的角度，$n_{f, w}$和$n_{f, a}$是频率为$f$的光分别在空气和水中的折射率。由于空气非常类似真空，它的折射率$n_{f, a}$对所有的频率几乎等于1。因此，如果光线以角度$\alpha = 45^{\circ}$碰到液滴，则折射率为1.33的红光对应的角度$\beta$为

上面的结果四舍五入到小数点后两位。折射率为1.34的紫外线光有

正是这些不同频率的光导致的不同折射角度，给出了彩虹的不同颜色。

捕捉彩虹光

但是，为什么我们看到的颜色形成一个完美的圆弧？要了解彩虹的形状，我们假定来自太阳的光可以看成一束平行光线并射向一个特定的水滴。使用Snell定律和反射律（即入射角等于反射角），我们可以计算出一根射线偏离它第一次进入液滴时的角$\alpha$多少。换句话说，当它被折射、反射，然后再折射后以什么角度转向（见图4）。这个角度当然因不同频率或不同颜色的光而异。

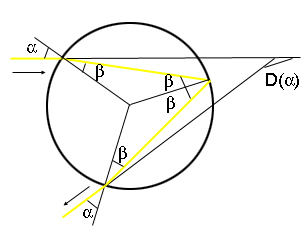图4：算出的角度偏差

多看一眼图4你就会信服自己，偏差$D_f(\alpha)$由下面公式

给出。从Snell定律，我们可以在上式中作替换

这里我们把空气的折射率取为1。图5显示了$D_f(\alpha)$的图像，这里对某一特别选取的红光阴影取折射率$n_{f, w} = 1.33$。注意在$60^{\circ}$左右某个$\alpha_m$处它取一极小值。

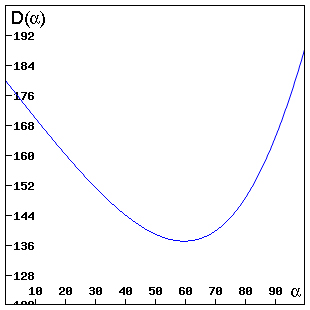图5：DF($\alpha$)的图像

就是这个最小角$\alpha_m$给了我们彩虹。图6显示了液滴的一个包含一束光线的二维断面，折射率为$n_{f, w} = 1.33$。在这个横截面上以最小角$\alpha_m$进入的光线用红色显示，它被称为彩虹线。彩虹线附近的光线（角度接近$\alpha_m$）撞击液滴后，在液滴中行进后，会围绕着彩虹线的附近聚集。所以，如果你的眼睛正好赶上这液滴后端出现的彩虹线，你会看到一大堆的其它射线，使来自液滴的光显得特别强烈。由于所有的聚集光线有相同的颜色，如选取的是具有$n_{f, w} = 1.33$的红光颜色，则液滴在天空中呈现红色。

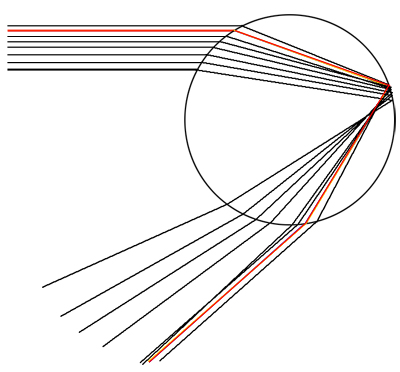图6：图中彩虹线以红色表示。来自水滴的一簇光线在彩虹线周围出现，而其它地方出现的光线则更加分散。

新出现的的红色光线在彩虹线附近聚集这一事实是$\alpha_m$为函数$D_f(\alpha)$的极小点的一个结果。你可以从图7看到这点。取以极小点为中心的一个区间$I_1$以及以其它点为中心具有同样长度的另一区间$I_2$。对应于$I_1$内的值的角度值偏差范围（由区间$J_1$给出）比对应于$I_2$的角度偏差范围（区间$J_2$）小得多。这样，以$I_1$中的角度$\alpha$撞击液滴的光线会非常稠密，而以$I_2$中的角度$\alpha$撞击液滴的光线将相对比较稀疏。

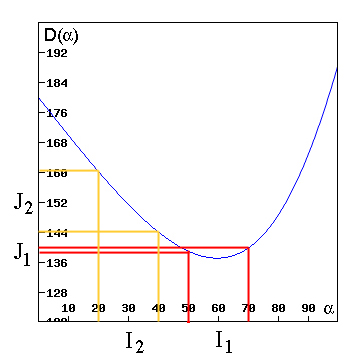图7:区间$J_1$小于区间$J_2$

如果你不相信这张图，这个链接给出一个证明。

色彩锥

很多个液滴形成了天空中的众多红点，由这些你的眼睛就能捕捉到所引出的红色彩虹线。为了看到在天空中的这些液滴相对于你在哪里，让我们先算出$\alpha_m$的精确值。解方程$\dfrac{dD_f(\alpha)}{d\alpha} = 0$找到最小点

（细节可见另一链接）。

对于我们特别选取的红光阴影，代人$n_{f,w} = 1.33$给出$\alpha_m = 59.58^{\circ}$，以及$D_f(\alpha_m) = 137.48^{\circ}$。

现在，如果从一个液滴出现的的一条彩虹线到达你的眼睛，那么这意味着出现的光线与图8所示的直线$L$形成一个角度$r_f = 180^{\circ} - 137.48^{\circ} = 42.52^{\circ}$。这根光线延自于直接通过你眼睛的阳光线（请记住，我们假定来自太阳的光线是平行的）。让我们把$r_f$称为彩虹角。当然，它依赖于频率$f$，因此也依赖于颜色。

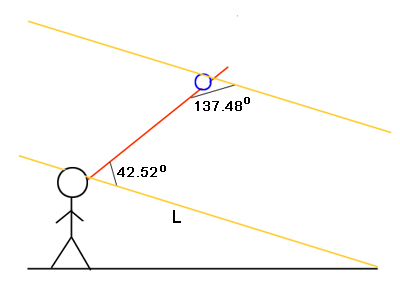图8：由水滴偏离而来的彩虹线与直线L形成了一个42.52度的倾斜角。

如果把你的眼睛发出的所有和$L$相交$42.52^{\circ}$角度的光线放在一起，将得到一个圆锥体（见图9）。所有发出红光的液滴都在此锥上；如果不是的话，你将不可能捕捉到它们的红色彩虹线。但是，当你从锥的顶点沿着锥表面看，所有你看到的都是一个圆。你可以通过将一张纸卷成锥形状并通过尖端的小洞窥视来尝试这点。彩虹来自锥面上与你的眼睛距离不一的水滴，有的较近有的较远。但你的眼睛无法分辨距离，它看到的是红色光混合在一起形成的一个圆弧，似乎是位于有一定距离的某处。为什么你往往看不到完整的圆呢？这是因为地球的缘故。除非你的位置高于天空中的水滴，例如从飞机上俯视，在这种情况下，你可以看到一个美丽的圆形彩虹。

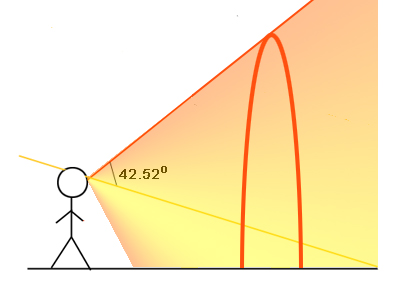图9:你看到的在天空发光的水滴位于一个圆锥体的表面。

同样的道理适用于频谱的所有其它颜色：它们同样以圆弧状出现。但不同的折射指数给予每种颜色不同的彩虹角。例如，紫光的$n_{f, w} = 1.34$给出$\alpha_m = 59.0^{\circ}$及$D_f(\alpha_m) = 138.93^{\circ}$，因而在这一情形彩虹角为$41.07^{\circ}$。因此，彩虹根据折射率顺序来嵌套排列颜色序列，也就是说，按它们的频率顺序排列：从最顶的红色往下直到最底的紫色。

这种解释也说明为什么背朝太阳站着时你只看到一道彩虹：这是你可以捕捉来自于液滴的彩虹光线的唯一途径。这也解释了为什么彩虹下面的天空显出比上面的更明亮。由于绝大多数的光线离开液滴后高于彩虹线（见图6），你不会捕捉到彩虹“上面”来自水滴的任何光线（即位于各种颜色的锥的外面）。所以你看不到任何源自这些水滴的反射光。然而，你的眼睛能捕捉到来自水滴彩虹“下面的”的反射光（位于锥体内的水滴）；鉴于此，彩虹下面的天空显得更亮，它以白光出现，因为从不同的水滴来的不同颜色的非彩虹光线混合在一起会成为白光，并进入你的眼睛。

彩虹几何也表明，任何你看到的彩虹是你的，也仅仅是你的，虽然站在你旁边其他人也会看到彩虹，但它一般会来自不同的水滴，因此这将是一个不同的彩虹。

如果你是幸运的，有时候你可能会在略高于主彩虹处看到暗淡一点的第二个彩虹。这个副虹是水滴内光线两次反射的一个结果。在这种情况下，各种颜色的彩虹角度约为51度，这是为什么副虹在天空看上去高一点的原因。双反射也意味着副虹的颜色以相反的顺序出现，底部为红而顶部为紫。下面是笛卡儿所作的原始草图，他天才地首先解释了彩虹的形状，包括主虹和副虹。与副虹相关的双反射由红线跟踪。

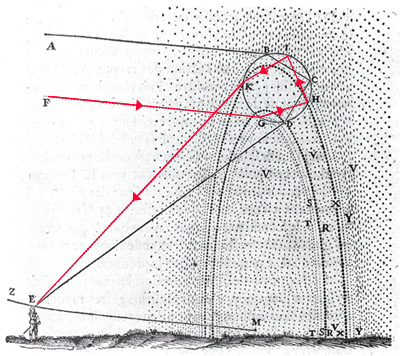笛卡儿的草图：主要和次要的彩虹

甚至有可能在理论上（尽管实际中鲜有发生）看到来自水滴内三、四个或更多的反射产生的彩虹。但我把这些计算留给读者们。