正弦语言
作为一名电子音乐人,我一直被正弦波吸引着,它们曾作为我的第一台穆格电子琴的声音发生器。在节录乐曲成为可能的80年代后期,我了解到,通过傅立叶分析,所有声波都可以被分解成一系列正弦波,分解后的正弦波还可以再重新复原成声波。现今我们听到的来自于数字装置的每一种声音,从HDTV到IPod,在数字范畴上都是通过一系列的正弦波的叠加形成的。
 图1:左图为穆格电子琴发出的纯震动音调的谐波成分。中图为正弦语言:从图片下面的粗白线可以看出,基频大概150赫兹。右图为锯齿波和平方波:都可以产生许多不同的谐波,从而引发不同的声音
图1:左图为穆格电子琴发出的纯震动音调的谐波成分。中图为正弦语言:从图片下面的粗白线可以看出,基频大概150赫兹。右图为锯齿波和平方波:都可以产生许多不同的谐波,从而引发不同的声音 正弦波在自然界中的唯一性在于它们不包含任何除自身的基频以外的谐波,它们从不产生谐波阴影或反射,简直就是声音世界的吸血鬼。
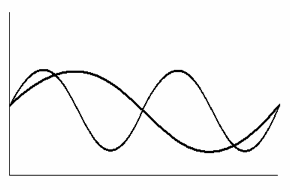 图2:相同振幅的正弦波,频率相差1.5倍
图2:相同振幅的正弦波,频率相差1.5倍 “正弦语言”这段音乐是为奇客流行狂欢节所写。主要探索正弦波的思想以及它与其他概念(比如以平均律著称的西方调律准则,甚至古希腊的宇宙论思想)的联系。(点击这里收听正弦语言)
正弦波因其自身完美的理论而迷人:它们不包括在它固有频率之上的谐波(或者从音乐的角度上讲,音调)。正因如此,多种混合的分别代表特殊音调的正弦波并不能被人耳区分解读,而是听起来像单一的经过音色调节的音调。正弦语言的第一分钟逐一介绍了7种不同的经过调律的正弦波,从低音开始到高音结束。构成音乐前半段的这七种音调被调律成了完全五度。这点很不寻常,因为在钢琴键盘中的五度是不完全的。为了理解其中的原因,我们需要简要地追溯起源于古希腊的西方调律史。
古希腊的宇宙论思想
也许是毕达哥拉斯注意到了铁锤击打铁钻时产生的和谐音符,从而开始思考和谐音之中的数学原理。他进而发现,把一根弦分成两段后弹奏会产生2倍于原来的弦所产生的音符。因此,如果原来的弦一秒钟振动500次(即频率500赫兹),那么剪成一半长度的弦的振动频率将会加倍,也即一秒钟振动1000次(频率1000赫兹)。
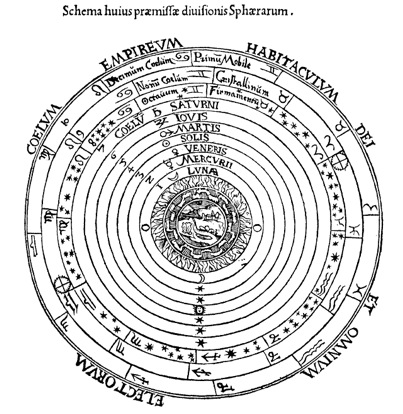 图3:古希腊的宇宙论思想
图3:古希腊的宇宙论思想 从音乐的角度上,这意味着我们听得1000赫兹的音符是2倍的500赫兹的音符,这被称为一个八度。假设你把这两种音符一起弹奏,听起来将非常和谐,因为在500赫兹对应的的音调中的一次振动,你可以适应1000赫兹对应音调的两次振动。我们的耳朵和大脑将此翻译成悦耳的声音——也许是因为人耳可以用较少的受体进行编译,从而传给大脑的听觉神经。
但是,1:2并不是唯一可以被我们的耳朵编译成和谐音的比率。作为大自然赋予我们的众多优雅的惊喜之一,许多其它的整数比率产生的混合音调也能使人悦耳,并且通过引入这些比率,可以建立音节,也就是我们熟知的纯律。
古希腊人对这一简洁的发现印象深刻,并给这个发现赋予了哲学含义,这就是所谓的“天籁之音”。那时,人们坚信宇宙中行星和太阳的轨道都是以地球为中心的完美圆周,这些天体在水晶球的表面沿着各自的轨道运动,它们之间的空间距离服从音程中对应的完美的数学比率,并且其相互间的运动产生了天体的音乐(宇宙的音乐)。虽然人类无法听到这乐曲,它却表达着宇宙的完美。
尽管这个想法非常的优美,但是只使用纯律来分解音节还是有很多问题的,在人们进行了诸多尝试之后,完美的解决方案最终在17世纪的西方被找到。
| 音程(Musical interval) | 比率(Ratio of frequencies) |
| C-D | 9:8 |
| C-E | 5:4 |
| C-F | 4:3 |
| C-G | 3:2 |
| C-A | 5:3 |
| C-B | 15:8 |
| C-C | 2:1 |
| 图4:C大调的音程及其对应的比率 | |
从音乐角度上讲,这些完美的比率只有当保持一种音调时才能成立。从图4中的C大调表格可以看出,所有的音符对于C调都可以完美调律。因此,任意一段音乐,如果想让它和谐悦耳,都需要从C大调开始并以C大调结束。钢琴演奏中为了产生悦耳的音乐,只能使用键盘上的白色音符。因为假设你从D大调开始,那么对于音节中的音符而言所有等价的比率都会完全不同,按音乐术语说,就是恐怖的声音(horrible sounding)。在键盘调律中(使用纯律),就C大调而言,D音符和A音符的频率分别是C音符的9/8倍和5/3倍。但根据纯律准则,高于D调的完美五度应该满足频率为D调的3/2倍,也就是27/16倍C调的频率(3/2乘以9/8);这很接近但并不精确等于键盘A调的频率(C调频率的5/3倍)。在这之后,人们开始引入黑键并试图让它们与这些比率规律相匹配。
另一方面,如一直保持C调并只使用白音符,肯定会令人厌烦的,并且只能创作出有限范围的变音。音乐人大多是冒险主义者,不会满足于之前的框架,自16世纪的西方开始,人们发展了各种允许更多音调转化的调律系统。这种音调间的转化被称作抑扬,发现既可以满足不同音调的抑扬,比如从C到D,又能保证得到的D调听起来悦耳的调律系统是非常困难的。技术上说,这些节外生枝的音符被称作“狼音”,是巴洛克音乐和早期剧作家的毒瘤。
 图5:带有分割黑键的大键琴(大约1620年),可以调律出不同音调的悦耳声音。
图5:带有分割黑键的大键琴(大约1620年),可以调律出不同音调的悦耳声音。 在尝试了众多的解决办法之后(包括把钢琴的黑键进行分割,以便在所弹奏的音调中找到合适的调律方法,见图5),最终的解决方案被称为平均律(十二平均律),这是一个完美的妥协:保持所有比率为2:1的八度,然后对这个音程做平均分割划分音节。这就意味着,虽然所有的音调都有平均而轻微的音错但对所有可能的音调来说却是可以接受的。这和以前的情形正相反,那时,只有一个音调悦耳而其他的音调都有自己独特并可怕的音阶划分。
从数学的角度上说,这意味着12段音节中的任何一个都比它相邻的音节或高或低1/12个八度。为了尊重古希腊“完美和谐”的原创思想,这些偏离于“完美”的音阶通常被称作“毕达哥拉斯音错”。
在平均律出现之前人们熟知的是接近平均律(好律)系统。这两种调律方式的相似之处在于它们都允许在音调之间的抑扬,但是在数学上,它们并不完全等价。例如,17世纪的威克马斯特调律系统(威克马斯特律)涉及五度音和三度音锐化及压缩的变化。尽管这个解决方案并不完美,巴赫还是足以用这一方法写出了48首前奏曲和赋格(《平均律钢琴曲集》),其著作包括了键盘上每个大小调的前奏曲和赋格。在一段乐曲中使用不同的曲调并包含语调中的抑扬,在接近平均律(好律)出现之前是不可能的。
上述信息意味着我们已经习惯于聆听平均律框架下的音乐,而极不适应经过完美调律的声音,甚至认为这种音乐是杂乱无章的。这些信息都和我的作品有联系,为了产生音阶中的第五个音节,我使用了整数比率,从而产生了更接近于希腊和谐音但不是平均律的悦耳音乐。
创作正弦语言
正弦语言的前半部分,是由7种不同正弦波经过调试得到的音符构成:
-
1. 固有频率(基频)– 频率为116.541赫兹的a Bb
2. 2倍的固有频率(高一个八度)
3. 3倍的固有频率(比上一个音符高1/5)
4. 4倍的固有频率(比基频高2个八度)
5. 6倍的固有频率(比上一个音符高1/5)
6. 8倍的固有频率(比基频高3个八度)
7. 12倍的固有频率(比上一个音符高1/5)
我们把基频和一系列整数相乘:每两个相隔的音符都满足二倍关系(从而高一个8度),而他们之间的音符是前一个音符的3/2倍(完全五度)。这是基于多数音乐频繁使用2、3和4整数倍这一事实的一个随意的选择:对音乐的拍号而言,一个小节线中通常有3或4拍,而且音乐的语句通常由4或8个小节组成(对于一段音乐,特别是古典音乐,通常是16、32或64个小节拍)。如果探讨为何2整数倍可以带来和谐悦耳的音乐,则需要另外一篇文章来讨论,或许这仅仅是一个传统习惯?(世界上的其它文化确有使用其它系统的案例)。
前半段音乐中另一个简单的数学思想是使用相同的数学序列来定义节奏。我随心所欲的决定前半段音乐应该致力于创作一个完美的节拍,后一段音乐以这个完美的节拍作为启动并寻求更多自由的组合。这个完美的节拍可以参见图6:
 图6:正弦语言的乐谱:可以看出,从最低部基频开始逐一被引入的7个音符,以及通过音符组成的节奏
图6:正弦语言的乐谱:可以看出,从最低部基频开始逐一被引入的7个音符,以及通过音符组成的节奏 从音乐的角度上讲,这个节拍可以使得三连音和二连音之间更有层次感,是一种在许多音乐中少见的技巧,19世纪晚期的浪漫音乐青睐这种技巧。这个做法虽然会因为加快或减慢音符而打乱音乐的节奏,却可以产生悦耳的音乐。例如,我们可以在通常需要弹奏两个音符的时候弹奏3个音符(被称为三连音),并且恰好适应下一个音符的节拍。虽然这种做法违背了音乐的主要节奏点,但令人颇为惊奇的是它并不会打乱音乐的整体感觉。
我上面所描述的完美节拍,建立了一种悦耳和强劲的声音,听起来有完美的复合度,但很显然,它是由一些独立的元素组成的:你可以在这里收听(重复播放多遍)
在这段复合的舞曲(twist)中,独立的音符和声音流是通过非常规的方式进行调律的,但由于它们都是全音符和整数比率,音乐仍然听起来和谐,当然了,对于经过训练的耳朵而言,也许会有轻微的不习惯。
前半段音乐通过逐渐的给音乐引入划分音节,来建立如前所述的节拍。正弦波被逐一引入,并且逐渐地从轻柔的有起有落的音量转化为从静音到最大音量之间的离散跳跃。这是一种在模糊状态和二进制状态(像开关一样)之间的转化。
图6是前半段音乐的乐谱,呈现了上述转换是如何实现的。然而,它们很难被耳朵分辨,因为人耳习惯于把正弦波融合成混音,以便使你听到细致转化过的悦耳声音,至少使所有的正弦波都达到完美的节拍,还能听到不同的音调。
后半段音乐将这个完美的节拍植入音乐采样器(一种可以把声音加快或减慢到合适频率,并通过任何音调重复播放声音的装置)。这种技术在过去的20年里已经得到普及,我也许并不需要举例说明它如何工作,但这里还是呈现一个被音乐采样器返回的完美的节拍,首先是它的原本的声调,然后是不同的声调,每次都升高一个八度。
 图7:正弦语言乐谱的放大图:呈现了每种音符的波形。很容易分辨出完全五度(3:2)和八度(2:1)的比率。从上面波形可以看出,音符7完成3个周期的时间等于音符6的2个周期时间,同样,音符6的两个周期时间的等于音符4的一个周期。
图7:正弦语言乐谱的放大图:呈现了每种音符的波形。很容易分辨出完全五度(3:2)和八度(2:1)的比率。从上面波形可以看出,音符7完成3个周期的时间等于音符6的2个周期时间,同样,音符6的两个周期时间的等于音符4的一个周期。 后半段音乐更多的是音乐而不是数学,一旦被植入音乐采样器,它就可以像普通的声音(比如钢琴)一样被播放。尽管如此,考虑到声音的自然属性,使用它进行和弦演奏可以产生彼此交织、环环相扣的正弦波网络,这些正弦波是数学角度上令人愉悦的音调,并且这一定不是平均律。(你可以在这里收听整段音乐)
不过,我们知道音乐采样器确实返回基于平均律的声调(因为音乐采样器使用这种调律系统),因此,最终产生的音乐是经过完美调律,是基于平均律音程演奏出来的。所以,这种调律方法极端的复杂,我想可以简单的描述为“毕达哥拉斯平方音错”。
 图8:完美的节拍:显示了每个音符的节奏划分。第一个音符一拍发声一次,第二个音符一拍发声两次,第三个音符一拍发声三次,第四个音符一拍发声四次,第五个音符一拍发声六次,第六个音符一拍发声八次,第七个音符一拍发声十二次。
图8:完美的节拍:显示了每个音符的节奏划分。第一个音符一拍发声一次,第二个音符一拍发声两次,第三个音符一拍发声三次,第四个音符一拍发声四次,第五个音符一拍发声六次,第六个音符一拍发声八次,第七个音符一拍发声十二次。 交错的正弦波及调律的累积效应使我联想起了巴赫创作的风琴曲,那是多么美妙的音乐!虽然很多人不知道音乐背后的框架是数学原理,但读了本文后,您也许能够理解这些看起来抽象的数学确实可以导致近似完美的音乐产物。作为一个职业音乐人,我为数学和音乐的美妙结合感到欣喜!
最后,我想指出,虽然很多人和我一样并不具备巴赫的天才以及他对谐和音的深刻理解,但我们确实得到了同样无与伦比的音乐享受。




