1. 伯努利方程的建立

凡是学过流体力学的人们都知道，在 1738 年瑞士数学世家丹尼尔·伯努利（Daniel Bernoulli ，1700 年～1782 年，如图 1 所示）将质点运动的动能定理运用于同一微元流管的两截面上，导出了表征一元流机械能守恒方程，即著名的理想流体定常流动的能量方程 (后称为伯努利方程)。对于理想不可压缩流体的定常流动，在质量力为重力作用下，沿同一条流线单位重量流体质点所具有的总机械能守恒（单位重量流体质点的位置势能、压强势能和动能之和不变，或总水头为常数）。

$$z+\frac{p}{\gamma}+\frac{V^{2}}{2 g}=H=C$$

其中，$z$ 为流体质点的位置，$p$ 为流体质点的压强，$V$ 为流体质点的速度，$γ$ 为流体容重，$g$ 为重力加速度，$H=C$ 为常数（单位重量流体质点所具有的总机械能，总水头），如图 $2$ 所示。在不计质量力的条件下（空气的质量密度小，可以忽略重力的影响），此时沿同一条流线单位体积流体质点所具有的压强势能和动能之和不变，总压不变）。

$$ p+\rho \frac{V^{2}}{2}=p_{o}=C $$ 其中，$p_0$ 为流体质点的总压，$p$ 为流体质点的静压，$\rho \frac{V^{2}}{2}$ 为流体质点的动压。

图 1 瑞士流体力学家伯努利（Daniel Bernoulli ,1700 年～1782 年）

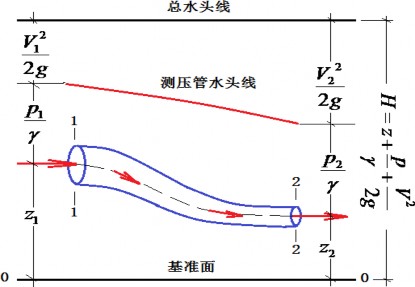图 2 理想流体的伯努利方程几何表示

2. 历史作用与科学贡献

任何理论都是在大量实验研究的基础上发展起来的，流体力学理论的建立也不例外，从历史发展角度看，如果没有大量的流动实验成果，如果没有微积分的出现和连续介质力学，就不会有伯努利方程的建立。可以毫不夸张地说，伯努利方程为人们研究流体运动大开脑洞，起到了里程碑的作用，如果没有伯努利方程不可能将一些貌似不相干的现象用统一理论公式精准表达；如果没有伯努利方程的建立思想，也不可能有后来的表征理想流体微团运动的欧拉方程组；如果没有 Euler 方程组，更不会推广到表征粘性流体微团运动的 Navier-Stokes 方程组（N-S 方程组）。当然，如果没有这些，就不会有流体力学的基本理论。因此，伯努利方程是流体力学的核心方程，起到灵魂的作用。以下通过实例说明之。

1、流体静力学原理

公元前 250 年，受西西里岛叙拉古国王检验皇冠之委托，阿基米

德（Archimedes，古希腊人，公元前 287～公元前 212 年，如图 3 所示）研究了力平衡原理，提出著名的流体力学浮力定理，也是流体静力学的一部分。这个著名的流体浮力原理，在伯努利方程出现之后，人们惊奇地发现它是在静止状态下伯努利方程的精准表达，如图 4 所

示。即

$$ z+\frac{p}{\gamma}=C $$

后来 1653 年，法国科学家帕斯卡（B.Pascal,1623～1662 年，如图 5 所示) 提出了流体静压力传递原理（即帕斯卡定理），并制成了首台水 压机（如图 6 所示），也是利用了静止状态下的伯努利方程。

图 3 古希腊学者阿基米德（Archimedes，公元前 287～公元前 212 年）

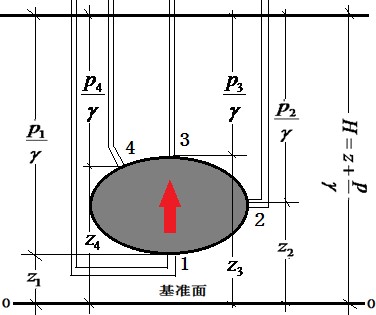图 4 在静止状态下伯努利方程的几何表示

图 5 法国科学家帕斯卡（B.Pascal ，1623～1662 年）

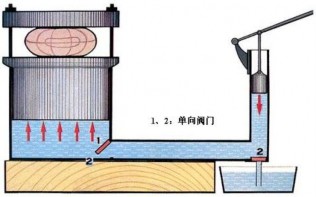图 6 水压机原理

2、定常孔口出流公式

1643 年，意大利科学家托里拆利（E.Torricelli，1608～1647 年）通过大量的孔口出流实验，提出了定常孔口出流的基本公式，表明孔口出流速度与孔口上的水深 $h$ 平方根成正比，如图 5 所示。即

$$ h=\frac{V_{c}^{2}}{2 g}, V_{c}=\sqrt{2 g h} $$

这个方程实际也是伯努利方程在大气压明流下的精确表达形式。其物理意义是，单位重量流体质点 1 所具有的重力势能转变为单位重量流

体质点 2 的动能。

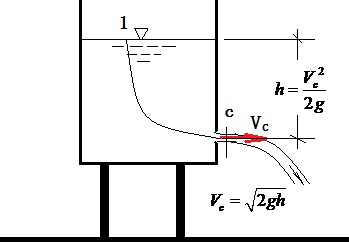图 7 在大气压出流条件下的伯努利方程表示

3、皮托管测速仪

1732 年，法国水力工程师毕托（Henri Pitot，1695～1771 年) 发明了一种测量流体中总压的装置，即皮托管（如图 6 所示，也有叫毕托管）。皮托发现河流中的水柱高度正比于皮托管入口水深处流速的平方，水流中任意一点的速度大小，可以对同一点分别用总压管和静压管的测量值之差获得。后来 1905 年世界流体力学大师普朗特（Ludwig Prandtl，1875～1953，如图 7 所示）将这一方法发展成为同时测量流体总压和静压的装置，提出了普朗特风速管，也叫皮托管测速仪（如图 8 所示）。皮托管测速原理，也是伯努利方程的精确表达，表明流体质点的动压等于同一点流体质点的总压与静压之差。

$$ \rho \frac{V_{0}^{2}}{2}=p_{o}-p_{s}, V_{0}=\sqrt{\frac{2\left(p_{0}-p_{s}\right)}{\rho}} $$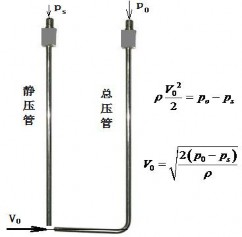

图 8 毕托总压管（伯努利方程应用）

图 9  德国力学家、世界流体力学大师路德维希. 普朗特（Ludwig Prandtl，1875～1953 年）

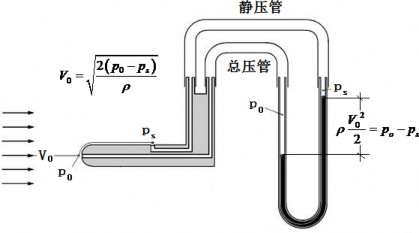图 10 普朗特风速管（皮托管测速仪）

4、文丘里流量计与一元管流理论

1797 年意大利物理学家文丘里（G.B.Venturi,1746～1822 年，如图 9 所示）通过对变截面管道实验，发现最小截面处速度增大、压强减小（文丘里效应），提出利用这一效应和连续条件测量管道流体流量的收缩扩张型管道，即文丘里管（如图 10 所示）。其基本原理（如图 11 所示）是：对于通过理想不可压缩流体的水平管道，如果在管道中插入一段先收缩后扩张的管段，根据文丘里效应，建立管道收缩前 1 断面和收缩后 2 断面之间的伯努利方程，并利用连续性条件，可得管道通过的体积流量 Q。即

$$ \begin{array}{c}{p_{1}+\rho \frac{V_{1}^{2}}{2}=p_{2}+\rho \frac{V_{2}^{2}}{2}, Q=V_{1} A_{1}=V_{2} A_{2}} \\ {Q=V_{1} A_{1}=A_{1} \sqrt{\frac{2}{\rho} \frac{\left(p_{1}-p_{2}\right)}{A_{2}^{2}}-1}}\end{array} $$

以后所发展的一元管流和明渠流理论都是基于一元流伯努利方程和连续方程得到的。

图 11 意大利物理学家文丘里（G.B.Venturi,1746～1822 年）

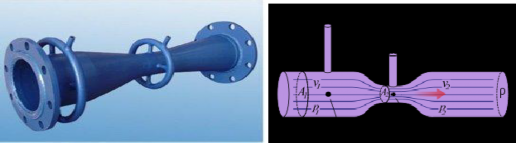图 12 文丘里流量管

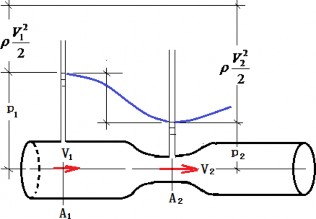图 13 文丘里流量计原理（伯努利方程在管流中的应用）

5、翼型绕流升力原理

1687 年，英国科学家牛顿 (Isaac Newton，1642 年～1727 年，如图 12 所示) 在其著的《自然哲学之数学原理》中首次定量给出作用于翼型上的升力和阻力表达式。即

$$ L=\frac{1}{2} \rho V_{\infty}^{2} b C_{L}, D=\frac{1}{2} \rho V_{\infty}^{2} b C_{D} $$

其中，$L$ 和 $D$ 为升力和阻力，$V_∞$ 为飞行速度，$b$ 为机翼面积，$C_L$ 和    $C_D$ 为升力系数和阻力系数，$ρ$ 为空气的密度。牛顿认为：在空气中运动物体所受的力，正比于物体运动速度的平方和物体的特征面积以及空气的密度。牛顿根据作用力与反作用力原理，提出所谓的“漂石理论”（Skipping Stone Theory），认为翼型所受的升力是翼型下翼面对气流的顶托作用的结果，与上翼面无关（如图 13 所示），风洞实验表明下翼面顶托作用所产生的升力只占总升力的 30%。

图 14 英国科学家牛顿（Isaac Newton，1643～1727 年）

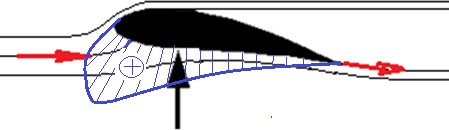图 15 牛顿的漂石理论（下翼面的顶托作用）

1738 年伯努利提出理想流体能量方程式后，为正确认识翼型升力提供了理论基础，特别是由能量定理得出，翼型所受的升力大小不仅与下翼面作用的空气顶托力有关，也与上翼面的吸力有关（如图 14 所示），后来的风洞实验证实，这个上翼面吸力约占翼型总升力的 70%。在翼型绕流中，由连续性条件，绕过上翼面的空气速度大于来流速度，根据伯努利方程得出上翼面的压强小于大气压强，因此上翼面将受到周围空气的吸力，由此会产生向上的升力，致使翼型绕流产生的升力得到较为完美的解释。即翼面上的压强系数为

$$ C_{p}=\frac{p-p_{\infty}}{\frac{1}{2} \rho V_{\infty}^{2}}=1-\left(\frac{V}{V_{\infty}}\right)^{2} $$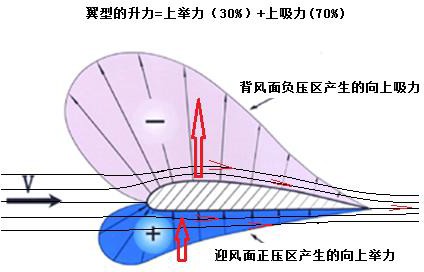

图 16 翼型压力分布及其对升力的贡献

6、理想流体运动微分方程组（Euler 方程组）

瑞士数学家与流体力学家欧拉（Leonhard Euler,1707 年～1783 年，如图 15 所示），师从瑞士数学家约翰·伯努利（Johann Bernoulli，1667～1748 年），约翰·伯努利为丹尼尔·伯努利的父亲，后来跟随丹尼尔·伯努利研究流体力学。1753 年欧拉提出了连续介质假设，1755 年提出描述流体运动的空间点法即欧拉方法，并基于连续介质假设和理想流体模型，依据伯努利建立能量守恒方程的思想，利用动量守恒定理建立了理想流体运动的微分方程组。即著名的欧拉方程组。

$$ \begin{aligned} \frac{d u}{d t}&=\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z}=f_{x}-\frac{1}{\rho} \frac{\partial p}{\partial x}\\ \frac{d v}{d t}&=\frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}+w \frac{\partial v}{\partial z}=f_{y}-\frac{1}{\rho} \frac{\partial p}{\partial y}\\ \frac{d w}{d t}&=\frac{\partial w}{\partial t}+u \frac{\partial w}{\partial x}+v \frac{\partial w}{\partial y}+w \frac{\partial w}{\partial z}=f_{z}-\frac{1}{\rho} \frac{\partial p}{\partial z} \end{aligned} $$

其中，$u$，$v$，$w$ 分别为质点的速度分量；$f_x$, $f_y$, $f_z$ 分别为作用于质点上的单位质量力；$p$ 为质点速度。该微分方程组清楚地表明，改变流体微团运动行为的是作用于微团上的质量力和微团表面上的压强力。也就是说，如果不考虑质量力，沿着某个方向无压力梯度，则沿该方向流体质点的速度保持不变。写成矢量形式为

$$ \frac{d \vec{V}}{d t}=\vec{f}-\frac{1}{\rho} \nabla p $$

对于质量力有势、理想不可压缩流体的定常流动，沿着流线积分欧拉方程组，可得到伯努利方程。进一步研究表明，不仅沿着同一条流线满足伯努利方程，沿着同一条涡线、势流流场、螺旋流均满足伯努利方程。可见，欧拉方程组的积分，进一步推广了伯努利方程的适用性。

图 17 瑞士数学家与流体力学家欧拉（Leonhard Euler ,1707 年～1783 年）

7、粘性流体运动微分方程组（Navier-Stokes 方程组）

基于理想流体运动的欧拉方程组，无法给出圆柱绕流的阻力，为此人们急需要研究粘性流体流动问题。经过 1822 年法国工程师纳维（Claude-Louis Navier，1785〜1836 年，如图 16 所示）、1829 年法国科学家泊松 (Simeon-Denis Poisson 1781～1840 年，如图 17 所示)、1843 年法国流体力学家圣维南（Adhémar Jean Claude Barré de Saint-Venant ，1797～1886 年，如图 18 所示），最后由 1845 年英国科学家斯托克斯 (George Gabriel Stokes，1819～1903 年，如图 19 所示) 在剑桥大学三一学院提出应力变形率的三大关系，完成了牛顿流体粘性运动微分方程组的推导，即著名的纳维-斯托克斯（Navier-Stokes）方程组，简称 N-S 方程组。即

$$ \begin{aligned} \frac{d u}{d t}&=\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z}=f_{x}-\frac{1}{\rho} \frac{\partial p}{\partial x}+\nu \Delta u \\ \frac{d v}{d t}&=\frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}+w \frac{\partial v}{\partial z}=f_{y}-\frac{1}{\rho} \frac{\partial p}{\partial y}+\nu \Delta v\\ \frac{d w}{d t}&=\frac{\partial w}{\partial t}+u \frac{\partial w}{\partial x}+v \frac{\partial w}{\partial y}+w \frac{\partial w}{\partial z}=f_{z}-\frac{1}{\rho} \frac{\partial p}{\partial z}+\nu \Delta w \end{aligned} $$

其中，$u$,$v$,$w$ 分别为质点的速度分量；$f_x$, $f_y$, $f_z$ 分别为作用于质点上的单位质量力；$p$ 为作用于质点上的压强；$\nu$ 为流体运动粘性系数；

$△$ 为拉普拉斯算子。写成矢量形式为

$$ \frac{d \vec{V}}{d t}=\vec{f}-\frac{1}{\rho} \nabla p+\nu \Delta \vec{V} $$

这个方程组表明，导致流体微团加速度变化的是作用于流体微团上的

质量力、压强差力（表面法向力）和粘性力（表面切向力，反映在运动方程中表现为动量的粘性扩散行为）。

至此，从 1755 年欧拉导出的理想流体运动方程组到 1845 年建立的粘性流体运动的 N-S 方程组，历时 90 年，数学家们为流体力学基础理论的建立做出了卓越贡献。对于质量力只有重力、不可压缩粘性流体的定常流动，沿着流线积分 N-S 方程组，可得到类似于理想流体的伯努利方程，但在能量方程中多了一项因克服粘性摩擦力做功而损失的机械能项。即

$$ z_{1}+\frac{p_{1}}{\gamma}+\frac{V_{1}^{2}}{2 g}=z_{2}+\frac{p_{2}}{\gamma}+\frac{V_{2}^{2}}{2 g}+\Delta h_{f 1-2} $$ $$ \Delta h_{f 1-2}=\int_{1}^{2} \frac{v}{g}[-\Delta u d x-\Delta v d y-\Delta w d z] $$

与理想流体伯努利方程相比，上式右边多出的项表示单位重量流体质点克服粘性应力做功所消耗的机械能，这一项不可能再被流体质点机械运动所利用，故称其为单位重量流体质点的机械能损失，这个损失与积分路径（流线的形状）有关。这个表征粘性流体流动的伯努利方程表明：在粘性流体中，沿同一条流线上单位重量流体质点所具有的机械能沿着流动方向总是减小的（如图 20 所示），不可能保持守恒（理想流体流动时，总机械能保持守恒，无机械能损失），流体总是从机械能大的地方流向机械能小的地方。

图 18  法国力学家纳维（Claude-Louis Navier，1785〜1836 年）

图 19 法国科学家泊松 (Simeon-Denis Poisson 1781～1840 年)

图 20  法国力学家圣维南（Adhémar Jean Claude Barré de Saint-Venant 1797～1886 年）

图 21  英国力学家与数学家斯托克斯（George Gabriel Stokes，1819～1903 年）

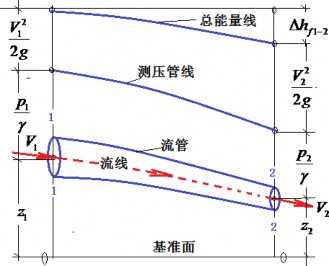图 22 粘性流体运动的伯努利方程

作者简介:

刘沛清，北京航空航天大学陆士嘉实验室