数$1$可以写成单位分数之和，即分子为$1$的分数之和。例如，

$$1 = \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{6}.$$

两边同乘以$6$，得到

$$6 = 3 + 2 + 1,$$

这就证明前一等式成立。

这样的分数分解最多可以含多少项，前提是没有重复的单位分数？大约二十年前我就开始思考这个问题。我决定只考虑分母只有两位数的单位分数，换句话说，分母不大于$99$。

从完美数开始

一个自然数$m$称为完美数，如果它的因子（包括$1$，但不包括$m$）的总和等于本身。作为一个例子，$6$是一个完美数（如你可以在上面看到）。$28$也是，其因子为$14$，$7$，$4$，$2$和$1$，且满足

$$28 = 14 + 7 + 4 + 2 + 1.$$

等式两边除以$28$产生一个有五项单位分数的单位分解：

$$1 = \dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{7} + \dfrac{1}{14} + \dfrac{1}{28}.$$

有许多其他的完美数（例如，$496$，$8128$，$33550336$，$8589869056$）。虽然我们同样可以如上法分解这些数，但每一个分母必须是小于或等于$99$的条件限制了可用数的范围。例如$496$就不行，因为它的两个因子有三位：

$$496 = 248 + 124 + 62 + 31 + 16 + 8 + 4 + 2 + 1.$$

因此，让我们把完美数放在一边，并采取另一种方法。显然，我们可以通过把每个单位分数分解成单位分数之和的方式使得$1$的单位分数的和式加长。例如，

$$\dfrac{1}{3}= \dfrac{1}{4} + \dfrac{1}{12},~~~ \dfrac{1}{6} = \dfrac{1}{7} + \dfrac{1}{42}.$$

下面我们把分解方法推广成五个规则。

规则$1$：分解成两项

让我们看看一个单位分数$1/n$如何被分解成两个不同的单位分数。假设单位分数的分母$n$可以分解成$a$乘以$b$，其中$a$和$b$可以为$1$。这样就可以分解成两个单位分数如下：

$$\dfrac{1}{n} = \dfrac{1}{a \cdot b} = \dfrac{a+b}{(a+b)a \cdot b} = \dfrac{1} {(a+b)b} + \dfrac{1}{(a+b)a}.$$

例如，对于单位分数$1/30$，我们有$n=30$，它可以被分解为$30=5$×6。因此，

$$\begin{array}{} a + b = 5 + 6 = 11 \\ a \times (a + b) = 55, ~~ b \times (a + b)=66 \\ \dfrac{1}{30} = \dfrac{1}{11 \times 6} + \dfrac{1}{11 \times 5} = \dfrac{1}{66} + \dfrac{1}{55} \end{array}$$

我们可以重复这个以创建尽可能多的分解。这样对$1/3$和$1/6$做的结果是

$$\begin{array}{} \dfrac{1}{3} = \dfrac{1}{4 \times 1} + \dfrac{1}{4 \times 3} = \dfrac{1}{4} + \dfrac{1}{12}, \\ \dfrac{1}{6} = \dfrac{1}{7 \times 1} + \dfrac{1}{7 \times 6} = \dfrac{1}{7} + \dfrac{1}{42}. \end{array}$$

用手工这样做相对简单，但也可以使用软件以加快过程。

规则$2$：分解成$n$项

单位分数$1/a$的分母乘上$n$则将此单位分数分解为$n$个分母为$n$×a的单位分数之和：

$$\dfrac{1}{a} = \dfrac{1}{n \times a} + \dfrac{1}{n \times a} + \cdots + \dfrac{1}{n \times a}.$$

用$n=2$和$n=3$的例子就有

$$\dfrac{1}{4} = \dfrac{1}{8} + \dfrac{1}{8}, ~~ \dfrac{1}{8} = \dfrac{1}{24} + \dfrac{1}{24} + \dfrac{1}{24}.$$

规则$3$：用另一法分解成两项

在$1/a$按标准方法分解为两项后，每项单位分数的分母乘上$n$，形成一个$1/(n$×a)的分解。

$$\begin{array}{} \dfrac{1}{a} = \dfrac{1}{b} + \dfrac{1}{c}, \\ \dfrac{1}{n \times a} = \dfrac{1}{n \times b} + \dfrac{1}{n \times c}. \end{array}$$

例如，

$$\begin{array}{} \dfrac{1}{4} = \dfrac{1}{5} + \dfrac{1}{20}, \\ \dfrac{1}{8} = \dfrac{1}{2 \times 4} = \dfrac{1}{2 \times 5} + \dfrac{1}{2 \times 20} = \dfrac{1}{10} + \dfrac{1}{40}. \end{array}$$

规则$4$：分解成三项

现在让我们考虑如何将一个单位分数分解成三项。这样做的关键是找到三个数$a$，$b$，$c$，使得它们的最小公倍数是分母$m$。然后，我们将它们的和$a+b+c$乘到原单位分数的分子和分母上。

$$\begin{array}{} \dfrac{1}{m}  = \dfrac{a+b+c}{m \times(a+b+c)} \\  = \dfrac{a}{m \times(a+b+c)} + \dfrac{b}{m \times(a+b+c)} + \dfrac{c}{m \times(a+b+c)}. \end{array}$$

因为$a$，$b$，$c$的最小公倍数是$m$，我们知道它们中的每一个都能整除$m$。换言之，$a/m$，$b/m$，$c/m$都为单位分数，它们被$a+b+c$除后还将是单位分数。

让我们取$1/12$为例。以$12$作为最小公倍数的三个数是$3$，$4$，$6$，其和为$3+4+6=13$。我们因此于$1/12$的分子分母各乘上$3+4+6$，由上面的公式我们有：

$$\begin{array}{} \dfrac{1}{12}  = \dfrac{3+4+6}{12 \times(3+4+6)} = \dfrac{3}{12 \times 13} + \dfrac{4}{12 \times 13} + \dfrac{6}{12 \times 13} \\  = \dfrac{1}{52} + \dfrac{1}{39} + \dfrac{1}{26}. \end{array}$$

另三个以$12$作为最小公倍数的数是$2$，$4$，$6$。这时和为$2+4+6=12$。所以同理可得到：

$$\dfrac{1}{12} = \dfrac{1}{72} + \dfrac{1}{36} + \dfrac{1}{24}.$$

规则$5$：两项组成一项

偶尔在构造单位分数和时，有时可用一个有更多可能性的单位分数来取代现有的两个单位分数。例如，给出两项分解

$$\dfrac{1}{15} = \dfrac{1}{18} + \dfrac{1}{90}$$

我们可以通过对调左右边来产生一个两项组合

$$\dfrac{1}{18} + \dfrac{1}{90} = \dfrac{1}{15}$$

使用这五条规则，我发现了$1$的$42$项不同单位分数的分解。本文的后面你可以看到它。

两三项的重复分解和组成以找到越来越长的总和等于$1$的式子是打发时间的一个很好方式。但是我们能走多远？一点点积分知识告诉我们最高项数必须不超过$62$。（如果你不熟悉微积分，可以跳过这一节。）

最多$62$项

我们将比较单位分数的和与函数$f(x)=1/x$的积分。下图显示在$x=1$和$x=n$之间的函数（这里我们取$n$为大于$1$的自然数）。显然，图中所示的矩形区域的总和比这两点间的曲线和$x$轴，$x=1$，$x=n$所组成的曲边矩形的面积较大。

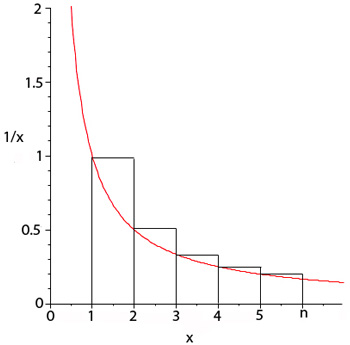
每个矩形水平边长$1$。第一个矩形的垂直边长$f(1)=1$，第二个矩形的垂直边长$f(2)=1/2$，第三个矩形的垂直边长$f(3)=1/3$。继续下去，我们看到第$i$个矩形的垂直边长$f(i)=1/i$。总共有$n-1$个矩形。

因而，这些矩形的面积和为

$$1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{n-1}. $$

将它与等于$f(x)$在$x=1$和$x=n$之间的积分的在$x=1$和$x=n$之间曲线下的面积比较，就有

$$\int _ { 1 } ^ { n } \frac { 1 } { x } d x < 1 + \frac { 1 } { 2 } + \frac { 1 } { 3 } + \ldots + \frac { 1 } { n - 1 }$$

下图显示同样的曲线，这一次画的矩形面积总和小于曲线下的面积。

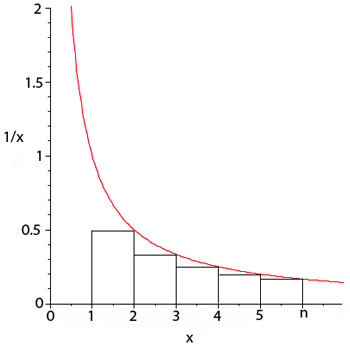
这里第$i$个矩形的垂直边长$1/(i+1)$，故面积之和为

$$\dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{n}. $$

这给出

$$ \frac { 1 } { 2 } + \frac { 1 } { 3 } + \ldots + \frac { 1 } { n } < \int _ { 1 } ^ { n } \frac { 1 } { x } d x$$

将上面的两个不等式合并就有

$$\frac { 1 } { 2 } + \frac { 1 } { 3 } + \ldots + \frac { 1 } { n } < \int _ { 1 } ^ { n } \frac { 1 } { x } d x < 1 + \frac { 1 } { 2 } + \frac { 1 } { 3 } + \ldots + \frac { 1 } { n - 1 }\tag{1}$$

简单推理可得出：

$$ \int _ { 1 } ^ { n } \frac { 1 } { x } d x + \frac { 1 } { n } < 1 + \frac { 1 } { 2 } + \ldots + \frac { 1 } { n } < \int _ { 1 } ^ { n } \frac { 1 } { x } d x + 1 $$

因为上面的积分值为$\log n$，我们有

$$\log n + \frac { 1 } { n } < 1 + \frac { 1 } { 2 } + \ldots + \frac { 1 } { n } < \log n + 1$$

假如我们想要产生尽可能长但不大于$1$的单位分数和，最好使用大分母的分数：分母越大，分数越小，在到达和为$1$之前就能加上更多的项。因此我们不再注视从$1$到$1/n$的和，而是让我们看看从$1/n$到$1/99$的和：

$$\dfrac{1}{n} + \dfrac{1}{n+1} + \cdots + \dfrac{1}{99}.$$

然后我们看在和变得大于$1$之前$n$能取多小。

上面用来构造不等式的论点在把积分上下限从$x=1$和$x=n$变为$x=n$和$x=99$时同样有效。这仅仅是把图形沿$x$轴平移一下。

与前面的不等式类似，我们可以有：

$$\frac { 1 } { n + 1 } + \ldots + \frac { 1 } { 99 } < \int _ { n } ^ { 99 } \frac { 1 } { x } d x < \frac { 1 } { n } + \frac { 1 } { n + 1 } + \ldots + \frac { 1 } { 98 }$$

同样我们可以从上式得到：

$$\int _ { n } ^ { 99 } \frac { 1 } { x } d x + \frac { 1 } { 99 } < \frac { 1 } { n } + \frac { 1 } { n + 1 } + \ldots + \frac { 1 } { 99 } < \int _ { n } ^ { 99 } \frac { 1 } { x } d x + \frac { 1 } { n }$$

求出积分后给出

$$\log 99 - \log n + \frac { 1 } { 99 } < \frac { 1 } { n } + \frac { 1 } { n + 1 } + \ldots + \frac { 1 } { 99 } < \log 99 - \log n + \frac { 1 } { n }$$

右端的不等式告诉我们，为了使得单位分数的和不超过$1$，我们必须有

$$\log 99 - \log n + \frac { 1 } { n } \leq 1 $$

解出$n$得到$n≥8$。这给出和

$$S_1 = \dfrac{1}{38} + \dfrac{1}{39} + \cdots + \dfrac{1}{98} + \dfrac{1}{99} \approx 0.976, $$

它有$99-38+1=62$项。

现在，任何有$63$或更多项的和至少要和数

$$S_2 = \dfrac{1}{37} + S_1 $$

一样大，因为$S_2$牵涉到只有两位数分母的最小的单位分数。如我们已看到，$S_2$大于$1$，这意味着任何$63$项和都大于$1$。特别，任何加起来等于$1$的和最多只能有$62$项。我已经发现一个有$42$项的分解，因而最大项数$62$听起来很合理。

42项解的树图

我目前有$42$项不同单位分数的解看起来是这样的：

$$\begin{array}{} 1  = \dfrac{1}{15} + \dfrac{1}{17} + \dfrac{1}{20} + \dfrac{1}{21} + \dfrac{1}{22} + \dfrac{1}{26} + \dfrac{1}{27} + \dfrac{1}{30} + \dfrac{1}{32} + \dfrac{1}{33} + \dfrac{1}{34} \\  + \dfrac{1}{35} + \dfrac{1}{36} + \dfrac{1}{38} + \dfrac{1}{39} + \dfrac{1}{40} + \dfrac{1}{42} + \dfrac{1}{44} + \dfrac{1}{45} + \dfrac{1}{48} + \dfrac{1}{50} + \dfrac{1}{52} \\  + \dfrac{1}{54} + \dfrac{1}{55} + \dfrac{1}{56} + \dfrac{1}{60} + \dfrac{1}{63} + \dfrac{1}{66} + \dfrac{1}{70} + \dfrac{1}{75} + \dfrac{1}{76} + \dfrac{1}{77} + \dfrac{1}{78} \\  + \dfrac{1}{80} + \dfrac{1}{84} + \dfrac{1}{85} + \dfrac{1}{88} + \dfrac{1}{90} + \dfrac{1}{91} + \dfrac{1}{95} + \dfrac{1}{96} + \dfrac{1}{99} \end{array}$$

取代

$$\dfrac{1}{15} + \dfrac{1}{30} + \dfrac{1}{90} = \dfrac{1}{18} + \dfrac{1}{24} + \dfrac{1}{72}$$

给出另一个$42$项的答案。

下图显示了作为一个树图的解，其中主干是我们的原始值$1$，树枝表明分解为$2$或$3$项的过程。42片叶子中的每一片是解中唯一对应的单位分数项。

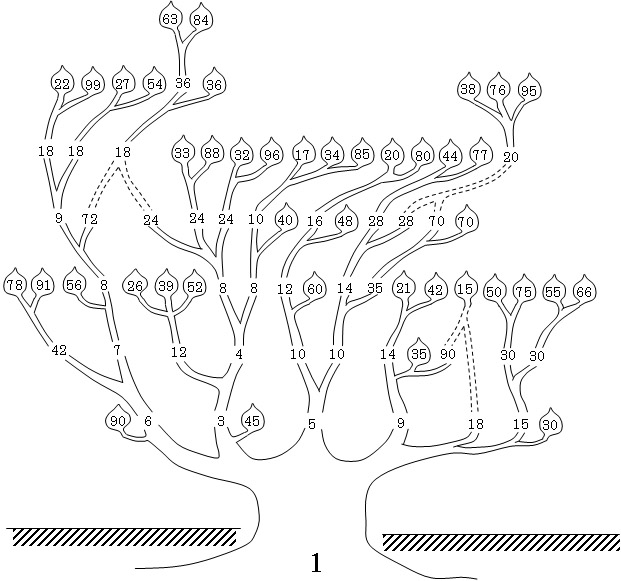
我喜欢这样的图形，但植物学家可能会对浮动树枝感到不安（虚线连接）。这些虚线来自根据规则$5$用一个单位分数取代两个单位分数的组合过程。我在这些过程中执行了：

$$ \dfrac{1}{90} + \dfrac{1}{18} = \dfrac{1}{15}, ~~ \dfrac{1}{72} + \dfrac{1}{24} = \dfrac{1}{18}, ~~ \dfrac{1}{28} + \dfrac{1}{70} = \dfrac{1}{20}.$$

或许更多一点的搜索可消除组合的需要，来修补这些虚线链接。