闲话数学与音乐
蒋迅
1. 引言
数学作为一个工具,真可以说是无所不及,数学和音乐也存在著千丝万缕的联系。德国古典哲学家康德说过,“在任何特定的理论中,只有其中包含数学的部分才是真正的科学”。俄国作曲家指挥家和钢琴家斯特拉文斯基则更是指出,“音乐家应该懂得,对数学的研究就象一个诗人学习另外一种语言一样有用”。爱因斯坦也说过:“这个世界可以由音乐的音符组成,也可由数学的公式组成。”可见数学和音乐的是密切相关联的。
笔者根据网上收集的一些资料加以整理,通过一些初等的数学推导来解释音乐中的一些理论问题并兼谈数学在音乐上的应用,从而说明数学在音乐发展中的重要地位。第 2 节里我们从古希腊数学家对音乐的研究出发,延伸到现代的偏微分方程;然后在第 3 节里用数学方法推导出著名的十二平均律并说明它是最佳的律制;第 4 节我们用对数螺旋线再次说明数学与音乐的关系;第 5 节讨论黄金分割和斐波那契序列在音乐中的应用。
2. 从古希腊数学家对音乐的认识到弦振动方程
音乐发展和数学发展相结合可以追述到古希腊时期。有这样一个古希腊大数学家毕达哥拉斯发现音乐和声的基本原理的故事:他在一个铁匠铺里认识到那些彼此间音调和谐的锤子有一种简单的数学关系——它们的质量彼此之间成简单比,或者说简分数。就是说,那些重量等於某一把锤子重量的 $1/2$,$1/3$ 或 $1/4$ 的锤子都能产生和谐的声响。另一方面,那把和任何别的锤子一起敲打时发出噪声的锤子,它的重量和别的锤子的重量之间不存在简比关系。以他的名字命名的毕达哥拉斯学派认为世界是严整的宇宙,整个天体就是和谐与数。正是这个学派在研究音乐时最早使用了数学(他们试图提出一个声调对比关系的数学公式:八度音与基本音调之比为 $1:2$,五度音等於 $2:3$,四度音等於 $3:4$ 等等),这也是人们最早用数学方法研究美的实践与创始。从毕达格拉斯的发现发展起来的音乐律制称为“自然律制”。
毕达哥拉斯的发现开创了用数学研究音乐的历史。我们知道,声音是空气分子运动的结果。乐器发出声音大多是靠弦(或膜)的振动产生的有规则的空气运动来实现的。人们早就注意到,每一根弦都有它的固有频率。当这根弦缩短一半的时候,它的频率增加一倍。为简单起见,考虑一个两端固定的弦(细长的弹性物质)。应用牛顿第二定律 $F=ma$,我们可以推导出,当这个弦发生振动的时候,它上面每一个点 $y=y(x,t)$ 的运动轨迹(位移)满足弦振动方程:
$$c ^ { 2 } \left(\frac{d ^ { 2 } y}{d x ^ { 2 } }\right) = \frac{d ^ { 2 } y}{d t ^ { 2 }},$$其中 c 是弦振动的波速,t 是时间。这个方程是法国物理学家、数学家和天文学家达朗贝尔 (JeanLe Rond d'Alembert,1717-1783) 于 1747 年建立起来的。这也是历史上第一个偏微分方程。顺便提一句,弦振动频率的计算也是由数学家得到的。英国数学家泰勒 (Brook Taylor,1685-1731) 给出:
$$频率= \frac{1}{2 l} \sqrt { T / \rho},$$其中 $l$ 是弦的长度,$T$ 为弦的张紧程度,$ρ$ 为弦的密度。弦振动方程的建立和求解超出了本文的范围,有兴趣的读者可以参阅上海音乐学院杨健的《走进琴弦的世界──谈近三千年来人类对琴弦的研究及引发的思考》中的附录《拨弦模型的建立、求解和分析》(《自然杂志》2004,26(3):177-183)。在这里我们只能告诉读者,这个方程的通解用数学函数表达就是正弦函数 $p(t)=A\sin(Bt+C)$ 和余弦函数 $q(t)=A\cos(Bt+C)$ 的线性组合。其中 $A$、$B$ 和 $C$ 是一些常数。$C$ 关系不大,而 $A$ 与声量大小成正比,$B$ 与频率成正比。这个线性组合可能是无限的,数学上就是级数求和。因为是三角函数构成的级数,我们称之为三角级数。
3. 从三角函数的周期性看十二平均律
由上一节的讨论我们知道, 三角函数的线性组合是弦振动方程的解。由於余弦函数可以用正弦函数来表示,我们在下面的讨论中不妨假定弦振动的轨迹为正弦函数。当然声音的结果可以是音乐,也可以是噪音。那么我们是如何把音乐和噪音区分开的呢?毕达哥拉斯告诉我们,一个单独的音响无所谓动听与否,而判断一连串声音是不是会让人觉得是噪音关键在於这一连串声音是否和谐。这里的奥妙就在於音符的确定。大家知道,音乐的乐谱是由在不同高度上的多、来、米、发、所、拉、西组成的。从一个多到下一个多经过八个音符。那么这个八度音是如何得到的呢?让我们用数学的方法根据毕达哥拉斯的发现找出八度音里的基本音符。首先,我们先任意确定第一个音符,记作 C。为简单起见,假定它的频率是 1Hz,音量为 1。於是它的数学表达式为
$$y = \sin ( 2 \pi t ).$$确定了 C 之后,我们来选择第二个与 C“和谐”的音符,这就是下一个八度音 C': 它的频率是 C 的两倍: 2Hz,音量也为 1。它的数学表达式为
$$y = \sin ( 4 \pi t )$$从数学图像上看,C 的曲线每秒钟重复一次,而 C' 的曲线每秒钟重复两次。因为它们在第一秒钟的时候都回到 $t$ 轴上 (即 $y$ 值变到零),所以它们产生的音响是和谐的。再下一个八音符 C“的频率应为 4Hz (即 C' 的两倍),所以在 C' 和 C”之间,我们应该加入一个 3Hz 的音符。为了和谐起见,我们必须再加入一个它的频率的一半的音符,这就是在 C 和 C' 之间的第一个八音区里的音符 G,它的频率为 3/2。自然,我们还应该加入一个频率为 5Hz 的音符。这个音符在我们加入的第三个八音符外面。为了在第一个八音区里加入和谐音符,我们必须两次取 5Hz 的一半,於是得到 5/4Hz,这就是在 C 和 C' 之间的第一个八音区里的音符 E。将我们现在已经得到的音符汇总起来,我们得到下面的表格 (C" 以上的音符省略):
| 频率 | 1 | 5/4 | 3/2 | 2 | 3 | 4 | |||||||||
| 音符 | C | E | G | C' | C" |
从上面的表格看,我们不难想到还应该加入一个频率为 5/3Hz 的音符,即 A。於是表格变成:
| 频率 | 1 | 5/4 | 3/2 | 5/3 | 2 | 3 | 4 | ||||||||
| 音符 | C | E | G | A | C' | C" | |||||||||
注意到我们在 C 和 C' 之间加入的第一个音符 G 的频率为 C 的 3/2 倍。因此,如果我们以 G 为起点,那么我们还应该加入一个频率为 (3/2)*(3/2)=9/4Hz 的音符。但是这个音符在第一个八音外面,我们还必须将它平分一次,使得新的音符进入第一个八音区,这就是频率为 9/8Hz 的 D。由此得到下表:
| 频率 | 1 | 9/8 | 5/4 | 3/2 | 5/3 | 2 | 3 | 4 | |||||||
| 音符 | C | D | E | G | A | C' | C" |
如果我们满足于现在的音节,那么我们得到的正是中国古代音乐的五声音阶。中国古代五声音阶:宫、商、角、徵、羽,相当于现代音乐的 C、D、E、G、A 五个音阶。不过,我们还希望加入一个 4/3Hz 的音符,即音符 F。用上面同样的方法,我们取 (5/4)*(3/2)=15/8 Hz 得音符,即得到音符 B。再将这两个音符填入表中,我们得到:
| 频率 | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 | 3 | 4 | |||||
| 音符 | C | D | E | F | G | A | B | C' | C" |
现在,如果音乐家们都以 C 作基调的话,上面的音符就可以奏出优美的旋律了。问题是他们在演奏中常常还会变换其它音符作基调。那么上面的这些音符是否还会保持和谐呢?答案是否定的。我们注意到,C 到 G 频率增加了 3/2 倍,这个关系显然应该保持。但是,当我们看表中的下一个音符从 D 到 A 频率增加却不是这个关系,因为按照这个关系,A 的频率应该是(9/8)*(3/2)=27/16 Hz。尽管 $27/16$ 与 $5/3$ 很接近,但它们并不严格具有和谐的关系。为了要达到全部的和谐,我们可以无限地加入新的音符,这显然是不可能的。那就是说,我们所需要的这个 $3/2$ 关系必须在某一个八音上停止。从数学的角度来说,我们现在面临的问题就是我们必须选择正整数 $m$ 和 $n$ 使得
$$( 3 / 2 ) ^ { m } = 2 ^ { n } , \quad m > 0 , \quad n > 0$$容易证明,这个方程没有正整数解。最接近的使得这个方程近似成立的正整数为 $m=12$ 和 $n=7$,因为这时我们有:
$$( 3 / 2 ) ^ { 12 } \cong 129.74633 \dots\text{ 和 } 2^7=128$$这说明,我们在 C 和 C' 之间需要 12 个能满足 3/2 关系的音符;而且它们中相邻的两个的频率比值是常数。现在我们来确定这 12 个音符。假定这个常数记作 R。因为我们需要 12 个音符,而且每高一个八度频率加倍,所以有:
$$R^12=2.$$这个方程的基本解为 $\sqrt[12]{2}=1.0594\cdots$。这是一个无限不循环小数 (无理数)。用等比序列 ${R^i,~ i=0,1,2,\cdots,11}$ 我们得到一个已经成为西方音乐律制核心的“十二平均律(equal temperament)”:
| 频率 (分数) | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 | ||||
| 频率 (小数) | 1.000 | 1.125 | 1.250 | 1.333 | 1.500 | 1.667 | 1.875 | 2.000 | ||||
| 音符 | C | C# | D | D# | E | F | F# | G | G# | A | B | C' |
| 十二平均律 | 1.000 | 1.059 | 1.122 | 1.189 | 1.260 | 1.335 | 1.414 | 1.498 | 1.587 | 1.682 | 1.888 | 2.000 |
比较表中的第二行和第四行我们发现,十二平均律所确定的音符与我们前面推导得到的 (毕达格拉斯的) 自然律制非常接近,而且在 C 和 C' 上它们重合。虽然它是人为地将一个音极按等比序列分成十二个相等半音,但是它解决了自然律制在转调上不和谐的缺陷,非常适合调式变换、和声写作和器乐演奏,极大地扩展了作曲和演奏的范围。相关的文献有[1,14]。
下面我们来说明这样的分法是最佳的。回忆十二平均律的确定是从方程
$( 3 / 2 ) ^ { m } - 2 ^ { n } = 0 , \quad m > 0 , \quad n > 0$ 的近似解得到的。把等式左边的差用 $Res(m,n)$ 表示,即 $Res(m,n) =(3/2)^m-2^n$。我们的近似解 $(m,n)=(12,7)$ 使得 $Res=1.74633\cdots$。
数学上把 $Res$ 称作剩余值。我们自然可以考虑这样的问题:如果我们再增加几个音符,效果是否会更好?用数学表达式我们可以把问题叙述成一个极值问题:
$$\min \{ \operatorname { Re } s ( m , n ) : m > 0 , n > 0 , \quad m~和~n~是正整数\}$$这个表达式是说要在所有的正整数组 $(m,n)$ 中寻求一组使得 $Res(m,n)$ 达到极小值。十二平均律表明
$$\operatorname { Res } ( 12,7 ) = \min \{ \operatorname { Res } ( m , n ) : 13 > m > 0,8 > n > 4 , \quad \text{$m$ 和 $n$ 是正整数}\}.$$这里我们限制了 $n > 4$,因为我们已有了五个音符。现在让我们来扩大搜寻范围。我们把问题简化成
$$\min \{ \operatorname { Res } ( m , n ) : 500 > m > 0 , \quad 500 > n > 4 , \quad \text{$m$ 和 $n$ 是正整数}\}.$$注意这里我们允许 $n$ 取值 $500$,尽管由於受到乐器和人体活动的范围,我们不可能让 $n$ 如此之大。会任意一个计算机语言的读者可以编写一个简单的程序去验证,这个极值仍然是在 $m=12$ 和 $n=7$ 时达到最小。有人曾经提出十九平均法。上面的简单讨论就说明这是不可取的。
上面的讨论假设了 C 的频率为 1Hz,当然这不符合实际。通常 C 调的频率为 262Hz,C 上面的 A 为 440Hz。以 A 调为基准加以类推,我们就得到了全部 12 个音节。重要的是,当一个音符升高八度后,它的频率加倍。例如 C' 调,其振动频率为每秒 528 次。
注意三角函数在这里的重要意义。事实上,利用三角函数我们也可以解释调音原理。具体的推导从略。近代数学中,由三角函数发展起来的一个分支叫作 Fourier 分析 (调和分析)。它在通讯和音乐方面有许多应用。比如,现代录音技术中消除噪音和人声等。数码音乐的创作只是将正弦波音 (Sine Tone) 处理后得出的声音。最近发展起来的小波分析也已经被应用于对音乐的研究。1
4. 对数螺旋线和十二平均律


值得一提的是,在中国最早 (1581) 利用数学制订出十二平均律 (或称十二等程律) 的是我国明朝音乐家朱载育。甚至早在南宋时, 乐律学家何乘天就创制新律, 成为最早用数学解决十二平均律的人。虽然所得的十二律还不是按频率比计算的真正平均律, 但实际效果已相当接近。在西方,十二平均律是由荷兰人斯特芬于 1600 年前后得到的。巴赫在推广平均律方面的贡献是众所周知的。他创作的《平均律钢琴曲集》为平均律建立了规则和典范。这是第一部实现平均律的作品,使人能在各调上作均等的弹奏。
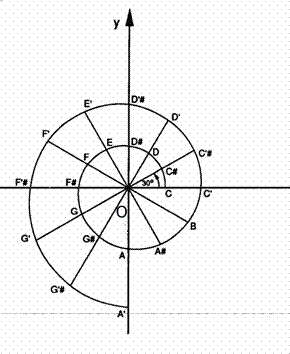
然而当巴赫试图推广十二平均律的时候却遇到了很大的阻力。幸运的是,巴赫本人热爱数学,他的音乐也具备高度的数学性。当他无法说服他的音乐家同事相信十二平均律的好处时,他向数学家约翰伯努利寻求帮助。伯努利随手画了一个对数螺旋线并在上面标了十二个半音。他对巴赫说,” 在这个曲线上,旋转同样的角度可以使它与原点的距离以同等比例增加。这不正是你现在所要的情形吗?” 他继续说,” 从一个音节到下一个音节,你只要旋转这个螺旋线使得你的第一个半音落在 $x$ 轴上;其它的音就会自动地落在其应到位置上。这简直就是一个音乐计算器!” (见 [2])。那么伯努利画的是个什么样的图形呢?让我们用极坐标来表示,中心在原点的对数螺旋线的标准方程就是 $r = e ^ { a \theta }$。按照伯努利的描述,曲线的起点为在正 $x$ 轴上的 $C(1.0, 0.0)$,然后依反时针旋转一周,每隔 $30 ^ { \circ }$ 或 $\pi / 6$ 就标一个点 (当然在这个方程中我们必须使用弧度)。这样一共有十二个点:C,C#,D,D#,E,F,F#,G,G#,A,A#,B。当曲线回到正 x 轴时,我们得到下一个 C,记作 C'。假设 OC' 是 OC 的两倍。那么 C' 的坐标为 $(2.0, 0.0)$。於是我们有,
$$2 = \mathrm { e } ^ { a 2 n }$$从而,
$$a = ( \ln 2 ) / 2 \pi _ { \circ }.$$于是利用指数函数和对数函数的性质,我们得到 $r$ 的极坐标方程:
$$r = \mathrm { e } ^ { ( \ln 2 ) \theta / 2 \pi } = \mathrm { e } ^ { \ln 2 ( \theta / 2 \pi ) } = 2 ^ { ( \theta / 2 \pi ) }$$注意到曲线上取的 12 个点的角度分别为
$$\theta _ { i } = n ^ { * } i / 6 \quad ( i = 0,1,2 , \ldots , 11 )$$我们又一次得到了前面的十二平均率的 12 个点:
$$r _ { i } = 2 ^ { ( \theta / 2 \pi ) } = 2 ^ { \left( n ^ { * } / \left( 12 ^ { * } n \right) \right) } = 2 ^ { i / 12 } \quad ( i = 0,1,2 , \ldots , 11 )$$对数螺线又称等角螺线。伯努利的哥哥雅各布伯努利从 1691 年就开始了陶醉于对数螺线的研究。他发现对数螺线经过各种变换后仍然是对数螺线。这与十二平均律允许灵活转调是一致的。
5. 黄金分割和斐波那契序列

数学在音乐的应用方面还有一个显著的领域是黄金分割法。原中国科学院数学研究所所长华罗庚从 1964 年起推广优选法。他在单因素优选问题中,用得最多的是 0.618 法,即黄金分割法。黄金分割线的神奇和魔力,在数学界上还没有明确定论,但它屡屡在实际中发挥我们意想不到的作用,事实上,凡是可以度量的属性都有理由运用黄金分割。音乐也不例外,而且很多。

在制作小提琴时,提琴的结构中的黄金分割律是使小提琴音色优美动听的一个重要因素。有人以 “355 型” 小提琴(即 4/4 小提琴)为例,找出了其结构中的 14 个黄金分割关系。在作曲中,传统的 ABA 三部曲式结构,体现了对称均衡的形式美法则。很多作品把乐曲的高潮位置定在黄金分割点左右。美国底特律的一家录音机构 (The Recording Institute Of Detroit) 根据黄金分割的比例建造了他们的录音棚。据说其效果显著地好。在中国,有人研究发现,二胡的千金放在 0.618 的位置上发出的音最为优美。还有人严格计算了《义勇军进行曲》中的分段,发现它的转折点也是在黄金分割点附近。在音乐作品中,被后人讨论最多的是莫扎特。他的《D 大调奏鸣曲》中明显使用黄金分割。第一乐章全长 160 小节,再现部位於第 99 小节,不偏不依恰恰落在黄金分割点上(160*0.618=98.88)。他的《C 大调第一协奏曲》、《第三 G 大调》、《第四 D 大调》、《第五 A 大调》小提琴协奏曲和一些其它钢琴协奏曲中也同样使用黄金分割的痕迹。尽管人们无法判断是否莫扎特有意地使用了黄金分割来改善他的作品,但他热爱数学是众所周知的。他甚至在他的许多乐稿的边缘写下数学公式。读者若对莫扎特作品的深入研究有兴趣的话,可以参见 [3]。除了莫扎特的奏鸣曲外,贝多芬、巴赫、巴尔托克、德彪西、舒伯特、埃里克 - 阿尔弗雷德 - 莱斯利 - 萨蒂、奈格 、亨德尔、维瓦尔弟的音乐里也蕴藏著黄金分割的完美和谐。虽然他们有些人不一定知道黄金分割,但是既然毕达哥拉斯可以凭某种第六感官断定 0.618 是个神奇的比值,那么为什么伟大的艺术家们不可以有类似的直觉呢?
与黄金分割紧密相关的是斐波那契 (Leonardo Pisano Fibonacci,1175?-1250) 序列。这个序列从零和一开始,后面的每一个数是其前面两个数的和。它的前十四项就是
0 1 1 2 3 5 8 13 21 34 55 89 144 233
如果把它的单项记作 $a_n$。那么有,$a_1 = 0,a_2 = 1$,以及 $a_n=a_{n-1}+a_{n-2}~(n>2)$。奇妙的是,这个序列与黄金分割也是相关联的:任何两个相邻项的比值 $a_{n-1}/a_n 近似于 $0.618$,而且越往后其比值越接近 $0.618$:
$$a _ { 1 } / a _ { 2 } = 0.00000 , a _ { 2 } / a _ { 3 } = 1.00000 , a _ { 3 } / a _ { 4 } = 0.50000 , a _ { 4 } / a _ { 5 } = 0.66667 , a _ { 5 } / a _ { 6 } = 0.60000\\ a _ { 6 } / a _ { 7 }=0.62500 , \quad a _ { 7 } / a _ { 8 } = 0.61535 , \quad a _ { 8 } / a _ { 9 } = 0.61905 , \quad a _ { 9 } / a _ { 10 } = 0.61765 , a _ { 10 } / a _ { 11 } = 0.61818 $$反过来的比值 $a_n/a_{n-1}$ 则近似于 $0.618$ 的倒数 $1.618$。用数学中的极限的概念,就是说
$$\lim _ { n \rightarrow \infty } \left\{ a _ { n - 1 } / a _ { n } \right\} = k , \quad \lim _ { n \rightarrow \infty } \left\{ a _ { n } / a _ { n - 1 } \right\} = \varphi.$$这个序列是十三世纪意大利数学家斐波那契为解决兔子繁殖的研究过程中最先使用的。后人发现它在自然界有多方面的应用。其应用之多以致人民专门发行了斐波那契季刊 (Fibonacci Quarterly)。在英国还有一个“斐波纳契数列”交响乐团 (The Fibonacci Sequence)。
黄金分割主要应用于连续变量的属性,而斐波那契序列则在离散的变量里常常现身。我们可以把斐波那契序列看作黄金分割离散化以后对黄金分割的一种近似。让我们先来看看钢琴的健吧。钢琴八度音之间有 5 个黑键和 8 个白键共 13 个半音阶,这正是斐波那契序列中的第 6 至 8 项。
再来看看作曲家们是如何把这个神秘的数例与他们的乐曲巧妙结合的。法国作曲家萨蒂喜欢斐波那契数,在他众多的曲子中正好也显现出了这一用黄金分割为结构的乐曲。例如,《来自玫瑰与十字架的第一钟声》(Sonneries de la Rose+Croix,又称《玫瑰十字教之钟》) 这部作品。除了无节拍号、小节线和终止符外,作者就明显地运用了 &“黄金分割”,将段落配置得十分巧妙。这组钢琴曲共包括三首。它的第一首为《玫瑰十字教之歌》 (Air de l'ordre,又称《序列之歌》),全曲的拍数为 233 拍,呈示部的拍数为 144 拍,正好落在斐波那契序列的第 14 和 13 项上。笔者猜测萨蒂之所以如此精心地策划这部作品可能是因为受玫瑰十字教的影响。玫瑰十字教是个神秘宗教组织,它主张把古老的神秘智慧传承下去。而斐波那契数列正好与古希腊的神秘数 0.618 密切联系。
另一位明显应用了斐波那契数列的作曲家是巴尔托克。他在作曲中迷恋大自然中的形式美,这正好与斐波那契数列在自然界的天衣无缝般的应用相吻合。在生活中他也是不断地扩大他的植物、昆虫和矿物的收藏。向日葵是他最喜欢的植物,而向日葵的葵瓜子排列正是斐波那契螺旋。他把这一现象应用在作曲中,而且比萨蒂应用的更加淋漓至尽。比如,他的《舞蹈组曲》 (Dance Suite) 就是按照斐波那契序列创作的:第一乐章是大二度 (2),第二乐章是小三度 (3),第三乐章则是前两首的和 (2 + 3 + 2 + 3 + 2),最后第四乐章是第二、三乐章的和 (8 = 3 + 5)。再比如,他的《为弦乐,打系乐器及钢琴所写的音乐》(Music for Strings, Percussion and Celesta)里有 89 小节 (斐波那契数列的第 12 项),中间又分为 55 和 34 小节的两部分,55 小节的部分又分为 34 和 21 小节的两段,作品在第 55 小节上达到高超。这里从局部上所有的数字都落在斐波那契序列上,从整体上又符合黄金分割,真是妙不可言。从这些例子我们看到,斐波那契数列不仅可以在整体分段上运用,也可以在节奏、音高以及配器法式上实现。
斐波那契序列还有一个不太知名的变型是由法国数学家卢卡斯定义的。他的序列称作卢卡斯序列。这个序列的定义是:
2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, ...
从第三项以后,每一项也是由前两项的和生成的。而且,它也有类似斐波那契序列的极限 (趋於黄金分割) 的性质:
4/7 = 0.7514, 11/18 = 0.6111 and 76/123 = 0.6179, 123/199 = 0.6181, 199/322 = 0.6180, ...
萨蒂的作品《烦恼 (Vexations)》就体现了这个序列。比较卢卡斯序列和斐波那契序列,我们发现它们的区别仅在於第一和第二项,后面一般项的规则是相同的。由这两个序列得到的比值序列 (即每项与前一项的比) 都以黄金分割数为极限。这一现象不是偶然的。事实上,广义斐波那契数列都具有这个特性。
在今天,不仅许多人在研究曲谱时有意地寻找其中的数学形式,一些象曼格温 (Casey Mongoven) 那样的现代作曲家有意识地在他的作品中使用黄金分割和斐波那契序列。电子音乐先锋克塞纳基斯 (Iannis Xenakis,1922-2001) 甚至在他的主要作品中应用了更现代的数学理论 (随机分布、集合论、博弈论和随机漫步等),创作于 1956 年的 “概率的作用” 是其代表作之一。同类型的作品还包括:根据德国数学家高斯的理论创作的 “ST/10” 和“Atrees”、根据马尔可夫链创作的 “Analogiques”、根据运动原理创作的“Duel”和“Strategie”以及其第一部电声作品 “Bohor” 等。他因此被印第安那大学聘请为数学音乐和自动化音乐教授。人们越来越意识到许多自然的声音有着潜在的数学逻辑,随着时间的变迁,人类可能已经变得对某些声调和形式有特殊的敏感。也许诸如斐波那契和黄金分割这样的关系可能会帮助另一个文化了解我们人类是生活在一个什么样的声音环境中。
5. 结束语
在以上的讨论中,我们不但用到了无理数、三角函数和它们的和差性质、解析几何中的极坐标、三角级数、等比序列、斐波那契序列、代数方程、指数和对数的性质、黄金分割,还简要地涉及了偏微分方程和 Fourier 分析等现代数学。纵观数学走进音乐的历史,可以说毕达哥拉斯发现了它的地位,莫扎特、巴赫证明了它的地位。尽管音乐的普及不需要数学的引导,但是音乐理论的研究却大大地需要数学的帮助。如果读者在阅读本文之前还怀疑数学在音乐中的地位的话,那么现在是否应该有一个全新的认识呢?
参考文献:
杨健,“走进琴弦的世界 -- 谈近三千年来人类对琴弦的研究及引发的思考中” 的附录 “拨弦模型的建立、求解和分析”,《自然杂志》2004,26(3):177-183
EliMaor,巴赫与伯努利的历史性会见 (A Historic Meeting between J.S.Bach and Johann Bernoulli),E: The Story of a Number,Princeton University Press, 2009
翁瑞霖,数学与音乐的对话: 探讨莫扎特音乐德数学应用及其效应,国立台湾师范大学学报, 49(2), 85-100
吴林,文化的贯通 - 音乐与数学的融合
侯德明,萨悌钢琴曲《运动与娱乐》特殊创作理念之探讨,国立中山大学音乐系研究生论文
黄力民,音乐中的数学,三思科学电子杂志
蔡松琦、蔡幸子,音乐与数学,钢琴宝典,华南理工大学出版社 2001 年 7 月第 1 版
Music and Mathematics
Paul Cox, Math and Music: A Primer
Robert Orledge, Understanding Satie's'Vexations'
Terry Ewell, Use of the Fibonacci Series in the Bassoon Solo in Bartok's Dance Suite, The Journal of the International Double Reed Society 17 (July 1989): 4-6.
Phil Tulga, Sequencing with Fibonacci
Music and the Fibonacci Series
John Allen, On Rabbits, Mathematics and Musical Scales
联接:
| 作者: | 蒋迅 |
| 原文链接: |
本文发表在 《数学与人文》丛书 第一卷。 |




