组合爆发和旅行货郎问题
Peter Gritzmann, René Brandenberg
选自《最短路径的秘密 —— 一次数学上的探险》(Springer,第 3 版,2005 年),第 42–48 页,第 286–294 页,以及第 346–355 页。
一场不危险的爆炸
晚上,Ruth 和他的父母一起坐在电视前。他们没有说一旬关于她的计算机的话。Ruth 并不想谈及这个话题,而且她的父母看上去也完全缺乏兴趣。正常情况下,他们总是想要清楚地知道所有细节。在上个秋游之后,爸爸妈妈已经开始对她感到非常困扰,而且现在他们不知道该怎么处理计算机的问题。不论如何,这是一件好事,因为 Ruth 自己也不知道该怎么做。至今,除了读了几封电子邮件,她并没有比 Vim 知道得更多。对于 Ruth 来说,父母的缺乏兴趣看上去是很奇怪的。也许对于 Jan 来说要简单一些。他们似乎想知道关于他的一切。而 Ruth 告诉她父母所有事情,嗯,所有你想要告诉父母的事情。
接下来 Ruth 去了厕所。已经很晚了。明天早上闹钟会无情地将她从美梦中惊醒。
但是想要再看一眼 Vim 的诱惑是这么大。经过一刻钟之后,她忍不住开口自言自语。
“嗯,你,现在不是去睡觉的时间吗?”
“什么意思,你听上去就像我的爸妈。”
“不会再这样了。我只是担心你的爸妈如果发现在这个时间点你还在电视前的
话会收走我的这个权利。”
“不用担心,他们不会知道的。”
“现在你真的想要在睡前再看看数学吗?”
“路程规划! 你想要给我解释怎么找到最短路径。”
“这个我们今天没有时间解释了,但是我们也许还可以解释这个方法的基本思路是怎么来的。”
“这是显然的! 我们需要计算最短路径。这有什么好解释的?!”
“你马上就会知道了。但是我想要先说一点。我会试若用简单的小例子来给你解释。在这些例子中,大部分时候你可以测试所有的可能的路径并且找到其中最短的那条。但是在实际问题中,我们可能会面对成百上千,甚至是几万个节点,在这种情况下,因为可能的路径的数植太多了,导致即使是世界上最快的计算机也没有办法
测试所有的可能性。”
“为什么呢? 一台计算机可以在一秒钟进行几千次的运算呀。”
“好吧,假设有下面这幅图,我们想要找到其中最短的路径。”
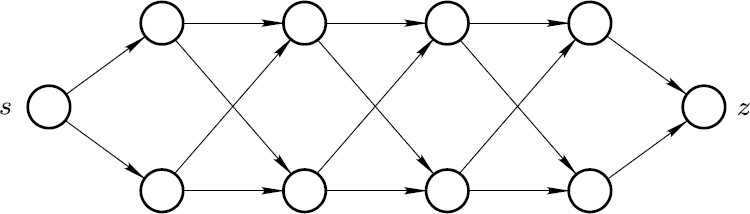
“这幅图并不是很大啊。”
“它也不是很复杂,而且当我们知道每条路确切的长度的时候,要找到最短的路径并不是很难。但是用这幅图已经足够来理解路径数植的问题出在哪里了。设想我们想要从起点(就是图上标记为 s 的点) 走到终点(就是图上标记为 z 的点)。有多少不同的 s-z 路径,也就是从 s 到 z 的路径呢?”
“啊,有一些呢。如果我想要数出所有不同的路径,肯定会犯一些小错误的。”
“不用担心,这个问题实际上并不是那么困难。我特意选择这幅图是有原因的。事实上你只需要很系统地跟随我的指示,这样就可以轻松数出不同的路径的数植。将所有节点分为一层一层来考虑有助于你解答问题。首先,从 s 出发有多少种可能性呢?”
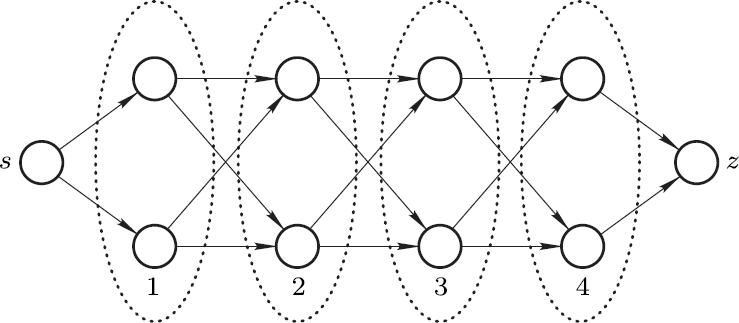
“2 种。”
“然后你有多少种可能性,从层数为 1 的点,也就是你现在所在的点继续前进
“嗯,现在我了解你是什么意思了。从起点 s 出发有 2 种可能性,要么向上走,要么向下走; 同样,不论走到哪个节点,我们依然有 2 种不同的选择继续向前进,同样的方向或者走去另外一个方向。”
“ 直到我们到达终点 z 之前的节点为止。从那里,我们只有一个选择,就是
走向 z。所以现在我们一共有多少种可能路径呢?”
“从起点 s 出发到第一层的点有 2 种方法,接下来我们又有 2 种方法; 也就是说,有 4 种不同的方法到达第二层的点 ”
“ 接下来每个点上又有 2 种不同方法前进,也就是说有 8 种方法可以走到第三层的点,16 种方法走到第四层的点,接下来我们就达到了终点 z。所以我们一共 16 条不同的路径。”
“你不是想告诉我,计算机对于数这样的路径的数植有困难吧!”
“当然不是。但是我们再假设,将上面的这个图增加两个节点。那么现在存在多少条路径呢?”
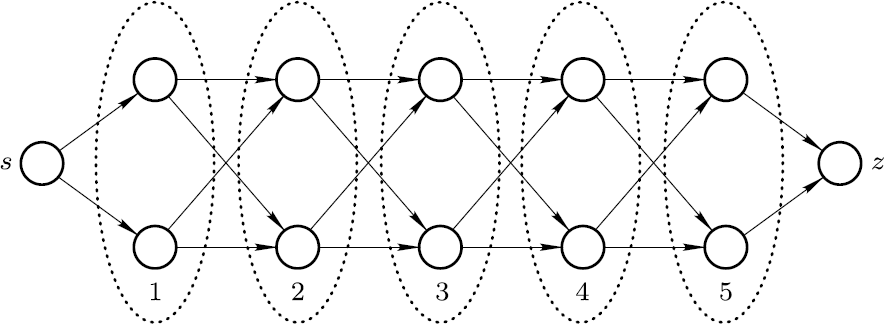
“当然就是原来的路径的两倍: 32。”
“很好。你知道用幕次 25 吗?”
“当然,25 = 2 · 2 · 2 · 2 · 2 = 32。”
“那么如果你只想要知道起点和终点之间的层数,那是多少呢?”
“5。所以意思是说路径的数植是 2 的层数的幕次?”
“对,而且节点的数植是 2 (这是指起点 s 和终点 z) 加上 2 倍的层数。”
“对了,在第一种情况是 2+ 2 · 4 = 10,第二种情况是 2+2 · 5 = 12,但是路径的数植分别是 24 = 16 和 25 = 32。现在我知道为什么你想要写成 2 的幕次了。”
“你可以发现,对于任何整数 n,有 n 层意味若存在 2n 条不同的路径,但是却只有 2+2 · n 个节点。”
“所以呢?”
“如果我们的图现在有 50 层,也就是说总共有 102 个节点,你当然不想把这幅巨大的图给画出来然后逐个数吧?”
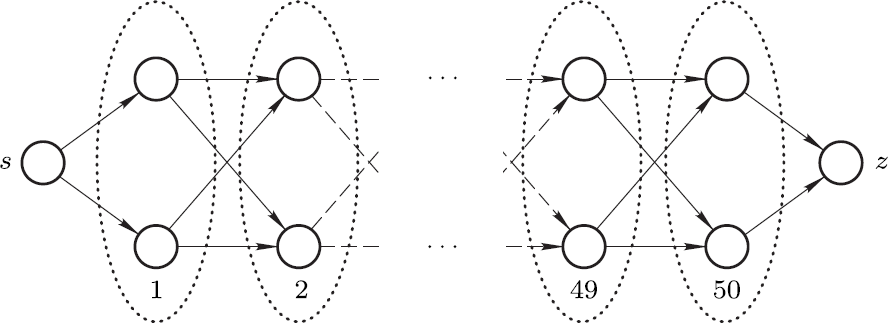
“如果是你曾经说可能会有上千个点的图,当然不想。”
“但是在这种情况下根据我们的公式:
250 = 1125899906842624,
也就是说这已经有一千多万亿条路线了!”
“天啊! 这也太惊人了! 但是对于我的新计算机来说应该是没问题的,对吧?”
“现在让我们从另一个角度来看。假设你的计算机可以在一秒钟计算一百万条路线,那么它就需要至少十亿秒。六十秒是一分钟,六十分钟是一小时,二十四小时是一天。也就是说,每天有 60 · 60 · 24 = 86400 秒,所以一年有 86400 · 365 = 31536000
秒。这样的话你的计算机大约需要
$$\frac { 1125899906842624 } { 31536000 }\,年$$也就是说差不多 36 年才能检查完所有的路径。”
“这也太久了吧!”
“如果我们的图里再增加几层,所需的时间会更加惊人。在这里我给你列了一个表格,其中你可以看到对于不同的层数,相应的节点数,路径数以及所需要的时间长度。”
层数 |
节点数 |
$s-z$ 路径数 |
计算时间 |
5 |
12 |
32 |
0.000032 秒 |
10 |
22 |
1024 |
0.001024 秒 |
20 |
42 |
一百万 |
1 秒 |
30 |
62 |
十一亿 |
18 分钟 |
40 |
82 |
一兆 |
13 天 |
50 |
102 |
一千兆 |
36 年 |
60 |
122 |
一百京 |
3700 年 |
70 |
142 |
十万京 |
三千七百万年 |
80 |
162 |
一亿京 |
2.6 Au |
90 |
182 |
一千亿京 |
两千六百 Au |
100 |
202 |
一百兆京 |
两百七十万 Au |
260 |
522 |
1.9 Aau |
* |
“哇! 这么大的数字已经让我看晕了。在这个表格里的 ‘Au’,‘Aau’ 和星星是什么意思呢?”
“‘Au’ 是我自己创造的符号,它表示的是十五亿年。这差不多是我们的宇宙现在的年龄。一个'Aau'表示的是整个宇宙中所包含的原子的数植。假设我们的计算机中可以找到地球上的每一个原子,那么这台计算机大约需要六万五千 Au 才能检查完一幅 260 层的图中的所有路径。单独的一台计算机大约需要 6 · 1064 年来完成这个过程 —— 当然这个数字太大了,所以在表格中我就用星星符号来表示它。”
“啊,这样。超过 50 层的图需要的时间会长一些。但是如果我现在有一台好得多的计算机,例如说一秒钟可以检查一千兆路径,那么对于一幅 50 层的图我们只需要一秒钟就可以了。”
“对的。但是即使这样的一台超级计算机也需要 38 年来计算一幅 80 层的图,对于一幅 100 层的图则需要四千万年的时间。我甚至不想提及 260 层的图。”
“而且事实上这些图并不是那么大。”
“在数学中我们称这种情形为组合爆发,因为只需要增加少数的点就能造成路径数植激增。”
“真的! 所以事实上我们需要的是一个更好的方法来检查这些路径! ”
“对了,但是现在你真的需要去睡觉了。哦,我现在又变成 ‘家长’ 了!”
“没事,这是你的权利。但是你可以最后简短地告诉我,地球上或者宇宙中原子的数植大约是多少吗?”
“这个你可以上网看,网址是:
http://www.harri-deutsch.de/verlag/hades/clp/kap09/cd236b.htm.”
“好吧,那么,明天见!”
“好梦!”
Ruth 感到震惊。仅仅添加几个新的节点就能够导致可能的道路的数植的巨大变化。当然,我们需要找到一个聪明的方法来试遍所有的解答。但是这个方法到底是什么呢? Ruth 想若想若,慢慢进入了梦乡。
一个业务员的紧急情况
第二天早上,当 Ruth 从楼梯上下来的时候,她的妈妈已经醒了。她看上去有一些紧张。当 Ruth 询问的时候,她告诉了女儿昨天和 Ruth 的爸爸的通话内容,他说大约还需要额外的两天时间在外出差。一些额外的日程安排把他的行程搞乱了。于是现在 Ruth 的妈妈开始担心已经计划好的假期。如果真的要延长出差时间的话,那么她和 Ruth 将要在星期六单独出发前往法国。Ruth 的妈妈也不是那么喜欢自己开车,但是现在看起来她需要全程自己一个人坐在方向盘前。
假期! 最近几天 Ruth 完全忘记了这件事情,她和父母将要在普罗旺斯度假三个星期。在爸爸预订度假屋的时候,她当时非常兴奋,但现在似乎热情有些消退了。让事情变得更糟的是,妈妈坚持度假的时候爸爸不能带手机或计算机,因为他需要完全的放松。这个“信息拦截” 的规定也同样适用于 Ruth。
在第一个课间休息的时间,她告诉了 Jan 她们家的旅行计划。Jan 也不是很开心,因为这样他们会有几个星期不能见面而且也不能互相发邮件。但是他想要试试能不能说服家人去拜访他们的一个亲戚,这样在假期的后半段时间他们就可以一起度过了。
Martina 走向他们两个并且问他们是否有兴趣晚上一起玩一个她在生日时收到的新游戏。刚开始 Ruth 并没有兴趣加入,但是 Jan 觉得这是一个好主意,总好过两个人“愁眉相对”。
下课后开始了暑假排队的第一次组织会议。在最初的兴奋之后,Ruth 开始对此有些不确定。当然,如果要策划一些真的很有创新的活动,现在已经太晚了。无所谓了,只要和 Jan 在一起,准备工作一定会很有趣的。
在准备会议之后 Jan 必须先回家。他的妈妈请他帮忙采购一些东西。当他和 Ruth 会合的时候,距离和 Martina 的约定还有一些时间。
“你好 Vim。昨天你想要给我们解释一些关于 ‘知足’ 的问题。”
“哦,今天你们的时间有些紧张。我可以给你们介绍一个新问题吗?”
“当然,只要这个问题足够有趣!”
“假定一个保险业务员希望拜访一些客户。下面的图表示的是这些客户的住所,以及各自住所之间的距离。”
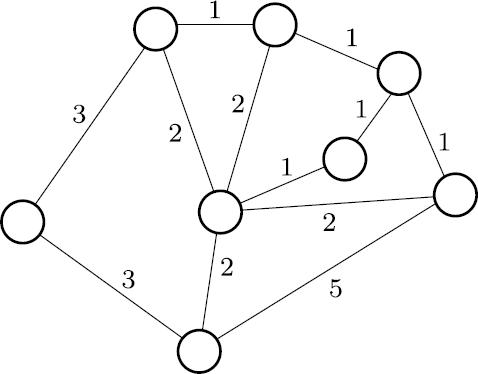
“为了节约时间和费用,这位业务员想要尽植好好安排他的日程,使得他只需要走最短的路就能拜访所有的客户。”
“对啊。我们想要将路线最短化。这一次我们想要寻找的最短路线是一条经过所有节点的路径,而不是通过所有的边—— 这是不同于中国邮递员问题之处。”
“看,Jan! 那个骑士巡逻问题只是一个预热而已。事实上 Vim 真的会给我们一个很实用的运筹问题!”
“也就是说,我们想要找到最短的哈密尔顿圉?”
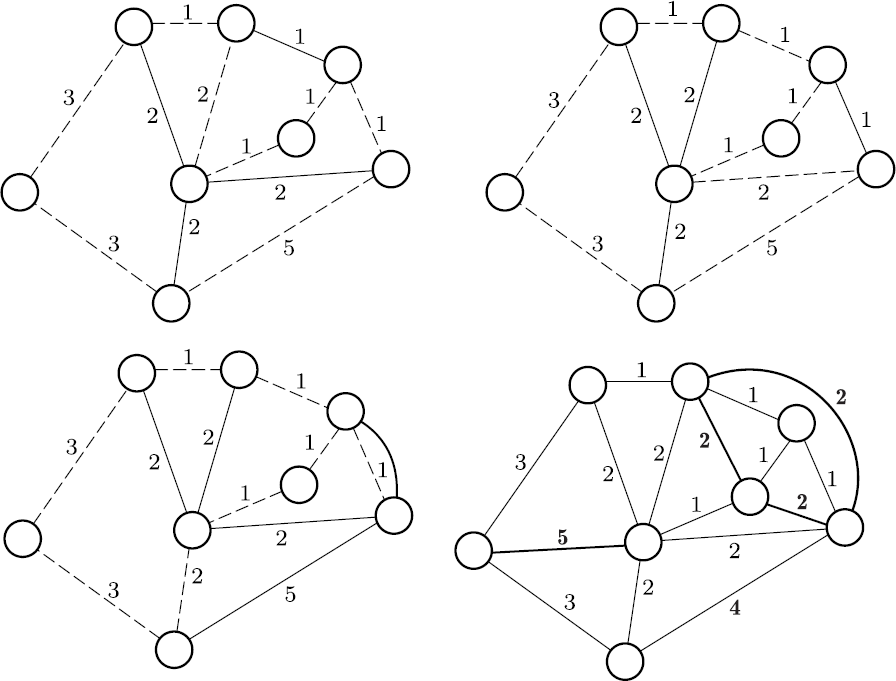
“部分正确。首先我们并不禁止这个业务员多次经过同一个村子,所以他不一定需要依照一个哈密尔顿圉旅行。看,这幅图里有两个哈密尔顿圉,而且两个圉的长度皆为 17。但是最下面那个图里展示的路线的长度只有 14,即使在这条路径中,我们重复走过了右边的边,所以经过右上角的节点两次。”
“啊哈! 但是这样的话,我们的解答就不是一个哈密尔顿圉了。为什么你回答说‘部分正确’呢?”
“我们可以将这个图拓展为完全图,正如我们在解决中国邮递员问题时所做的那样。接下来我们只要将额外添加的边的权重定为在原图中它的两个顶点之间的最短路线的长度即可。例如在这个例子中,我可以像下图一样添加四条 ‘新’ 的边 (粗线)。但是右下角的那条边的长度产生了变化。在最终得到的图中,在这两个点之间存在的是一条长度为 4 的边。”
“明白了。最短的距离是那位业务员在这些地点之间运动的距离。但是他不能随意行走,也不能自己创造道路。所以我们现在需要确定任意两个点之间的最短距离。我从来没有想过我们真的这么经常需要面对这样的问题。”
“在一个完全图中一定存在一个对于业务员而言最佳的哈密尔顿圉。在这里就是那条长度为 14 的路径。这条路线包含了我们额外添加的一条边。”
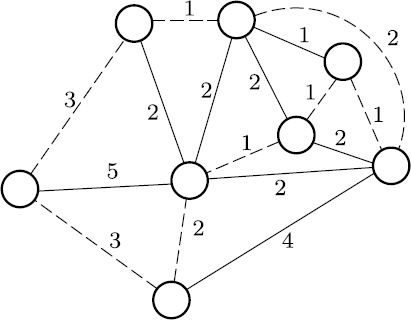
“明白了,我们这里所有的边的长度都是两点之间的最短距离,所以这个距离不可能比这个更小。”
“ 这个在一幅图中寻找最短哈密尔顿圉的问题被称作“旅行货郎问题” (英语中为 Travelling Salesman Problem),或被缩写为 TSP 问题。它可以被称作图论所有问题中最著名的问题。很多至今仍在使用的算法最早便源于对 TSP 问题的研究。将图中的节点对应于城市,那么这个问题就是要寻找一条经过所有城市的最短的旅途。”
“ 于是我们要为保险公司的业务员们寻找一条最好的路线 ”
“ 或者公司的出差线路也一样。在 http://www-m9.ma.tum.de/dm/java-applets/tsp-afrika-spiel/ 中你可以试若自己找一条经过 96 个非州城市的最短路线。当然我们从 一个城市飞到下一个,所以这里我们展示的是各个城市之间的飞行路线。”

“太好了! 我们现在就来试试!”
“你先来! 我现在去厨房烧壶开水。接下来再轮到我。我们来看看,究竞谁能找到比较短的路线。”
“那就让 Vim 做裁判,保证没有人作弊。”
说到做到。当 Ruth 在厨房烧水的时候,Jan 选择了自己环游非州的路线; 长度为 60352 km。经过漫长的等待,Ruth 的水终于沸腾了,她带回了开水和两个杯子。现在轮到她来选择路线了: 60009 km!
“看,Vim,我完胜了 Jan。”
“不要得意忘形了! 我只能说这是一个很接近的结果。而且你的路线肯定也不是最优的。”
“但是不可能短太多了,是吗,Vim?”
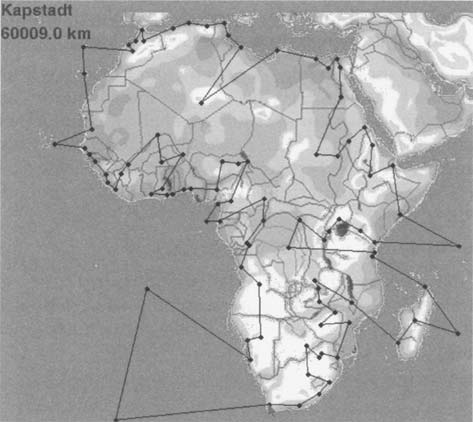
“最优的路线长度是 55209 km,也就是说短了将近 5 km。”
“哦,也就是说我们还可以再省下来一些时间和费用。看起来你作为一个旅程规划者的前景不是那么好哦,Ruth。”
“是说你吧,你的路线比我的还长呢。但是我觉得找到最短路线不是一件特别困难的事情。”
“好啊。谁先找到的话,另一个人给他/她买冰激凌吃。但是 Vim,你之前提到过,人们发展了很多针对 TSP 中困难的问题的理论和方法。但是真的有那么多像我们的例子一样复杂的差旅吗?”
“想要找一个需要经过所有城市的最短的出差路线的问题是对于 TSP 一个很好的演绎,这样我们可以比较容易介绍这个问题的背景设定。但是这个问题当然还有很多其他的重要的应用,例如我们的电视、计算机、洗衣机里的集成电路的制造。”
“这和规划路线又有什么关系呢?”
“我们需要在一块长方形的金属板上面用机器在设计好的位置打上洞,使得之后可以在这些位置放上电子元件。这些洞看上去差不多是这样的:”
“这类工作现在几乎都是由机器人来完成。不管怎么说都是很快可以完成的。”
“但是机器人必须先知道它应该以什么顺序来打洞。下面是两种不同的顺序的可能性。图中黑色的线表示的是打洞器移动的路线。你们有没有发现这两幅图的不同呢?”
“当然了! 第一幅图中机器移动的距离比较长,显然这幅图比第二幅看上去要复杂得多。”
“不论如何,第一幅图中的那个大写的“N” 并不是一个好兆头。路线的长度和机器人的速度有关系吗?”
 (图片来源: M. Gro¨tschel,M. Padberg-Die optimierte Odyssee,Spektrum der Wissenschaft,Digest 2/1999,3.32-41)
(图片来源: M. Gro¨tschel,M. Padberg-Die optimierte Odyssee,Spektrum der Wissenschaft,Digest 2/1999,3.32-41)
“在第二幅图中黑线的长度几乎是第一幅图中的一半。让我们简单地计算一下。假设打洞器需要打很多洞,它用第一种方法打一块板需要 5 个单位时间。其中机器人需要 3 个单位时间来打洞,另外 2 个单位时间是洞与洞之间的移动所花费的。”
“那么使用第二种方法它只需要 4 个单位时间 —— 3 个单位时间用来打洞,只需要 1 个单位时间用来移动。”
“正确。这样每天机器人可以比原来多打 20% 的集成电路板。”
“也对,这个和机器人的快慢是没有关系的。”
“而确定一个最佳的顺序无非就是我们的旅行推销员问题的解答 ”
“ 如果我们把打洞器看成是推销员的话。通过你的解释,我觉得我知道这幅图是什么样子的了。这些洞就是节点,任意两个节点之间都存在边,因为打洞器可以在任意两个洞之间移动。边的长度就是打洞器从一个顶点移到另一个所需要的时间。”
差旅的成功
“告诉我们,是谁最早的想法,用 ‘奶酪切片’ 来解决旅行推销员问题。一定是个瑞士人,对吗?”
“在 20 世纪 40 年代末,旅行推销员问题是一个非常流行的问题。当然,这些 ‘好听的名字’ 也对此有一些贡献。但是真正起决定性作用的应该是它和一些实际问题的紧密联系,例如物流问题或者交通问题,这些问题在当时已经得到了很多成果,而不像 TSP,显然是一个很困难的问题。”
 (图片来源: M. Gro¨tschel,M. Padberg-Die optimierte Odyssee,a.a.o.)
(图片来源: M. Gro¨tschel,M. Padberg-Die optimierte Odyssee,a.a.o.)
“果然如此!”
“对于 TSP 问题研究开始于一个数学中的新领域的诞生: 组合运筹学。在 1954年,George Dantzig,Ray Fulkerson 和 Selmer Johnson 解决了有 49 个城市的环游问题。在 http://www.math.princeton.edu/tsp/history.html 中我们可以找到下面这幅图。”
“环游美国之旅? ”
“对,确切地说,是经过当时美国 48 个州的 48 个大城市,以及华盛顿。说说看, 为此他们发展了什么方法?”
“不知道。我觉得应该是你之前跟我们解释过的某种方法吧。”
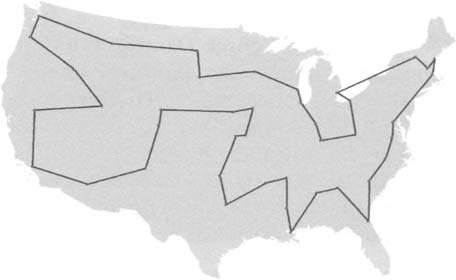
“对。在这里他们就是使用了 ‘奶酪切片’ 来得到分支限定法的下界。Dantzig 还在 1947 年找到了一种最快的方法来确定所谓的奶酪多面体的最优角。 在他的主页 http://www.stanford.edu/dept/eesor/people/faculty/dantzig/ 中我们可以找到他的一张照片。”
 Dantzig
Dantzig
“所以说他也是一个奶酪爱好者?”
“不知道。不论如何他的个性应该是很有意思的。你们想要听一个关于他的轶事吗?”
“当然! ”
“在 George Dantzig 上学时他曾经上过一门课,在这门课上,教授的习惯是在刚开始上课的时候在黑板上先写上下次上课前需要解决的作业题。有一次他上课迟到了,但是幸运的是老师写的那几个题目还留在黑板上。回家之后他就开始准备做作业。但是他发现这次的作业比原来的要困难一些,但是最后他还是成功地解决了问题。”
“恩,那么这个故事的意思是什么?”
“事实上,这次教授在黑板上写的并不是作业题,而是写了两个在当时让很多数学家咬牙切齿的未解决的问题。”
“哈哈。也许如果他事先就知道这些问题是未解决的难题的话,他根本就不会试若解决它们!”
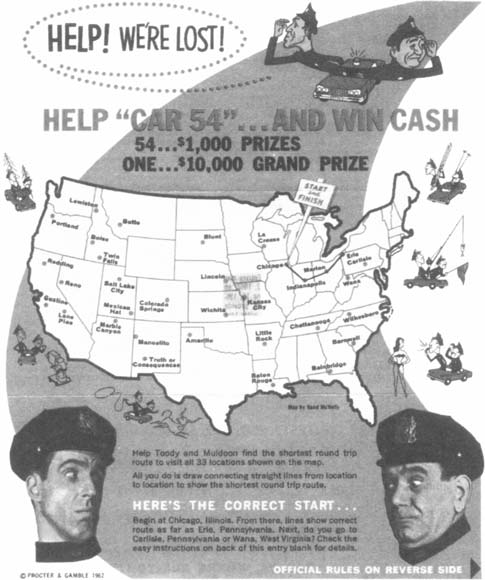
“也许吧。幸好他当时并不知道而且马上得到了博士学位。回到 TSP 问题: 直
到 1962 年的时候,旅行推销员问题一直是非常流行的,美国一个很大的公司,名为'Procter and Gamble',举办了一个 TSP 竞赛。当时的海报是这样的。”
“一等奖的奖金是一万美元 —— 很不赖啊! 要是我也能参加就好了,我们三个一定可以找到最佳路线的!”
“49 个城市真的不是很多。你的打洞机的游戏比这个问题的节点要多得多。”
“对。肯定需要一些时间才能真的解决现实生活中的大问题。在 1977 年,Martin Gro¨ tschel 创造了 120 个节点的新的世界纪录,并且在 1987 年,他和 Olaf Holland 一起确定了一个最佳的拥有 666 个节点的 ‘环游世界之旅’。在 1990 年还将这个问题印在了T 恤上。”

“啊哈,80 天环游世界!”
“应该说是 666 站环游世界。我们的非州谜题就是这个环游世界问题的其中一部分。”
“现在的计算机比那时候的可是快了超级多啊!”
“即使是现在最好的计算机也没办法简单地尝试所有的可能性来解决 Dantzig,Fulkerson 和 Johnson 解决的那个 49 个城市的问题。事实上在这段时间内,正如计算机技术一样,数学也同样有了巨大的进步。仅仅在四年之后,David Applegate,Robert Bixby,Vasek Chva´tal 和 William Cook 找到了一个有 3038 个节点的最佳环游世界之旅。”
“于是这个时候我们已经可以解决所有的只有一两千个节点的环游问题。”
“小心。在 1991 年的关于 3038 个节点的纪录只是意味若一个特定的问题被解决了。例如还有一个只有 225 个城市的问题,直到 1995 年才被击破。在 http://www.cs.rutgers/edu/∼chvatal/ts225.html 中你们可以看到这个问题。”
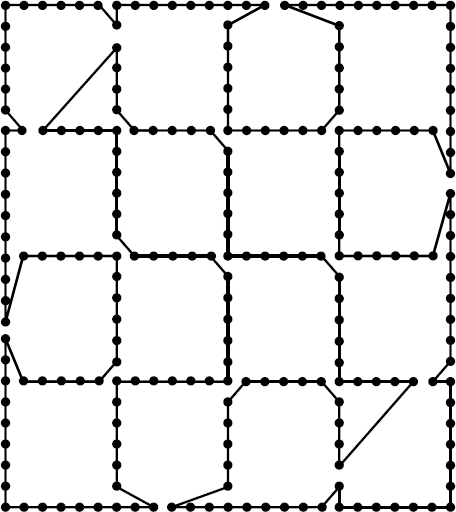
“这样看上去这个问题非常简单呀。”
“呵呵,事实上对称性也许让这个问题变得更加困难了。因为所有东西看若都差不多,只会让我们更难选择切掉的分支。”
“那么世界纪录是 ”
“ 在不久之前还是这个。”
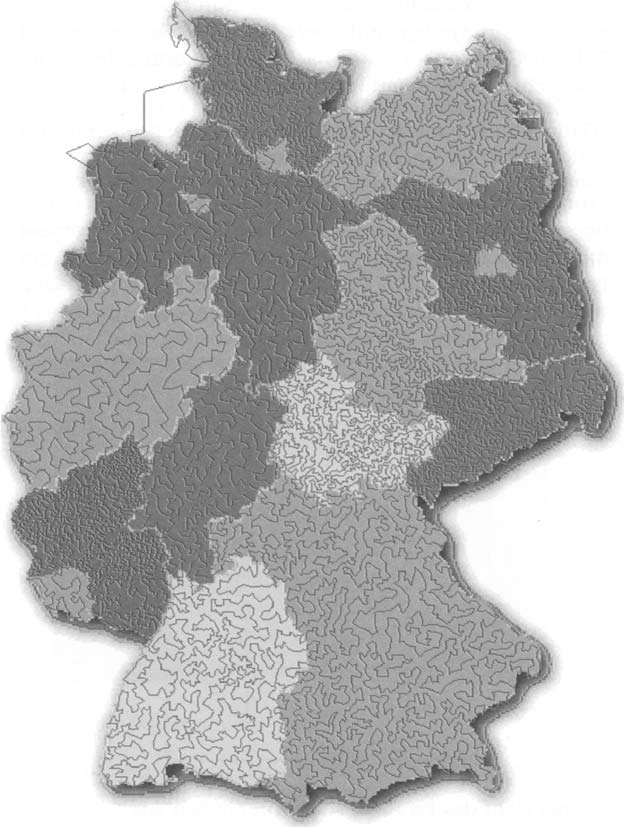
“这不正是环德国之旅吗?!”
“ 经过所有 15112 个城市。”
“太奇怪了! 怎么可能在莱茵兰– 普法尔茨州的城市数和在北莱茵–威斯特法伦州的城市数是一样的呢?”
“好问题。在莱茵兰– 普法尔茨州的居民数没有其他州那么多,但是这里的城市要小得多。在鲁尔区当然有很多大城市,但是并不意味这个地区的城市就比较多。”
“不久之前?”
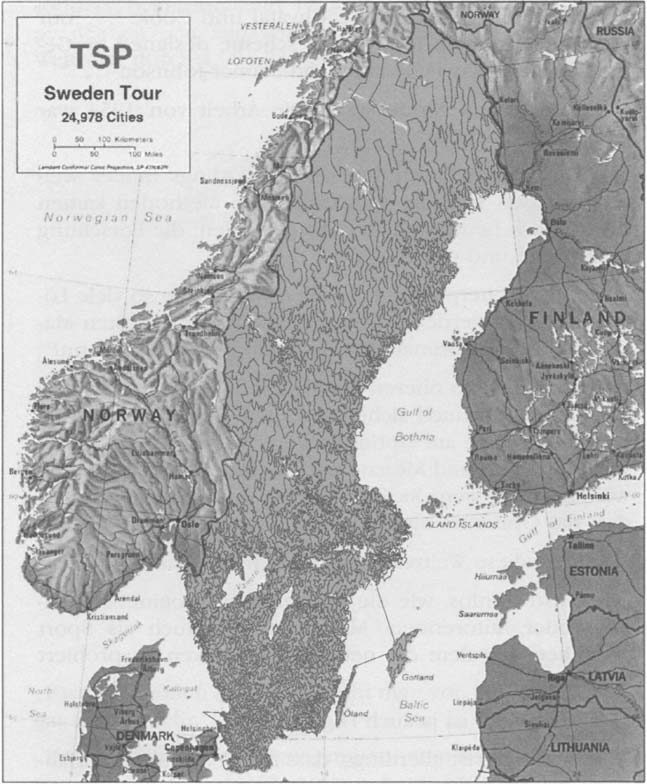
“从 2004 年 5 月开始有了一个新的世界纪录: 一个经过 24978 个瑞典的地点的环游。”
 (图片来源: Applegate,Bixby,Chva´tal,Cook 2001,http://www.math.princeton.edu/tsp/history.html)
(图片来源: Applegate,Bixby,Chva´tal,Cook 2001,http://www.math.princeton.edu/tsp/history.html)
“24978 个瑞典的地点? 瑞典的人口数也不过几百万而已。”
“只要居住人数超过三个人的地方都可以被称作地点。”
“相比之下那个 49 个城市的问题就像是小孩子的游戏一样。”
“从 1954 年以来,组合运筹学有了很长足的发展,但是即便如此,四位世界纪录保持者 Applegate,Bixby,Chva´tal 和 Cook 说: ‘我们的计算机程序依据的是由George Dantzig,Ray Fulkerson 和Selmer Johnson 设计的框架 ’。”
“所以不是小孩子的游戏。在 1954 年的这个工作真的非常重要!”
“对。从那时候开始,各种技巧一直在被简化,而且很多新的方法也不断出现。现
在依然有很多未解决问题; 关于这个问题的研究还在不断前进。”
“如果我想要制造一个需要打那么多洞的集成电路,最好的数学家也没有办法找到最优的结论,那么能怎么办呢?”
“通过上界和下界的帮助,我们经常已经可以保证找到一个几乎最优的选择。没有任何一个公司会花上几个星期甚至几个月的时间来尝试找到一个最佳方案,如果他们知道只需要短短的时间就能找到一个和最佳方案只相差百分之几的方案。”
“所以对于世界纪录的追求在这方面来说是完全没有意义的。”
“与对于游泳或者驾驶速度的世界纪录的追求一样。我们可以将这个理解为一项运动,不断尝试新的技术和突破。”
“明白了,一级方程式赛车也是一项高科技运动。”
“更重要的是,在这个过程中得到的经验和发展的方法可以在现实生活中帮助解决大的有意义的问题。上面提到的那个环瑞典的旅行只是至今最大的已经找到最优方案的问题。在 http://www.math.princeton.edu/tsp/world/countries.html 中你们还可以找到其他的国家的环游,有一些已经有了最优方案,有一些只是列出了至今找到的最好的解答。例如,经过坦桑尼亚的 6117 个地点的最佳方案还是未知的。特别值得注意的是,在 http://www.math.princeton.edu/tsp/world/index.html 中提出的经过 1904711 个地点的环游世界之旅的最优方案的寻找。”
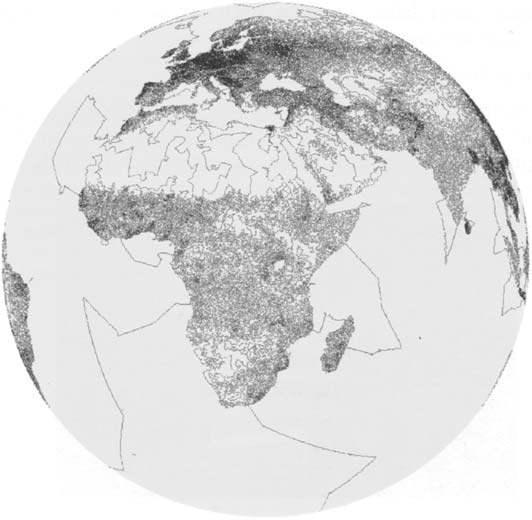
“将近两百万个城市; 在这种旅程之后我们几乎没有没看到的地方了。”
“为了追踪这样的一个旅程,我们必须考虑一系列局部的放大。这样找到的旅程很有可能并不是最好的,但是我们总是可以证明,它和最优方案的差距不会超过 0.068%。”
“哇,简直无法想象在一个有这么多城市的问题中,我们可以和最优方案距离这么近 ”
“ 而且我们可以证明!”
“Ruth,你不觉得我们应该结束了吗? 你还需要打包,而且明天我们想要尽早出发。”
“你说得对。”
“好吧,那么我现在也该回家了。我明天需要几点来接你? 大约 9 点?”
“很好! 我很开心! ”
施坦贝尔湖的旅行真的非常快乐。很多阳光,一趟航海旅行,有音乐的野餐; 一切都是那么美好。
 MSI 弗雷莱辛
MSI 弗雷莱辛
大概在中午的时候,又出现了一些悲伤的情绪。他们已经三个星期没有见到面。Ruth 已经开始想念 Jan 了。Vim 也缺少了他们两个人的陪伴,但这完全是另外一回事。
附注:本文选自《来自德国的数学盛宴》(http://www.landraco.com.cn/index.php/product-26213.html)
| 作者: | Peter Gritzmann,René Brandenberg |
| 译者: | 邱予嘉 |
| 文章来源: | [德]贝伦兹/格雷兹曼/齐格勒编著,邱予嘉译,《来自德国的数学盛宴》,高等教育出版社,2017。 |





