总统选举过程
美国人每四年选一次总统。投票和选举对一个有效的民主制度而言是必不可少的。人民选出他们的代表来治理国家,而这些代表制定和执行每天都在影响人们生活质量的法律。今年,美国数学宣传月让大家更加了解数学和统计在理解投票和选举时所起的作用。
美国总统选举的过程非常复杂。几乎就在新总统当选之时,下届选战就又要开始了。候选人要自我定位,筹集竞选资金,并在广泛的时间里开展这些运动。在正式参选前,要经过预选、初选、辩论等步骤。
这里有三次总统选举的结果,只显示获得相当数量选票的主要政党和其他候选人的结果。
| 年份 | 参选人 | 票数 |
|---|---|---|
| 2000 |
小布什(George W.Bush)
|
50,456,062 |
|
戈尔(Albert Gore, Jr.)
|
50,996,582 | |
|
纳德(Ralph Nader)
|
2,858,843 | |
| 1992 |
克林顿(William J.Clinton)
|
44,909,326 |
|
老布什(George Bush)
|
39,103,882 | |
|
佩罗(H.Ross Perot)
|
19,742,240 | |
| 1968 |
尼克松(Richard M. Nixon)
|
31,785,148 |
|
汉弗莱(Hubert H. Humphrey)
|
31,274,503 | |
|
华莱士(George Wallacet)
|
9,906,473 |
一个有趣的问题是,这些数字是否像报道时出现的一样准确。有此疑虑是因为大多数人如被要求计算看似确定的数字时,往往会得不到正确的答案。(通常这是因为进行大的计数时要花很长时间,这会导致我们的注意力衰退,也因此可能会作出一些错误。)
计票的准确性问题,由于著名的2000年总统大选中佛罗里达州涉及到的计票“吊挂式”问题而凸显而出。如果你看不同的信息源,就会发现小布什和戈尔在2000年大选的总得票数居然不一样。大多数人只想到列表显示纸质选票,对网上电子投票的计票结果的准确性提出了很多问题。数学家和计算机科学家正在探讨投票和计票结果准确性和安全性的问题。特别是,假设我们有部分选举结果并且得到某些特定地区的投票准确性,我们可以确定这些选举结果会否受有争议选票的影响吗?这里值得注意的是,在2000年得到最多选票的候选人最终并没有成为总统。由于总统的选票只允许投给一名候选人,很难知道两个最后竞争者之间出现的投票结果会否和初选时多位候选人竞选的后果一致。此外,我们不能肯定,选民投赞成票的候选人是否是该选民“最爱”的候选人。例如,在2000年大选中,有可能某些选戈尔或小布什的选民可能更想选纳德,但他们还是投了和自己愿望相反的票,因为鉴于票计算方式,他们并不想废掉自己的选票,即不想把自己的一票投给明显的弱者。
选举团
戈尔在2000年没有赢得选举的原因是总统选举不是按选民投票数,而是按选举团投票数的。选举团工作方式的本质是,美国50个州的每个州投下一堆票,这些票数代表了该州的参议员总数(总是2)和该州在众议院拥有的成员数目。哥伦比亚特区的选举团也有3票。因此,总共有100+435+3=538票,要当选总统(副总统随总统自动当选)则需要270票。
在1988年的选举中,老布什获得的选举团票数为426(79.2%),而迈克尔·杜卡基斯则得到111张票(20.6%)。从这个数据,你可能会认为老布什以“压倒性”优势赢。然而,老布什获得民众的48866097张票(53.4%),而杜卡基斯得了41908074张票(45.6%),这表明二者的选民选举结果比较接近。
选举团投票与民众投票在上例的差别表明,候选人试图获得当选总统的方式,不仅取决于候选人得到多少票,而是这些票在哪些州获得。这导致他们决定如何花费自己的时间及如何花钱才能当选成功。数学家已经通过研究加权投票试图洞察选举团和拥有大票源的投票机构的作用。加权投票不仅用于选举团,而且在欧盟事物中也起着调节所用,这是由于欧盟不同国家拥有不同的人口规模和经济实力。有些人认为,省去选举团的民众一人一票选举将会更加民主。也有些人辩称,如果没有选举团并且国家有一个“更好”的投票制度,美国不必只有两个主要政党而可能会有更多政党,因此选民有更多的选择。还有人说,如上所观察到的,民众投票票数接近往往转化为选举团的巨大影响,而这将增加国家稳定性和美国式的民主。
要成为总统还有一层复杂性:获得两个主要政党(民主党或共和党)之一的认可。主要政党总统候选人的选择是通过预选和初选的复杂系统来运行的。一个很好的例子是在2008年大选中关于相对小的州对候选人的当选的影响不成比例的关注,因为这些小州初选与大州相比来得更早。这导致密歇根州和佛罗里达州这两个大洲决定提早安排他们初选。然而,民主党决定不允许在这些重组初选选出的代表“坐”在它的党代表大会上。在选择候选人过程中, 如何平衡全国不同地区的选民的影响是一个复杂的问题;这个问题也引起了不同学科学者的兴趣,他们都试图用巧妙的数学方法来解决最佳决策问题。
选举及投票的数学洞见
美国人不仅投票选举总统,也投票选举制定国家法律的国会代表。这些代表用投票来制定这些法律。选举和投票的行为在民主政体中根深蒂固。选择高中典礼的演讲者需要投票,工会野餐中需要什么也要投票,哪个运动员应该赢得年终最佳投手奖以及哪个电影女演员应该得奥斯卡最佳女配角奖也都需要投票。
选举和投票也许是政治学的传统领域。然而,人们越来越清楚地发现,数学家和统计学家关于如何设计和提供投票系统,以及在不同投票系统之间的利弊权衡方面,都可以提出重要的建议。
投票和选举在一个非常复杂的环境中进行。当数学和统计在这些情形下应用时,人们给出所研究情形的简化假设——这一过程称为数学建模,它试图洞察问题的本质到底是怎么回事。
一个投票系统有:
- 作出选择的投票者
- 候选者
- 如何处理候选者(例如,一个胜者,几位胜者,及顺序等)
- 投票方式
- 决策方法(例如,如何收集选票数,如何选择委员会成员等)
选举系统的这些部分中的每一项都带有各种各样的复杂性。例如第一项,谁应该被允许在选举中投票?只有男人?只有那些拥有财产的人?只有18岁以上并且没有犯重罪的人?作为选举制度的一部分,人们必须对这类问题作出决定。事实是,就在100年前,妇女在全国性联邦选举中是没有投票权的。美国宪法1920年核准的第19条修正案才赋予妇女投票权。同样,哪些人可被作为候选者可能更复杂。为了获得选民可能的选票需要一个获得提名的复杂系统,避免选票被不认真的候选人或那些完全没有当选机会的人搞乱。
投票方式
为简单起见,我们将考虑这些投票情况:选一个单一的赢家或构建一个排名。比如“投票”决定邀请谁作为大学毕业典礼演讲者时要对候选人排名,因为排名最高的可能在规定的那天无法参加,这时备用人选就非常重要。现在,当考虑选民的选票时,从数学的角度来看事情则变得较为有趣。选票是选民自己对候选者偏爱与否的一种表达。
任何投过票的人都熟悉标准投票:提供一个可选者名单(有时给出更多的选择机会),选民从中必须选一个。在本文开始时指出的总统选举表明,有些人对已经实施的标准选票和投票系统不满:当有两个以上的认真且知名的候选人时,往往有些人可能会觉得他们并不代表“人民的意志”。
试想一下,你面对表达你对公司野餐中比萨(P)、沙拉(S)、汉堡(B)的感觉这一问题。为了方便起见将这三种选择用P、S和B来表示。你可能同意,在标准投票中仅说你想S。但你更倾向于投沙拉后,表达第二个选择为B然后是P。你可能事实上对比萨过敏,但与当人们说他们对竞选总统的候选人过敏或者说从来没听说过某个候选人相比,这两种候选者的重要性是完全不同的。
这种思考已经产生了对多种投票方式的兴趣,其中有些想法仅仅最近才被认真地研究过。下面是对一部分这些迷人想法的简要介绍。
在最早的建议中有:选民对每一对候选人X和Y产生序号或排名,指明他们是否偏爱X或偏爱Y,或者对两者不偏不倚。有可以用来显示这种偏好的各项约定,但我喜欢在理解投票和决策现象中,使用基于数学思想的先驱Duncan Black所普及的符号。Black的想法是画一个向上的箭头,朝上方的是排名较高的选择。当排名两个可选者时,我们有三种可能性(如图1所示):
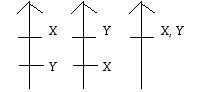 图1
图1 注意,当候选者的数量增长时,由一个单一选民投出的潜在选票结果数目会快速增长。如果我们有三个可供选择而无投票者不偏不倚的可选者,选民可以使用6种不同的选择来表达自己,而如果不偏不倚是允许的,那么选民可以有13个不同的选择来表达自己。没有不偏不倚的话,n个候选人的选票可能性是n!(即n的阶乘)。有一个严重的担忧:选民是否对超过4个可选者能够产生这些选票?这导致了这样的问题:如果使用这种选票,选民将被迫产生涉及所有候选人的选票,还是选民可以截断选票?截断意味着,比如说虽然有可供选择的6名候选人,选民在投票时只选择投3名候选人。
如果选民在X和Y之间更喜欢X,有没有某种方式来表达这种偏好的力量,而不是只为了表明宁要X?这方面的关注产生了可以表达偏好强度的基数选票的想法。为简单起见,假设有三位候选人X、Y、Z,希望让选民表达关于候选人的感觉强度。做这事的方法之一是给每个选民一个固定数量的点数,比方说100点,并要求选民使用所有这些100点,按选民认为合适的方式分配给三名候选人。例如,如果一个选民给X是49点,Y是48点,Z是3点,而另一位选民赋予X35点,Y34点,Z31点,则这两个选民将有相同的序号选票,但都有不同的选票基数。有一些人会问是否从这些数目得出Y比Z被这两个投票者更偏爱多少的结论。
基数选票的一个完全不同的方式是给点数挑一个数字(通常是0到100),并指定每个候选人从0到100的一个数字。这样,第一个选民可能给X100分, 给Y99分,给Z33分,而另一个选民会给X9分,Y8分,Z7分。我们再一次看到这两个分配有相同的序数选票。这些点数的确切含义还不清楚;点数是否对不同的人具有不同的含义这一点是有问题的。毕竟,在街上见到20美元对无家可归者和百万富翁意味着不同的东西,虽然都是相同的20美元钞票。这种类型的选票已经与一个称为范围投票的投票方法相关联。
除了这里各种不同的序数和基数投票,简单地说还有一些其他的想法:
a. 连记投票:投所有你看中的候选者。
- 注:在1970年的大约同一时间,有几个人开始讨论使用新型的投票法和决定选举的联合系统。Guy Ottewell, Robert J. Weber, Steven Brams,和 Peter Fishburn 这些人突发奇想到这样的投票方式:虽然只选择一位可选者,人们应该有一种投票法可以考虑可多可少的候选人。例如,如果一个俱乐部试图在比萨(P)、鸡(C)、汉堡(B)、鱼(F)和沙拉(S)之间进行选择,一个选民可以同时投票给C和F。
b.“是-否”投票:对每个可选者投“是”或“否”。
c. 混合投票:将可选者分为两组。你因为了解第一组的人而提供你的有关资讯,而对另一组,你毫不知情。在表明划分两组候选人后,人们可以就他们所熟悉的那组候选人进行排名或核准。
连记投票是特别有趣的,精通数学的政治学家Steven Brams已经在最近真刀真枪的选举中推动使用连记投票,并取得成功。
 Steven Brams
Steven Brams Brams的成功鼓励了其他改革者试图游说改变美国目前的选举制度。Brams(有时与他人合作)也产生了大量有趣的与投票理论及投票和博弈论之界面有关的“自相矛盾”的例子。他出版了许多书籍,探索迷人的数学与表决和选举接口,以及更一般地与公平问题的接口。
决策方法
采取了一个投票方式后,需要寻找很好的方法来基于所选类型投票方式决定赢家。再次,为简单起见,我们考虑序数(排名)投票的选举,在其中每个选民对所有候选人排序,没有对于两个或两个以上候选人的不偏不倚。如果只有两个可选者,情况很简单。每人选其最喜欢的那个可选者,而决策系统则宣布赢家是获得票数最多的人。(如何打破选举中的平手僵局是一个重要的课题。为了简化这里的讨论,我将假设没有平局发生。这是选举中的一个合理假设,因为有大量的选民。)当有两个可选者时,获得票数较多的人得票将过半数。但是,只要允许超过两个可选者,通常的投票可能会导致没有候选人获票过半数。在这种情况下的通常决策方法是使用复数投票,获得票数最多的候选人是赢家。
一旦使用排名投票,有许多被建议的方法来决定选举。虽然下面的选举不是这种类型中的最小例子,我将用它来说明一些有关选举决策在选举数学研究中已出现的方法。
当人们看到排名似乎提供有关选民检视候选人的微妙方式的附加信息,他们想当然地认为自己的这些选票将指挥“最佳”、“最公平”或最“理想”候选人的选举。然而,事实证明,给出这种选票的集合,选举的赢家取决于决定赢家的抉择方法。当一个人在现实中生活足够长后,这似乎并不很奇怪,但它总让第一次看到它的人吃惊,因为我们的信仰是人民的意志让我们对社会有正确的选择。
考虑这个选举:
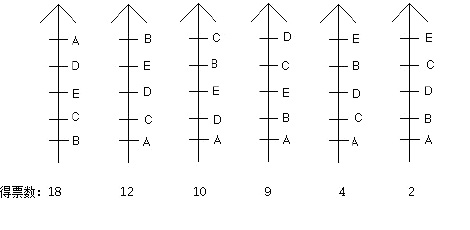 图2:一个选举涉及55个选民
图2:一个选举涉及55个选民 这个选举中有5名候选人,并有55个选民。在进一步阅读之前,你不妨来决定如果只有一个赢家被选出,你认为谁应该赢得这场选举。在这里谁是人们的选择?
如果使用复数方法,胜者将是获得18/55=总票数的32.7%的A。有一个“更好”的方法吗?这“更好”词的麻烦是,人们需要一种尺度来比较不同的方法,而几乎没有任何一种被公认的尺度。通常情况下,如果改变一个系统,总有些人从变化中受益,而另一些人则受损。在有许多候选人的选举中,一直有一种担心认为各候选人的票的分裂可能会导致某个人“勉强”成为并没有得到广泛支持的当选者。一种弥补的方法是在没有人得到总投票数过半数的情况下举行某种形式的决胜选举。决胜选举呈现这几个问题:
- a. 花费额外经费去运行,往往在决胜选举中投票者比第一次选举少得多。
- b. 关于如何举办决胜选举有许多形式。
序数投票的优势之一是它允许决胜选举,而无需选民返回投票站。但是请注意,当原先的选举后运行决胜选举时,至少有一些选民在随后的期间对有关候选人的喜好很可能已经改变。然而,带着如图2所示的偏好,我们可以举办无需选民返回投票站的决胜选举。
关于怎样进行选举的巧妙构思确实已在几个世纪前提出,而千百年来,许多用于选举的新颖和吸引人的系统已被提出。通常情况下,这些方法以这样 的“解释”出现:它们是值得的、优越的、公平的,或比以前的方法更加民主。在这里,我们提请大家注意一个事实,即选民通过自由前往投票站和他们的选票被清点无误的这些事实而得到的民主感觉,是天真的。要看到这一点,我们只需要看看5种方法的一个样本,它们只是可被用在序数投票的许多合理和有吸引力的方法中的一小部分。
在这里我们考虑:胜出票数、决胜选举、顺序决胜选举、波达计数法和孔多塞。
a. (胜出票数)谁得到第一名选票的数量最多的候选人是赢家。
b. (决胜选举)如果没有候选人获得过半票数,得到第一名选票数最多的两名候选人留下决战。
c. (顺序决胜选举)如果没有候选人获得过半数,消除第一名选票最少的那个候选人。以这种方式继续,每次消除第一名选票最少的人,直到剩下两名候选人为止。
d. (波达计数法)我们根据他们怎样被一个选民的选票排名而给候选人分数。候选人X从某个特定选民得到的票数是那张选票上低于X的候选人人数。
举个例子说明这个计数法。对如下所示的选票(图3):
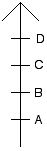 图3
图3 候选人D得3分,候选人C得到2分,候选人B获得1分及候选人A得0分。如果本次投票有7个选民投票,则候选人C得到的分数将是7乘上2,即14分,而B得到的分数则是7分。
e. (孔多塞)如果有候选人在双向竞争中击败其他候选人,该候选人当选。(比如两个候选人X和Y之间的双向竞争,我们看到是否更多的选民在X和Y之间更偏爱X,或反过来。)
我们可以用一点点组合学来看在上述选举中有5位候选人时有多少双向竞争。这涉及到在5个东西中取2个的组合数,而不考虑选两个东西的顺序。这个数字用著名的二项式系数计算。这里,以无序方式从5件东西中选两件的选法个数是10,所以5名候选人时有10种双向竞争要考虑。我们可以用一个二合图(有向图)来记录双向竞争的信息,如图4所示。这种有向图被称为比赛的有向图,因为它们可以解释哪支球队在体育比赛中击败对方。对于图2的选举,在C和B之间的双向竞争中,我们看到C打败B。可用画在代表了双向竞争的图中(图4)从C到B的双向箭头来表示。我们还可以在标记为C的行和标记为B的列交接处写上偏爱C的选民数(39),并在B行和C列的交接处放上喜欢B的选民数(16)。图4和表1中的其他箭头和数字,以类似的方式落实到位。
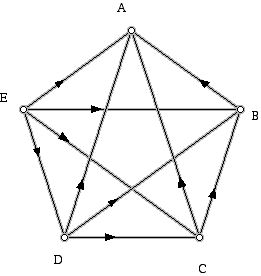 图4
图4 | A | B | C | D | E | |
| A | - | 18 | 18 | 18 | 18 |
| B | 37 | - | 16 | 26 | 22 |
| C | 37 | 39 | - | 12 | 19 |
| D | 37 | 29 | 43 | - | 27 |
| E | 37 | 33 | 36 | 28 | - |
将上表中的每行数字求和。你认识这些和数吗?他们原来是选举的波达计数值!
例如,候选人B的波达计数值如下所示:
这是第二行的行和!
在描述孔多塞方法时,我曾谨慎地说,应该选在双向竞争中击败所有其他候选人的那个候选人,假设这样一个候选人存在。令人意外的是,有这样的选举,在那里没有孔多塞赢家。一般来说,如果A比B较重且B比C较重,则A比C较重。“较重”是数学家称之为传递的关系;我们往往在现实生活和数学中熟悉的许多关系是传递的。然而,赢得序数投票上的双向竞争违反传递律,如下面的例子(图5)所示。
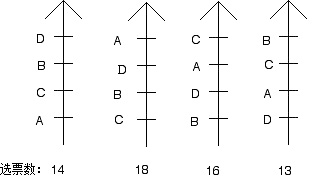 图5
图5 你自己验证:在一个双向竞赛中A打败D,在一个双向竞赛中D击败B,在一个双向竞赛中B战胜C,然而,在一个双向竞赛中C赢了A!这种现象被称为“孔多塞悖论”。如果这次选举的赢家由一序列双向竞争直到作为最后一名胜利者而出现,那么,依投票的顺序而定,任何可选者都可以成为赢家。政治学家们认为,这种现象可能实际上已经发生,如美国众议院的投票机构的例子。
因此,如果没有孔多塞赢家,支持“孔多塞思想”的话就需要在这种情况下选择一个赢家。这样做有很多方法。例如,Duncan Black 建议如果没有孔多塞赢家,则波达计数应被用来挑选一个选举的赢家。
使用这5种不同的方法谁是赢家?你会惊讶5种不同的方法导致5种不同的赢家吗?
复数选举赢家是A,决胜选举赢家是B,顺序决胜选举赢家是C,波达计数选举赢家是D,以及孔多塞选举赢家是E。因此,如何计算票数与选民的投票决定赢家的选择。
几个用来决定选举的方法使用相对基本的算术,用相对初等的数学工具。然而,事实证明,使用与社会选择理论和选举理论非常不同的问题激发起来的数学方法,可以得到很多洞见。这样的例子可以在Donald Saari和Gil Kalai的工作中找到。特别是Saari借助于动力系统理论,帮助阐明与孔多塞悖论相关的问题,并已取得关于投票理论的戏剧性的洞见。动力系统是数学的一个分支,它更经常地用于了解行星和空间飞行器轨道计算的问题,而不是有关选举的问题。Saari还试图表明,有些情况下,投票数的小变化可能导致排名候选人方式的大变化。
 Donald Saari
Donald Saari 公平性的公理化处理
如果利用某些利己的合理特点用来确定选举的决策方法,则可以产生不同的获奖者。那现实中我们到底应该使用哪一种方法?如何看待公平问题的一个重大突破由具有数学训练的经济学家阿罗(Kenneth Arrow)给出,阿罗也由于他的路径搜索工作荣获诺贝尔经济学奖。他的基本策略是搞清楚一个好的选举方法应遵守哪些公平属性,而不是只研究个别方法有什么不错的功能。
 Kenneth Arrow
Kenneth Arrow 运用初等数学,阿罗令人惊讶地证明,如果有3个或更多的可选者,每人选择一个排名,则没有一个选举决策能服从一个合理短名单下的所有公平条件!随着阿罗的开创性工作,现在有越来越多的公平条件被提出,试图确定哪些选举方法可以满足其中哪些公平规则。在这一领域的黄金标准是要找到一组只能由一个特定的决策方法M满足的条件。当一个人获得一组成功的刻画(例如,一个决策方法必须是方法X,当且仅当它服从某些给定的公理或公平规则),那么当在两个不同方法之间切换时,就有可能看到权衡。
很多人认为,阿罗定理的意思是它不在乎我们采用哪种选举决策方法,因为没有完美的方法。相反,阿罗工作的重要性是,它给人们一种比较和对比不同方法的框架,这样人们可以了解每个方法有什么属性以及没有什么属性。有这么多理想的公平规则(当有至少三名候选人时),但没有任何方法能满足所有的这些规则。总而言之,人们可以清楚地看到不同方法的缺点和长处。
经济学家为什么对投票感兴趣呢?在经济学中,规划师通常有必要决定哪些经济政策中需要实行。有时这个决策的框架被称为集体决策,它实际上提出了选举和投票中的同样问题,因为决策者会为了一组人的利益而选择最佳候选者(这里也许是经济运行的方式)。因此,人们正在寻找一种取决于个人选择的社会选择。因为对集体决策的开创性工作,阿罗被人们尊称为社会选择理论之父。
投票系统的操控
理想情况下,人们希望投票方式具有这样的属性:如果选民事先知道计票的方法以及有关其他选民可能会怎样投票的信息,他们则会诚心诚意地投票。诚心诚意的意思是选民只根据自己对候选者的看法来填写选票。选民不考虑通过与候选人本身无关的信息来改变投票人试图得到一个更好结果(例如,投给排名较高的候选者)。
假设选民知道波达计数法将被用来决定选举。如果该选民的真诚选票是:
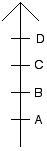
则这个选民知道在选举中,这将给D贡献3分,给C贡献2分。如果D和C实力相当,这2点可能会导致C在选举中获胜而D在选举中落败。但是,如果选民如下投票:
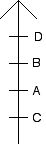
D依然得到4分,但现在C将得不到分。这样D赢的可能性就很大了!这个例子显示如果用波达计数法,一个选民相对容易倾向于投一张言不由衷的票。
与选民获得信息有关的投票过程有许多理论和实践结果,尤其是在像延伸横跨多个时区(缅因州到夏威夷)的国家。如果夏威夷(人口少的州)或加州(美国各州中人口最多的)的选民知道美国东海岸的票站调查结果,这将如何影响他们在总统选举中的投票态度?此信息可能会导致部分选民投票言不由衷或以其他方式改变他们的投票行为(比如选民可能决定留在家里而不去投票,因为该选民认为所支持的候选人当选无望了)。
鉴于这些考虑,这里很自然要问什么样的计票方法不允许操控投票过程?这类问题的答案是由Allan Gibbard和Mark Satterthwaite率先独立给出的。Gibbard和Satterthwiate表明,对于有三个或更多可选者的投票情形,在非常弱的假设下,不可操纵的唯一决策方法是独裁!(独裁是这样的选举规则:无论任何其他选民的选票怎样,结果总是符合一个人的选票,即独裁者的选票。)这个结果的重要性和深刻性不亚于阿罗定理,具有非常重要的关于投票和投票行为的结果。它提出如下这些重要问题:在选举中提供给其他选民非常详细信息的后果,以及那些容易利用其他选民行为的方法来改变选举结果。有趣的是,Gibbard本科学的是数学,而研究生读的是哲学,而Satterthwiate本科和研究生期间都学习经济学。他们的工作已经打开研究决策中信息的价值和作用的闸门。连同阿罗定理,Gibbard-Satterthwiate定理在指导投票和集体决策时是一个巨大的支柱。
 |
 |
| Allan Gibbard | Mark Satterthwaite |
谁研究公平、投票和选举?
虽然投票和选举专家应该属于政治学家,但正如我们所看到的,政治学家在里面起的作用仅仅是一部分。从18世纪的改革者开始,许多人都想去完善投票和选举,并为此作出出重大贡献,其中有许多国家、不同时代和不同背景的人士,包括Arrow, Borda, Michel Balinski, Condorcet, C. L. Dodgson (Lewis Carroll), Allan Gibbard, John Kemeny, Hervé Moulin, Donald Saari, Mark Satterthwaite 以及 H. P. Young.他们属于不同的专业和国家,但共享一个目标:用数学的力量去研究公平问题。
参考文献(略)



