编者注：
本文选自科学出版社 1981 年出版的《物理学的方向》（狄拉克/著，张宜宗、郭应焕/译）第一章 量子力学的发展。在此，对所录引文的译者和出版社表示感谢。

我非常高兴地到悉尼来，并且能有机会向你们作报告。我想谈一谈关于量子力学的发展。虽然这些发展在我之前实际上已经开始，但我亲身经历了许多这些发展。量子力学是在牛顿经典力学的基础上发展起来的。牛顿建立了他的力学定律，从此这些定律就支配了整个的力学理论；并且我们发现，在用爱因斯坦的相对论作某些必要的修正后，这些定律与许多大尺度的观测结果仍符合得很好。只要把这些定律用于宏观物体，就能得出正确的结果。但当人们把这些定律用于微观物体，例如原子世界时，这些定律就完全失效了。

我们称之为经典力学的牛顿力学是我们的出发点。利用麦克斯韦理论，我们可以把这个经典力学运用于描述电荷（带电粒子）的运动。但我们将看到，我们所得到的结果并不适用于原子。

已经建立起来的原子模型是：原子有一个带正电的核心，一个或几个电子围绕着这个核心不停地运动。根据牛顿力学和麦克斯韦电磁学（当把它们应用于电子的电荷时），这些电子由于辐射要逐渐地损失能量，最后要坍缩到原子核中去，因此原子决不会是稳定的，而通常我们知道原子是稳定的，这就产生了矛盾，当然这个矛盾最初曾使人们非常困惑不安。

玻尔首先得出对这个矛盾的解决办法。他提出，我们必须假定原子可能有某些稳定的状态。在这些稳定态，它不发出辐射。这意味着把经典力学应用于带电粒子时必须假定与牛顿力学标准方程有一个偏差，即不得不忽略与辐射发射有关的那些力。但这些力是很小的，它们在一级近似中无关紧要。重要的力是电荷之间的库仑力。按照波尔的假设，我们必须对一个原子中电子所遵守的运动方程作出这种近似，并且还必须假定原子只能在叫做稳定态的某些态中存在。这些态是用与经典力学完全不同类型的一些条件确定的。这一组新的条件叫量子条件，其中包括普朗克常数（用 $h$ 表示），这是普朗克在他的黑体辐射定律中发现的一个常数。

玻尔建立了这样的原子模型理论，在这个理论中，原子以稳定态形式存在，并且服从量子条件。按照玻尔理论，一个原子能够从一个稳定态跃迁到另一个稳定态，在跃迁过程中，原子要发射〔或吸收）辐射，以保持能量守恒。这个被发射或吸收的辐射是具有一定频率（与能量有关）的单个量子。

这些槪念和牛顿力学告诉我们的概念完全不同；满足特定条件的稳定态的概念是非常新的概念。在解释氢原子光谱和只有一个电子起重要作用的其它简单原子的光谱时，人们发现玻尔的这些思想一直是非常成功的，这种巨大的成功使我们不得不接受玻尔理论。

我记得在我第一次听到玻尔理论时，我感到非常惊奇，因为以前在整个原子世界笼罩着一种神秘的气氛。当我在布里斯托尔上学的时候，我没有听到过任何有关玻尔这个理论的内容，只是我在剑桥大学当硏究生的时候，我才得知这个理论。当时这个理论打开了我的眼界，使我看到了一个新的世界，一个非常奇妙的世界。令人惊奇的是我们加上一定的条件后就能把牛顿定律用于描述原子中的电子运动。这些条件是：首先我们必须忽略作用在电子上的与发射辐射有关的力；其次我们必须引进量子条件。我仍然清楚地记得玻尔的这个理论当时给予我多么强烈的印象。我认为在量子力学的发展过程中，玻尔引进的这些槪念是迈出最伟大的一步。事实上，最出人意料之外的和最使人惊奇的是这种概念从根本上违背牛顿定律，但它居然获得了成功的结果。

后来人们对玻尔的理论进行了深入的研究，发现它的成功非常有限。从根本上说，在处理只有一个电子起重要作用的原子体系时，这个理论是成功的，但对于含有两个或两个以上的电子，如氮原子或别的更复杂的原子体系时，人们就不知道怎样用量子条件来确定它的稳定态。曾经作出过一些人为的假设，进行过各种各样的计算，但都未获得成功。在我研究原子理论的时候，就是这种状况。在那些日子里，我所面临的问题，就是每个人都在进行研究的问题，即“怎样才能够发展玻尔轨道的思想，以适用于那些更复杂的原子?”

1925 年海森堡取得了巨大的进展，他采取了一个非常大胆的步骤，提出这样的思想：物理理论应当集中在与观测量有密切关系的那些量上。既然，我们观测的一些量与玻尔轨道的关系只是非常间接的，所以海森堡认为玻尔轨道并不十分重要。所观测的量，或者与观测量有密切关系的量，全都是与两个玻尔轨道有关，而不是只和一个玻尔轨道有关；这里特别重要的是两个轨道而不是一个轨道。现在要问：这样会产生什么结果呢？。

假定我们考虑具有某种性质的、与两个轨道相联系的量的全体，并且要把这些量写出来。要写出一组量，其中每个量都和两个元素有关，通常的方法是用下面的形式：$$\begin{pmatrix}X & X & X & X & \cdot & \cdot & \cdot\\X & X & X & X & \cdot & \cdot & \cdot\\X & X & X & X & \cdot & \cdot & \cdot\\X & X & X & X & \cdot & \cdot & \cdot\\ \cdot&  \cdot &  \cdot & \cdot  &  \cdot & \cdot  &  \cdot\end{pmatrix}$$ 这种形式就是用行和列把一组量排列起来，人们把行与其中的一个态联系起来，把列与另一个态联系起来。数学家把象这样的量的集合称为矩阵。

因此，海森堡认为人们应当研究这样的一组量，并且应当把这组量的整个集合看成对应于牛顿理论的一个动力学变量。当然，这些动力学变量就是粒子的坐标，或者速度或者动量。根据海森堡的看法，每个这样的量都应当用一个矩阵代替。导致海森堡这样考虑的基本思想是人们应当根据可观测量来建立理论，并且这些可观测量就是这些矩阵的元素，每个元素都与两个轨道相联系。

在作矩阵计算时，人们能够将矩阵相加和相乘，并且能用矩阵构成一个代数。但是这样就得到一个新的、有用的重要性质，即如果把两个矩阵 $a,b$ 相乘，得到的积 $ab$ 与 $b$ 乘 $a$ 得到的积 $ba$ 一般并不相等。矩阵乘法有确定的运算规则。这些规则使得 $ab$ 与 $ba$ 的结果不相等，人们不能迴避这种规则。如果我们把动力学变量看作矩阵鼻这就盍味着动力学变量应当满足一个代数，在这个代数中，$ab$ 不等于 $ba$，这样的代数叫做非对易代数。

当海森堡最初注意到他的矩阵不满足乘法交换律时，对此他感到非常不安，他觉得也许就在这一点上他的整个理论要全归失败（自古以来，物理学家用的动力学变量总是遵守通常的代数乘法规则，即 $a$ 乘 $b$ 等于 $b$ 乘 $a$ 很难想像有不具备这种性质的动力学变量），海森堡对此感到不安是很自然的。但这却是他的理论的基本点，而且后来证明是最为重要的一个关键。实际上，海森堡新力学的一个最重要之点就是，动力学变量服从一个代数，它不遵守乘法交换律。

从海森堡的最初思想出发，人们就能在这方面取得相当迅速的进展。当时我正好是一个研究生，我十分庆幸自已生逢其时，使我有可能也加入这个行列。

你们知道，我们所面临的问题就是要改变牛顿方程，使它适合于 $ab$ 不等于 $ba$ 的一个代数。乍看起来，这似乎相当困难：但是利用哈密顿一百年前做的一些工作，就使这个问题的解决变得容易多了。哈密顿研究了牛顿方程，他找到了表示这些方程的另一种方法。由于拉格朗日和哈密顿找到另一种表示方法，所以才有表示这些方程的一种普遍方法，这些方程叫做方程的哈密顿形式。哈密顿在建立方程的这种形式时，只是受了数学美观条件的影响，他也许会说：“用这种方法表示的方程是非常美妙的，不过并没有真正的必要这样做，如果你愿意的话，你可以继续用原来牛顿给出的那种形式的方程。”

但是看来哈密顿对什么东西是重要的有一种卓越的见解，我认为这是一个数学家曾经有过的最杰出的见解之一。他所发现的表示力学方程的这种形式，其重要性在一百年以后，也就是在他逝世以后很久，才为人们所认识。

方程的哈密顿形式的重要性在于很容易把它稚广以引进非交换性。人们能够用某种括号表达式写出哈密顿方程，这种括号表达式称为泊松括号，通常把它写为 $$[a , b],$$（这里我不写出这个括号表达式的定义，我只是要说明：这个括号出现在哈密顿形式的方程中，并具有十分重要的意义，结果证明这个括号表达式，即泊松括号，相当于（或非零类似于）$a$ 乘 $b$ 减去 $b$ 乘 $a$ 再除以 $-1$ 的平方根与一个确定的普适常数 $\hbar$ 的乘积，即相当于 $$\frac { a b - b a } { \sqrt { - 1 } \hbar }\tag{1}$$ 式中的 $\hbar$ 等于普朗克常数 $h$ 除以 $2\pi$ 用对易子 $ab-ba$ 代替哈密顿方程中的泊松括号，按照这个公式，能够立即把一切经典力学方程（将它们变为哈密顿形式后）变成服从非交换乘法的新型方程，这样我们便能把它们应用于量子力学的海森堡形式。

于是这便成为一种有趣的游戏，利用普遍的公式 $[a , b] \rightarrow \frac { a b - b a } { \sqrt { - 1 } \hbar },\tag{2}$ 亦就能把以前牛顿理论中动力学体系的各种模型变换成海森堡的新力学模型。

我们说这是一种游戏，一种大家都能玩的非常有趣的游戏，这样形容是不错的。那时，每当人们解决了一个小问题，就能对此写出一篇论文。在那些日子里，任何一个第二流的物理学家去做第一流的工作，都是非常容易的。但从那以后，一直没有出现过那样令人愉快的时期。现在第一流的物理学家做第二流的工作都非常困难。但在另一方面，我们却有可能比较容易地从牛顿力学的哈密顿形式过渡到海森堡的新力学形式，从而形成了属于新量子力学的方程。

这样，我们虽然有了包含那些非对易量的方程，但在起初我们对这些方程没有一个普遍的解释，这真是物理理论中少见的情况。（在任何物理理论中，人们在建立方程以前，一般都知道他的方程含意是什么，但在这里，就不是那种情况，我们已经有了方程，但还不知道如何运用它们。）

起初人们根据一些简单的例子进行推测，以后才逐渐地对方程作出解释。人们能够把相应于总能量的对角矩阵解释为其对角元素表示量子理论中各个态的能量。此后人们才逐步地去研究更普遍的解释方法。

我可以这么说，任何一个动力学变量都有一个普遍的运动方程。根据哈密顿的观点，任何动力学变量 $u$ 都随时间依下式变化：$$\frac {d u} { d t } = [ u , H ],\tag{3}$$ 式中 $H$ 是哈密顿理论中的总能量。我们看到它对应于下面的量子力学方程：$$\frac { d u } { d t } = \frac { u H - H u } { i h }.\tag{4}$$ 这样我们就得到了，在海森堡的新力学中，对于一个动力学变量就有一个普遍的运动方程。

我们必然要面临対这些新方程作出普遍解释的问题。薛定谔的一些工作对这个问题的解决起了很大的作用。薛定谔和海森堡当时都在独立地进行研究，薛定谔建立了自己的理论，即另一种形式的量子力学。乍看起来，这种量子力学似乎与海森堡的理论完全不同。薛定谔理论比海森堡理论发表得稍晚一些，但在几个月以后，就证明了他们两人的理论实际上是完全等价的，虽然他们两人的出发点看起来是很不相同。

薛定谔理论是以德布罗意的一些工作为基础而建立起来的。德布罗意指出了怎样才能把波和粒子二者联系起来，他提出了一个波函数，这个波函数通常表示为 $$\psi .$$ 单个粒子的 $\psi$ 也应是粒子的三个坐标 $x _ {1} , x _ { 2 } , x _ { 3 }$ 以及时间 $t$ 的函数，也就是 $$\psi \left( x _ { 1 } , x _ { 2 } , x _ { 3 } ; t \right).$$ 德布罗意就建立了一个用 $\psi$ 描述的波所遵守的方程。这个波动方程表明：如果有一些平面波在确定的方向上传播，并且具有确定的频率，那么这些浪便对应于一个具有确定动量和能量的粒子。这个对应是相对论性的对应，并且是数学上的一个精确的对应。德布罗意根据数学的美观性提出了波和粒子之间联系的思想。但他的理论只能应用于不受任何力作用的自由粒子。薛定谔推广了这个理论，使它能够用于在电磁场中运动受电力和磁力作用的电子。

在薛定谔的理论中，人们可以把算符（$-ih$ 乘上对 $x_r$ 的偏导数）作用在 $\psi$ 上，即 $$- i h \frac {\partial} { \partial x _ { r } } = p _ { r }$$$r$ 的值取 $1$，$2$ 和 $3$，并且每个这样的算符对应子一个动量算符。如果人们研究这样的算符，同时也研究 $x_r$，那么就是在研究与海森堡理论中的非对易量相类似的非对易量。在这个基础上，人们就能建立含有算符作用于其上的波函数的薛定谔理论与海森堡理论之间的联系。

在海森堡理论中，原来并没有出现波函数 $\psi$，通过薛定谔的工作，才把它引进了量子力学。后来人们发现波函数 $\psi$ 对应于一个态，也许就是玻尔理论中的一个稳定态。由于算符把一个波函数变为另一个波函数，算符就与两个态相联系了，这样，薛定谔理论与海森堡理论之间的等价性便建立起来。

在新力学的方程建立之后两、三年，才出现解释这个新力学的普遍方法，这个方法包括取这个波函数并构成它的模方 $$| \psi | ^ {2},$$ 而且认为是某个确定时刻粒子出现在给定位置上的几率。

在这里我引进了几率这个词，这意味着量子力学的普遍解释与几率有关。这个普遍解释能使我们计算出某一确定事件也现的几率。在这里的例子中，就是电子在某一时刻处于某一确定点上的几率。按照牛顿力学（即经典力学），我们恰好是不计算几率，而是精确地计算事件出现的时间和地点。新力学（即量子力学）不具备牛顿力学的这种确定性。这种缺乏确定性的情况是理解新力学的一大障碍，因为它很难令人接受。

当然，对原子所做的实验结果确与几率有关。根据新力学，我们能计算出这些几率，并能把实验结果与计算结果进行比较。我们发现计算和观测结果二者互相符合。由此看来，几率是人们真正需要的东西，不过人们对只给出几率的理论仍然并不感到满意，这便引起了一场很大的争论。

以爱因斯坦为首的一些物理学家认为：从根本上说，物理学应当是决定论的，而不应当只给出几率。然而玻尔接受了几率的解释，并且他能够使这种几率解释同他的哲学一致起来，这就引起了玻尔学派和爱因斯坦学派之间的一场大争论。这场争论一直贯串到爱因斯坦的一生。他们两人都是非常杰出的物理学家，问题是：“他们之中谁是正确的？”

根据公认的标准原子理论概念，似乎玻尔是正确的。以薛定谔波函数为基础的几率解解是人们能够作出的最好的解释。人们为改进这种解释作了许多的努力，力求获得比仅仅是一些几率更多的信息，但所育这些努力都以失败告终。根据现在的量子力学理论，玻尔所拥护的几率解解是正确的。不过爱因斯坦仍然是有道理的。他相信，正如他所说：“上帝不是玩骰子的”。他认为物理学从根本上应当具有决定论的特征。

我认为也许结果最终会证明爱因斯坦是正确的，因为不应认为量子力学的现在形式是最后的形式。关于现在的量子力学，存在一些很大的困难，这些困难我在后面还要讲，它是到现在为止人们能够给出的最好的理论，然而不应当认为它能永远地存在下去。我认为很可能在将来的某个时间，我们会得到一个改进了的量子力学，使其回到决定论，从而证明爱因斯坦的观点是正确的。但是这种重新返回到决定论，只有以放弃某些基本思想为代价才能办到，而这些基本思想我们现在认为是没有问题的。如果我们要重新引入决定论的观点，我们就应当以某种方式付出代价，这种方式是什么，现在还无法推测。

支配着新力学的基本方程及其解解的思想就是这些。现在我想来讨论一个特殊问题，这个问题与我密切有关，即如何使这些方程和爱因斯坦的力学理论相一致的问题。我在开头时讲过，只有对运动不太快的，即速度不大，比光速要小得多的粒子，牛顿方程才成立。一当粒子的运动非常快，就必须过渡到一个新的力学，即爱因斯坦的狭义相对论力学。但这个新力学仍然属于牛顿理论的范畴，并且能把它的方程化为哈密顿形式”然而又出现一些特殊的问题，在解决这些问题时，最终要导致反物质的概念。我想来讨论一下这个发展过程的主要特点。

我必须写出一些方程。如果考虑一个粒子的能量，根据牛顿理论，有下面的公式：$$E = \frac {1} { 2 } m v ^ { 2 } = \frac { 1 } { 2 m } p ^ { 2 },$$ 式中 $p$ 是粒子的动量。根据爱因斯坦理论，当 $v$ 很大，即接近光速时，我们必须用 $$E = c \sqrt { m ^ { 2 } c ^ { 2 } + p ^ { 2 } }\tag{6}$$ 来代替上面的公式。看起来爱因斯坦的这个公式与牛顿公式大不相同。首先，差别来自这样的事实：如粒子是静止的，根据牛顿公式，它的能量为零，但根据爱因斯坦公式，它的能量：不为零，而是等于 $mc^2$。

爱因斯坦理论赋予粒子一个额外的能量，这个能量与粒子的速度无关，它叫做静止能量，这种能量被认为禁锢在粒子的内部。当动量 $p$ 的值很小时，爱因斯坦公式是 $$E = m c ^ {2} + \frac { 1 } { 2 m } p ^ { 2 } + \cdots,$$ 后面还有许多包含 $p$ 的高次幂的项，因此在粒子运动不很快的情况下，除额外能量，与牛顿理论相符合¹。

图 1 根据爱因斯坦公式得到的正能级

爱因斯坦能量公式和牛顿公式之间还有另一个差別，即在能量表达式（6）中有一个平方根。从数学上知道，在平方根前面可以取正号或者负号。所以根据爱因斯坦公式，这个能量既可以是正的，也可以是负的。通常人们把能量画成表示各种能级的水平线，根据爱因斯坦公式（6），能级可以是 $mc^2$ 或者是大于 $mc^2$―直到无穷的那些水平线。我们在图 1 中表示了这样一组能级。另外一组能级从 $=mc^2$ 开始一直到负无穷大，大家在图 2 中可比看到。根据爱因斯坦公式，所允许的正负能级如图 3 所示。

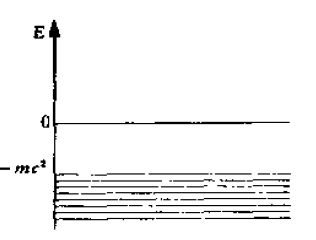图 2 负能级

实际上，人们总是只看到粒子的正能量，所以爱因斯坦公式（6）允许有负能量，而它实际上是观测不到的。开始人们并未担心这件事，只是说：“我们不要管这些负能量，完全用正能量好了。”这样做是允许的，因为如果我们从一个正能态的粒子出发，能量总是保持正值，并且理论中的这些负能量一点也不起作用。

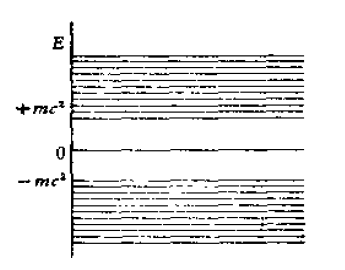图 3 爱因斯坦公式所允许的全部能级

大家知道，在没有外场时，我们可以用公式（6）描述一个粒子。我们也能把这个公式推广到在电磁场中的带电粒子：例如一个电子，而情况并没有多大变化。我们能够在更普遍的条件下计算出能级。我们有洛伦兹方程，即经典方程，这些方程告诉我们，当电磁场作用在粒子上时，根据爱因斯坦力学，粒子将如何运动。

人们用洛伦兹的这些方程来对一个正能量的电子进行计算。人们也可把这些方程应用于一个负能量的电子。据我所知，还没有人作过这种计算。在那时人们对负能量一点也不感兴趣。如果人们从负能态出发，应用洛伦兹方程，对电子如何运动进行计算与考察，就会发现：电子总是保持在负能态上，并且它的运动就好象一个有正能量和正电荷（通常电子带有一个负电荷）的粒子运动一样。这样，对这些负能态，看来好象把电子的能量和电荷都反了一个符号。这就是根据经典力学加上大速度时所需要的爱因斯坦理论修正所得到的结果。

当我们转向量子力学时，情况就不同了。这是因为在量子力学中，动力学变量能从一个值跳到另一个值，并且如果从正能量出发，就不一定保持为正能量，粒子能从一个正能态眺到一个负能态，只要我们硏究的是经典理论，我们就可以根本不管负能态；而在量子理论中，就不能这样做。

虽然这些负能态以一种非常基本的方式出现，但它并未引起人们太多的担忧，因为人们忙于解决更深奥的问题：理解和解释新力学的基本概念；那时这些问题在物理学家中占支配地位。

然而人们仍须正视建立相对论量子力学的问题。如果从德布罗意或薛定谔的波动观点出发来研究量子力学，我们有一个波函数 $\psi$ 并能建立一个相对论波动方程：$$\left(\frac { 1} { c ^ { 2 } } \frac { \partial ^ { 2 } } { \partial _ { t ^ { 2 } } } - \frac { \partial ^ { 2 } } { \partial x _ { 1 } ^ { 2 } } - \frac { \partial ^ { 2 } } { \partial x _ { 2 } ^ { 2 } } - \frac { \partial ^ { 2 } } { \partial x _ { 3 } ^ { 2 } } + \frac { m ^ { 2 } c ^ { 2 } } { k ^ { 2 } } \right) \psi = 0,\tag{7}$$ 根据德布罗意的观点，$\psi$ 所满足的这个方程对应于一个自由粒子。当有电场或磁场存在时，有一个推广的方程可以表明波函数如何随时间变化，这个方程比较复杂，我就不写了，我只想说一下，这个方程是将方程（7）加上一些包含场量的附加项得到的。

现在人们有了单个粒子的波动方程以肚存在电场或磁场时单个电子的波动方程，并且能够对波函数作出相对论的解释”但这个相对论解释与我们对一般的薛定谔理论的解释并不一致，其原因在于方程（7）中有对时间的二阶偏导数 $\frac {\partial ^ { 2} } { \partial t ^ { 2 } }$ 而在一般的薛定谔理论中，则有下面方程：$$i \hbar \frac { \partial \psi } { \partial t } = H \psi,\tag{8}$$ 这个方程对 $\frac { \partial } { \partial t }$ 是线性的。

结果我们发现：根据方程（8）h 由 $[\psi] ^ { 2 }$ 给出的几率总是正的，这正是物理上所需要的。而用方程（7）建立的几率表达式有相対论的形式，但几率并不总是正的。

因此要使量子力学与相对论相一致，存在着真正的困难。那时这个困难使我非常伤脑筋，但它似乎并没有给其他的物理学家带来什么烦恼，其原因我不很清楚。

我想，根据海森堡运动方程（方程 4）和对应的薛定谔方程 （方程 8）建立的表述形式，它的美观及其效能给我非常强烈的印象，以致使我感到人们必须保持这种形式，而过渡到一个以 $\frac {\partial ^ { 2} } { \partial t ^ { 2 } }$ 来代替 $\frac { \partial } { \partial t }$ 的不同类型的方程是不合适的。我特别记得 1927 年在索尔瓦伊会议上的一件事情，在一次演讲的空隙时间，玻尔走到我面前并问我：“你现在在研究什么？”我对他说我正在研究力求找到一个满意的相对论电子理论的问题，当时玻尔回答说，这个问题已经被克莱因解决了 [克莱因得出了方程（7）²］。我试图对玻尔解释，我对克莱因的解决不满意并想向他说明理由。但没能那样做，因为演讲刚好开始，把我们的讨论打断了。但是这件事却使我看清了这样的事实：对于一个理论，其中涉及根本背离量子力学的某些基本定律，而许多物理学家对它十分满意，并且他们并未认识到有坚持这些基本定律的必要性，这和我的看法完全不同。

这个问题使我苦恼了几个月，最后终于得到了解决，我发现了另一个波动方程：$$\left\{i \hbar \left( \frac { \partial} { c \partial t } + \alpha _ { 1 } - \frac { \partial } { \partial x _ { 1 } } + \alpha _ { 2 } \frac { \partial } { \partial x _ { 2 } } + \alpha _ { 3 } \frac { \partial } { \partial x _ { 3 } } \right) + \alpha _ { m } m c \right\} \psi = 0\tag{9}$$ 现在我们得到的是含有 $4$ 个分量的波函数 $\psi$, 而不是象方程（8）中的只有一个分量的波函数 $\psi$，式中 $\alpha_i$ 的是作用在 $4$ 个分量上的矩阵。可以证明：这个方程是一个相对论方程，并且它有一阶偏导数 $\frac { \partial } { \partial t }$，而不是二阶偏导数 $\frac { \partial ^ { 2 } } { \partial _ { t } ^ { 2 } }$，因此这个方 $\frac { \partial } { \partial t }$ 程和量子理论的基本定律相一致。我曾建议把这个方程作为电子的运动方程。

我对这个方程进行了计算，得到电子的自旋为 $\frac {1} { 2 }$ 量子和一个磁矩，这个自旋和磁矩与观测结果相符合。这个结果确实使人大为震惊，因为这意味着：一个粒子的相对论量子理论问题的最简单的解涉及有自旋的粒子。以前我总是认为，最简单的解只涉及无自旋的粒子，而当人们已对无自旋的粒子求出了这个解后，才不得不引进自旋; 而这里却证明最简单的解就包含有自旋。

这个方程很好地解释了理论的许多特点，但是负能问题仍然没有解决。新的理论仍然允许负能量和正能量一齐存在，由于其它问题解决了，所以这个负能困难就成为一个主要问题了。

如果人们利用电子的另一性质，解决负能问题原来是可能的。电子具有这样一种性质，即在同一个态上不能有两个电子。当我们对液函数加上合适的对称性条件时」这个性质就是量子力学定律的一个结果。这个性质是由泡利首先提出来作为解释元素周期表中原子结构的一个方法的。如果在任一态中，不能有一个以上的电子，则在一个原子中就会出现各种电子壳层，一个壳层填满了，再加入的任何电子必须填在外面的壳层中，这样就由一个壳层过渡到另一个壳层，用这个方法，我们建立了化学元索周期表。

如果用量子力学，我们就不能排除从正能态到负能态的跃迁, 这意味着我们不能把负能态从我们的理论中排除出去。既然这样，我们就必须找到一个解释它们的物理学方法。利用一个新的真空概念，人们能够得到一个合理的解释。从前人们把真空看成是一个完全空的空间区域，一个没有任何东西的空间区域。现在我们必须采用一个新的概念。我们可以说，真空是一个具有最低可能能量的空间区域，要得到最低的能量，我们必须填满全部的负能态。填入负能态的电子越多，总能量就越低，因为每增加一个负能态的电子都意味着总能量的减少。因此，我们必须建立新的真空概念，其中所有的负能态都玻电子占据，而所有的正能态都未被占据。

我们能够用两种方法得到非真空态：一个方法是把一个电子填到正能态上；另一个方法是在员能态的分布中产生一个空穴。现在我们着重来看空穴。如果存在一个电磁场，人们就能考查空穴将如何运动的问题。粗略地说，空穴的运动方式和填到那个空穴上的电子的运动方式一样，这和把经过量子修正后的经典洛伦兹方程用于负能粒子得到的结果是一致的。如同我前面所讲的那样，根据经典洛伦兹方程，这个负能粒子的运动就象具有正能量和正电荷的粒子运动一样，因此这些空穴的运动也象具有正能量和正电荷的粒子的运动一样，而不是象通常的带气负电荷的电子运动。空穴表现为具有正电荷的一种新粒子。

这些新粒子的质量是什么？当我首先想到这个问题时，由于对称性使我想到它的质量应当和电子的质量相同，但我未敢贸然地提出这个看法，因为我那时认为，如果这个新粒子（和电子的质量相同，电荷相反）存在，一定已被实验工作者发现，那时大家知道的粒子只有带负电荷的电子和带正电荷的质子，以及其它已经确认有复合结构的原子核。所以我提出了这样的看法：空穴对应于带正电荷的质子。至于为什么空穴的质量和质子的质量会有那么大的差别，我把它作为一个未解决的问题留下来。

当然，这确实是我的很大错误，这正是我缺乏勇气的表现。我本来首先应该说，空穴应和原来的电子具有相同的质量。在我的论文发表之后不久，别人就把它指出来了。我记得韦耳（Weyl）第一个作出非常明确的说明，他说：数学的对称性要求这些空穴应当是具有和电子质量相同的粒子（韦耳是一个数学家，他只对数学的对称性感兴趣，并没有为物理学家从未观测到这种粒子而烦恼)。看来这是一个正确的看法。这些新粒子现在叫做正电子，它们和电子的质量相同而电荷相反。然而又产生这样的问题：“为什么实验工作者从未观测到它们呢？”我认为对这个问题只有一个回答，就是他们那时的成见不赞成新的粒子。

当时认为在自然界中只存在两种基本的粒子：电子和质子。由于只有两种电荷：一种正电荷和一种负电荷，所以只需要两种粒子。只要人们对负电荷有一种粒子，对正电荷也有一种粒子就足够了。我们不需要任何别的粒于，这就是当时普遍流行的思想。

实验工作者所以从来没有观测到正电子，是因为他们对自己得到的证据视若无睹。大家知道，人们能用威尔逊云雾室观测带电粒子的径迹，如果还存在一个磁场, 径迹就会发生弯曲。现在如果有一个带正电的粒子沿着某个方向运动，这就好象一个带负电的粒子沿着相反的方向运动一样，两者的径迹应当是相同的。人们可以认为所观测到的全部径迹都是电子的，都对应于带负电的电子，而且全都沿着按负电荷应有的方向运动。然而有些实验工作者已经注意到：当有一个放射源时，他们常常观测到粒子向源运动。事实上，根据上述解释，甚至还发表过一两张粒子向源运动的径迹照片，但从没有人费力去作统计。如果他们真的作了统计，就会注意到向源运动的粒子数目是很多的，以致不可能作这种解释。在那些日子里，情况就是这样，人们非常不愿意提出一个新粒子。

现在情况就完全不同了。不论在理论上或实验上，人们凭很少的证据就提出新粒子。那时为了确定正电子却需要花几年的时间。关于正电子的存在问题，布莱凯特（Blackett）提出过一些相当令人信服的证据，并且在剑桥他把这件事告诉了我，可是他对发表这样一个革命性的发现非常犹疑不决，他希望再证实他的实验，由于这一延误，这个发现被安德森抢先发表了。当时安德森仅有这样一张穿过一块铅板的径迹照片（如图 4 所示）。从图上可看出径迹在板的一边比另一边弯曲得厉害，既然粒子在穿过铅板时，必定要损失能量，而不可能获得能量，因此这就非常清楚地确定了粒子的运动方向，而这个方向正好对应于具有正电荷的粒子。

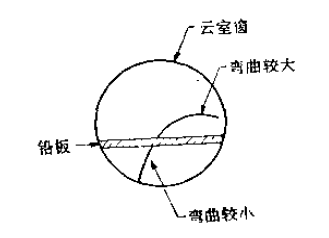图 4 安德森观测正电子在云室内穿过铅板的实验示意图

这个发现证明了电子具有和它对应的反粒子，即正电子的存在。反粒子的概念在原子理论中实际上是十分普遍的概念。对于在任一态中不能有多于一个粒子的那些粒子〔叫做费米子除正能态之外，还有负能态。在真空中，所有负能态全被占满, 而在实际中则差不多全部被占满。负能态中任意一个空穴对应于一个反粒子，现在把这个概念用于质子，就有反质子；把它用于中子，就有反中子。现在人们已经观测到这些粒子。

有了反物质的概念，我们就必须改变我们对基本粒子（或叫基础粒子）的看法。这些粒子能从一些其它形式的能量中产生出来，例如从电磁波的能量中产生出来。我们可以用电磁波扰动真空，把一个负能电子拉到正能态上，这样就产生出一个电子和一个正电子。电子和正电子是同时产生的。当然，电荷是守恒的，能量必须从外源得到。对其它费米子也有类似的情况。

如果我们能够产生出粒子，则什么是物质的基本成分的问題冠再有明确的意义。以前人们可以说尽可能地把物质分解为小块，就能得到物质的最终组成部分。但如果人们能用原子的相互作用来产生粒子，就不能对基本粒子下一个确切的定义了。随着现代物理学的发展，发现了大量的粒子，不仅仅是两种粒子——电子和质子，现在我们发现的粒于已经有二百多种，它们当中许多都是很不稳定的，其中一些极不稳定，另一些比较不稳定，如果人们问这些新粒子中哪些是基本粒子，对这个问题确实不能作出明确的回答。也许倾向于认为比较稳定的粒子是基本粒子，比较不稳定的粒子不是基本粒子，但这多少是人为地划分。例如质子和中子，它们在许多方面是非常相似的，但质子是稳定的，而中子是不稳定的。若把它们中的一个看成是基本粒子，另一个不是基本粒子就不合理。因此哪些粒子是基本粒子是一个尚未解决的问题，这也是物理学家当前所关心的问题。

上面我已经讲了量子力学发展的问题、并且特别讨论了这个理论与高速运动所必须的爱因斯坦力学相结合的问题，这个结合导致产生反物质的概念。然而这个工作并没有解决量子理论的问题，还有许多遗留的问题，这些遗留的问题集中在建立带电粒子和电磁场相互作用的精确理论的问题上。

你们可以把带电粒子的电荷看成集中在一个点上，对这个点模型进行研究。如果你用这样的模型，那就会发现点电荷的能建是无穷大的。这是试图建立粒于相互作用精确理论时出现的典型困难。

假如我门不把量子理论推广得太远，即不把它用于能量非常高的粒子，也不把它用于非常小的距离，那么现在的量子理论是很好的。当我们试图把它推广到高能粒子和很小距离时，我们得到的方程就没有合理的解, 相互作用总是导致无穷大的出现，这个问题使物理学家困惑了 40 年，没有取得任何实质性的进展。

正是由于这些困难，我认为量子力学的基础还没有正确地建立起来。在当前这个基础上所进行的研究，在应用方面已经做了极其大量的工作，在这方面，人们能够找出抛弃无穷大的一些规则。然而即使板据这些规则得出的结果与观测相符合，但毕竟是人为的规则。因此关于现在的量子力学基础是正确的说法，我是不能接受的。

我觉得当前关于这些无穷大的情况和人们研究有 $\frac {\partial ^ { 2} } { \partial t ^ { 2 } }$ 波动方程时的情况非常相似。我认为人们太乐于接受一个有基本缺陷的理论了。只有在对这些理论作出象从方程（7）过渡到方程（9）那样的根本改变时，才能取得真正的进展。

注释：
1. 牛顿力学只考虑
$E = m c ^ { 2 } + \frac { 1 } { 2 m }p ^ { 2 }+ \dots$
中的第二项$\frac { 1 } { 2 m }p ^ { 2 }$——译者注
2. 方程(7) 称为克莱因——高登方程——译者注