是否 $\sqrt{2 }-1$ 的所有正整数幂都可以表示为两个相邻正整数的平方根之差？

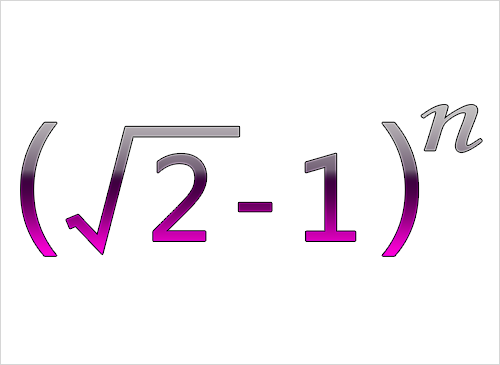
参考答案

步骤一

可以分两组情况来讨论$(\sqrt 2 -1)^n.$

(1) n 是偶数

$n=2$ 时显然满足.

假设 $n=2k$ 时， $(\sqrt 2 -1)^{2k}-A-B\sqrt 2-\sqrt{A^2}-\sqrt{2B^2}$, 其中 $A^2-2B^2=1.$

则 $(\sqrt 2 -1)^{2k+2}=(\sqrt 2 -1)^2(\sqrt 2 -1)^{2k}$

$=(3-2\sqrt 2)(A-B\sqrt 2)=(3A+4B)-\sqrt 2(2A+3B)$

$=\sqrt{(3A+4B)^2}-\sqrt{2(2A+3B)^2}$

易得 $(3A+4B)^2- 2(2A+3B)^2=A^2-2B^2=1$

步骤二

n是奇数.

$n=1$ 时显然满足.

假设 $n=2k-1$ 时， $(\sqrt 2 -1)^{2k-1}=C\sqrt 2-D=\sqrt{2C^2}-\sqrt{D^2}$, 其中 $2C^2-D^2=1.$

则 $(\sqrt 2 -1)^{2k+1}=(\sqrt 2 -1)^2(\sqrt 2 -1)^{2k-1}$

$=(3-2\sqrt 2)(C\sqrt 2-D)=\sqrt 2(3C+2D)-(4C+3D)$

$=\sqrt{2(3C+2D)^2}-\sqrt{(4C+3D)^2}$

易得 $2(3C+2D)^2- (4C+3D)^2=2C^2-D^2=1$

综上所述, $(\sqrt {2 }-1)$ 的所有正整数幂都可以表示为两个相邻正整数的平方根之差.

网友帅小呆提供两种解法

$(\sqrt {2 }-1)$ 的所有正整数幂都可以表示为两个相邻正整数的平方根之差.

证明：

$(\sqrt 2-1)\cdot(\sqrt 2+1)=1 \Rightarrow (\sqrt 2-1)^n\cdot(\sqrt 2+1)^n=1$

$(\sqrt 2-1)^n=\sqrt(a+1)-\sqrt a~(a\in N) \Leftrightarrow (\sqrt 2+1)^n=\sqrt{a+1}+\sqrt a$.

所以原命题等价于“$(\sqrt 2+1)^n$ 可以表示为两个相邻正整数的平方根之差.”

由二项式展开，不妨设 $(\sqrt 2+1)^n=x+y\sqrt 2~~(\exists x,y\in N)$,

则 $(\sqrt 2+1)^n=\sqrt{x^2}+\sqrt{2y^2}$, 数学归纳法证明 $\forall N\in N,~\exists x,y\in N:~|x^2-2y^2|=1$

$n=1,(\sqrt 2+1)^n=\sqrt 2+1=\sqrt{1^2}+\sqrt{2\times 1^2},~x=y=1,~|x^2-2y^2|=1$ 成立；

$n=2,(\sqrt 2+1)^2=2\sqrt{2}+3=\sqrt{3^2}+\sqrt{2\times 2^2},~x=3,~y=2,~|x^2-2y^2|=1$ 成立；

假设： $n=k,~\forall x_k,y_k\in N:~|x_k^2-2y_k^2|=1,~(\sqrt 2+1)^k=x_k+y_k\sqrt 2$

则 $(\sqrt 2+1)^{k+1}=(x_k+y_k\sqrt 2)\cdot(1+\sqrt 2)=(x_k+2y_k)+(x_k+y_k)\cdot \sqrt 2$

$x_{k+1}=(x_k+2y_k),~~y_{k+1}=(x_k+y_k),$ 则 $(\sqrt 2+1)^{k+1}=\sqrt{x_{k+1}^2}+\sqrt{2y_{k+1}^2}$ 且有

$|x_{k+1}^2-2y_{k+1}^2|=|(x_k+2y_k)^2-2(x_k+y_k)^2|=|-x_k^2+2y_k^2|=|x_k^2-2y_k^2|=1$

所以 $(\sqrt 2+1)^n$ 总可以表示为两个相邻正整数的平方根之差.

$(\sqrt {2 }-1)$ 的所有正整数幂都可以表示为两个相邻正整数的平方根之差.

$(\sqrt 2-1)^n$ 总可以表示为两个相邻正整数的平方根之差.

证明：(不用数学归纳法)

令 $a=\dfrac{(\sqrt 2+1)^n+(\sqrt 2-1)^n}{2}>0,~~b=\dfrac{(\sqrt 2+1)^n-(\sqrt 2-1)^n}{2}>0$

则 $a-b=$(\sqrt 2-1)^n=\sqrt{a^2}-\sqrt{b^2}$ 且 $a^2-b^2=1$

只需证明n为奇数或偶数时 $a^2$ 和 $b^2$ 都为正整数即可.

由二项式展开，$\forall x,y\in Z^+$ 使 $(\sqrt 2+1)^n=x+y\sqrt 2$, 则：

n为奇数时， $(\sqrt 2-1)^n=y\sqrt 2-x~\Rightarrow~a^2=2y^2,~b^2=x^2\in Z^+$

n为偶数时， $(\sqrt 2-1)^n=x-y\sqrt 2~\Rightarrow~a^2=x^2,~b^2=2y^2\in Z^+$

所以 $(\sqrt 2-1)^n$ 总可以表示为两个相邻正整数的平方根之差

是否还可以这样做呢？

证明：

根据二项式定理，设 $(1-\sqrt 2)^n=m-n\sqrt 2$, 则

$(\sqrt 2+1)^n=M+N\sqrt 2$, 其中 $M,N \in R^+$.

$(-1)^n=(1-\sqrt 2)^n(1+\sqrt 2)^n=(M-N\sqrt 2)(M+N\sqrt 2)=M^2-2N^2$, 所以

$(1-\sqrt 2)^n=M-N\sqrt 2=\sqrt{M^2}-\sqrt{2N^2},$ 且 $|M^2-2N^2|=1$.

我认为这是一道好题，可在二项式定理的教学中使用。在解题当中，时时冲击我脑子的是一个词：数域。形如 $a+b\sqrt 2$ （其中a和b是有理数）所组成的集合是一个数域！也就是任取 $a_1+b_1\sqrt 2$ 和 $a_2+b_2\sqrt 2$ ，经过加减乘除运算还是形如 $a+b\sqrt 2$ 。而二项式定理不过是多次乘法罢了！

汤涛教授（《数学文化》杂志的主编）对此题评论如下：
数学文化： 什么叫好题目？1：简单易记、容易转述；2：有一定的数学；3：看起来漂亮。这道题属于好题；大家学会了，以后很多场合都可以解解闷，或被窝里伸脚丫——露一小手。