Rainbow Zyop

I

...Von viel größerem Interesse sind aber Arbeiten EULERS, welche im Msc. eine ganz andere Gestalt haben, als welche er ihnen später gegeben hat, so daß man sieht, daß er keineswegs so wie man glauben möchte die Publication seiner Arbeiten übereilt hat, sondern sie bisweilen lange liegen ließ und mehrfach umarbeitete. ...Bei dieser Gelegenheit habe ich auch einen für die Geschichte der Mathematik ungemein wichtigen Tag gefunden, an welchem unsere Akademie Euler auffordert das von Fagnani ihr übersandte Werk zu prüfen, ehe man dem Verfasser antwortet. Aus dieser Prüfung ist die Theorie der elliptischen Functionen entstanden.

……然而更富有趣味的是Euler在Msc.[当指Miscellanea Berolinensia，柏林科学院刊行的杂志]上发表的工作，这些工作和他后来[在同一主题上]发表的工作形式上是截然不同的，因此可以看到，他的工作并不是如人们所想，是一蹴而就的，而是有时会搁置很长一段时间，而且会在[一个问题上]工作好几次。……借此机会我也找出了数学史上非常重要的一天——这一天我们科学院[指柏林科学院]邀请Euler来审阅Fagnano的工作，以便给作者作出回复。椭圆函数论就诞生于这次审阅之中。

[上述文字引用自C. G. J. Jacobi 1847年10月24日致Paul Heinrich Fuss的信。P. H. Fuss是Nicholas Fuss之子。Nicholas Fuss曾经师从Euler, 并且娶Euler的孙女为妻。Jacobi与Fuss都对Euler的数学工作进行过详尽的整理。题图所示正是Jacobi发给Fuss的Euler学术活动清单的一部分，这份清单中明确写道：Euler受邀审阅Fagnano的工作始于1751年12月23日。]

---

Giulio Carlo, Conte Fagnano e Marchese de' Toschi e di Sant'Onofrio(1682-1766), 1682年9月26日生于意大利亚得里亚海畔的Sinigaglia。Fagnano本人出身于当地的名门望族，爱好数学，哲学与诗歌。1743年他参与了圣彼得大教堂的修缮工作，作为奖励，教皇本笃十四世准许刊行他的数学论文集。不过他的全集直到1750年才完成印刷。1745年教皇封他为侯爵。他的一个儿子Giovanni Fagnano也是数学家，但是他的成就比不上他的父亲。根据记载，Fagnano家已经绝嗣。

“古者富贵而名摩灭，不可胜记”，Fagnano的工作也不得不接受这样的命运。1933年G. N. Watson在他的文章“The Marquis and the Land-agent,...”中明确写道：

...his investigations on the geometrical theory of proportion, which occupy a large part of the first volume of his Produzioni matematiche, are, of course, irrelevant, and I do not hesitate to say that I naturally consider them rather dull reading.

他的数学文集(总计1000多页)到今天也就只有只有一项工作能够流传于世，而这项工作就印在文集的扉页上。(下图摘自Google Book Fagnano文集的第二卷)

他对自己的这项工作的重视也可以从他传世的画像中看到。

---

Fagnano研究的主要是曲线求长问题。如他论文集中说的，他的研究主要受到Bernoulli兄弟的启发[意大利语原文来自Fagnano文集第二卷, p. 343, 译文由Patrick Popescu-Pampu的书“What is the genus?”中的英译文给出]：

Due sommi geometri sig. Giacomo, e sig. Giovani fratelli Bernulli anno renduta celebre la lemniscata, servendosi de' suoi archi per costruire l'isochrona paracentrica, come può vedersi negli atti di Lipsia dell' anno 1694. Egli è visibile, che misurando la lemniscata mediante qualche altra curva di lei più semplice, si ottiene una costruzione più perfetta non solo dell' isochrona paracentrica, ma ancora delle altre infinite curve, che per essere costruite possono dipendere dalla lemniscata ; e però mi lusingo, che non sieno per dispiacere agl'intendenti le misure di questa curva da me scoperte, le quali esporrò successivamente in due schediasmi.

两位伟大的数学家，Jacob Bernoulli与Johann Bernoulli因为借助双纽线的弧长构造出等时曲线而使双纽线闻名于世，这可以从1694年莱比锡的[杂志]Acta [Eruditorum]中看到。可以看到，如果用某些更简单的曲线来度量双纽线[的弧长]，我们不仅可以得到等时曲线[注：这个不是Huygens等人研究的等时曲线]更漂亮的构造，而且可以依赖双纽线构造出无穷多条其他的曲线。这条曲线[弧长的]度量由我发现，并且发表在[这]两篇短文中，这项工作会使理解这个主题的人感到愉悦，我会为此感到自豪。

Bernoulli等人研究的问题是与两个物理问题有直接关联的。[下图来自1691年的Acta Eruditorum的插页, p. 282]

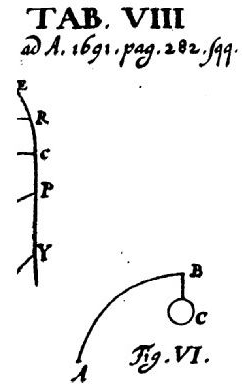
问题1：有一根均匀弹性轻质杆AB，杆自身重量忽略不计。固定杆的一端A，使之处在竖直状态。在杆的另一端B悬挂一个重物，试确定弹性轻质杆AB的形状。[其实也应当假设杆的形状是平面曲线]

1691年Jacob Bernoulli在公布此问题时放了一条谜语进去：

Qrzumu bapt dxqopddbbp poyl fy bbqnfqbfp lty ge mutds udtbh tubs tmixy yxdksdbxp gqsrkfgudl bg ipqandtt tcpgkbp aqdbkzs.

这是解决问题的关键。三年后他才公布答案：

Portio axis applicatam inter et tangentem est ad ipsam tangentem sicut quadratum applicatae ad constans quoddam spatium.

按这里的说法，解密后的内容即便翻译成英文也很难懂。只有深入他1694年的著作以后，我们才会明白，这一句指的是：[在理想情况下(杆的形变遵循胡克定律)，]外力对弹性杆上任意一点的力矩与杆在该点的曲率成正比[Jacob Bernoulli自己称之为theorema aureum(黄金定理)]。Daniel Bernoulli与Euler后来进一步把弹性杆与梁的理论发扬光大[例如用变分法]，这里我们略去不提。

据此，我们立刻可以写出杆形状的微分方程：

$$\frac{\mathrm{d}}{\mathrm{d}x}\frac{f^{\prime}}{\sqrt{1+(f^{\prime})^2}}=2cx$$

常数c与杆的弹性系数[如杨氏模量]以及外力有关。它有一个特解满足

$$\frac{f^{\prime}}{\sqrt{1+(f^{\prime})^2}}=cx^2$$

此时杆的顶端是水平的。我们于是得到

$$f^{\prime}=\frac{cx^2}{\sqrt{1-(cx^2)^2}}\Longrightarrow f(u)=\int_{0}^{u}\frac{cx^2}{\sqrt{1-(cx^2)^2}}\mathrm{d}x$$

这就是Jacob Bernoulli给出的弹性曲线的解。

---

1694年Jacob Bernoulli在发表了弹性曲线的工作之后，又解决了Leibniz 1689年提出的另一个问题：

问题2：一质点在重力作用下在竖直平面内沿着某条曲线C运动。设曲线上一点为O。记曲线上AB两点间的直线距离为 $\overline{AB}$ ,从A到B运动的时间为 $t(AB)$ . 如质点趋近/离开O点时，t(AO)(或t(OA))总与OA两点间直线距离成正比，试求曲线C的方程。

很显然解决问题的关键在于建立合适的微分方程。考虑在极坐标 $x=\rho\cos\theta,y=\rho\sin\theta$ 下研究此问题，并取O点为原点。根据能量守恒，我们立刻有 $\frac{1}{2}mv^2=E_0+mgy$ ,约束条件为 :$\frac{\mathrm{d}\rho}{\mathrm{d}t}$ 是常数。在极坐标下我们有 $v^2=\left(\rho\frac{\mathrm{d}\theta}{\mathrm{d}t}\right)^2+\left(\frac{\mathrm{d}\rho}{\mathrm{d}t}\right)^2$ 。如果在O点处 $\frac{\mathrm{d}\theta}{\mathrm{d}t}$ 有限，我们就可以得到 $\frac{1}{2}m\left(\frac{\mathrm{d}\rho}{\mathrm{d}t}\right)^2=E_0$ 。此时我们的方程就可以化为 $\frac{1}{\sqrt{\rho}}\mathrm{d\rho}=K\frac{1}{\sqrt{\sin\theta}}\mathrm{d}\theta$ 。我们再令 $\sin\theta=z, u=\sqrt{z}$ ,也就有

$\frac{1}{\sqrt{\rho}}\mathrm{d\rho}=K\frac{1}{\sqrt{z-z^3}}\mathrm{d}z$ 以及

$\frac{1}{\sqrt{\rho}}\mathrm{d\rho}=K^{\prime}\frac{1}{\sqrt{1-u^4}}\mathrm{d}u$ (K与K'均为常数)。

这条曲线和弹性曲线有什么关系呢？十七-十八世纪的数学家涉及到单变量积分的时候，通常倾向于把积分描述为曲线围绕的面积或曲线的弧长。从弹性曲线的表达式我们可以推导出它的弧长微分 $\mathrm{d}s=\sqrt{(\mathrm{d}f)^2+(\mathrm{d}x)^2}=\frac{1}{\sqrt{1-(cx^2)^2}}\mathrm{d}x$ , 与我们上面得到的微分方程的右侧相比只有一些常数因子上的差别，因此Leibniz的曲线就可以用弹性曲线的弧长来描述。

Jacob Bernoulli是不满足于这样的结果的。弹性曲线并不是代数曲线。上面的弧长微分有没有可能是某条代数曲线的弧长微分呢？我们来看一下Jacob的弟弟Johann Bernoulli在同年给出的答案：

注意到我们上面在推导Leibniz曲线的过程中微分方程右边出现了 $\frac{1}{\sqrt{z-z^3}}\mathrm{d}z$ 这样一项。如果它是代数曲线的弧长微分，那么 $\frac{1}{z-z^3}(\mathrm{d}z)^2=(\mathrm{d}u)^2+(\mathrm{d}v)^2$ 。Johann Bernoulli把左边裂成两项： $\frac{1}{z-z^3}(\mathrm{d}z)^2=\frac{1}{2}\frac{1+4z+4z^2}{z+z^2}(\mathrm{d}z)^2+\frac{1}{2}\frac{1-4z+4z^2}{z-z^2}(\mathrm{d}z)^2$

Johann Bernoulli注意到，两项分别是 $\mathrm{d}\sqrt{2z+2z^2}$ 和 $\mathrm{d}\sqrt{2z-2z^2}$ 的平方。因此我们就找到了待定曲线的参数方程： $u=\sqrt{2z+2z^2},v=\sqrt{2z-2z^2}.$ 参数方程确定的曲线的形状是这样的：

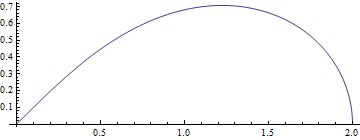
这正是双纽线的1/4。

可叹的是在Leibniz曲线上的工作成了Bernoulli兄弟二人反目的导火索。Johann在发表自己的研究后，Jacob却对Johann的研究大加指责，认为Johann的研究毫无意义。Johann Bernoulli在1695年1月12日写给Guillaume de l'Hôpital的信中这样写道[原文来自Der Briefwechsel von Johann I Bernoulli，1955，p. 253-257，译文来自Jeanne Peiffer的英译Peifferanglais3]：

...c'est un misantrope general qui n'epargne pas méme son frere, comme vous voyez par tout ce qu'il m'a fait, il créve de rage, de haine, d'envie et de jalousie contre moy, ...enfin ce seroit avec le plus grand plaisir de me voir dans l'état le plus miserable et reduit à l'extremité...cependant n'ayez pas peur, que je fasse part à mon frere de ce que nous nous ecrivons, car il y a plus de 6 mois que je ne luy ay parlé mot.

……他厌世到连自己的兄弟都不宽恕，你也看到了，他心中充满了对我的愤恨嫉妒之情,……简单说，能看到我陷入悲惨的境地中一路落到底那是最能令他满足的事情..……不过你不用怕，我会把我们之间通信的内容告诉他，因为我已经六个月没和他说过一句话了。

这两人的关系直到1705年Jacob Bernoulli去世都没能缓和过来。正是所谓的“一尺布，尚可缝，一斗粟，尚可舂。……”

问题：有人看出来Jacob Bernoulli是怎么加密自己的信息的吗？

II

Un Géomètre italien, d'une grande sagacité, ouvrit la route à des spéculations plus profondes. Il prouva que sur toute ellipse ou sur toute hyperbole donnée, on peut assigner, d'une infinité de manières, deux arcs dont la différence soit égale à une quantité algébrique. Il démontra en même temps que la lemniscate jouit de cette singulière propriété, que ses arcs peuvent être multipliés ou divisés algébriquement, comme les arcs de cercle, quoique chacun d'eux soit une transcendante d'un ordre supérieur.

一位极其敏锐的意大利数学家开辟了一条[通往]更深刻思考的道路。他证明了：任意给定椭圆或双曲线，我们有无穷多种不同的方式指定[曲线上的]两条弧，使得弧长的差值可以[仅由]代数量表示。同时他也证明了双纽线的非同寻常的性质，也就是双纽线弧长[加倍或平分]可以[仅]通过代数运算表示，这与圆弧的性质是相同的，尽管双纽线的弧长[相比圆弧而言]是更高阶的超越函数。

[上文摘自Legendre1811年的书Exercices de calcul intégral...第1-2页; 题图是Fagnano 1718年关于双纽线弧长倍乘公式的文章的照片。本文与Fagnano有关的最重要的材料来自La lemniscate de Fagnano et la multiplication complexe和Raymond Ayoub的文章“The Lemniscate and Fagnano's Contributions to Elliptic Integrals”，1984]

1698年Johann Bernoulli 在Acta Eruditorum发表了一篇关于题名为Theorema universale rectificationi linearum curvarum inserviens...[用于曲线求长的一个普适定理...]的文章。我们今天知道，绝大多数曲线的弧长不能用初等函数表示，Johann Bernoulli应当也察觉到了这一点。虽然这些曲线的弧长不能用初等函数表示，但是Johann Bernoulli提到：弧长的和或差有可能可以用初等函数表示。

例子：立方抛物线 $ y=x^3/3 $ 的弧长可以用积分 $ \int\sqrt{1+x^4}\mathrm{d}x $ 表示。我们今天知道，这个积分不能用初等函数表示。但是，这条曲线上某两段弧长的差却可以用初等函数表示。利用分部积分，我们很容易得到

$$ \int\sqrt{1+x^m}\mathrm{d}x=\frac{2}{m+2}x\sqrt{1+x^m}+\frac{m}{m+2}\int\frac{1\,}{\sqrt{1+x^m}}\mathrm{d}x $$

注意到如果对最后一个积分号内的变量换元： $ x=1/u, $ 那么积分号内的微分形式只有符号发生变化。所以我们可以确定：弧长 $ \int_{u_1}^{u_2}\sqrt{1+x^4}\mathrm{d}x $ 以及弧长 $ \int_{1/u_2}^{1/u_1}\sqrt{1+x^4}\mathrm{d}x $ 的差值可以用 $ u_1,u_2 $ 的初等函数表示。

---

Fagnano在Johann Bernoulli的基础上提出了下面的问题[此问题最早发表在意大利的杂志Giornale de' letterati d'Italia，Vol. XIX，1714，后来编入Fagnano文集第二卷315-316页,译文来自 D. J. Struik的书A Source Book of Mathematics, 1200-1800，第375页]:

Problema: Sia data una parabola biquadratica primaria, che à per equazione costitutiva $ x^4=y $ , e sia data ancora una porzione di essa; dimando, che si assegni un' altra porzione nella medesima curva tale, che la differenza delle porzioni suddette sia rettificabile.

问题：给定四次抛物线，其方程由 $ x^4=y $ 给定，并指定曲线上的某一段[弧]。试问如何找到曲线上另一段弧，使得两段弧长的差值可以求长[注：此处的求长指的是弧长差值可以用弧始末点坐标的初等函数表示]

这表明，Fagnano思考的问题已经从上面m=4的情形移到更一般的m所对应的情形。1715年Fagnano在同一杂志上发表了自己对这一类问题的解法。

按照上面的叙述，如果我们能找到代数函数 $ x=\phi(u) $ 使得

$ \frac{1\,}{\sqrt{1+x^m}}\mathrm{d}x+\frac{1\,}{\sqrt{1+u^m}}\mathrm{d}u=0 $ 成立，那么Bernoulli关于立方抛物线的结论立刻就可以推广到更广泛的一类曲线上面去。问题就在于：怎么去猜测代数函数 $ \phi $ 的形式。

1715年Fagnano在这篇题名为Nuovo Metodo...的文章中给出了如下定理：

定理：若 $ (x^n+p)(z^n+p)=r $ , 那么
$ \frac{x^{n-1}(x^n+p)^{h-1}\,\mathrm{d}x}{E^h}=-\frac{z^{n-1}(z^n+p)^{h-1}\,\mathrm{d}z}{E^h} $ ,其中
$ E=(x^n+p)^2+q(x^n+p)+r $ ,p,q,r,h,n是任意常数。

我们如果令 $ P=x^n+p,Q=z^n+p $ ,那么定理的证明是平凡的。尽管定理的证明是平凡的，我们却不知道Fagnano提出这个定理的动机是什么。也许Fagnano完全是靠配凑得到上面这个定理。

Fagnano的定理中有5个自由常数。通过指定不同的常数，我们就有希望推广Bernoulli的结论。令h=1/2, p=n=1,q=-3,r=3或h=1/2, p=n=2,q=-3,r=3我们就可以得到上面m=3或6的解。如果我们取h=1/2,n=1,p=1, r=2, q=-3，那么我们可以得到：

如果 $ (x+1)(z+1)=2 $ ，那么 $ \frac{1\,}{\sqrt{x-x^3}}\mathrm{d}x=-\frac{1\,}{\sqrt{z-z^3}}\mathrm{d}z $ 。

左侧的微分形式正是上一篇中由Bernoulli兄弟推导出的双纽线的弧长微分。如果x=z,借助已经得到的结论以及上篇中双纽线的参数方程，我们容易推出， $ x=\sqrt{2}-1 $ 对应的点刚好将双纽线在第一象限的部分分成弧长相等的两段。

---

1717年7月23日Fagnano在写给G[uido] Grandi的信中这样写道[原文来自Fagnano文集第三卷，翻译为DeepL无责任翻译]：

...Nello stesso Giornale 29 si trova uno de' miei schediasmi sopra la maniera di misurare la Lemniscata, che i due Sig. fratelli Bernulli Giacomo e Giovanni, non hanno saputo trovare con dagli Atti di Lipsia può riconoscersi.

在Giornale[de' letterati d'Italia]杂志第29卷上有我关于双纽线弧长的文章，这篇文章的内容尚未出现在Bernoulli兄弟在Acta Eruditorum上所发表的文章当中。

Fagnano所指的文章题名为Metodo per misurare la lemniscata[双纽线(弧长)的度量方法],分两篇发表在1718年刊行的Giornale de' letterati d'Italia杂志29卷和30卷上。我们把上面得到的结论改头换面一下，就可以得到第一篇文章的一个重点结论：

如果 $ x^2=\frac{1-z^2}{1+z^2} $ , 那么我们就有 $ \frac{1\,}{\sqrt{1-x^4}}\mathrm{d}x=-\frac{1\,}{\sqrt{1-z^4}}\mathrm{d}z $ 。

Raymond Ayoub在1984年的一篇文章“The Lemniscate and Fagnano's Contributions to Elliptic Integrals”中作出了如下猜测(仅仅是猜测，Fagnano本人的动机已经无从见到，他本人的文章中只有证明而没有动机的阐述，相比之下Euler真正是数学家中的异类)：

$ x^2=\frac{1-z^2}{1+z^2} $ 右侧正是万能公式中余弦函数的形式。在验证自己结果的时候，Fagnano可能尝试将右侧换为正弦函数的形式，也就是 $ x^2=\frac{2z}{1+z^2} $ ,并且计算 $ \frac{1\,}{\sqrt{1-x^4}}\mathrm{d}x $ 的值。

如果 $ x^2=\frac{2z}{1+z^2} $ ，等式两边微分，我们就有 $ x\,\mathrm{d}x=\frac{1-z^2}{(1+z^2)^2}\,\mathrm{d}z $ 。而 $ \sqrt{1-x^4}=\frac{1-z^2}{1+z^2} $ ,因此我们可以断言，此时 $ \frac{1\,}{\sqrt{1-x^4}}\mathrm{d}x=\frac{1}{x(1+z^2)}\mathrm{d}z=\sqrt{\frac{1}{2z(z^2+1)}}\mathrm{d}z $ 。

所以如果 $ x^2=\frac{2z^2}{1+z^4} $ ,那么我们就有 $ \frac{1\,}{\sqrt{1-x^4}}\mathrm{d}x=\sqrt{\frac{2}{1+z^4}}\mathrm{d}z $ 。这样我们就得到了Fagnano 1718年第二篇文章的第一个定理(如题图所示)。以稍微现代一点的观点来看，如果我们用 $e^{\pi i/4}x$ 代替 $ x $ ，用 $e^{\pi i/4}z$ 代替 $ z $ ，我们立刻可以得到Fagnano 1718年第二篇文章的第三个定理：

如果 $ x^2=\frac{2z^2}{1-z^4} $ ，那么 $ \frac{1\,}{\sqrt{1+x^4}}\mathrm{d}x=\sqrt{\frac{2}{1-z^4}}\mathrm{d}z $ 。

[我们当然也可以猜测，Fagnano尝试了所有可能的万能公式。上边的式子对应的正是正切的万能公式。]

作一次复合，我们就得到

如果 $ x^2=\frac{4z^2(1-z^4)}{(1+z^4)^2} $ ，那么 $ \frac{1\,}{\sqrt{1-x^4}}\mathrm{d}x=\frac{2}{\sqrt{1-z^4}}\mathrm{d}z $ 。这就是双纽线弧长的倍乘公式。

Fagnano借助自己两篇文章的结论，成功地找到了双纽线弧长的三等分点和五等分点。他同时断言，(第一象限的)双纽线可以进行 $2^m,3\times 2^m,5\times 2^m$ 等分(等分点是尺规可作的)。他应当对自己的结果感到十分自豪，在1718年第二篇文章的末尾写道：

E questa è una nuova, e singolare proprietà della mia curva.
这是我的曲线一个崭新而奇特的性质。

Fagnano有理由为自己的结果而自豪，不过，这条曲线真正的“singolare proprietà”还有赖于Fagnano的审稿人来发掘。

III

Euler, par une combinaison qu'on peut regarder comme fort heureuse, quoique ces hasards n'arrivent jamais qu'à ceux qui savent les faire naître , trouva l'intégrale algébrique complète d'une équation différentielle composée de deux termes séparés, mais semblables, dont chacun n'est intégrable que par des arcs de sections coniques.

Euler, 在一次可以说是非常幸运的[代数式的？]组合中——尽管说这样的幸运仅仅降临在给它们以生命的人的身上——找到了[某个]微分方程的代数解，这个微分方程两侧不含相同的变量，而且对方程两侧的任意一侧积分都只产生圆锥曲线的弧长。

[上文摘自Legendre1811年的书Exercices de calcul intégral...第2页，题图是Euler 1752年宣读，1761年发表的论文Observationes de comparatione arcuum curvarum irrectificibilium中关于双纽线的插图]

Morris Kline在其《古今数学思想》一书中这样写道[第18章第4节]：

Count Giulio Carlo de' Toschi di Fagnano (1682-1766), an amateur mathematician, began in 1714 to take up these problems.

但当时欧洲的数学界肯定不觉得Fagnano是业余数学家。1750年，Fagnano被提名为柏林科学院成员。1754年，时年十八岁的Lagrange也曾写信给Fagnano寻求学术上的指点。Fagnano此时已经是七十多岁的老人，在来往信件中除了一些客套话以外并不能给Lagrange以真正的指点。Lagrange在同年也曾经寻求另一位大人物的帮助，但没能得到及时的回应。次年他与这位大人物终于取得了联系，这位大人物正是本篇的主人公——Euler。

开篇引用Jacobi的信件中提到了Fagnano与Euler之间的关系。Fagnano被提名柏林科学院成员并不意味着他就能当选。柏林科学院需要找一位合适的数学家来评价Fagnano在数学方面的成果。根据柏林科学院的记录[记录用法语写成]，1751年12月23日，Fagnano的著作来到了Euler的案头。Weil的数论史记载(p. 245), Euler本人

On reading those few pages Euler caught fire instantly;...

因为他在次年1月27日就向柏林科学院宣读了一篇长度大约30页的论文[Euler在2月1日与Pierre Louis Maupertuis的通信中曾经提到这篇文章中的一个结论]，而在4个月之后(5月30日)与Goldbach的通信中已经提到了1753年4月30日另一篇相关文章中的部分重点内容，考虑到Euler在同一时间还在处理其他完全不同的数学问题，这种速度可以说是神速了。后人曾经整理Euler在这个主题上的工作，统计结果证明，Euler大概就这个主题写了二三十篇文章。

Euler 1752年在柏林科学院宣读的文章题名为Observationes de comparatione arcuum curvarum irrectificibilium(关于不可求长的曲线弧长的比较研究)，次年递交的文章则是关于微分方程 $ \frac{m\,}{\sqrt{1-x^4}}\mathrm{d}x=\frac{n\,}{\sqrt{1-z^4}}\mathrm{d}z $ 的研究。这两篇文章在1761年发表于圣彼得堡的期刊Novi Commentarii academiae scientiarum Petropolitanae第六卷上。我们在这里就深入这两篇文章关于双纽线积分的部分，看一看Euler在Fagnano的基础上添加了哪些自己的东西。

[注：1761年这卷期刊的前面近400页全是Euler的各种文章。]

---

我们把时间顺序倒转一下，先从Euler 1753年宣读的文章开始，因为这篇文章中关于双纽线积分的内容反倒是比1752年中的关键内容来得自然。1752年5月30日，Euler在给Goldbach的信件末尾提到了以下两件事实(它们形式上的相似不可能不引起Euler的注意)：

1. $ \frac{1}{\sqrt{1-x^2}}\mathrm{d}x=\frac{1}{\sqrt{1-y^2}}\mathrm{d}y $ 的一组解可以这样表示：

$ y^2+x^2=c^2+2xy\sqrt{1-c^2} $

2. $ \frac{1}{\sqrt{1-x^4}}\mathrm{d}x=\frac{1}{\sqrt{1-y^4}}\mathrm{d}y $ 的一组解可以这样表示：

$ y^2+x^2=c^2+2xy\sqrt{1-c^4}-c^2x^2y^2 $

第一个方程容易理解，它来自正弦函数的和差角公式。但对于第二个方程，Euler并没有正弦函数这样的现成工具可以用，至少他本人在1753年的文章里是这么认为的。按Euler自己的说法，他是靠猜测得到这个方程的代数解的。Euler可能的合情推理是什么呢？

• 根据Fagnano的结果，我们知道第二个方程有代数解 $ x^2y^2+x^2+y^2=1 $ ;

• 交换x,y, 方程不变。因此方程的代数解 $ \phi(x,y)=0 $ 左侧应当是x,y的对称多项式。

• 根据上篇Bernoulli的结果，我们可以得到解 $ x^2y^2+1=0 $ ;

• $ x=y $ 是平凡解。我们把它写成对称的形式，也就是 $ x^2+y^2-2xy=0 $ ;

• [重要]上面的解都是特解。根据这些特解，可以假设，包含这些解的最简单的多项式方程应当有以下形式： $\alpha(x^2+y^2)=2\beta xy+\gamma x^2y^2+\delta$

• 有了这个观察之后，剩下的就是在方程两侧取微分，并联立原方程求待定系数。结果是 $ \alpha^2=\beta^2+\gamma^2,\gamma+\delta=0. $ 走到这一步，Euler的结果就是显然的了；

• Euler并未止步于此。同样的方法可以外推到稍微复杂一些的微分方程 $ \frac{1}{\sqrt{1+mx^2+nx^4}}\mathrm{d}x=\frac{1}{\sqrt{1+my^2+ny^4}}\mathrm{d}y $ .前面的一切推理仍然适用。此时 $ n\beta^2=n\alpha^2+\gamma^2+m\alpha\gamma,\gamma=n\delta $ ；

• 根据Weil的记载，Euler后来甚至走得更远。他认为如果作分式线性变换 $ x\mapsto\frac{ax+b}{cx+d} $ 可以把更一般的微分形式 $ \frac{1}{\sqrt{A+Bx+Cx^2+Dx^3+Ex^4}}\mathrm{d}x $ 化为 $ \frac{1}{\sqrt{1+mx^2+nx^4}}\mathrm{d}x $ 。Legendre后来证明在复数域上这总是可行的。

• Euler试图给出解 $ y^2+x^2=c^2+2xy\sqrt{1-c^4}-c^2x^2y^2 $ 的几何意义。我们已经知道 $ \frac{1}{\sqrt{1-u^4}}\mathrm{d}u $ 是弹性曲线的弧长微分。依照Euler原文中示意图(如下所示)，如果M点横坐标为x，那么弧长AM等于 $ \int_{0}^{x}\frac{1}{\sqrt{1-u^4}}\mathrm{d}u $ 。那么自由常数c与弧长的关系是什么？我们如果假设Fig.2 中d点的横坐标是x，m点横坐标是y，它们满足上面的代数关系。那么根据微分方程 $ \frac{1}{\sqrt{1-x^4}}\mathrm{d}x=\frac{1}{\sqrt{1-y^4}}\mathrm{d}y $ ，我们知道弧am-弧ad=常数(为什么？)。令x为0，此时d点与a点重合，而由微分方程的代数解我们可以确定，待定常数即为d点横坐标为c时的弧长ac。

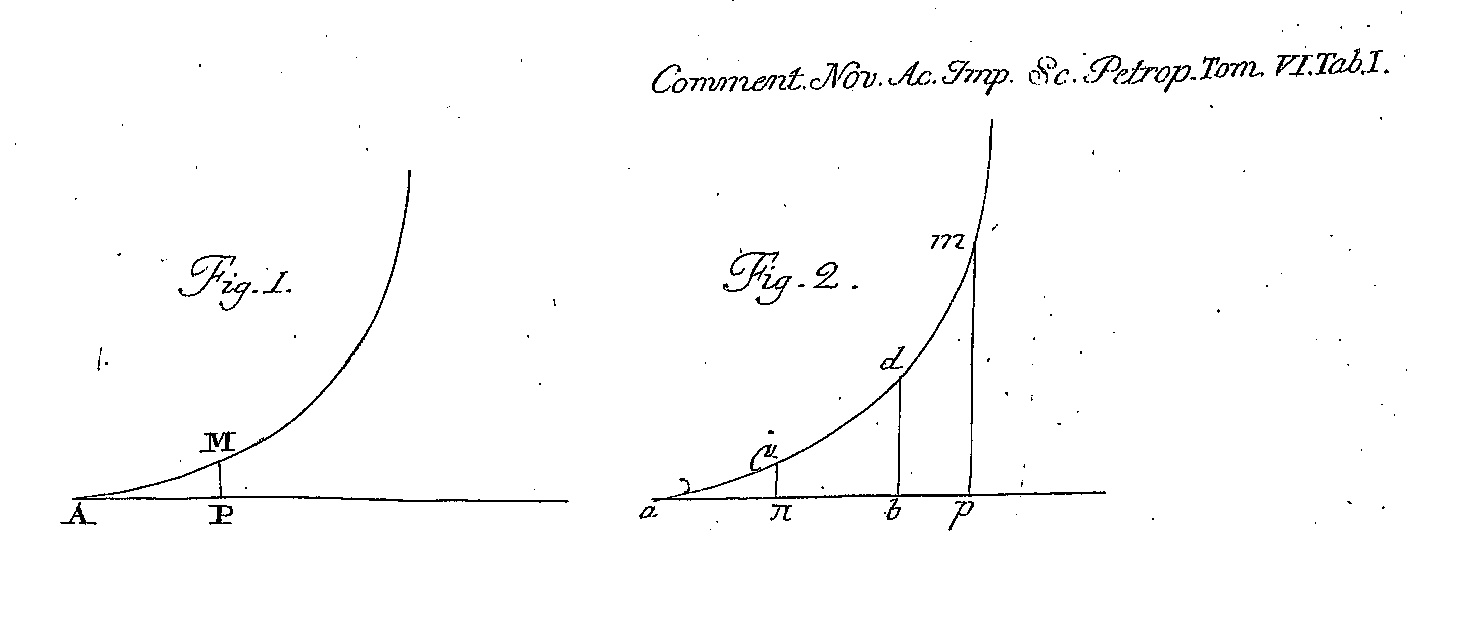
Euler 1752年论文插图

• 我们重新表述一下Euler的结论。如果 $ y^2+x^2=c^2+2xy\sqrt{1-c^4}-c^2x^2y^2 $ ，或者说 $ y=\frac{x\sqrt{1-c^4}+c\sqrt{1-x^4}}{1+c^2x^2} $ ,那么我们就有Euler[关于双纽线]的加法定理 $ \int_{0}^{y}\frac{1}{\sqrt{1-u^4}}\mathrm{d}u=\int_{0}^{x}\frac{1}{\sqrt{1-u^4}}\mathrm{d}u+\int_{0}^{c}\frac{1}{\sqrt{1-u^4}}\mathrm{d}u $ ，正是弧长间的和差关系。

---

Weil以及Alfred Enneper(Elliptische functionen, Theorie und geschichte)在其关于椭圆函数早期发展的历史中都提到，Euler在更早些时候就已经提出了如下定理：

定理(Euler, 1752)：设 $ z $ 的代数函数 $ u $ 满足微分方程 $ \frac{1}{\sqrt{1-u^4}}\mathrm{d}u=\frac{n}{\sqrt{1-z^4}}\mathrm{d}z $ ，其中 $ n $ 是某个正整数。那么下面关于 $ u,z $ 的代数函数 $ s $

$ s=\frac{z\sqrt{\frac{1-u^2}{1+u^2}}+u\sqrt{\frac{1-z^2}{1+z^2}}}{1-uz\sqrt{\frac{1-u^2}{1+u^2}\frac{1-z^2}{1+z^2}}} $ 满足 $ \frac{1}{\sqrt{1-s^4}}\mathrm{d}s=\frac{(n+1)}{\sqrt{1-z^4}}\mathrm{d}z $ 。

这与上面加法定理中的式子是完全等价的，但是形式上远比后来提出的那个要复杂。Euler是怎么得到这个表达式的？关于这个Euler只有一点点提示[译文来自这里]：

Primum quidem tentando elicui, si arcus simpli corda sit $ =z $ , tum arcus tripli cordam fore $ =\frac{z(3-6z^4-z^8)}{1+6z^4-3z^8} $ verum postea rem sequenti modo generaliter expediri posse intellexi.

首先我通过尝试得到，当[双纽线(从原点到某点的)]弧的[坐标](注：这里指极坐标的半径坐标)等于 $ z $ ，那么三倍弧长对应的坐标是 $ =\frac{z(3-6z^4-z^8)}{1+6z^4-3z^8} $ ，不过我后来明白了可以用下面的方法处理一般的情况。

紧接着Euler就提出了上面的定理。之后都是大段的验证，至于动机一概不提。Weil以及Enneper也没有猜测Euler本人是怎么归纳出定理中的函数的。不过我们可以根据蛛丝马迹，猜一猜Euler的思考过程(当然,完全不能保证这些猜测就是Euler本人当年的思路)。

---

[私货时间]

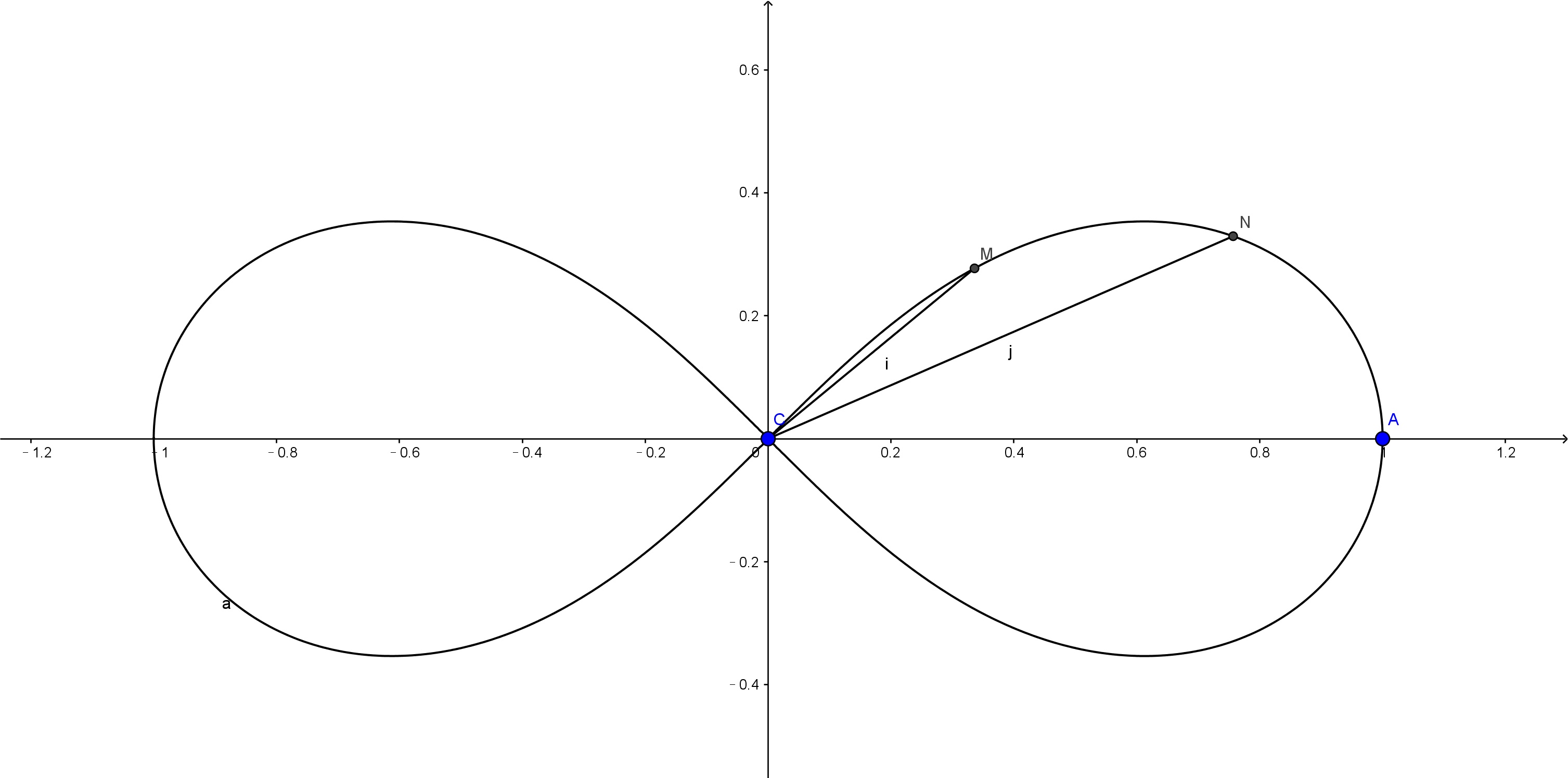
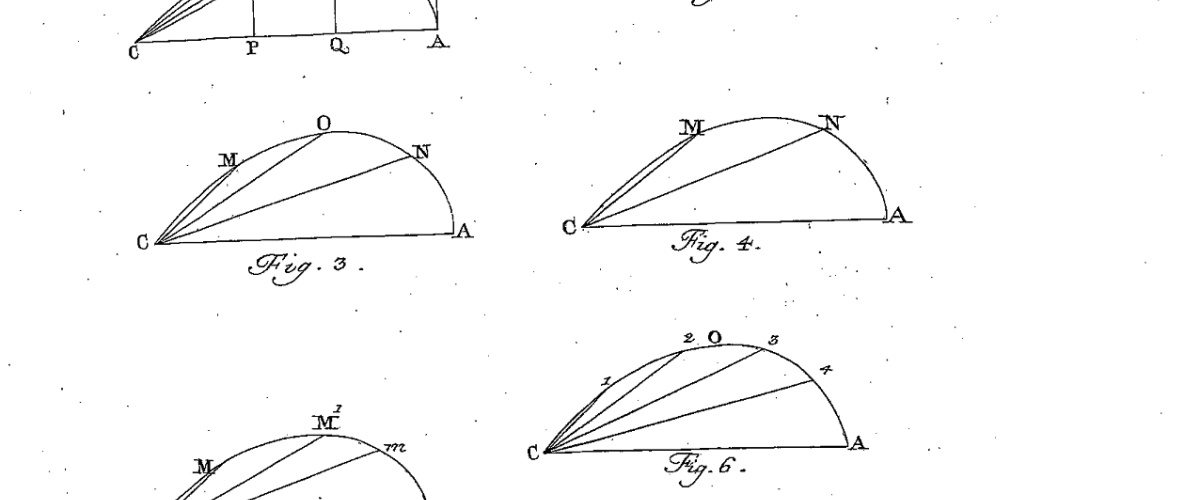
双纽线三等分示意

0. 有理由猜测，Euler试图把微分方程 $ \frac{1}{\sqrt{1-x^2}}\mathrm{d}x=\frac{n}{\sqrt{1-z^2}}\mathrm{d}z $ 的性质外推到 $ \frac{1}{\sqrt{1-x^4}}\mathrm{d}x=\frac{n}{\sqrt{1-z^4}}\mathrm{d}z $ 。这是所有推理的开端。

1. 如上图所示，假设双纽线在第一象限的弧CA被点M, N三等分。Fagnano根据自己的文章中的定理，可以得到如下结论(为什么？)：

如果线段CM=z，CN=x，那么 $ x^2=\frac{4z^2(1-z^4)}{(1+z^4)^2}=\frac{1-z^2}{1+z^2} $ 。

2. (0)中的第一个方程对应的是正弦的n倍角公式。对应的解为 $ x^2=R_n(z) $ ,R是多项式。根据Fagnano的二倍弧长公式，对(0)中第二个方程一个合理的猜测是：它的解为 $x^2=\frac{\bar P_n(z)}{\bar Q_n(z)}$ 。微分方程中 $x\mapsto\pm ix,z\mapsto\pm iz$ ,方程不变，其中i是虚数单位。因此我们可以进一步猜想 $ x^2=\frac{z^2P_n(z^4)}{Q_n(z^4)} $ (P,Q是互质的多项式)

3. (1)中x的值有两种可能。 消去z，我们有 $ x=0 $ 或 $ x^8+6x^4-3=0 $ 。所以假想的三倍弧长公式中的多项式 $ P_3 $ 可以被 $ z^2+6z-3 $ 整除(为什么？)。另外(1)中的 $ z $ 满足方程 $ z^2=1 $ 或 $ (1+z^4)^2=4z^2(1+z^2)^2 $ 。

4 . 将猜测解代回其对应的微分方程，整理可得

$ T^2=\frac{4n^2P(z^4)Q(z^4)(Q^2(z^4)-z^4P^2(z^4))}{1-z^4} $

$ T $ 是关于 $ z^4 $ 的多项式。因此有(3-1)=2种可能

a. $ P=f_1^2,Q=f_2^2,Q^2-z^4P^2=(1-z^4)f_3^2 $

b. $ P=(1-z^4)f_1^2,Q=f_2^2,Q^2-z^4P^2=f_3^2 $

$ f_1,f_2,f_3 $ 都是 $ z^4 $ 的多项式。对于n为奇数，我们取情形a，n为偶数当取情形b(为什么？)。

5. 根据上面(3)(4)的结论，可以猜测，当n=3， $ f_1(z^4) $ 含因子 $ z^8+6z^4-3 $ ,而 $ f_3(z^4) $ 含因子 $ (1+z^4)^2\pm4z^2(1+z^2)^2 $ 。 综合这些考虑，我们可设 $ Q-z^2P=(1-z^2)((1+z^4)^2-4z^2(1+z^2)^2)^2g^2 $ , $ g $ 是 $ z^2 $ 的多项式。这个式子还可以化简： $f_1-zf_2=(1-z)(1+z^4\pm 2z(1+z^2))^2h^2$ , $ h $ 是 $ z $ 的多项式。取正号可以保证展开时消去的项尽可能地多。展开 $(1-z)(1+z^4+ 2z(1+z^2))^2$ 并重组各项，不难得到它的值为 $ (1-3z^8+6z^4-z(z^8+6z^4-3)) $ 。剩下验证性的工作不言自明。

6. 上篇中Fagnano 1718年发表的文章中的定理可以这样叙述：

如果 $ x,x^\prime\in(0,1) $ ,且 $ x^\prime=\sqrt{\frac{1-x^2}{1+x^2}} $ ，那么 $ \int_{0}^{x}\frac{1}{\sqrt{1-z^4}}\mathrm{d}z+\int_{0}^{x^\prime}\frac{1}{\sqrt{1-z^4}}\mathrm{d}z=\int_{0}^{1}\frac{1}{\sqrt{1-z^4}}\mathrm{d}z $

三角函数中与之平行的结论自然是

如果 $ x,x^\prime\in(0,1) $  ,且 $ x^\prime=\sqrt{1-x^2} $ ,那么

$ \int_{0}^{x}\frac{1}{\sqrt{1-z^2}}\mathrm{d}z+\int_{0}^{x^\prime}\frac{1}{\sqrt{1-z^2}}\mathrm{d}z=\int_{0}^{1}\frac{1}{\sqrt{1-z^2}}\mathrm{d}z $

因此，在这里x'之于x正如三角函数中余弦之于正弦，下文就统一采用这一记号。

7. 正弦的(n+1)倍角公式可以由n倍角公式导出。换言之，Euler 1752年定理的三角函数版本自然是 $ s=z\sqrt{1-u^2}+u\sqrt{1-z^2} $ 。对于双纽线积分，我们的第一猜测自然是把三角函数相应的表达式全部替换为双纽线版本。也就是 $\bar s=z\sqrt{\frac{1-u^2}{1+u^2}}+u\sqrt{\frac{1-z^2}{1+z^2}}$ 。

8. 这个表达式靠不靠谱呢？根据Fagnano的公式以及上面的推理，我们可以计算出n=1,2,3,4倍弧长公式及其相关表达式，如下表所示：

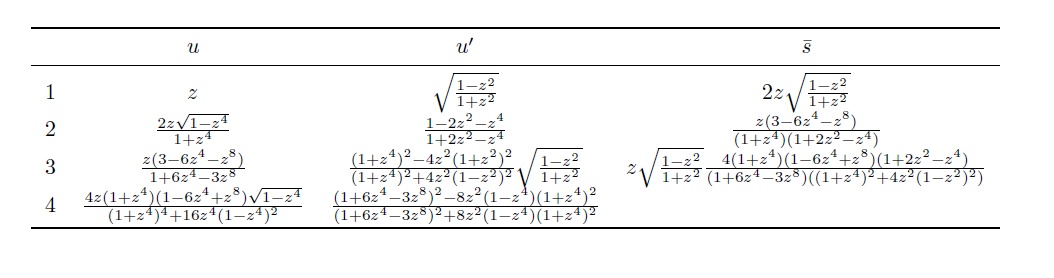
对于2,3,4倍弧长公式这个猜想不算太离谱，至少 $ \bar{s} $ 和实际的弧长公式在分子上有数目不少的公因子。我们可以重写一下表达式： $ s=\bar{s}/K $

$$ \begin{align}K&=\frac{1+z^4}{1+z^2}\qquad(n=1)\\K&=\frac{1+6z^4-3z^8}{(1+z^4)(1+2z^2-z^4)}\qquad(n=2)\\K&=\frac{((1+z^4)^4+16z^4(1-z^4)^2)(1+2z^2-z^4)}{(1+z^2)(1+6z^4-3z^8)((1+z^4)^2+4z^2(1-z^2)^2)}\qquad(n=3)\end{align} $$

第一个表达式很容易重写为 $ 1-z^2{z^\prime}^2 $ 。这形式不够对称，可以把它重写为 $1-uzu^\prime z^\prime$ 。用这个形式去验证我们得到的另两个表达式，结果也是完全吻合的。这就引出Euler的

$$s=\frac{u^\prime z+uz^\prime}{1-uzu^\prime z^\prime}$$

以及与之相伴的$ s^\prime=\sqrt{\frac{1-s^2}{1+s^2}}=\frac{\sqrt{1-u^4}\sqrt{1-z^4}-2uz}{1+u^2+z^2-u^2z^2} $ 。如果我们把它和余弦函数的和差公式做对照，那么我们就被引导到它的对称形式

$$s^\prime=\frac{u^\prime z^\prime-uz}{1+uzu^\prime z^\prime}$$

这两个公式可以说是1752年论文中最重要的公式。如果Euler1752年宣读的论文和1761年印刷稿内容完全一致的话，那只能凸显这个人的无以伦比的力量：在一个月内就能把理论推进到如此地步，天下奇才也。

[补注: Legendre很喜欢用Euler的微分方程的变体，也就是 $\frac{1}{\sqrt{(1-x^2)(1-k^2x^2)}}\mathrm{d}x=\frac{1}{\sqrt{(1-y^2)(1-k^2y^2)}}\mathrm{d}y,(k^2\neq 1).$ 根据Harold M. Edwards的这篇文章(其实利用我们上面的推理也可以很快发现这一点)，双纽线积分加法定理的两个对称形式可以推广到这一类方程上去。此时我们有$ x^\prime=\sqrt{\frac{1-x^2}{1-k^2x^2}} $ 且 $s=\frac{u^\prime z+uz^\prime}{1+k^2uzu^\prime z^\prime},s^\prime=\frac{u^\prime z^\prime-uz}{1-k^2uzu^\prime z^\prime}$ 。这些公式对应的正是亏格为1的曲线 $x^2+y^2=1+k^2x^2y^2 $ 上的加法群！]

---

利用Euler的公式，可以得到双纽线任意整数倍的弧长公式。Fagnano声称自己可以找到5等分点，但是那是间接用弧长的2倍公式得到，他本人并不知道5倍弧长公式是什么。我们利用Euler的公式可以算出，当n=5时对应的公式为

$$u=z\cdot\frac{5 - 2 z^4 + z^8}{1 - 2 z^4 + 5 z^8}\cdot\frac{1 - 12 z^4 - 26 z^8 + 52 z^{12} + z^{16}}{1 + 52 z^4 - 26 z^8 - 12 z^{12} + z^{16}}$$

对照我们上边得到的表，我们可以观察到： 对于正整数 $ n$而言，$u,u^\prime $ 中必有一个是Q上的有理函数。分子的根对应双纽线在右半平面部分的n等分点。这些有理函数的分子的次数分别是1,4,9,16,25,...。Euler去世后十多年，有一位二十岁上下的青年观察到了这一点。他在自己的小日记本上写下[译文来自这里的英译]:

Cur ad aequationem perveniatur gradus $ nn^{\mathrm{ti}} $ dividendo curvam lemniscatam in $ n $ partes.

为什么 $ n $ 等分双纽线会带来 $ n^2 $ 次方程。

那是1797年3月19日。Euler也没有注意到的双纽线的性质，从这个问题发端。