量子图
2016-01-01
7421
你怎样确定一束光是否以和相机工作原理一样正确的方式在一面镜上反射？你可能会画一幅图来了解所发生的事情，写下一些方程，做一些计算，取出这个结果。这就是物理学一般的做法，而且自牛顿方程的时代起一直如此：计算，结果。
“费恩曼跳过了这一切，”普林斯顿高等研究院的物理学家弗里曼·戴森说。“他只是记下图，然后写出答案，别无任何方程。”
戴森在谈论理查德·费恩曼，回顾他四十年代末期在康奈尔大学的时间。当时，量子电动力学（QED），这个用来描述光与物质相互作用新开发的理论，正深陷困境。即使计算电子和光子之间的最简单相互作用也是如此的复杂，它甚至吓坏了那些最有成就的物理学家。加上其它的问题，这将量子电动力学的整个大厦扔向疑问（见前面的文章）。费恩曼现已称为费恩曼图的棒状图形，出手相救，它们竟然成为物理学中一个无处不在的工具。
“费恩曼是一个伟大的人物，”戴森回忆道。 “费恩曼给人的快乐是，他完全直言不讳，关于你或其它任何东西他总说真话。如果我想去和费恩曼讲话，我就走进他的房间，他会说'走开，你不看我正忙着吗？’另一次我来了，他很友好，所以我知道他真的欢迎我。我非常喜欢他，因为他是一个真正的演员。他只是喜欢表演，因此必须有一个观众。”
关于费恩曼著名的不敬有许多故事，也许是这些同样的不敬使他跳过形式化，用图形来思维。作为一个例子，考虑散射掉对方的两个电子。你也许会天真地认为它们是微小的台球：如果你知道它们各自的行进速度和方向，你可以推断出它们是否相撞，并将预见在碰撞后的任何给定时间它们会在哪里。但在量子物理里事情并不那么简单。电子的行为既像粒子又像波：不可能以同等精度确定它们两者的位置和动量，他们不沿直线传播，你甚至无法知道两个电子分开。所有你能做的就是确定出两个电子会以特定方式散射的概率（查看我们介绍量子力学关于薛定谔方程的文章）。
Richard Feynman (1918-1988)
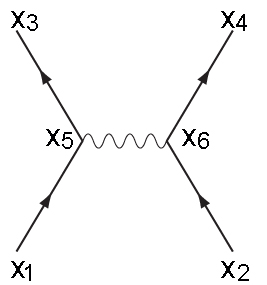图1：该图像是一个费曼图的电子散射
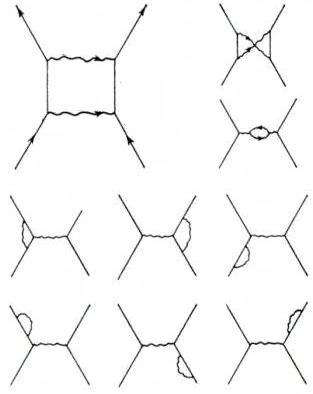此图像是从理查德·费曼图的量子电动力学时空方法这一文章中改编过来的,显示了两个电子可以通过交换两个光子进行散射的所有方式。版权属于美国物理学会(2013)。
Richard Feynman (1918-1988)更重要的是，电子不是由碰撞，而是通过交换虚光子散射。例如，一个电子能发出一个虚拟光子，另一个能吸收它。吸收和发射改变每个粒子的速度和方向：这就是散射。计算两个电子在时空点$x_1$和$x_2$出发且散射后在$x_3$和$x_4$点结束的概率，涉及到所述第一个电子行进到点$x_5$并在那里发出光子，然后行进到$x_3$点的概率，以及另外那个电子行进到点$x_6$后并在那里吸收它，然后行进到$x_4$点和概率，再加上虚光子经过$x_5$到$x_6$旅程的概率。更有甚者，因为我们不能确定电子的轨迹，点$x_5$和$x_6$可以在时空的任何地方。（这个例子摘自费恩曼的书《量子电动力学---光与物质的奇怪理论》）
图1：该图像是一个费曼图的电子散射把所有这些因素考虑在内提供了有关散射事件概率的一个笨拙表达式，它包括二重积分和考虑到不同概率的许多不同项。所有都为了捕捉到这个理应简单的情形。
而这还不是全部。两个电子可通过以复杂方式交易任何数量的虚拟光子来散射。例如，所发射的光子可能变成由一个虚拟电子和一个虚拟抗电子（通常称为正电子）构成的一对，然后彼此抵消，形成一个新的光子，后者被第二个电子吸收。所有可能的相互作用都需要加以考虑，这导致了又长又复杂的数学表达式，即使是最勤奋的会计师也难以跟踪。犯错、遗漏和重复计算的范围是巨大的。
但是在费恩曼的心目中，上述的二重积分变成了一个简单的示意图，如图1所示。乍一看，这看起来像一个真正物理过程的面，但事实并非如此。横轴表示空间（我们假定粒子按一维行进），纵轴表示时间。因此，静止几秒钟的一个粒子（实际上它不会这样，但让我们暂时假设这样），将由代表时间流逝的垂直线表示。更有甚者，直线和蠕动线不代表粒子的真实轨迹，而仅仅是粒子首先在空间和时间中的一点，然后在另外一个点的概率。（如果您想了解更多信息，{ Quantum Diaries }有关于费恩曼图的一个出色介绍。关于费恩曼图的分散体和物理应用的迷人叙述，可见大卫·凯瑟(David Kaiser)的书{ Drawing Theories Apart }）
然而，物理学家从这样的图中可以很容易地读出数学。 “每当你看到费恩曼图上的一条直线，它正是你的相应公式里的唯一表达式，”麻省理工学院物理史家大卫·凯瑟说。“当你看到一条蠕动的线，它刚好有这种表达式。一旦你学会了几个简单的规则，它变得令人吃惊的简单。”所有其它可能的相互作用，涉及多个虚拟粒子，都具有类似的图。当你考虑越来越多的虚粒子时，它们的数目非常迅速地变大，但是与仅仅注意到数学相比，跟踪它们更容易。
此图像是从理查德·费曼图的量子电动力学时空方法这一文章中改编过来的,显示了两个电子可以通过交换两个光子进行散射的所有方式。版权属于美国物理学会(2013)。
从那以后，费恩曼的辉煌图已经成为物理学家的工具包中不可或缺的一部分，以至于人们有时会误认为它们是现实的文字描写，而不是纸上作为方程速记画出的图像。“我喜欢这个助记符，‘让我拿放大镜看看大自然，我将看到的是费恩曼图，’”大卫·凯瑟说。“这是一个美妙的滑动，我们正在画的图形如同一只棒球通过空间和时间翻腾。费恩曼绝没有被迷惑所烦恼。他会说，实际上，对他而言这么想有道理。他经常非常拟人化地说，“我是这个电子。我坐在这里，我被这个光子猛击，当然我正被弄掉。”
费恩曼的直观方法并不能掩盖他的物理洞察力，但它确实妨碍沟通。当费恩曼在一次会议上首次提出他的图时，观众并没有留下深刻的印象。他无法精确解释直线和蠕动线应该怎样翻译成方程式，并表明他的图并不能掩盖更复杂的情况。“费恩曼在某种意义下有正确的规则，但那时还不清楚它们的一般性到底如何，”凯瑟说。“它们真的来自量子场论的中心地带，还是仅仅代表一些特殊情况？”
是弗里曼·戴森最终理清了这些规则。“戴森证明，如果我们把量子场论作为联合量子力学和狭义相对论的第一次努力，那么这就是转换规则应该是什么的唯一固定的东西，”凯瑟说。“因此是戴森把它们系统地阐明出来，然后显示它们确实成立。然后，运用规则会变得非常简单。”
费恩曼的图帮助解决了困扰QED的一个问题：对所有可能涉及任意数量虚拟粒子的复杂方式保持跟踪，并在计算时考虑到这些。但也有另外一个问题：甚至一个虚粒子也可以带有任意值的能量。将这种无限制的能量考虑在内意味着，仅仅涉及一个虚粒子的计算也会以无穷作为答案。施温格和朝永对这难题已经各自独立地提供了一个解决方案：不试图获得在裸粒子（即对自己而言的粒子），而是应该永远只考虑它及其虚拟的随行物，并在计算中使用有效量（见前面的文章）。费恩曼本人也已制定了一个类似的方法。
但问题是，这三个人原本只能够驯服计算中涉及一个或两个虚拟粒子的无穷大。当时尚不清楚该方法对更大的数目是否工作。具有量子物理技术数学家认识的戴森前来救援，证明费曼、施温格和朝永的办法适用于任何数量的虚拟粒子。“我有量子场论的工具，而其他人没有，”戴森说。 “我可以把它们放在一起，并证明这一切都是很简单的。这真是一个惊人的好运气。从一个不起眼的学生，我一下子成了大人物。”
戴森2005年, Jacob Appelbaum
戴森2005年, Jacob Appelbaum费恩曼的图和戴森的理论监管促进了乐观情绪：计算变得更容易，无穷大可被驯服，量子电动力学的难题似乎告破了。接下来的挑战是同样的想法应用到自然界的其它力。但是事实证明，这是一个完全不同的故事。我们将在{ Plus }中即将出现的另一系列文章内探讨。
