美国高中数学测验 AMC12之机率问题(下)
几何机率
前述两节的问题皆建立在样本点个数为可数时的情况,接下来将介绍一不可数的无穷样本空间$S$且利用此空间的一些几何测量$m\left(S\right)$,例如长度、面积、或者体积,来求$A$事件的机率。而$A$事件的机率可用$A$事件之几何测量与样本空间$S$之几何测量的比例来计算,其形式有下列三种:
注:我们必须假设一不可数无穷样本空间S满足均匀性质,这样才能做以上的几何机率。
几何测量—长度
所谓长度的几何测量,表示其无穷样本空间可用一线段、数线或是时间轴$\cdots$等表示,则考虑某事件的机率时,只需探讨此事件所占的线段(或数线)与样本空间相对的长度比值即可,下 列为利用长度测量来求的机率问题。
例1.(1972 AMC12 #17) 随机将一条线切为两段,试问较长的一段至少是较短的一段的x倍(其中x¸1)的机率为多少?
- (A)$\dfrac{1}{2}$
- (B)$\dfrac{2}{x}$
- (C)$\dfrac{1}{x+1}$
- (D)$\dfrac{1}{x}$
- (E)$\dfrac{2}{x+1}$
解:(E)假设线段$AB$被切为两段,若较长一段(标记为$l_1$,长度为$sx$)为较短一段(标记为$l_2$,长度为$s$)的$x$倍,则线段$AB$总长度为$(x+1)s$,因此切点会落于$l_2$中的机率为\dfrac{1}{x+1}。但因线段的切法可能为($l_1$,$l_2$)或是($l_2$,$l_21$)两种情况,如下图

故所求机率为$\dfrac{2}{x+1}$。
例2.(2007 AMC12B #13)有一交通号志以下列的循环重复的运作:绿灯30秒,然后黄灯3秒,之后再转红灯30秒。利亚随机挑选三秒钟的区间去注视号志灯,试问号志灯在转换颜色时,利亚正在注视的机率为多少?
- (A)$\dfrac{1}{63}$
- (B)$\dfrac{1}{21}$
- (C)$\dfrac{1}{10}$
- (D)$\dfrac{1}{7}$
- (E)$\dfrac{1}{3}$
解:(D)由题意知,交通号志运作一循环需时63秒,而若利亚所注视的时间在当绿灯转变为黄灯、黄灯转变为红灯或红灯转变为绿灯的前三秒钟内,则利亚会看到号志颜色正在转变,如下图所示

故所求机率为
例3.(2009 AMC12B #18) 瑞吉儿与罗伯特在一圆形的跑道上跑步,其中瑞吉儿以逆时钟方向跑且跑完一圈需时90秒,而罗伯特以顺时钟方向跑且跑完一圈需时80秒。此两人同 时在同一起跑线起跑,有一站在跑道内的摄影师,以起跑线为中心线,对$\dfrac{1}{4}$的跑道做拍照,试问在两人起跑后的10分钟到11分钟间,照片会同时拍到此两人的机率为何?
解:(C) 因瑞吉儿跑一圈需要 90 秒, 所以当在第十分钟的时候, 她已经跑了 $6\dfrac{2}{3}$ 圈, 为下图标 示之位置, 则其进入到离开摄影师的拍照范围时间为第十分钟的 18.75 秒到第十分钟的 41.25 秒 (以”$\cdots$ ” 表示瑞吉儿); 而罗伯特跑一圈需要 80 秒, 所以当在第十分钟的时候, 他已经跑了$7\dfrac{1}{2}$ 圈, 为下图标示之位置, 则其进入到离开摄影师的拍照范围时间为第十分钟的 30 秒到第十分钟的 50 秒 (以”---” 表示罗伯特)。
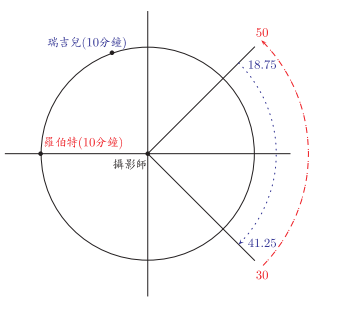
所以在第十分钟第 30 秒到第 41.25 秒此两人皆在此拍摄区域内, 故所求机率为
几何测量—面积
面积的几何测量,表示其无穷样本空间可用平面区域来表示,其样本点皆落于区域中,则考虑某事件的机率时,只需探讨此事件所占的区域与样本空间的区域相对面积比值即可,下列为利用面积测量来求的机率问题。
例4.(2001 AMC12 #17) 已知五边形$ABCDE$的顶点为$A(0,2),B(4,0),C(2\pi+1,0),D(2\pi+1,4)及E(0,4)$,现从这五边形内部中任取一点$P$,试问$\angle APB$是钝角的机率为多少?
- (A)$\dfrac{1}{5}$
- (B)$\dfrac{1}{4}$
- (C)$\dfrac{5}{16}$
- (D)$\dfrac{3}{8}$
- (E)$\dfrac{1}{2}$
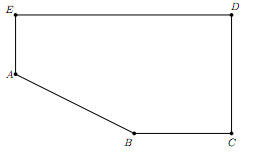
解:(C) 以A,B为直径画一半圆,若点P落于此半圆内,会使得$\angle APB$为钝角,如下图斜线部分
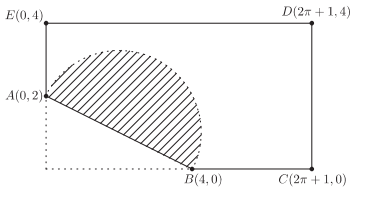
因为$\overline{AB}=2\sqrt{5}$,所以圆半径为$\sqrt{5}$,故所求机率为
例5.(2002 AMC12B #18) 由$(0,0),(2,0),(2,1),(0,1)$四点所围的四边形中任选一点P,试问P到原点的距离小于P到$(3,1)$的距离的机率为多少?
- (A)$\dfrac{1}{2}$
- (B)$\dfrac{2}{3}$
- (C)$\dfrac{3}{4}$
- (D)$\dfrac{4}{5}$
- (E)$1$
解:(C) 设$O(0,0),A(2,0),B(2,1),C(0,1),Q(3,1)$,连接线段$\overline{OQ}$,并做$\overline{OQ}$之中垂线$l$,如下图所示
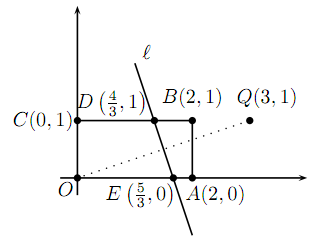
因为在$l$上任一点到$O$与$Q$点距离相等,故点$P$在$l$左方时,会使得$\overline{OP}
例6.(2009 AMC12B #23) 在复数平面上有一区域$S$定义如下:
有一复数$z=x+iy$由区域$S$中均匀且随机的选取,试问$\left(\dfrac{3}{4}+\dfrac{3}{4}i\right)z$亦落于区域$S$中的机率为何?
- (A)$\dfrac{1}{2}$
- (B)$\dfrac{2}{3}$
- (C)$\dfrac{3}{4}$
- (D)$\dfrac{7}{9}$
- (E)$\dfrac{7}{8}$
解:(D) 解法一: 由题意知
欲落于集合$S$中, 表示
即为
将所求得之线性不等式与x,y 之条件绘制如下:
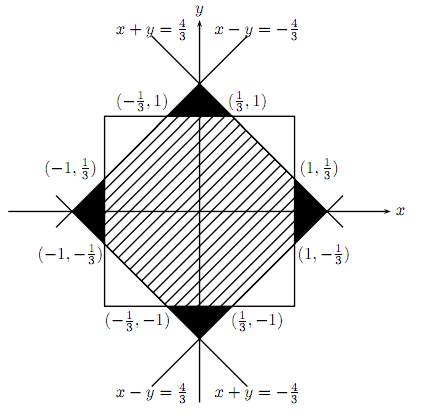
其中斜线部分表示能满足题意要求的x,y所形成的区域,且四块相等之黑色小等腰直角三角形面积为
故所求机率为
解法二:将z及复数$\left(\dfrac{3}{4}+\dfrac{3}{4}i\right)$转换为极式如下:
所以
因此可将$\left(\dfrac{3}{4} +\dfrac{3}{4}i\right)z$视为复数z在复数平面上被旋转$45^\circ$,且长度增为$\dfrac{3\sqrt{2}}{4}$倍,如下图所示:
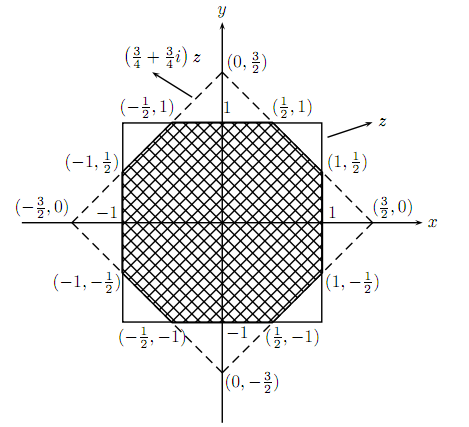
其中实线正方形部分表复数$z$可能的值,虚线正方形部分表示经过旋转放大后可能的值,则图中斜线部分即表示$\left(\dfrac{3}{4}+\dfrac{3}{4}i\right)z$的值亦属于集合$S$,故所求机率为
几何测量—体积
面积的几何测量,表示其无穷样本空间可用平面区域来表示,其样本点皆落于区域中,则考虑某事件的机率时,只需探讨此事件所占的区域与样本空间的区域相对面积比值即可,下列为利用面积测量来求的机率问题。
例4. (2001 AMC12 #17) 已知五边形$ABCDE$的顶点为$A(0,2),B(4,0),C(2\pi+1,0),D(2\pi+1,4)$及$E(0,4)$,现从这五边形内部中任取一点$P$,试问$\angle APB$是钝角的机率为多少?
- (A)$0$
- (B)$0.1$
- (C)$0.2$
- (D)$0.3$
- (E)$0.4$
解:(C) 假设$ABCD$为边长为a之正四面体,其外接球与内切球的球心皆为$O$,半径分别为$r,r'$,而内切球切正四面体一面于$E$点,并有以球心为$O'$半径为$r"$的球同时与外接球与正四面体皆相切,且切外接球于$F$点,因此$C-O-E-O'-F$为共线,如下图
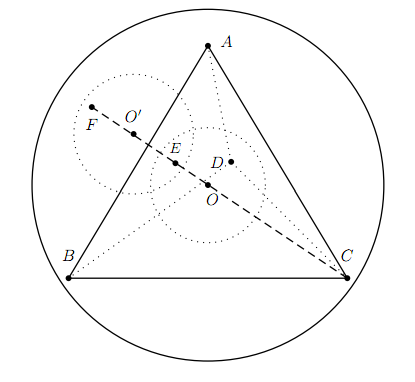
则
所以$r^" = \overline{O'E} =\dfrac{\sqrt{6}}{12}a$, 则 $r : r^': r^" = 3 : 1 : 1$。不失一般性假设外接球体积为$27V$,正四面体内切球的球体积为$V$,与外接球及正四面体相切的球体积为$V$。又因为同时与外接球及正四面体相切的球有$4$个,故所求机率为
注:令外接球与内切球的球心皆为$O$,半径分别为$\overline{OA}=\overline{OC}=r,\overline{OH}=r^'$,且正四面体$ABCD$之边长为a,点$E$为内切球切正四面体的一切点,如下图
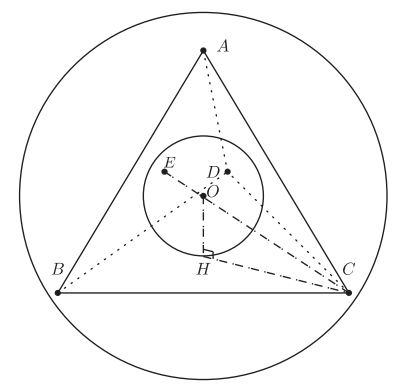
则点$H$必为$\triangle BCD$之重心,所以
由毕氏定理
可求得外接球半径$r=\dfrac{\sqrt{6}}{4}a$,内切球半径$r'=\dfrac{\sqrt{6}}{12}a$。
路径问题
「路径问题」为加法原理与乘法原理的特殊应用,常以走捷径问题或是空间中各式立体图形的行走方式出现,以下为几个路径问题的探讨。
例8.(1982 AMC12 #25) 下图为某城市的一部份地图,小的长方形表示街块(注:一个街块表示东西向二个相邻街道之间及南北向二个相邻街道之间的区域),而其馀部分表示街道。有一学生每天早上都从街口$A$到街口$B$,其行走方向为向东或是向南,在每一个街口选择向东或是向南的机率皆相同,且不会影响其他街口的选择。试问在某一天早上,该名学生通过街口$C$的机率为多少?
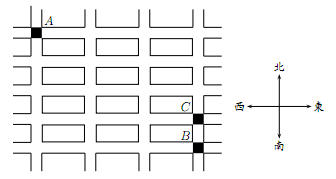
- (A)$\dfrac{11}{32}$
- (B)$\dfrac{1}{2}$
- (C)$\dfrac{4}{7}$
- (D)$\dfrac{21}{32}$
- (E)$\dfrac{3}{4}$
解:(D) 将街口A至B的机率表示如下
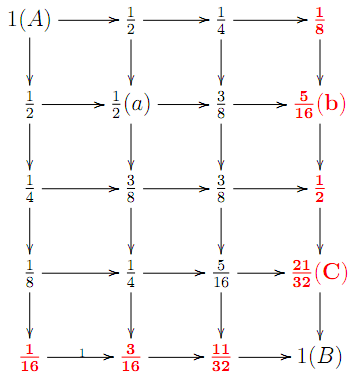
由图可知由街口$A$走到街口$B$中途会通过$C$的机率为$\dfrac{21}{32}$。
以此类推,但在图中的最下方及最右侧两侧的机率计算需特别注意,因需到达街口$B$,故不能向东(向南),只能向南(向东),因此选择走向的机率为1,例如走至(b)之机率为
即表示由A到达B的每一条路机率并不相等(最右侧及最下方),故不能只计算由A到达B的路径。
错误解法:
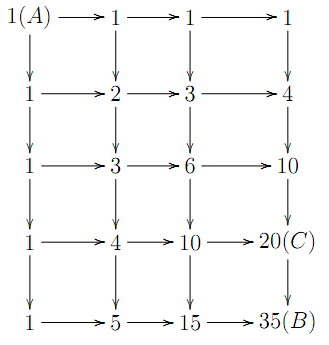
由街口$A$走到街口$B$中途会通过$C$的机率为$\dfrac{20}{35}=\dfrac{4}{7}$。
例9.(2006 AMC12A #20) 一只虫从一个正立方体的某一个顶点开始沿著稜线依下列的规则移动,每次移动均由一顶点开始沿交会于此顶点的三条稜线中之一条稜线移至下一个顶点,每一条稜线被选到的机率相同,且每次选取都是独立的。试问七次移动后,这只虫经过每一个顶点恰好一次的机率是多少?
- (A)$\dfrac{1}{2187}$
- (B)$\dfrac{1}{729}$
- (C)$\dfrac{2}{243}$
- (D)$\dfrac{1}{81}$
- (E)$\dfrac{5}{243}$
解:(C) 假设虫的起始点为正立方体中的$A$点,如下图中所示位
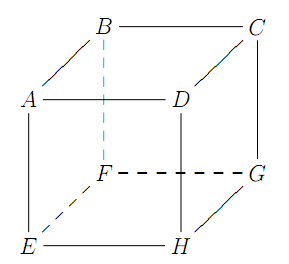
则在$A$点有$3$种方向可以选择行走,假设选择走至$B$,因需$7$次走完全部的顶点,所以不可重复行走走过的路径,故只有$2$种行走方向($C$或$F$)可以选择,以下为走至$C$点后的可能行走方式:
(1) 若下一个行走方向为往下至另一面(G点)时,则其走完全部顶点的走法只有1种,为
如下图所示
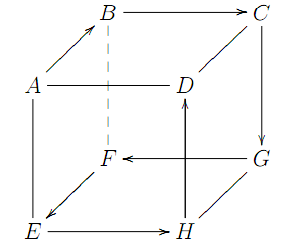
会有$3\times2\times1=6$种走法。
若下一个行走方向为往下至另一面(D点)时,则其走完全部顶点的走法只有2种,为
如下图所示
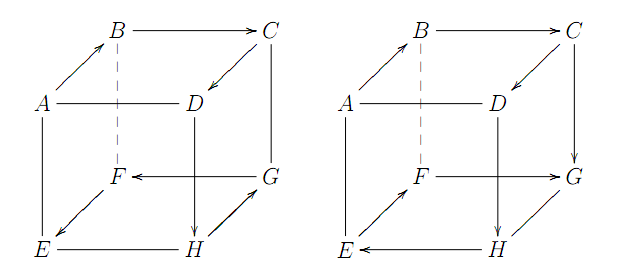
会有$3\times2\times2=12$种走法。
综合上述情况, 所求机率为
习题
机率
习题10. (1963 AMC12 #36) 假设某人最初有64元,和另一人打赌六次,结果输赢各三次,且输赢的机会相等,若不考虑输赢的先后顺序。若赌金为每一次赌博时剩馀钱之半,试问此人最后的输赢情况为何?
- (A) 输$27$元
- (B) 赢$27$元
- (C) 输$37$元
- (D) 不赢也不输
- (E) 输、赢依据输赢所发生之次序而定
答案: C
习题11. (1970 AMC12 #31) 如果由所有的五位数字的集合中随机的挑选出一个数,使得各位数字和为43,试问这个数可以被11整除的机率为多少?
- (A)$\dfrac{2}{5}$
- (B)$\dfrac{1}{5}$
- (C)$\dfrac{1}{6}$
- (D)$\dfrac{1}{11}$
- (E)$\dfrac{1}{15}$
答案: B
习题12. (1981 AMC12 #26) 艾丽丝、鲍勃和卡罗尔轮流投掷一颗骰子,由艾丽丝先开始,按著是鲍勃,然后是卡罗尔,然后又是艾丽丝,以此循环轮流投掷骰子,试求卡罗尔为第一个掷出6点的机率为多少?(任何一次投掷出6点的机率都是$\dfrac{1}{6},与任何其他次投掷的结果无关)
- (A)$\dfrac{1}{3}$
- (B)$\dfrac{2}{9}$
- (C)$\dfrac{5}{18}$
- (D)$\dfrac{25}{91}$
- (E)$\dfrac{36}{91}$
答案: D
习题13. (1984 AMC12 #19) 在一盒子内装有$11$颗球,球上分别标有号码$1,2,\cdotd,11,$若随机地从盒中抽出$6$颗球,试问抽出的球的号码之和是奇数的机率是多少?
- (A)$\dfrac{100}{231}$
- (B)$\dfrac{115}{231}$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{118}{231}$
- (E)$\dfrac{6}{11}$
答案: D
习题14. (1988 AMC12 #28) 投掷一枚“不公正”的硬币,已知其正面朝上的机率为$p$。设$w$为在$5$次互相独立的投掷中,正面朝上的次数正好是$3$次的机率,若$w=\dfrac{144}{625},则p值为
- (A) p 必为$\dfrac{2}{5}$
- (B) p 必为$\dfrac{3}{5}$
- (C) p 必大于$\dfrac{3}{5}$
- (D) p无定值
- (E)没有p值使得$w =\dfrac{144}{625}$
答案: D
习题15. (1990 AMC12 #18) 从集合$S=\{1,2,\cdots,99,100\}中先随机挑选出一数字$a$,再从集合$S$中随机挑选出一数字$b$,试求$3^a+7^b$的个位数字为$8$的机率?
- (A)$\dfrac{1}{16}$
- (B)$\dfrac{2}{8}$
- (C)$\dfrac{3}{16}$
- (D)$\dfrac{1}{5}$
- (E)$\dfrac{1}{4}$
答案: C
习题16. (1991 AMC12 #13) 三匹马$x$,$y$与$z$之间进行一场比赛,且必会分出名次,若不利于$x$胜的架势是$3$对$1$,不利于$y_4$胜的架势是$2$对$3$,试问不利于$z$胜的架势是几对几?(“不利于$H$胜的架势是$p$对$q$”,这句话的意思是$H$胜的机率是$\dfrac{q}{p+q}$,且$p$,$q$互质)
- (A)$\dfrac{1}{16}$
- (B)$\dfrac{2}{8}$
- (C)$\dfrac{3}{16}$
- (D)$\dfrac{1}{5}$
- (E)$\dfrac{1}{4}$
答案: D
习题17. (1992 AMC12 #29) 一个不公正的硬币,掷出正面的机率为$\dfrac{2}{3}$,若掷50次,试求硬币出现偶数次正面的机率。
- (A)$25\left(\dfrac{2}{3}\right)^{50}$
- (B)$\dfrac{1}{2}\left(1-\dfrac{1}{3^{50}}\right)$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{1}{2}\left(1+\dfrac{1}{3^{50}}\right)$
- (E)$\dfrac{2}{3}$
答案: D
习题18. (1994 AMC12 #30) 当投掷n个六面公正骰子得到点数总和为1994之机率与得到点数总和为S的机率相等,试问S的最小值为何?
- (A)$333$
- (B)$335$
- (C)$337$
- (D)$339$
- (E)$341$
答案: C
习题19. (1995 AMC12 #20) 若$a,b,c$为从集合$\{1,2,3,4,5\}$中随机选取出的三个数字(可重复选取),试问$ab+c$为偶数的机率为何?
- (A)$\dfrac{2}{5}$
- (B)$\dfrac{59}{125}$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{64}{125}$
- (E)$\dfrac{3}{5}$
答案: B
习题19. (1995 AMC12 #20) 若$a,b,c$为从集合$\{1,2,3,4,5\}$中随机选取出的三个数字(可重复选取),试问$ab+c$为偶数的机率为何?
- (A)$\dfrac{2}{5}$
- (B)$\dfrac{59}{125}$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{64}{125}$
- (E)$\dfrac{3}{5}$
答案: B
习题20. (1996 AMC12 #22) 将一圆周平均分成1996段,所以有1996个平分点,今从此1996个点中选出4个不同的点$A,B,C,D$(每个点被取到的机率相同),则试求$\overline{AB}$弦与\overline{CD}$弦相交的机率为多少?
- (A)$\dfrac{1}{4}$
- (B)$\dfrac{1}{3}$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{2}{3}$
- (E)$\dfrac{3}{4}$
答案: B
习题21. (1996 AMC12 #26) 一箱子内有4种不同颜色的弹珠,分别为红、蓝、白、绿四色,今知每一次取出一个弹珠,取后不放回,连续取出4个,且下列四个事件发生的机率皆相同:
- (a) 取出四个红色
- (b) 取出一白三红
- (c) 取出一白、 一蓝、 二
- (d) 取出四个均不同色
则箱子中最少需要多少个弹珠, 才能满足上述条件?
- (A)$\dfrac{1}{4}$
- (B)$\dfrac{1}{3}$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{2}{3}$
- (E)$\dfrac{3}{4}$
答案: B
习题22. (1999 AMC12 #24) 已知在一圆上有6个点,任两点可形成一弦,从其中任取四弦,请问此四条弦可形成顶点在圆上之凸四边形的机率为多少?
- (A)$\dfrac{1}{15}$
- (B)$\dfrac{1}{91}$
- (C)$\dfrac{1}{273}$
- (D)$\dfrac{2}{455}$
- (E)$\dfrac{3}{1365}$
答案: B
习题23. (2000 AMC12 #23) Gamble教授买了一张乐透彩券,需从1到46个数字中选出六个数字填入,已知他所选之六个数字分别以10为底取log后,再加起来为一整数,若中奖之彩券也是依照此相同条件,则Gamble教授中奖的机率为多少?
- (A)$\dfrac{1}{5}$
- (B)$\dfrac{1}{4}$
- (C)$\dfrac{1}{3}$
- (D)$\dfrac{1}{2}$
- (E)$1$
答案: B
习题24.(2001 AMC12 #11) 一盒子中放有5个圆形筹码,其中3个是红色,2个是白色,每一次自盒子中任意取出1个筹码,取出后不再放回盒子中,直到所有红色或所有白色筹码被取出时为止,试求白色筹码先被取完的机率为多少?
- (A)$\dfrac{3}{10}$
- (B)$\dfrac{2}{5}$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{3}{5}$
- (E)$\dfrac{7}{10}$
答案: D
习题25.(2002 AMC12A #16) Tina从集合$\{1,2,3,4,5\}$随机选2个不同的数,Sergio从集合$\{1,2,...,10\}$随机选1个数,则Sergio选的数大于Tina选的2个数之和的机率为多少?
- (A)$\dfrac{2}{5}$
- (B)$\dfrac{9}{20}$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{11}{20}$
- (E)$\dfrac{24}{25}$
答案: A
习题26.(2004 AMC12B #4) 有一整数x,其中$10 \leq x \leq 99$,随机抽取出一个数字,且每一个数字被选择的机率相等,试求整数x的位数中至少有一个数字7的机率为何?
- (A)$\dfrac{1}{9}$
- (B)$\dfrac{1}{5}$
- (C)$\dfrac{19}{90}$
- (D)$\dfrac{2}{9}$
- (E)$\dfrac{1}{3}$
答案: B
习题27.(2005 AMC12B #11) 在一信封内有2张$1、2张$5、2张$10及2张$20,共8张钞票。由信封中以取后不放回的方式随机抽取出2张钞票,试问总金额大于或等于$20的机率为多少?
- (A)$\dfrac{1}{4}$
- (B)$\dfrac{2}{7}$
- (C)$\dfrac{3}{7}$
- (D)$\dfrac{1}{2}$
- (E)$\dfrac{2}{3}$
答案: D
习题28.(2006 AMC12A #22) 一个半径为$r$的圆,在其内部有一个边长为2的正六边形,且圆心与正六边形的中心重合。若站在圆上任一点可看见正六边形三个完整边的机率为$\dfrac{1}{2},试问r之值为何?
- (A)$2\sqrt{2} + 2\sqrt{3}$
- (B)$3\sqrt{3} + \sqrt{2}$
- (C)$2\sqrt{6} + \sqrt{3}$
- (D)$3\sqrt{2} + \sqrt{6}$
- (E)$6\sqrt{3} + \sqrt{3}$
答案: D
习题29. (2006 AMC12B #17) 有一对特殊的骰子,其各面点数$1,2,3,4,5$及$6$出现的机率比值为$1:2:3:4:5:6$,试问两颗骰子所投掷出来的点数和为$7$的机率为多少?
- (A)$\dfrac{4}{63}$
- (B)$\dfrac{1}{8}$
- (C)$\dfrac{8}{63}$
- (D)$\dfrac{1}{6}$
- (E)$\dfrac{2}{7}$
答案: C
习题30.(2007 AMC12A #12) 从$0$到$2007$中任意的选出整数$a,b,c,d$,它们不必都相异,试问$ad-bc$为偶数的机率是多少?
- (A)$\dfrac{3}{8}$
- (B)$\dfrac{7}{16}$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{9}{16}$
- (E)$\dfrac{5}{8}$
答案: E
条件机率
习题31. (1973 AMC12 #23) 有两张卡片,一张两面都是红的,另一张一面是红的一面是蓝的,两张卡片被选择的机率相等,皆为\dfrac{1}{2}。现在选择一张放在桌子上,试问该卡片上面一面是红的,则下面一面也是红的机率是多少?
- (A)$\dfrac{1}{4}$
- (B)$\dfrac{1}{3}$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{2}{3}$
- (E)$\dfrac{3}{4}$
答案: D
习题32. (1989 AMC12 #20) 设$x$为$100$到$200$之间任选的实数,若$\left[\sqrt{x}\right]=12$,则$\left[\sqrt{100x}\right]=120$的机率为多少?其中$\left[v\right]$是指不超过$v$的最大整数。
- (A)$\dfrac{2}{25}$
- (B)$\dfrac{241}{2500}$
- (C)$\dfrac{1}{10}$
- (D)$\dfrac{96}{625}$
- (E)$1$
答案: B
习题33. (2003 AMC12B #19) 设$S$为数列$1,2,3,4,5$的所有排列中,第一个数字不可为$1$的排列所形成的集合。令最简分数$\dfrac{a}{b}表示从集合$S$中随机挑选出一种排列,其第二个数字为$2$的机率,试求$a+b$之值为何?
- (A)$5$
- (B)$6$
- (C)$11$
- (D)$16$
- (E)$19$
答案: E
几何机率
习题34. (1987 AMC12 #26) 将$2.5$随机地分解成两个非负实数的和,例如$2.5=2.143+0.357$或$2.5=\sqrt{3}+(2.5-\sqrt{3})$。再把每一数改为与它最接近的整数,如前面第一个例子的$2.143,0.357$分别改为$2,0$,而第二个例子的$\sqrt{3,(2.5-\sqrt{3})}$分别改为$2,1$,试问在这样的规则下最后得到的两整数和为$3$的机率是多少?
- (A)$\dfrac{1}{4}$
- (B)$\dfrac{2}{5}$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{3}{5}$
- (E)$\dfrac{3}{4}$
答案:B
习题35.(2003 AMC12A #16) 在正三角形$ABC$内部中任取一点$P$,则$\triangle ABP$的面积同时大于$\triangle ACP$与$\triangle BCP$面积的机率为何?
- (A)$\dfrac{1}{6}$
- (B)$\dfrac{1}{4}$
- (C)$\dfrac{1}{3}$
- (D)$\dfrac{1}{2}$
- (E)$\dfrac{2}{3}$
答案:C
习题36.(2003 AMC12B #21) 有一物体由$A$点直线前进$8$公分至$B$点,再转$\alpha$弧度至另一方向,其中$\alpha \in (0, π)$,之后再直线前进$5$公分至$C$点,试求$\overline{AC}>7$的机率为何?
- (A)$\dfrac{1}{6}$
- (B)$\dfrac{1}{5}$
- (C)$\dfrac{1}{4}$
- (D)$\dfrac{1}{3}$
- (E)$\dfrac{1}{2}$
答案:D
习题37.(2003 AMC12B #25) 由一圆的圆周上任取三点,试求在此三点中,任意两点间的距离皆会小于圆半径的机率为何?
- (A)$\dfrac{1}{36}$
- (B)$\dfrac{1}{24}$
- (C)$\dfrac{1}{18}$
- (D)$\dfrac{1}{12}$
- (E)$\dfrac{1}{9}$
答案:D
习题38.(2004 AMC12A #20) 从0与1之间随机独立的取出两实数a与b,并将a,b之和记作c,分别以A,B,C表示最接近a,b,c的整数,试问A+B=C的机率为多少?
- (A)$\dfrac{1}{4}$
- (B)$\dfrac{1}{3}$
- (C)$\dfrac{1}{2}$
- (D)$\dfrac{2}{3}$
- (E)$\dfrac{3}{4}$
答案:E
习题39.(2006 AMC12B #20) 令x为由区间(0,1)中随机挑选的数,试求满足下列方程式
之机率为多少?其中$\left[x\right]$表示小于或等于$x$的最大整数。
- (A)$\dfrac{1}{8}$
- (B)$\dfrac{3}{20}$
- (C)$\dfrac{1}{6}$
- (D)$\dfrac{1}{5}$
- (E)$\dfrac{1}{4}$
答案:C
习题40.(2008 AMC12B #21) 平面上有两个半径为$1$的圆$A,B,$其中圆$A$的圆心为$(0,0)$到$(2,0)$所形成的线段中随机挑选,而圆B的圆心为$(0,1)$到$(2,1)$所形成的线段中随机挑选,试问圆$A$与圆$B$相交的机率为多少?
- (A)$\dfrac{2+\sqrt{2}}{4}$
- (B)$\dfrac{3\sqrt{3}+2}{8}$
- (C)$\dfrac{2\sqrt{2}-1}{2}$
- (D)$\dfrac{2+\sqrt{3}}{4}$
- (E)$\dfrac{4\sqrt{3}-3}{4}$
答案:E
路径问题
习题41.(2003 AMC12A #22) 两物体$A$与$B$经由一系列步骤同时等速在座标平面上移动,每次移动一个单位。物体$A$从$(0,0)$开始移动,且每一步骤是向右或向上,两者机率一样。物体$B$从$(5,7)$开始移动且每一步骤是向左或向下,两者机率一样,则两物体$A$与$B$相遇的机率约为多少呢?(四捨五入到小数点第二位)
- (A)$0.01$
- (B)$0.15$
- (C)$0.20$
- (D)$0.25$
- (E)$0.30$
答案:C
习题42.(2005 AMC12B #25) 有六只蚂蚁同时站在正八面体的相异六个顶点上,然后这六只蚂蚁同时且独立的移动至与其原本所站之顶点相邻的四个顶点之一,移动至每一个顶点的机率皆相同,试求没有任何两只蚂蚁会在同一个顶点相遇的机率为多少?
- (A)$\dfrac{5}{256}$
- (B)$\dfrac{21}{1024}$
- (C)$\dfrac{11}{512}$
- (D)$\dfrac{23}{1024}$
- (E)$\dfrac{3}{128}$
答案:A
习题43.(2009 AMC12B #17) 在立方体的每一个面上,选择某一边的中点画一条线至另一边的中点,而在每一面上随机且独立的选择一双对边,试问会有一连续的线环绕立方体的机率为何?
- (A)$\dfrac{1}{8}$
- (B)$\dfrac{3}{16}$
- (C)$\dfrac{1}{4}$
- (D)$\dfrac{3}{8}$
- (E)$\dfrac{1}{2}$
答案:B
附录: 本附录按年份列出所收集的全部AMC12之机率题目,题号栏第一个数字为该年AMC12之题号,括号内第一个数字为此题在本文之题号,第二个数字为所在页数。如:196336(35,24)表示此题为1963年AMC12第36题考题,在本文所在位置为第35题、第24页;200713B(27,16)表示此题为2007年AMC12之B卷第13题考题,在本文所在位置为第27题、第16页
| 年份 | 题号 |
|---|---|
| 1963 | 36 (10, 75) |
| 1970 | 31 (11, 75) |
| 1971 | 23 (140期 9, 69) |
| 1972 | 17 (1, 64) |
| 1973 | 23 (31, 79) |
| 1974 | 24 (140期 15, 72) |
| 1975 | 18 (140期 18, 75) |
| 1976 | 8 (140期 3, 66) |
| 1977 | 17 (140期 4, 66) |
| 1978 | 19 (140期 2, 65) |
| 1979 | 27 (140期 11, 70) |
| 1980 | 20 (140期 12, 70) |
| 1981 | 26 (12, 75) |
| 1982 | 25 (8, 72) |
| 1975 | 18 (140期 18, 75) |
| 1976 | 8 (140期 3, 66) |
| 1977 | 17 (140期 4, 66) |
| 1978 | 19 (140期 2, 65) |
| 1979 | 27 (140期 11, 70) |
| 1980 | 20 (140期 12, 70) |
| 1981 | 26 (12, 75) |
| 1982 | 25 (8, 72) |
| 1983 | 15 (140期 22, 77), 26 (140期 17, 74) |
| 1984 | 19 (13, 75) |
| 1985 | 6 (140期 1, 65), 24 (140期 19, 75) |
| 1986 | 22 (140期 8, 68) |
| 1987 | 26 (34, 79) |
| 1988 | 12 (140期 13, 71), 28 (14, 75) |
| 1989 | 20 (32, 79) |
| 1990 | 18 (15, 76) |
| 1991 | 13 (16, 76) |
| 1992 | 29 (17, 76) |
| 1993 | 24 (140期 6, 67) |
| 1994 | 27 (140期 25, 81), 30 (18, 76) |
| 1995 | 20 (19, 76) |
| 1996 | 16 (140期 21, 77), 22 (20, 76), 26 (21, 77) |
| 1997 | 10 (140期 10, 69) |
| 1999 | 24 (22, 77), 29 (7, 70) |
| 2000 | 23 (23, 77) |
| 2001 | 11 (24, 77), 17 (4, 66) |
| 2002 | 16A (25, 77), 16B (140期 16, 74), 18B (5, 67), 15C (140期 23, 78) |
| 2003 | 8A (140期 5, 66), 16A (35, 79), 22A (41, 81), 19B (33, 79), 21B (36, 80), 25B (37, 80) |
| 2004 | 20A (38, 80), 4B (26, 78), 20B (140期 14, 72) |
| 2005 | 14A (140期 24, 80), 23A (140期 20, 76), 11B (27, 78), 25B (42, 81) |
| 2006 | 20A (9, 73), 22A (28, 78), 17B (29, 78), 20B (39, 80) |
| 2007 | 12A (30, 78), 13B (2, 65) |
| 2008 | 21B (40, 80), 22B (140期 7, 67) |
| 2009 | 17B (43, 81), 18B (3, 65), 23B (6, 68) |
- 1. Artino, R. A., Gaglione, A. M. and Shell, N. (1982). Contest Problem Book IV: Annual High School Examinations 1973~1982. Washington, DC: The Mathematical Association of America.
- 2. Berzsenyi, G. and Maurer, S. B. (1997). Contest Problem Book V: American High School Mathematics Examinations and American Invitational Mathematics Examinations 1983~1988. Washington, DC: The Mathematical Association of America.
- 3. Maurer, S. B., Reiter, H.B. and Schneider, L. J. (2001). The American High School Mathematics Examination: A 50 year Retrospective. Mathematics Competitions 14, 45-66.http://www.math.uncc.edu/~hbreiter/AHSME/Steve&Leo.html
- 4. Reiter, H. B. (2006). The Contest Problem Book VII: American Mathematics Competitions, 1995~2000 Contests. Washington, DC: The Mathematical Association of America.
- 5. Rusczyk, R. et al. “Art of Problem Solving Forum.” From AoPS Incorporated.http://www.artofproblemsolving.com/Forum/resources.php?c=182&cid=44
- 6. Salkind, C. T. (1961). Contest Problem Book: Problems from the Annual High School Contests of the Mathematical Association of America. New York: Random House.
- 7. Salkind, C. T. (1966). Contest Problem Book II: Annual High School Contests 1961~1965. Washington, DC: The Mathematical Association of America.
- 8. Salkind, C. T. and Earl, J. M. (1973). Contest Problem Book III: Annual High School Contests 1966~1972. Washington, DC: The Mathematical Association of America.
- 9. Schneider, L. J. (1997). Contest Problem Book VI: American High School Mathematics Examinations and American Invitational Mathematics Examinations 1989~1994. Washington, DC: The Mathematical Association of America.
- 10. Wells, D. and Faires, J. D. (2008). The Contest Problem Book IX: American Mathematics Competitions (AMC12) 2001~2007. Washington, DC: The Mathematical Association of America.
- 11. 财团法人九九文教基金会。 http://www.99cef.org.tw/




