有风险的业务:怎样对衍生工具定价

在全球商业中,公司希望消除尽可能多的风险。做到这一点的方法之一是通过购买称为衍生工具的金融产品。这些产品可以被认为是保险的政策:如果一家公司购买这些衍生产品之一,他们可以确保他们在未来不承受一定的风险。这些衍生工具自己也可以进行交易;事实上,这个交易既有可能赚大钱,也有可能输掉钱。
作为衍生工具的一个例子,考虑航空公司今天销售一张在一年时间内有效的机票。燃料是航空公司最大的成本之一,因此它不希望发现客户支付的价格甚至抵消不了一年之内的燃料成本。避免这种风险的一个好方法是航空公司签订一个远期合同,这是一种衍生金融工具,其中规定航空公司在一年的时间里将支付的燃料价格。当然,燃料价格可能有机会下降,在这种情况下,在远期合同中约定的价格可能要比航空公司等了一年后购买的燃料价格高得多。然而,大多数公司更喜欢摆脱尽可能多的风险,这就解释了为什么衍生工具对他们非常有用。
期权
当然,如果银行销售衍生工具,必须知道应该卖它多少钱,这就用到数学家了。假设有一个资产,其价格在未来是未知的。我们把这个资产称为股票(又称股),虽然我们目前的分析对其他资产也有效。我们将假设该资产不会产生任何股息,也就是说,除了持有资产我们不获得任何其他收益。(这是一种简化,但它使分析更为简单,如果我们愿意的话,我们也可以处理股息)。衍生工具则是一种资产,其价格取决于相关股票的行为。在这篇文章中,我们将着眼于称为欧式看涨期权的一种衍生工具。这是一种契约,它赋予持有人有权(但无义务)在未来一个固定 的时间,以固定价格买一只股票。更具体地说,欧洲看涨期权指定一个终止时间$T$,加上行权价$K$。欧式看涨期权的持有人有权在时间$T$以价格$K$购买股票。当然,如果$K$小于市场价格,持有人将只买股票。因此,如果在时间$T$的股票价格为$S_T$,则欧式看涨期权的回报为
一个欧式看涨期权是一种类型的期权,这样命名是因为其持有人有执行或不执行的选择。
期权定价:一个简单的模型

有一个简单的模型,被称为二项式模式,这给我们提供了一种期权定价。它和布莱克-斯科尔斯(Black-Scholes)模型基于相同的基本想法,后者是金融数学的心脏,为此迈伦·斯科尔斯和罗伯特·默顿获得了1997年的诺贝尔经济学奖(费希尔·布莱克在该诺贝尔奖之前两年去世)。
我们假设只有两种资产:债券,股票。债券为无风险资产,这意味着我们现在已经知道它在下一时间步的价值。你可以把该债券看成一个银行帐户。另一方面,股票是有风险的资产,意指我们事先不知道它的价值。
我们首先看一个时间段。在开始的时候(时间0),债券价格为1,股票价格为$S_0$。在期间结束时(时间$T$)债券价格将是$1 + r$,其中$r$是这段时间$T$所收取的利息。相反,在这个简化模型中,风险资产可以采取两种可能的值之一:如果这期间表现好,那么价格将以一个因子$u$增加,因此股票价格将上涨至$S_0u$,而如果是坏的时期,价格会以因子$d$变差,这样股票价格将减少至$S_0d$。我们 假设好时期的概率是$p$,但我们会在后面(显著)可见,这个概率与期权定价的计算是不相关的。
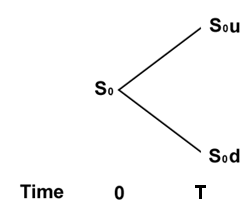
在这个模型中,一个人可以随意持有他们(正或负)的股票或债券。我们还要求条件
如果第一个不等式不成立,即如果$d > 1 + r$,那么每个人都借钱(即购买的债券金额为负数),并用这笔钱购买股票。该时间段结束时,股票的价值,即使它的表现不佳,将超过所欠的债券。这一战略将保证给予了肯定的无风险利润。类似的无风险战略在$u 套利,自然我们要从我们的模型中排除这样的套利机会。
我们现在考虑期权,如果股价上涨则有回报$y_u$,而如果股票下跌则有$y_d$。我们愿意出多少钱支付这个期权?原来,有一个特定价格,因为我们可以精确地复制期权的回报。
假设时间为零时,我们买$x$单位的债券并投资金额为$z$的股票。在时间$T$时,我们持有的债券价值为$x(1+r)$,持有的股票价值如果股价上涨为$zu$,否则则为$zd$。我们可以任意选择$x$和$z$。特别,我们可以选择它们使得
如果我们选择这样的$x$和$z$,那么我们的股票和债券的价值在第一期结束时与期权完全一样。我们在时间0时可以支付金额$x + z$,在第一阶段结束时,我们收到完全与期权匹配的回报。复制期权回报的股票和债券投资组合被称为{\bf 复制组合}。时间为零时期权的值必须是$x + z$,因为如果以任何其他值交易的话,那么在我们的模型中将有两个实体(复制组合和期权)有相同的回报,但成本却不同。如果发生这种情况,每个人都会买一个而卖其他以获取无风险的利润。因此,$x + z$是期权价格。
我们可以求解上述两个联立方程,得到
现在,期权的价格由
给出。为了让事情看起来更简单,我们定义
则我们就可以将期权价格表达为
等价概率
比较奇怪的是,好时期的概率$p$在此公式中不起任何作用。如果你熟悉概率论,那么你可能会认为由下式某种平均
给出的期权回报的预期值应该会出现在期权价格的公式中。类似的表达式确实出现,但$p$由$q$代替,然而$q$只取决于利率$r$和可能出现的股票价格变化$u$和$d$。量$q$和$1-q$因此被称为等价概率。值得注意的是,等价概率足以确定期权价格:真正的向上或向下跳变的概率是无关紧要的。
通向布莱克-斯科尔斯之路
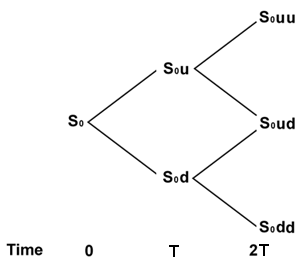
我们的模型只持续一个时间段,我们想将其扩展到多期间的情形。因此,让我们假设现在有两个时期,长度都是$T$。在每个时期的股票可以上涨或下跌,如右图所示。现在股票价值有三种可能的结果($S_0 uu, \; S_0 du$或$S_0 dd$)。我们假设该期权在第二阶段结束时到期,我们让$y_{uu}, \; y_{uu},\; y_{dd}$分别表示期权三种结果之一的值。
为了给这个期权定价,首先假设在第一时期段内,股价上升。现在考虑我们应该持有多少股票和债券,以复制期权到期时的回报。从上述的单期模型中我们知道,如果我们投资组合的股票和债券在到期时价值正好为$y_{uu}$或$y_{ud}$,则在第二个期间段开始时它必须值
同样,如果股票在第一时期内下跌,则在第二时期开始时我们的投资组合应该值
运用我们的单期模型,我们可以看到一个投资组合要在第一时期之后实现值$Y_u$和$Y_d$,在零时刻它要值
将$Y_u$和$Y_d$的值带入,我们得到
这是复制投资组合的价格,因此也是期权的价格。
使用同样的想法,可以将这个模型扩展到三、四、五或任何数量的时间段。事实上,使用一些数学符号,可以写出有$n$个时期的通式
此公式中的符号在这里解释,但不要过分担心公式本身。重要的一点是,我们期限届满向后分析的技术对任何数目的时期都工作。勇敢的读者可以尝试用数学归纳法证明这一点。
极限下的布莱克-斯科尔斯

二项式模型对理解期权定价背后的想法而言是一个非常简单的模型。然而,到目前为止,股价只能取有限多个值,而且只能在离散的时间点移动。这两个特点是有些不受欢迎的,但有一个聪明的办法解决这个问题。其基本思想是将期权期满的时间分成$n$个大小相等的时间段,看看当$n$趋向于无穷大,即当各小时间段趋向于零时,在此极限情形模型会发生什么。这将我们的模型从离散时间推进到连续时间。
实际操作的数学是有点太多(但是有兴趣的读者可以从附录中看到它)。事实上,没有必要去追究它:重要的一点是,我们的简单模型可以变成一个关于期权定价的单一精确表达式。这就是金融数学著名的布莱克-斯科尔斯方程。它所依赖的仅有参数是履约价格$K$、到期时间$T$、目前股价$S_0$、利率$r$和所谓的波动。最后这个参数描述股票价格的可变性,并具有精确的数学定义。
来自我们推导的重要信息与其说是结果所得到的公式(在右边),还不如说是以何种方式得到了它。我们看到在离散时间模型中,我们如何能够通过选择正确数量的股票和债券而准确地复制期权回报。这就告诉我们,时间为0时的期权价格应当等于复制期权的成本。连续时间的基本思想是完全一样的:我们应该选择我们的股票和债券,使得它们完全匹配期权到期后的回报。当然,由于我们着眼于连续时间,持有的股票和债券金额需要连续调整,而不是以离散时间的方式。然而,复制的想法是完全一样的。
其他期权

布莱克和斯科尔斯在1973年撰写的论文,使用复制的想法决定欧式看涨期权的价格,但他们的做法与这里介绍的有点不同。他们直接从一个连续时间模型开始,其中股票价格是一个布朗运动的函数:布朗运动是与你所看到的粒子漂浮在液体或气体中的随机运动相类似的。在数学上,布朗运动是一个随机过程,满足一定的性质。布莱克和斯科尔斯的论文展示了如何可以将期权定价转化为求解给定某些边界条件的偏微分方程问题。事实上,他们能够转换这些偏微分方程,并证明他们等价于求解物理学中的热传导方程。不幸的是,看到与偏微分方程理论之间的联系所需要的数学要用到随机微积分,这需要相当的努力才能建立其机制。
虽然我们只展示了如何定价欧式看涨期权,我们可以使用相同的分析,对其回报只取决于期间终端股票价值的任何期权定价。 布莱克-斯科尔斯的理论确实很一般。然而,也有很多其他各种各样的期权,不属于该理论的适用范围。 为这样的奇异期权定价创造了许多有趣的数学问题,并让金融数学家闲不下来。




