神奇的Gamma函数 (中)
Gamma 函数欣赏
Each generation has found something of interest to say about the gamma function. Perhaps the next generation will also.
—Philip J.Davis
Gamma 函数从它诞生开始就被许多数学家进行研究，包括高斯、勒让德、威尔斯特拉斯、柳维尔等等。这个函数在现代数学分析中被深入研究，在概率论中也是无处不在，很多统计分布都和这个函数相关。Gamma 函数作为阶乘的推广，首先它也有和 Stirling 公式类似的一个结论
另外， Gamma 函数不仅可以定义在实数集上，还可以延拓到整个复平面上。
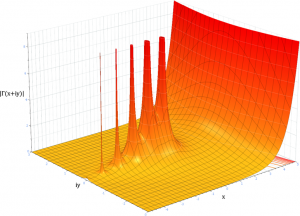复平面上的Gamma 函数
| frist derivative | $nx^{n-1}$， |
| second derivative | $n(n-1)x^{n-2}$， |
| third derivative | $n(n-1(n-2)x^{n-3}$， |
| $\cdots$ | |
| k-th derivative | $n(n-1(n-2)\cdots(n-k+1)x^{n-k}=\dfrac{n!}{(n-k)!}x^{n-k}$， |
由于k阶导数可以用阶乘表达，于是我们用Gamma 函数表达为
于是基于上式，我们可以把导数的阶从整数延拓到实数集。例如，取$n=1, k=\frac{1}{2}$我们可以计算 $x$ 的 $\frac{1}{2}$阶导数为
很容易想到对于一般的函数 $f(x)$ 通过 Taylor 级数展开可以表达为幂级数，于是借用 $x^n$ 的分数阶导数，我们可以尝试定义出任意函数的分数阶导数。不过有点遗憾的是这种定义方法并非良定义的，不是对所有函数都适用，但是这个思想却是被数学家广泛采纳了，并由此发展了数学分析中的一个研究课题：Fractional Calculus,在这种微积分中，分数阶的导数和积分都具有良定义，而这都依赖于 Gamma 函数。
Gamma 函数和欧拉常数$\gamma$ 有密切关系，可以发现
进一步还可以发现 Gamma 函数和黎曼函数$\zeta(s)$有密切联系，
而$\zeta$ 函数涉及了数学中著名的黎曼猜想和素数的分布定理。希尔伯特曾说，如果他在沉睡1000年后醒来,他将问的第一个问题便是:黎曼猜想得到证明了吗？
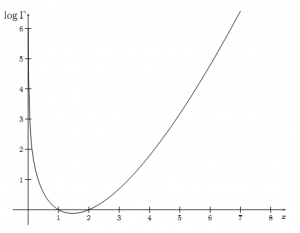$\log \Gamma(x)$
从Gamma 函数的图像我们可以看到它是一个凸函数, 不仅如此, $\log\Gamma(x)$ 也是一个凸函数，数学上可以证明如下定理:
[Bohr-Mullerup定理] 如果 $f:(0,\infty)\rightarrow (0,\infty)$,且满足
$f(1) = 1$
$f(x+1) = xf(x)$
$\log f(x)$ 是凸函数
那么 $f(x) = \Gamma(x)$, 也就是 $\Gamma(x)$是唯一满足以上条件的函数。
如下函数被称为 Digamma 函数，
这也是一个很重要的函数，在涉及求Dirichlet 分布相关的参数的极大似然估计时，往往需要使用到这个函数。Digamma 函数具有如下一个漂亮的性质
函数$\Psi(x)$和欧拉常数$\gamma$ 以及 $\zeta$ 函数都有密切关系，令
$$\Psi_n(x) = \frac{d^{n+1}\log\Gamma(x)}{dx^{n+1}}$$
则 $\Psi_0(x) = \Psi(x)$,可以证明
所以Gamma 函数在数学上是很有魅力的，它在数学上应用广泛，不仅能够被一个理科本科生很好的理解，本身又足够的深刻，具有很多漂亮的数学性质，历史上吸引了众多一流的数学家对它进行研究。美国数学家 Philip J.Davis 写了篇很有名的介绍 Gamma 函数的文章：“Leonhard Euler’s Integral:A Historical Profile of the Gamma Function”，文中对 Gamma 函数一些特性发现的历史进行了很详细的描述，这篇文章获得了 Chauvenet Prize(美国数学会颁发的数学科普最高奖)。
