薛定谔方程在行动
假设你有一个粒子在一个盒子内的两堵墙之间来回反弹，且粒子只沿着一维的$x$-轴，在两个不能穿过的垂直墙$x = 0$和$x = L$之间运动。在盒子内部没有力作用在粒子上，所以这里它的势能为0，即对$0
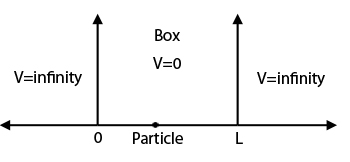盒子中的粒子 因为在这个例子中势能不依赖于时间，在盒子内我们可以使用不依赖于时间的一维薛定谔方程：
$$ \frac{d^2\psi}{dx^2} + \frac{8 \pi^2 m E \psi}{h^2} = 0, \hspace{1in} (1) $$其中$m$为粒子的质量，$E$是它的 总能量，$h=6.626068 \times 10^{-34}m^2 kg/s$是普朗克常数。
方程(1)的解是一个函数$\psi(x)$，具有下面的一般形式
其中$A$与$B$为任意常数。
当时间为$t$时，在位置$x$处粒子的概率和$|\psi(x)|^2$有关。我们知道，因为粒子需要无穷大的能量才能冲出盒子外（即 到达$x L$的区域），所以它不可能离开盒子。这意味着当$x L$时，$\psi(x) = 0$。因为 $\psi$在盒子的边界处是连续的，我们得到$\psi$在$x = 0$和$x = L$时也为$0$。
第一个边界条件$\psi(0) = 0$意味着
因此我们可以丢掉第一项，这样我们的方程变为
而第二个边界条件$\psi(L) = 0$意味着
因而或者$B = 0$或者正弦项为 $0$。前者推出$\psi$处处为$0$，但这是不可能的，因为我们知道粒子总在盒子的某处。这样我们得到
因为$\sin y = 0$当且仅当$y$是 $\pi$的倍数，因此
换言之，
其中$n$为一正整数。这告诉我们粒子的能量只能是 对应于$n = 0, 1, 2, \ldots$的离散值
对应于能量级$E_n$的$n$称为$E_n$的量子数 。
量子数$n = 0$对应于零能量---但它也给出在盒子里处处为零的波函数$\psi_0$，意味着粒子不能位于盒子中的任何地方。这 样，量子数$n = 0$也要出局，结果是被允许的能量级为
波粒二象性是量子力学中的核
心概念。 能量谱是离散的，即并不是所有的能量都被允许（特别是零能量不能出现），这一结果是无法从经典力学中得到的结果。事实 上，它挑战了像能量这样的量应该连续变化的传统智慧：根据莱布尼茨的说法，“自然不让跳跃”。经典物理也告诉我们，一个 系统的最低能量状态（也称为真空基态）应当具有零能量。但是这些奇怪的量子结果与量子系统的实验观察相吻合，例如氢原子 的离散能量谱。
进一步地，我们知道常数$B$的值可以通过对波函数归一化而获得。回想$|\Psi(x)|^2$是于时刻$t$在位置$x$处发现粒子的概 率密度，并且有下面的关系：
其中$e^ {- (2\pi E/h)t}$是一个复数，可以写成
根据三角函数中的恒等 式，
复数的模$|e^{- (2\pi E/h)t}|$为$1$ 。因此有
因此，粒子在盒子中某处的概 率由式子
给出。因为知道粒子总是在盒子的某一处 ，就有
把$\psi(x)$的表达式(3)带入，就得 到
利用下面的 不定积分：
我们计算出
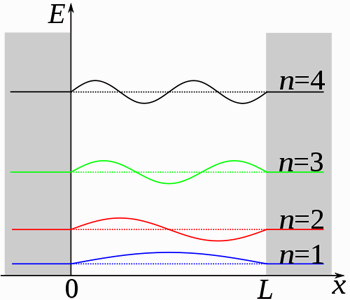盒子中的粒子：x轴表示粒子的
位置，y轴表示粒子的能量。允许的前4级能量水平在图中用水平虚线表示。波函数叠加显示在图中相应的能量水平位置上。图片来源：Papa November
因此我们最后推导出：
将 (4)式给出的$E$的可能值$E_n$带入，我们有无穷个波函数$\psi_n(x)$（每个量子数，即允许的能量级，与之一一对应）：
这给了又一个令人惊讶的结果：对大于$1$的任何$n$，我们都可以找到盒子中的一点$x$使得$\psi_n(x) = 0$，说 得更明白一点，取$x = kL /n$，其中整数$k
因为$|\psi(x)|^2 = |\Psi(x)|^2$是在位置$x$处发现粒子的概率密度，这意味着在盒子中有个位置在那里永远找不到粒子！
这样我们看到了薛定谔方程如何产生了与经典直观相冲突的一个奇怪的结果。那么为什么在像桌球这样的宏观物体中看不到 离散的能量级？我们试图解释如下：最小能量在量子数$n = 1$处出现，这时
注意到普朗克常数$h$非常小：$h=6.626068 \times 10^{-34}m^2 kg/s$，故对大的物体，出现在分母的$m$和$L$相对很大。这意味着$E_1$是非常非常的小，以至于一个具有能量$E_1$的物体与处 于静止状态的物体几乎没有区别。这就是为什么在宏观世界零能量级确实是可能的。
现在我们对某个量子数$n$来计算两个相近能量级$E_n$与$E_{n+1}$之间的差：
当质量$m$和尺寸$L$变得很大后，这个差趋向于$0$。因此对于大的物体，可允许的能量级之间的距离可以非常小 ，以至于无法将它们与不被允许的能量级区分开来，这也会导致能量级看上去在连续变化。
量子隧道
现在让我们把设置改变一点点。我们依然假设粒子沿着$x$-轴运动，但这次设想势能$V$对$-\infty
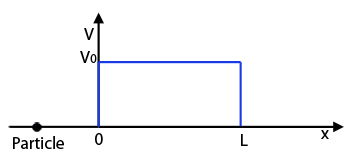量子隧道：纵坐标表示粒子势
能，当x大于0，小于L的时候粒子势能等于$v_0$,其他位置势能都为零. 这就像一个滚动着的质量为$m$的球遇到一座高度为$H$的山坡：假如它有足够大的能量滚动到山顶，那么它在那里的势能将是 $V_0 = m g H$，其中$g$是引力加速度。如果它的能量小于$V_0$，则它永远到达不了山顶。在我们的例子中山坡的斜率是垂直的 ，因为在$x = 0$和$x = L$势能不连续地从$0$跳跃到$V_0$。它在顶端是水平的，因为势能$V$在$0
但在量子力学里，即使它的能量小于$V_0$，粒子仍可以到达顶部，甚至还可以爬到“势垒”的另一边。由于篇幅的原因，我 们不在此细说这件事情的原因，但我们指出：求解$E
通常，量子隧道这一术语指的是一个粒子克服势垒的任何情形，而根据经典物理学它则克服不了。在自然中量子隧道确实能出 现，例如在镭衰变为钍的过程中以一种名为$\alpha$-衰变的放射性衰变的形式出现。这里原子核放射出$\alpha$-粒子，它由两 个质子和两个中子组成，和氦原子核的结构相同。而在经典物理学中，释放粒子的过程应当是不可能的，因为它需要比原子所具 有的更大的能量。
