[题图是 John Landen 的文集第一卷的扉页。]

我们现在要暂时离开 Gauss，回到 Euler 与 Fagnano 以及二次曲线上来。

我们在这一系列的预篇中提到，Euler 在 1752 年 2 月 1 日，也就是在他的论文宣读不久以后，就写信给Pierre Louis Maupertuis。他在信中提到了自己几天前宣读的论文 [原文来自 Correspondance de Leonhard Euler avec P.-L. M. de Maupertuis et Frederic II，194 页]：

...Jeudy passé j'ai lu une piece sur la comparaison des arcs des courbes Lemniscate, Ellipsis et hyperbole, à la quelle m'a donné occasion le livre de Fagnani, et je crois avoir decouvert des methodes asses remarquables sur cette matiere. Par exemple cette proprieté de l'Ellipse m'a fort frappé. ...……上周四 [注：1752 年 1 月 27 日] 我宣读了一篇关于双纽线，椭圆以及双曲线弧长的文章，这篇文章 [产生的契机] 是 Fagnano 的书，我从这里 [指曲线弧长的研究] 中发现了引人注目的方法。譬如说下面这个关于椭圆的性质就给我以很深的印象。……

Fagnano 文集第二卷中紧挨着双纽线弧长的相关文章题名为Teorema da cui si deduce una nuova misura degli archi elittici, iperbolici, e cicloidali[关于椭圆，双曲线，摆线弧长的新定理]，发表于 1716 年。这篇文章开篇提出的定理是这样的：

定理：设$f,g,h,l$为常数。并且设    $$\begin {align} X=\sqrt {\frac {hx^2+l}{fx^2+g}}\mathrm {d} x\\Z=\sqrt {\frac {hz^2+l}{fz^2+g}}\mathrm {d} z\end {align}$$    如果$fhx^2z^2+flx^2+flz^2+gl=0$, 那么就有$X+Z=-\frac {h}{\sqrt {-lf}}\mathrm {d}(xz)$。

这个定理的证明是非常直白的。那么，它和 Fagnano 文章的标题有什么关系呢？

Euler 对Fagnano 命题的几何解释

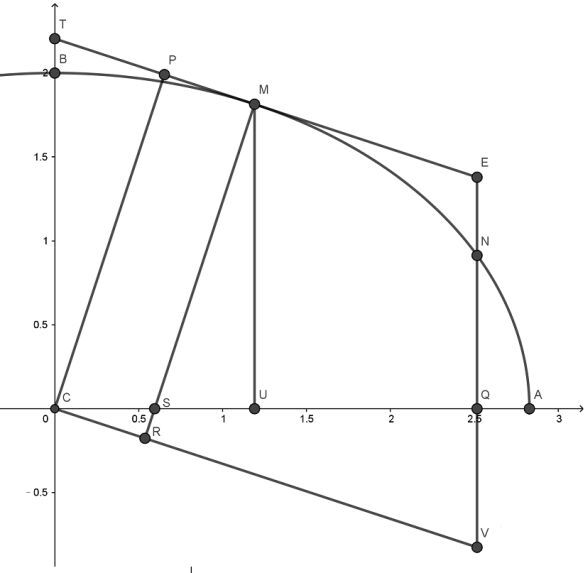
假设图中的椭圆长半轴为 1，短半轴为 c，长半轴端点为 A，中心为 C，短半轴端点为 B。若椭圆上的点 M 的横坐标为 CU=x，那么椭圆的弧长微分为$\sqrt {\frac {1-nx^2}{1-x^2}}\mathrm {d} x$，其中$n=1-c^2$。如果我们令 Fagnano 定理中的$g,l=1$,$f=-1$,$h=-n$，那么 Fagnano 的命题变为：如果$nx^2z^2-x^2-z^2+1=0$，那么$X+Z=n\mathrm {d}(xz)$。设椭圆上横坐标为 z 的点为 N，CQ=z，那么，结论可以改造为弧 BM-弧 AN=nxz(为什么？)。也就是说，椭圆上可以找到两段弧，使得其弧长的差值可以用弧长始末端点的坐标的代数函数表示。

Euler 在 1752 年的论文给等式右面的量$nxz$找了一个漂亮的几何解释。过点 M 作 M 关于椭圆的法线，用解析几何的结论可知法线在 x 轴上的截距 CS=nx。那么$nxz=CS\cdot CQ$。过 C 作 MS 的垂线，与 MS 交于 R，与 NQ 交于 V。那么 CV=CA=1 (为什么？)。所以$nxz=CS\cdot CQ=CR\cdot CV=CR$。我们就得到 Euler 的结论：

过 M 作椭圆的切线。设 CP 是 C 到切线的垂线，P 是垂足。MP 交 y 轴于 T。E 在 MP 上，且 TE=CA。过 E 作 BC 的平行线交椭圆于 N。那么弧 BM-线段 MP = 弧 AN. 这正是 Euler 在信中描述的 "关于椭圆的性质"。这一性质引起 Euler 的重视不是没有道理的。Euler 研究中的某一步推理是 20 多年后一项重要工作的重要前提，而这项工作是 Euler 生前完全不知道的。

John Landen,F. R. S.(1719-1790) 和 Fagnano 一样，都是只因为一项研究而留名于世的数学研究者。Landen 的主业是贵族的地产经纪人。他在 1780 年和 1790 年发表了他的两卷数学论文集。在编纂第二卷论文时 Landen 已经身患重病，拿到刚出版的第二卷论文集的次日就去世了。他的两卷文集中只有一篇文章是纯粹数学的文章，其他都是数学物理相关的内容。这唯一的一篇纯粹数学文章题名即为Of the Ellipsis and Hyperbola, 汇集了他 1771 年和 1775 年发表在英国皇家学会的刊物Philosophical Transactions两篇文章的主要内容。Landen 的发现被 Lagrange 和 Legendre 变成了椭圆积分计算的利器，Landen 也因此成了欧洲大陆 (至少是法国) 数学家口中英国分析学家的代表之一。

Landen 本人应当很看重自己的关于椭圆和双曲线的研究。他在文集第一卷的序言中特地提到：

But I almost assure myself, there are few geometricians who will not be pleased with the discovery of the theorem in the second Memoir, which enables us toassign the length of any arc of any conic hyperbola by means of two elliptic arcs——a thing which, I am inclined to believe, had not even been thought possible by former writers on the properties of those curves; and of whose use there are many remarkable instances in the following pages.

说实话，Landen 所使用的符号实在是令人生厌。我们就绕开他的这些符号，直击他的文章的核心部分。我们仍然继承上图中的所有记号，并且记 MP=u。我们已经知道，$u=nxz=nx\sqrt {\frac {1-x^2}{1-nx^2}}$，而且椭圆的弧长微分$ds=\sqrt {\frac {1-nx^2}{1-x^2}}\mathrm {d} x$。那么，我们就有$\mathrm {d} s=\frac {nx}{u}\mathrm {d} x$。解关于$x$的方程，$u=nx\sqrt {\frac {1-x^2}{1-nx^2}}$，我们有

$$x^2=\frac {1}{2n}\left (u^2+n-\sqrt {(u^2+n)^2-4u^2}\right)$$

在等式两侧微分，化简后我们就有

$$\mathrm {d} s=\frac {nx}{u}\mathrm {d} x=\frac {1}{2}\left (1+\frac {2-u^2-n}{\sqrt {(u^2+n)^2-4u^2}}\right)\mathrm {d} u.$$

将$n=1-c^2$代回，就有

$$(u^2+n)^2-4u^2=\left ((1+c)^2-u^2\right)\left ((1-c)^2-u^2\right)$$

所以

$$\mathrm {d} s=\frac {1}{2}\left (\mathrm {d} u+\frac {1}{2}\sqrt {\frac {(1+c)^2-u^2}{(1-c)^2-u^2}}\mathrm {d} u+\frac {1}{2}\sqrt {\frac {(1-c)^2-u^2}{(1+c)^2-u^2}}\mathrm {d} u\right)$$

Landen 给出了这个式子的几何含义。右侧括号中第二项与长短半轴为$(1+c)/2,\sqrt {c}$的椭圆的弧长微分关联，第三项与实虚半轴为$(1-c)/2,\sqrt {c}$的双曲线的弧长微分直接关联。这就给出了 Landen 自己著作序言中那一段话的全部含义。而他的发现与 Gauss 的关系，只有在后续的研究中才能搞清楚。