从钢琴调音谈数学与音乐
闰馀成岁, 律吕调阳。—— $\langle$千字文$\rangle$。
音乐和数学, 两者都博大精深, 却又非常抽象。可以说, 音乐和数学是人类所创造的最了不起的文化。这个演讲里, 我们来谈一谈音乐与数学的奇妙联系。
1. 大自然的规律
大自然运行的规律告诉我们, 一个物体以频率 $v$ 震动时, 也会同时以频率 $2v, 3v, \dots$ 震动。因此若此物体震动发出了频率为 $v$ 的音高, 它也同时发出频率为 $2v, 3v, \dots$ 的音高。这些音叫做泛音。在音乐上, 从 $v$ 发出的音高到 $2v$ 发出的音高称为一个八度(听起来就是低音 Do 到高音 Do 的感觉)。从 $2v$ 发出的音高到 $3v$ 发出的音高称为一个完全五度 (听起来就是 Do 到 Sol 的感觉)。
泛音听得到吗? 可以。古典吉他的演奏中就有 `泛音' 的技巧。比如, 轻触弦的第十二格位置, 然后拨弦的同时把手指放开, 则同学会听到高八度的泛音。底下我们听听吉他的泛音 (示范)。为什么? 因为古典吉他第十二格的位置刚好是弦的一半长, 拨弦的同时把手指放开, 相当于用手指抵销频率 $v$ 的震动,凸显频率为 $2v$ 的震动, 这就是第一泛音。
人也是震动声带才能发出声音。所以, 理论上人的声音也有泛音。有没有可能唱出泛音, 或是同时唱两个音? 可以。西伯利亚的图瓦族 (Tuva) 有一种称为 "泛音唱法" (overtone singing) 的传统歌唱方式, 可以同时唱出两个音。听听这个例子 (播放音乐)。
即使发出相同的音高, 我们仍然能分辨不同乐器的音色 (timbre), 因为音色就是不同泛音叠合之后的结果——也许长笛的第四泛音比单簧管的第四泛音大, 诸如此类。有程序设计经验的同学可以试着写个简单的程序让电脑发出单一频率, 没有泛音的震动非常干涩, 毫无美感可言。
2. 毕达哥拉斯的音阶
传说中毕达哥拉斯 (Pythagoras (579-520 B.C.)) 路过一家铁匠店发现四个铁匠打铁的声音异常悦耳而开始研究声音。他用以下的两个规则试图建立起西洋音乐的音阶。
由 $v\to 2v$: 高八度。
由 $v\to \frac{3}{2} v$: 完全五度。
现行的西方音乐是 $12$ 音阶, 即一个八度共有 $12$ 个半音。我们按照毕达哥拉斯的两个规则可帮乐器调音: 以中央 $C$ 为基准。设这个音的频率是 $v$, 则高八度的 $C$ 频率是 $2v$, 高八度 $G$ 的频率是 $3v$。因此 $G$ 的频率是 $\frac{3}{2}v$。因此我们得到 $G$ 的频率了。
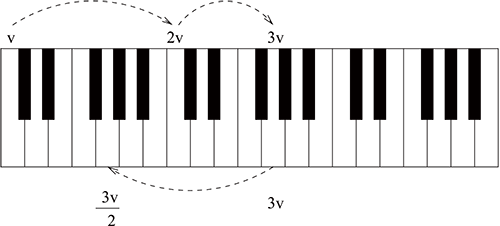
同理, 下一个得到的音是 $D$, 频率为 $\frac{9}{8}v$. 再下一个得到的音是 $A$, 频率为 $\frac{27}{16}v$。
在此我们要强调, 这个调音方法是合理的, 是符合大自然的规律的。按此我们可得到调音的顺序:$$C(=v) \to G \Big (=\frac{3}{2}v\Big ) \to D\Big(=\frac{9}{8}v\Big ) \to \cdots$$注意到每下一个音是完全五度 ($7$ 个半音), 但因为一个八度有 $12$ 个半音, 而$$\gcd(7, 12) = 1,$$因此会绕回来。这样绕一圈回来所出现的音的顺序, 称为一个五度圈。五度圈是古典音乐中所有转调与和声的基础。

我们按五度圈一直调音下去: $C\to G\to D\to A\to \cdots \to \cdots F$。此时 $F$ 的频率为 $\frac{177147}{131072}v$。按照五度圈, 再下一个要变成高音 $C$, 频率为 $\frac{177147}{131072}\times \frac{3}{2}=\frac{531441}{262144}v$。但是不要忘了原来起始的 $C$ 频率为 $v$, 因此这个高音 $C$ 的频率是 $2v$。我们得到一个非常难堪的结果:$$\frac{531441}{262144} \sim 2.02728653 \ne 2$$
同学知道这有多糟糕吧, 这告诉我们, 按照大自然的规则调音, 调出来的音阶是走音的。而且还往上走音。
3. 永远调不准
问题出在哪里? 问题在于按照五度圈调音的过程中, 每往上五度都是频率由 $v\to \frac{3}{2}v$, 每降八度都是把频率除以 $2$。上式就是 $\frac{3^{12}}{2^{18}}\ne 2$, 换句话就是$$\Big (\frac{3}{2}\Big )^{12}\ne 2^7,$$即把从 $C$ 开始每个音都走一次 (五度往上 $12$ 次) 到很高音的 $C$ (离基准的 $C$ 有 $7$ 个八度),不会等于从 $C$ 开始直接频率两倍两倍两倍 $\cdots$ 七次后走到的 $C$。
追根究底, 就是一开始打定一个八度有 12 个半音, 这是错误的抉择。那放开这个假设, 假设一个八度有若干个半音, 那按照大自然的规律, 这个若干要是多少?这相当于要求 $(\frac{3}{2})^{a}=2^b$ 的正整数解。就是要求$$2^x = 3^y$$的正整数解。很不幸, 根据算术基本定理, 这是不可能的。因此, 调音永远调不准, 不管一个八度有多少半音都一样, 反正就是想按照大自然的规律调音, 一定调不准。
这是非常令人惊吓的哲学性问题。音乐不过就是空气的震动, 所有理论的发展都应该依循着大自然的规律。但是我们用数学证明了, 整个音乐系统有根本的缺陷。
4. 调律
调律因此变成西方音乐发展中非常重要的问题。许多音乐家和理论家都试图解决这样的困境。历史发展的过程中出现了许多调律的方法。因为一定调不准, 所以不管怎么调, 就是会有一些音不对, 一些调子比较不谐和。巴哈写名为 "十二平均律" 的钢琴曲, 其中的一个意图就是为了证明所谓 "十二平均律" 的调律是可行 (人耳可以接受)的。十二平均律是一个复杂的调律方法, 在此不拟讨论。
我们已经证明了调律这个问题无解。那怎么办呢? 人们早已妥协了, 我们决定让每个音都不对。现在绝大多数的乐器调律采取等律 (equal temperament)。这是非常暴力数学的调律——把 $v\to 2v$ 的八度按等比分成 $12$ 个半音, 所以每一格为 $\sqrt[12]{2}$。(注: 十二平均律不是等律, 这是长久以来的误解。) 现代的等律调音, 多以 $A=440$ mHz 为基准, 往上往下一直乘 $\sqrt[12]{2}$ 而得到下一个音:
| 音高 | 频率 |
| 中央 $C$ | $261.625565300598634$ |
| $C^{\#}=D^{b}$ | $277.182630976872096$ |
| $D$ | $293.664767917407560$ |
| $D^{\#}=E^{b}$ | $311.126983722080910$ |
| $E$ | $329.627556912869929$ |
| $F$ | $349.228231433003884$ |
| $F^{\#}=G^{b}$ | $369.994422711634398$ |
| $G$ | $391.995435981749294$ |
| $G^{\#}=A^{b}$ | $415.304697579945138$ |
| $A$ | $440$ 标准音高 |
| $A^{\#}=B^{b}$ | $466.163761518089916$ |
| $B$ | $493.883301256124111$ |
| $C'$ | $523.251130601197269$ |
标准音高 $440$ mHz 到底听起来多高? 随便拿一支电话起来听。话筒中长长的 "嘟——" 声, 音高就是 $440$ mHz。有些音乐家喜欢把乐器音高调高一点, 听起来会比较亮。事实上, 标准音 $A$ 的频率要调多高, 在音乐史上一直变来变去。三十年前, $A=440$ mHz 是标准的, 但是现在调 $A=442$ mHz 似乎快要凌驾 $A=440$ mHz, 变成主流了。现在不少演出场地在出租钢琴时, 都会顺便询问演奏者要把基准的 $A$ 调成 $440$mHz 还是 $442$mHz。每个人的习惯不同, 那合奏时怎么办呢? 所以演出前一定要调音。下次听管弦乐音乐会时可以注意节目一开始乐团的调音——双簧管首席会吹一个 $A$,整个乐团的其他乐器就必须以这个 $A$ 为基准, 不管这个音是 $A=440$ 还是 $A=442$。
用等律调音, 两个音之间的比例是固定的。由 $C$ 到 $G$ 的完全五度 (有 $7$ 个半音) 频率比是 $(\sqrt[12]{2})^7=1.498307077$ 倍。但回忆大自然的规律, 完全五度应是 $\frac{3}{2}=1.5$ 倍。因此等律调音中, 完全五度是往下走音的。同理, $C$ 到 $D$ 的全音(两个半音) 是 $(\sqrt[12]{2})^2=1.122462048$ 倍;但按照五度圈调音, 应该是 $\frac{9}{8}=1.125$ 倍。这样的小差距, 有些敏感的耳朵是可以听得出差别的。在这些特殊的耳朵听起来, 钢琴的每个音都走音。有些音乐家的耳朵已经到了匪夷所思的地步, 这就是所谓的 "绝对音感"。
由上面的讨论知道, "绝对音感" 是存在的 (对于音的比例特别敏锐), 这和 "绝对音高" 完全不同——"绝对音高" 是一个空泛的概念, 不过就是把音背起来而已。
5. 连分数
我们回到数学。上述音阶和调律的讨论基于 $2^{19}\sim 3^{12}$, 就是说 $(x, y)=(19, 12)$ 是 $2^x=3^y$ 的一个 `差不多的解'。还有没有其他 $(x, y)$ 也是差不多的解? 有没有方法找? 有的, 用连分数。观察 $\sqrt{2}=1+(\sqrt{2}-1)=1+\frac{1}{1+\sqrt{2}}=1+\frac{1}{2+(\sqrt{2}-1)}$, 因此迭代下去得到$$\sqrt{2} = 1 + \frac{1}{2+\displaystyle\frac{1}{2+\displaystyle\frac{1}{2+\displaystyle\frac{1}{2+\cdots}}}},$$这就是 $\sqrt{2}$ 的连分数展开式。为节省篇幅, 记为$$\sqrt{2} = [1, 2, 2, 2, 2, \dots]$$仔细想想是有点不可思议的, $\sqrt{2}$ 是无理数, 但是写成连分数后居然有这么漂亮的表示。最简洁的连分数是黄金分割:$$\frac{1+\sqrt{5}}{2} = [1, 1, 1, 1, 1, \dots]$$圆周率呢? 很不幸, $\pi$ 写成连分数后还是没什么规律$$\pi = [3, 7, 15, 1, 292, 1, 1, 1, 2, \dots]$$但神奇的是 $e$, 它的连分数表示有神奇的规律:$$e = [2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, \dots]$$
连分数有什么用?想法很简单: 既然无限多层后是原来的数, 所以只取有限多层, 就是此数的近似值。比如 $\sqrt{2}=[1, 2, 2, \dots]$, 取 $[1], [1, 2], [1, 2, 2], [1, 2, 2, 2], [1, 2, 2, 2, 2], \dots$ 展开后为$$1, \frac{3}{2}, \frac{7}{5}, \frac{17}{12}, \frac{41}{29}, \dots,$$这些分数就可以当作 $\sqrt{2}$ 的近似值。
黄金比例 $\phi=\frac{1+\sqrt{5}}{2}$ 的渐近分数是什么?$$1, \frac{2}{1}, \frac{3}{2}, \frac{5}{3}, \frac{8}{5}, \frac{13}{8}, \frac{21}{13}, \frac{34}{21}, \dots$$就是相邻两项费波那契数的比例!直觉上取愈多层, 这个近似值会愈好。对。而且不只如此, 连分数还是最好的! 看底下这个神奇的结果:
Theorem 5.1. 对于无理数 $x=[a_0, a_1, \dots]$,假设 $\frac{p_n}{q_n}:=[a_0, a_1, \dots a_n]$ 为 $x$ 的第 $n$ 个渐近分数。则对于任意整数 $0\lt q \le q_n$, 都有$$\Big |x - \frac{p_n}{q_n}\Big | \lt \Big |x - \frac{p}{q}\Big |$$
即, 在所有分母小于 $q_n$ 的整数中, $\frac{p_n}{q_n}$ 是 $x$ 的最佳近似值。
来看看 $\pi$ 的近似值。取连分数, 得到渐近分数$$3, \frac{22}{7}, \frac{333}{106}, \frac{355}{113}, \frac{103993}{33102}, \dots$$非常令人吃惊的是, $\frac{22}{7}$ 和 $\frac{355}{113}$ 就是祖冲之算出来的疏率和密率。所以祖冲之不止得出 $\frac{355}{113}$ 这个分数, 这个分数还是所有分母不超过 $113$ 的分数之中, $\pi$ 的最佳近似值!祖冲之的神奇密率领先了西方整整一千年, 这真是不简单。他怎么弄出来的? 没人知道。祖冲之难道不会继续往下找下一个分数吗? 我猜他会。但数学告诉我们, 下一个更好的逼近是 $\frac{103993}{33102}$, 差太远了。以人力可以达的范围内, 祖冲之的密率已经做到顶了。因此华罗庚猜测祖冲之已经有连分数的概念, 是合理的猜测。
用渐近分数来当近似值, 够不够好? 误差有多大? 也有一个简洁的结果:
Theorem 5.2. 用 $\frac{p_n}{q_n}$ 来当作 $x$ 的近似值, 误差可由下式估计:$$\Big |x - \frac{p_n}{q_n}\Big | \lt \frac{1}{q_nq_{n+1}} \lt \frac{1}{q_n^2}$$
因此用 $\frac{355}{113}$ 当作 $\pi$, 误差已经小于 $\frac{1}{113\cdot 33102}= 0.00000026 \dots$ 了。
6. 回到调音
回到我们的音阶问题。要找 $2^x=3^y$ 的 "差不多的解", 两边取对数, 得 $\frac{x}{y}=\log _2 3$。所以相当于要找 $\log_2 3$ 的近似值。把 $\log_2 3$ 写成连分数得到$$\log_2 3 = [1, 1, 1, 2, 2, 3, 1, 5, 2, 23, 2, 2, 1, \dots],$$渐近分数为$$1, 2, \frac{3}{2}, \frac{8}{5}, \frac{19}{12}, \frac{65}{41}, \frac{84}{53}, \frac{485}{306}, \dots$$另一个神奇的事发生了。若取 $\frac{19}{12}$ 当作近似值, 就是原来的 "差不多的解"——这表示一个八度分成十二个半音。这个 "$12$ 音阶" 的解是大自然与西方音乐家们共同努力很久的结果, 现在我们用数学找到了。附带一提的是, 中国有五声音阶, 和 $\frac{8}{5}$ 的分母恰好一致。但奇怪的是, 在音乐史发展的轨迹中, 出现过 $19$ 音阶, $22$ 音阶, $24$ 音阶, $31$ 音阶, $34$ 音阶, $53$ 音阶,$72$ 音阶, $88$ 音阶, 但是没有 $41$ 音阶。数学告诉我们, $41$ 音阶才是合理的选择。
7. 闰年
只要遇到要取近似值的问题, 用连分数都管用。地球绕太阳一周称为一年, 一年其实是 $365.24219878 \cdots$ 天。因此每隔几年就会多出完整的一天。怎么闰年? 取 $0.24219878$ 连分数, 然后取渐近分数, 得到$$\frac{1}{4}, \frac{7}{29}, \frac{8}{33}, \frac{31}{128}, \frac{163}{673}, \frac{1009}{4166}, \dots$$因此每四年闰一天, 但每二十九年闰七天, 但每三十三年闰八天, $\ldots$现行的每四年闰年一次, 但是每一百年不闰, 四百又闰, 其实就是要凑到刚好。更详细的讨论可参考 [3]。
8. 结语
数学无处不在, 这篇文章算是一个小小的例子。文中的题材大部分取自 [1], 加上笔者个人的经验。不少数学家有很高的音乐造诣, 我想这不是偶然的, 因为抽象思考是人类的天赋, 而数学和音乐是最抽象的艺术。
如内文, 如果坚持连分数中每个分子都是 $1$, 那 $\pi$ 的确不好看。但是如果没有这个坚持, 连 $\pi$ 都有很漂亮的展开式, 比如$$\pi = 3 + \frac{1}{6+\displaystyle\frac{9}{6+\displaystyle\frac{25}{6+\displaystyle\frac{49}{6+\dots}}}}.$$
连分数在数学发展中有一定的地位, 但是在现代数学中没有受到很大的重视, 也许未来会有复兴的时候。
调律在音乐史理论中是非常复杂的, 历史上至少出现过有几十种不同的调律方法, 材料足以写一本专书。有兴趣的同学可参考 [2]。
回到毕达哥拉斯的四个铁匠, 传说他们用的铁锤分别重 $12:9:8:6$。因为 $12:9=8:6=$ 完全四度, $12:8 = 9:6 =$ 完全五度, $12:6=$ 八度, $9:8=$大二度,因此毕达哥拉斯听到的打铁声就是 $Do$, $Fa$, $Sol$, 高音 $Do$ 这四个音, 难怪会异常悦耳。不过真正的情形已经不可考, 就当作浪漫的故事吧——就像 "闰馀成岁, 律吕调阳",就是这么巧, 都和连分数有关!
最后谢谢彰化师范大学数学系的演讲邀约, 以及审稿学者细心的修正。
参考文献
E. Dunne and M. McConnell, Pianos and Continued Fractions,Mathematics Magazine, Vol. 72, No. 2, 104-115, 1999.
O. Jorgensen, Tuning: Containing the Perfection of Eighteenth-Century Temperament;The Lost Art of Nineteenth Century Temperament; and The Science of Equal Temperament.Michigan State University Press, 1991.
林聪源, 认识连分数, 数学传播第二卷第三期。网路版 http://episte.math.ntu.edu.tw/articles/mm/mm_02_3_08/index.html
| 作者: | 游森棚,高雄大学应用数学系 |
| 来源: | 数学传播,第 33 卷第 1 期 https://web.math.sinica.edu.tw/mathmedia/HTMLarticle18.jsp?mID=33102 |




