数学与音乐
在这一轮课程改革中,“数学与文化”成为了数学和数学教育工作者最为关注的问题之一。实际上,在很长一段时间内,许多数学和数学教育工作者已经在思考和研究这个问题,在即将推行的“高中数学课程标准”中,明确的要求把“数学文化”贯穿高中课程的始终。对于涉及“数学文化”的一系列理论问题,应该承认还没有讨论得很清楚,还有很多的争论,例如,很多学者对“数学文化”这个说法也有疑义,我们认为这是很正常的。对这些问题的研究,我们建议从两个方面同时进行,一方面进行理论上的研究; 另一方面,积极地开发一些“数学与文化”的实例,案例,课例,探索如何将“数学文化”渗透到课堂教学中,如何让学生从“数学文化”中提高数学素养,在此基础上再进行一些理论上的思考,从实践到理论,做一些实证研究。下面是我们提供的一个实例——数学与音乐,也可以看作一个素材,很希望工作在一线的教师能作进一步的开发,能使这样的素材以不同的形式进入课堂或课外活动。我们也希望有更多的人来开发这样的素材,并希望这些素材能出现在教材中。
在数学课程标准的研制过程中,我们结识了一些音乐界的专家,他们给我们讲述了很多音乐和数学的联系,数学在音乐中的应用,他们特别强调,在计算机和信息技术飞速发展的今天,音乐和数学的联系更加密切,在音乐理论、音乐作曲、音乐合成、电子音乐制作等等方面,都需要数学。他们还告诉我们,在音乐界,有一些数学素养很好的音乐家为音乐的发展做出了重要的贡献。他们和我们都希望有志于音乐事业的同学们学好数学,因为在将来的音乐事业中,数学将起着非常重要的作用。
《梁祝》优美动听的旋律,《十面埋伏》的铮铮琵琶声,贝多芬令人激动的交响曲,田野中昆虫碉啾的鸣叫……当沉浸在这些美妙的音乐中时,你是否想到了它们与数学有着密切的联系?
其实,人们对数学与音乐之间联系的研究和认识可以说源远流长。这最早可以追溯到公元前六世纪,当时毕达哥拉斯学派用比率将数学与音乐联系起来[1]。他们不仅认识到所拨琴弦产生的声音与琴弦的长度有着密切的关系,从而发现了和声与整数之间的关系,而且还发现谐声是由长度成整数比的同样绷紧的弦发出的。于是,毕达哥拉斯音阶 (the Pythagorean Scale) 和调音理论诞生了,而且在西方音乐界占据了统治地位。虽然托勒密 (C. Ptolemy,约 100-165 年) 对毕达哥拉斯音阶的缺点进行了改造,得出了较为理想的纯律音阶 (the Just Scale) 及相应的调音理论,但是毕达哥拉斯音阶和调音理论的这种统治地位直到十二平均律音阶 (the tempered Scale) 及相应的调音理论出现才被彻底动摇。在我国,最早产生的完备的律学理论是三分损益律,时间大约在春秋中期,《管子•地员篇》和《吕氏春秋•音律篇》中分别有述;明代朱载堉 (1536-1610) 在其音乐著作《律学新说》对十二平均律的计算方法作了概述,在《律吕精义・内篇》中对十二平均律理论作了论述,并把十二平均律计算的十分精确,与当今的十二平均律完全相同,这在世界上属于首次。由此可见,在古代,音乐的发展就与数学紧密地联系在了一起。从那时起到现在,随着数学和音乐的不断发展,人们对它们之间关系的理解和认识也在不断地加深。
感觉的音乐中处处闪现着理性的数学。
1. 乐谱的书写离不开数学
如今人们记录音乐最常用的方法是简谱和五线谱,它们都与数学有密切的联系。简谱不正是用阿拉伯数字 1、2、3、4、5、6、7 来表示 do、Re、Mi、Fa、Sol、La、Si 的吗? 难怪有人开玩笑说,学音乐要上达到 8。为什么呢? 因为阿拉伯数字 8 在五线谱中也发挥着重要的作用,它常常在器乐谱中以  或
或  的面目出现,这就是移动八度记号。如果
的面目出现,这就是移动八度记号。如果  标记在五线谱的上方,那么虚线内的音符要移高一个八度演奏,而
标记在五线谱的上方,那么虚线内的音符要移高一个八度演奏,而  标记在五线谱的下方,显然虚线内的音符要移低一个八度演奏。另外还要下达到 0,因为在简谱中 0 表示休止符。再看简谱和五线谱上,一般都会出现
标记在五线谱的下方,显然虚线内的音符要移低一个八度演奏。另外还要下达到 0,因为在简谱中 0 表示休止符。再看简谱和五线谱上,一般都会出现  = 60,
= 60, = 96,
= 96, = 132 这样的标记,这种标记就是用来表示音乐进行的快慢的,即音乐的速度。比如,比如
= 132 这样的标记,这种标记就是用来表示音乐进行的快慢的,即音乐的速度。比如,比如  = 132 就表示以四分音符为单位拍,每分钟 132 拍。此外,在每一首乐曲的开头部分,我们总能看到一个分数,比如,2/4、3/4、3/8、6/8 等,这些分数是用来表示不同拍子的符号,即是音乐中的拍号(the Time Signature),其中分数的分子表示每小节单位拍的数目,分母表示单位拍的音符时值,即表示以几分音符为一拍。拍号一旦确定,那么每小节内的音符就要遵循由拍号所确定的拍数,这可以通过数学中的分数加法法则来检验、比如,
= 132 就表示以四分音符为单位拍,每分钟 132 拍。此外,在每一首乐曲的开头部分,我们总能看到一个分数,比如,2/4、3/4、3/8、6/8 等,这些分数是用来表示不同拍子的符号,即是音乐中的拍号(the Time Signature),其中分数的分子表示每小节单位拍的数目,分母表示单位拍的音符时值,即表示以几分音符为一拍。拍号一旦确定,那么每小节内的音符就要遵循由拍号所确定的拍数,这可以通过数学中的分数加法法则来检验、比如,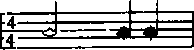 和
和 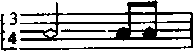 就符合由拍号 4/4 和 3/4 分别所确定的拍数,因为 1/2 + 1/4 + 1/4 = 4/4,1/2 + 1/8 + 1/8 = 3/4;而又因为 1/16 + 1/2 + (1/4 + 1/8) = 15/16 ≠ 4/4,1/8 + 1/2 二 5/8 ≠ 3/4,所以
就符合由拍号 4/4 和 3/4 分别所确定的拍数,因为 1/2 + 1/4 + 1/4 = 4/4,1/2 + 1/8 + 1/8 = 3/4;而又因为 1/16 + 1/2 + (1/4 + 1/8) = 15/16 ≠ 4/4,1/8 + 1/2 二 5/8 ≠ 3/4,所以 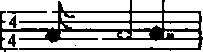 和
和 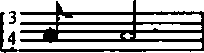 不符合由拍号 4/4 和 3/4 分别所确定的拍数。这些看似简单的要求正是音乐作曲的基础。
不符合由拍号 4/4 和 3/4 分别所确定的拍数。这些看似简单的要求正是音乐作曲的基础。
2. 钢琴键盘上的数学
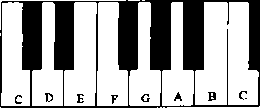 图 1
图 1
看一下乐器之王——钢琴的键盘吧,其上也恰好与斐波那契数列有关。我们知道在钢琴的键盘上,从一个 C 键到下一个 C 键就是音乐中的一个八度音程(如图 1)。其中共包括 13 个键,有 8 个白键和 5 个黑键,而 5 个黑键分成 2 组,一组有 2 个黑键,一组有 3 个黑键。2、3、5、8、13 恰好就是著名的斐波那契数列中的前几个数、
3. 音乐中的等比数列
如果说斐波那契数在钢琴键上的出现是一种巧合,那么等比数列在音乐中的出现就决非偶然了:1、2、3、4、5、6、7、i 等音阶就是利用等比数列规定的。再来看图 1,显然这个八度音程被黑键和白键分成了 12 个半音,并且我们知道下一个 C 键发出乐音的振动次数(即频率)是第一个 C 键振动次数的 2 倍,因为用 2 来分割,所以这个划分是按照等比数列而作出的。我们容易求出分割比 $x$,显然 $x$ 满足 $x^{12}=2$,解这个方程可得 $x$ 是个无理数,大约是 $1.06$。于是我们说某个半音的音高是那个音的音高的 $1.06$ 倍,而全音的音高是那个音的音高 $1.06^{2}$ 倍。实际上,在吉它中也存在着同样的等比数列[3]
4. 音乐中的数学变换
 图 2
图 2
数学中存在着平移变换,音乐中是否也存在着平移变换呢? 我们可以通过图 2 的两个音乐小节[2]来寻找答案。显然可以把第一个小节中的音符平移到第二个小节中去,就出现了音乐中的平移,这实际上就是音乐中的反复。把图 2 的两个音节移到直角坐标系中,那么就表现为图 3、显然,这正是数学中的平移。我们知道作曲者创作音乐作品的目的在于想淋漓尽致地抒发自己内心情感,可是内心情感的抒发是通过整个乐曲来表达的,并在主题处得到升华,而音乐的主题有时正是以某种形式的反复出现的。比如,图 4 就是西方乐曲 When the Saints Go Marching In 的主题[2],显然,这首乐曲的主题就可以看作是通过平移得到的。
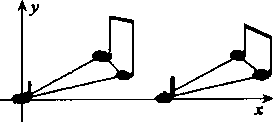 图 3
图 3
 图 4
图 4
如果我们把五线谱中的一条适当的横线作为时间轴 (横轴 $x$),与时间轴垂直的直线作为音高轴 (纵轴 $y$,那么我们就在五线谱中建立了时间-音高的平面直角坐标系。于是,图 4 中一系列的反复或者平移,就可以用函数,近似地表示出来[2],如图 5 所示,其中 $x$ 是时间,$y$ 是音高。当然我们也可以在时间-音高的平面直角坐标系中用函数把图 2 中的两个音节近似地表示出来。
在这里我们需要提及十九世纪的一位著名的数学家,他就是约瑟夫•傅里叶 (Joseph Fourier),正是他的努力使人们对乐声性质的认识达到了顶峰。他证明了所有的乐声,不管是器乐还是声乐,都可以用数学式来表达和描述,而且证明了这些数学式是简单的周期正弦函数的和[1]。
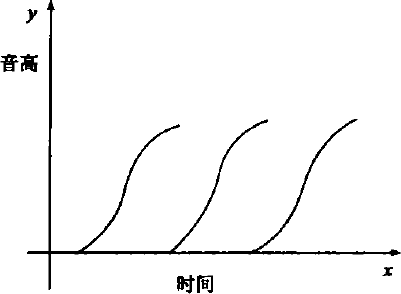 图 5
图 5
音乐中不仅仅只出现平移变换,可能会出现其他的变换及其组合,比如反射变换等等。图 6 的两个音节就是音乐中的反射变换[2]。如果我们仍从数学的角度来考虑,把这些音符放进坐标系中,那么它在数学中的表现就是我们常见的反射变换,如图 7 所示。同样我们也可以在时间-音高直角坐标系中把这两个音节用函数近似地表示出来。
 图 6
图 6
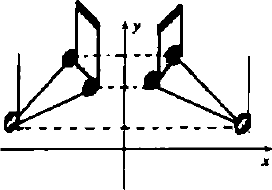 图 7
图 7
通过以上分析可知,一首乐曲就有可能是对一些基本曲段进行各种数学变换的结果。
6. 大自然音乐中的数学
大自然中的音乐与数学的联系更加神奇,通常不为大家所知。例如[2],蟋蟀鸣叫可以说是大自然之音乐,殊不知蟋蟀鸣叫的频率与气温有着很大的关系,我们可以用一个一次函数来表示:
$$C=4 t-160$$其中 $C$ 代表蟋蟀每分钟叫的次数 $t$ 代表温度。
按照这一公式,我们只要知道蟋蟀每分钟叫的次数,不用温度计就可以知道天气的温度了!
7. 理性的数学中也存在着感性的音乐
由一段三角函数图像出发,我们只要对它进行适当的分段,形成适当的小节,并在曲线上选取适当的点作为音符的位置所在,那么就可以作出一节节的乐曲。由此可见,我们不仅能像匈牙利作曲家贝拉・巴托克那样利用黄金分割来作曲,而且也可以从纯粹的函数图像出发来作曲。这正是数学家约瑟夫•傅里叶的后继工作,也是其工作的逆过程。其中最典型的代表人物就是 20 世纪 20 年代的哥伦比亚大学的数学和音乐教授约瑟夫•希林格 (Joseph Schminger),他曾经把纽约时报的一条起伏不定的商务曲线描述在坐标纸上,然后把这条曲线的各个基本段按照适当的、和谐的比例和间隔转变为乐曲,最后在乐器上进行演奏,结果发现这竟然是一首曲调优美、与巴赫的音乐作品极为相似的乐曲[2]!这位教授甚至认为,根据一套准则,所有的音乐杰作都可以转变为数学公式。他的学生乔治•格什温 (George Gershwin) 更是推陈出新,创建了一套用数学作曲的系统,据说著名歌剧《波吉与贝丝》(Porgy and Bess)就是他使用这样的一套系统创作的。
因而我们说,音乐中出现数学、数学中存在音乐并不是一种偶然,而是数学和音乐融和贯通于一体的一种体现。我们知道音乐通过演奏出一串串音符而把人的喜怒哀乐或对大自然、人生的态度等表现岀来,即音乐抒发人们的情感,是对人们自己内心世界的反映和对客观世界的感触,因而它是用来描述客观世界的,只不过是以一种感性的或者说是更具有个人主体色彩的方式来进行。而数学是以一种理性的、抽象的方式来描述世界,使人类对世界有一个客观的、科学的理解和认识,并通过一些简洁、优美、和谐的公式来表现大自然。因此可以说数学和音乐都是用来描述世界的,只是描述方式有所不同,但最终目的都是为人类更好地生存和发展服务,于是它们之间存在着内在的联系应该是一件自然而然的事。
既然数学与音乐有如此美妙的联系,为何不让我们沉浸在《梁祝》优美动听的旋律中或置身于昆虫碉啾鸣叫的田野里静下心来思考数学与音乐的内在联系呢? 为何不让我们在铮铮琵琶声中或令人激动的交响曲中充满信心地对它们的内在联系继续探索呢?
上面,我们提供了一些数学与音乐联系的素材,如何将这些素材“加工”成为“数学教育”的内容呢?我们提出几个问题仅供教材编写者和在一线工作的教师思考。
1. 如何将这样的素材经过加工渗透到数学教学和数学教材中?
2. 能否把这些素材编写成为“科普报告”,在课外活动中,向音乐和数学爱好者报告。调查了解,思考这样的报告对学生的影响以及学生对这样的报告的反映。
參考文献:
M. Kline. 西方文化中的数学。张祖贵译,九章出版社。台湾,1984
T. H. Garland and C. V. Kahn, Math and Music:Harmonious Comuxtions, Dale Deymour Publications. 1995
川久保胜夫•数学的奧秘•李景华译•北京:科学出版社。2003
西奧妮•帕帕斯•数学的奇妙•陈以鸿译•上海:科技教育出版社,1999
贾方爵•基本乐理。重庆:西南师范大学出版社。2003
| 作者简介: | 刘卫锋,首都师范大学数学系教授 |
| 王尚志,首都师范大学数学系教授 | |
| 来源: | 数学通报 2005 年第 44 卷第 4 期 |




