2015 年，笔者在准备一篇关于数论中的平方和问题的历史综述时，第一次了解到刘治国教授的杰出工作。后来我从网上特地查了查他的资料，才知道他是一位历经磨难、自学成才的数学家。得知他任教于华东师范大学数学系，笔者特别委托上海交通大学的好友崔继峰博士拜访了刘治国教授，并做了记录。2017 年 2 月，我的同事张瑞明教授邀请刘治国教授来我校访问，笔者才有机会近距离接触刘教授，对他有了更直观和深切的认识。

笔者认为，刘治国教授的经历对于今天在读的学生，绝对是一个励志的传奇。接下来，就让笔者简单介绍一下刘治国教授，并将崔继峰博士和我对他的访谈（经刘治国教授本人过目）分享给各位读者。

刘治国，华东师范大学数学系教授，博士生导师。1963 年生于河南焦作武陟县，1979 年 16 岁考入河南师范大学数学系，1983 年毕业。先后任教于中学和新乡教育学院。在工作之外，刘治国刻苦钻研数学，因偶然的机会，接触到印度天才数学家拉马努金（Ramanujan）的工作，刘治国从中得到灵感，在 $\theta$–函数、$q$–级数、数论等领域得到了丰硕成果，震惊了国际上研究拉马努金工作的专家。1998 年，在英国数学家刘易斯（Lewis）博士的努力下，英国皇家学会破格授予只有学士学位的刘治国 “王宽诚皇家学会研究奖学金”，他出国访学一年。2001-2003 年，新加坡国立大学数学系曾衡发教授邀请刘治国访问合作。2003 年，刘治国被华东师范大学数学系直接聘为教授。

刘治国教授的工作与拉马努金的工作密切相关。众所周知，拉马努金的工作以富于创作性同时也难以理解而著称，数学大师哈代（Hardy）和塞尔（Serre）等都曾对拉马努金的工作加以解读诠释，而破译拉马努金工作的数学家就更是举不甚举了。不同于许多数学家攻坚拉马努金遗留的个别猜想，刘治国教授试图建立一套一般的理论来解释 Ramanujan 众多奇妙公式的来源，并揭示出相关数学领域的全貌。

谈到拉马努金，刘教授充满了崇拜之情，他常常用 “有灵性” 来评价拉马努金的工作。谈到他本人的工作，刘治国教授则充满了自信。刘教授说：“研究数学要有长远的打算，不要急功近利， 要有敢为天下先的想法，创立属于自己的数学领域。”

刘教授认为，他之所以能取得现在的成绩，除了他的勤奋刻苦之外，很重要的一点是，他是一个单纯的数学人。他说，做数学的乐趣是无穷的。他本人没有硕士、博士学历（1983 年曾报考山东大学潘承洞教授的硕士生，1984 年报考云南大学的硕士研究生，1985 年报考过北京大学丁石孙教授的硕士研究生，可惜的是，命运不济，居然三次落榜），这确实给他造成了一些身外的损失，但刘教授并不计较，因为他有信心，他的定理可以流传千古。这让我们想起杜甫的名句： “文章千古事”。

刘教授说，他在读本科时翻开数学书，发现书上没有一个定理是以中国人的名字命名的，非常失望。从那时起，他便立志，要创造出自己的定理。刘教授未忘初心，一直做着好的数学，创造美妙的定理。

回顾他本人的求学之路，刘教授用 “西天取经” 来形容。这个比喻确实贴切。一方面，被誉为 “神人” 一般的印度数学家拉马努金的工作，指引着他寻找真理（经）；另一方面，刘治国教授确实历经坎坷。当年连本科学位都没有拿到的拉马努金，被哈代慧眼识中，邀请到剑桥深造合作。在哈代的提携庇护下，拉马努金简直就是一路绿灯畅通无阻，甚至当选为英国皇家学会会员，此后被印度人一直视为学术偶像乃至民族的骄傲，近来甚至到了奉若神明的地步。

论数学成就，刘治国教授固然不宜与前辈拉马努金比较，但他的故事同样激励今天的年轻人，同样值得我们去了解。

刘治国教授访谈

崔继峰访问 林开亮整理

采访时间：2015.09.09，13:00-16:10

参访地点：华东师范大学闵行校区数学系 336 室

因数学而改变命运

崔：请问您是否在小学和中学就对数学有兴趣? 是不是从小就听说过华罗庚、陈景润等数论学家的故事?

刘：我中小学喜欢学习数学，但并没有表现出特别浓厚的兴趣。小时候从大人们那里听说过一些关于华罗庚的一些故事，只知道他是位了不起的大数学家，是我们国家和民族的骄傲，但并未真正懂得他在研究什么。我是 1977 年上的高中，上高中后又知道了陈景润的故事，感到特别激动和自豪，觉得我们中国数学家太了不起了。

崔：您在哪里读的本科，为什么选择数学专业？当时是否有什么课程特别吸引您，为什么? 有没有哪个老师或哪本书对您有特别大的影响? 您是否做出一些成果？

刘：我本科就读于新乡师范学院（1985 年始改称河南师范大学），1979 年高考过后我的成绩只能上普通大学，我想申请进入农业和水利方面的院校学习农学或水利学，但我的班主任慕博文老师和数学老师任中卫觉得我有一些数学才能，劝我报考了新乡师范学院的数学专业。

大学的《复变函数》课程吸引了我，因为我发现留数理论可以被用来计算实积分，其基本方法是：首先将要计算的关于实函数的定积分化为复变函数沿闭回路曲线的积分，再用留数基本定理化为被积函数在闭合回路曲线内部孤立奇点上求留数的计算，当奇点是极点的时候，计算更加简洁。

大学期间，我在《中学数学研究》上发表（大二投稿，大三发表）了一篇数学教育方面的论文《一类特殊无理方程的简单解法》，这篇论文强调了求解方程时的参数化思想。现在看来这也许没有什么了不起，但在当时的环境下是非常不容易的。 我还研究了一些高次丢番图方程的公式求解问题，但没有整理发表，我记得我大学毕业论文就讨论了一个高次丢番图方程的求解问题。

崔：您 1983 年本科毕业，1985 年才到一所地方成人高校工作，中间两年您做什么了？您本科毕业后一直处在一个孤立的环境下做研究，是否有成果，是否引起国内同行的关注？如何想到要跟外界联系？国内哪些教授对您影响比较大？

刘：中间两年分别在家乡的两所乡办高中教书（武陟县北郭高中和圪垱店高中，现在已撤销）。本科毕业后的这些年里，我做过一些比较初等的分析不等式、级数求和以及偏微分方程求解的研究，在国内的一些大学学报上发表了 10 多篇论文。以我现在的眼光来看，有些结果还是很有意思的，但由于都发表在国内的一些普通刊物上，所以并没有引起多少学术反响。

在大量地阅读了国外期刊的论文后，我萌发了与国外取得联系的念头。当然开始和国外的数学家联系时我并没有向他们推销我的研究结果，我写信给他们只是希望能得到他们论文的抽印本，因为对我来讲获取资料很困难。

我研究数学早期对我影响最大的书有三本，分别是：王竹溪和郭敦仁的《特殊函数概论》（科学出版社，1965 年），徐利治和王兴华的《数学分析的方法及例题选讲》（高等教育出版社，1984 年）, 以及 George Pólya 和 Gábor Szegő 编著的《数学分析中的问题和定理》(张奠宙和宋国栋等译, 上海科学技术出版社，1981 年)。

崔：您人生中的转折点是否因此而出现，在哪一个时刻？

刘：我个人觉得转折点有：

1. 考上高中和大学。

2. 离开中学到新乡教育学院（现在已经并入新乡学院）工作，这所学校本身没有什么科研条件，但相对高中来讲课没有那么多，我可以抽出更多的时间考虑数学问题，而且也方便我去河南师大数学系资料室查阅资料。我非常感激当时河南师大数学资料室的两位资料管理员，她们像对待河南师大数学系的教师一样对待我，我在这里查资料的时间断断续续持续了五六年时间。

3. 看到伊利诺斯大学数学系 Bruce C. Berndt 教授在《美国数学月刊》发表的关于 Ramanujan 季度报告里中的 Ramanujan 主定理（Ramanujan's master theorem）。

4. 在 Lewis 博士的努力下，我于 1998 年获得英国皇家学会研究奖学金并在英国访问一年，这标志着我开始逐渐融入研究 Ramanujan 遗留数学问题的学术圈。

（Lewis 博士已经于 2007 年因病去世，享年 65 周岁，我到华东师大工作以后曾计划邀请他来华访问，可惜他因为身体问题未能成行）。

5. 当代杰出的数论专家，国际数学界研究圆周率的权威新加坡国立大学的曾衡发（Chan Heng Huat）教授给予了我极大的支持，曾于 2001 年 6 月至 2003 年 4 月邀请我到新加坡国立大学和他进行合作研究。

6. 新加坡访问期间巧遇我国著名的代数几何专家，华东师范大学谈胜利教授，谈教授慧眼识珠，将我引荐到华东师范大学。

崔继峰（图右）在采访刘治国教授。

妙不可言的灵光一现

崔：您在思索问题时，是否曾有一个灵光一闪的瞬间，一个爆发性的时刻，就像阿基米德发现了浮力定律竟兴奋得从澡盆里冲出来忘情裸奔？

刘：应该有过几次。当 1993 年我猜到关于 $q$–级数的一个一般展开公式并发现该公式包含了几乎所有已知的著名 $q$–级数公式为特例时，我激动的心情就像在田野里漫游的人突然发现了一个宝藏而兴奋不已。学过 $q$–级数的人都知道，$q$–级数中很多神奇的公式基本上都来自伟大的数学家之手，如欧拉（Euler）、高斯（Gauss）、雅可比（Jacobi）、西尔维斯特（Sylvester）、罗格斯（Rogers）、拉马努金（Ramanujan）、华森（Watson）、杰克森（Jackson）、海涅（Heine）、贝利（Bailey）、卡利茨（Carlitz）、塞尔伯格（Selberg）、安德鲁斯（Andrews）、阿斯基（Askey）等。 我竟然碰巧找到一个更一般的统一公式，统一和概括了他们的结果，我实在是兴奋不已，这极大增强了我继续研究数学的信心。在相当长一段时间内，我都不敢相信这是事实，因为我觉得，只有大数学家才有能力去发现这样的公式，而我实在是太普通了。直到 1998 年我在英国遇到同在 Sussex 大学访问的安德鲁斯教授，当面向他解释了我的这一发现，得到了他的肯定，我才相信我真的有了一个很好的数学发现。我觉得我太幸运了，感受到这是上苍赐给我的礼物。这个公式在 2002 年的 Ramanujan Journal 发表。

2012 年在印度参加学术会议和 Askey 教授（左一）、Andrews 教授（左二）、Berndt 教授（右二）合影，右一为刘治国。（供图：刘治国）

崔：报道中提到，您从 1983 年某一期《美国数学月刊》偶然看到伊利诺斯大学数学系 Bruce C. Berndt 教授写的关于 Ramanujan 季度报告的一篇论文，这个机缘让您首次了解到 Ramanujan 的工作，并从 Ramanujan 的一个公式中悟出了灵感。具体是哪个结果让您感觉有灵光闪过？

刘：该文主要是介绍 Ramanujan 在数学分析领域里的一项贡献，当我看到这篇文章的头一个定理即所谓的 Ramanujan 主定理^[1]（编注：定理见下图）时，我确实感觉瞬间心领神会。

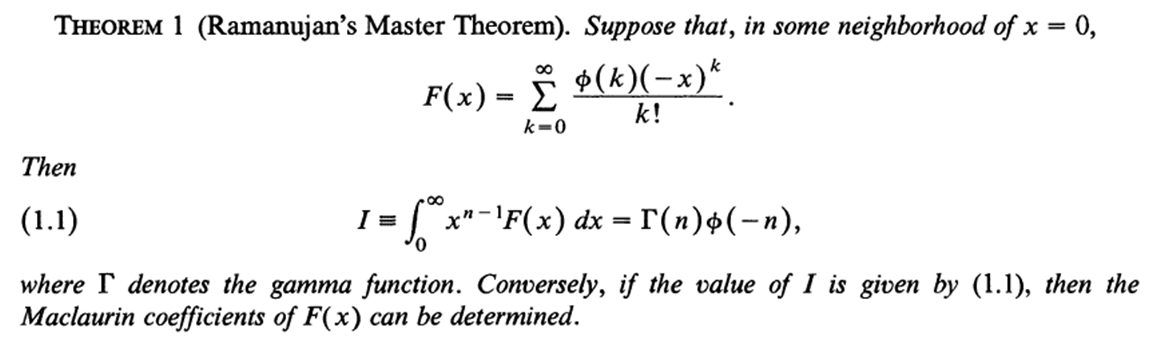
崔：您从这个公式是不是立即看出它含有更多的东西？或者说，您看到这个公式，是不是已经感觉到这只是浮现出来的冰山一角，下面藏着一个无穷无尽的世界？

刘：当看到 Berndt 的论文中 Ramanujan 主定理时，我激动的心情难以用言语表达。这个集简洁性和广泛性于一体的积分定理，提供了一种计算定积分的有效便捷方法。该定理使我对数学有了全新的认识，激发了我的数学潜力， 找到了自己感兴趣的数学课题。我的确感到这只是浮现出来的冰山一角，感到即便是像数学分析这样经典的课题，我们所了解的还远远不够。

拉马努金式求学

崔：就像当年 Ramanujan 写信给英国的大数学家一样，您也写信给英美的数学家。并且，就像 Ramanujan 得到了哈代（Hardy）的赏识一样，您也得到了国外同行的认可和赏识。像他的前辈哈代一样，Lewis 教授也推荐您到英国进修访问。您并没有研究生学历，当时申请皇家学会的奖学金是不是一帆风顺？

刘：我刚开始并没有向国外数学家推销自己的想法，我写信向 Lewis 博士索要他论文的抽印本，他愉快地给我寄来了他论文的抽印本并附了一封信，他在信中问我有没有关于 $q$–级数的研究结果。这样我们就开始了通信，他很快就有了让我去英国访问的想法。他向英国皇家学会提交了为我申请奖学金的申请。提交申请后，他写信给曾经担任过英国皇家学会会长的阿蒂亚（Atiyah）教授，特别说明了我的情况。阿蒂亚跟 Lewis 博士说，对来自中国和其它类似地方的申请者来说，博士学位其实没那么重要（Lewis 博士在 1997 年 3 月 24 日给我的信中这样写到：Somebody here told me that, as you do not have a PhD, you would have a little chance of getting a RS fellowship. However I wrote to Professor Atiyah, who is the most important person in British Mathematics and has been a president of the Royal Society, and he told me that a PhD is not so important for people from China and similar places. However he does say that RS fellowship are definitely only for one year. He is going to look into the matter and see what can be done）。阿蒂亚在英国数学界是泰山北斗执牛耳的人物，再加上我的工作与 Ramanujan 密切相关，我很幸运地申请到 1998 年的皇家学会奖学金。

崔：报导中说，您给 Lewis 教授和美国的 Berndt 教授写第一封自荐信时，给出了 8 个公式，正是这些公式打动了他们，就像当年 Ramanujan 凭借信中的 15 个公式打动了哈代。我很好奇，可否看看这些公式？

刘：我没有留下给 Lewis 信件的副本，时间过得太久了，记的不一定完全准确，应该是下列几个恒等式：

For $|q|<1$  and $z\not=q^m,~m=\pm 1, \pm 2, \ldots,$ we have the identity $$ \begin{aligned} &\prod_{n=1}^\infty  \frac{(1-q^n)^4}{(1-q^n z)^2 (1-q^n/z)^2}\\ &=1+(1-z)^2 \sum_{n=1}^\infty \frac{n(q/z)^n}{1-zq^n} +(1-1/z)^2 \sum_{n=1}^\infty \frac{n(qz)^n}{1-q^n/z}. \end{aligned}\tag{identities-1} $$ For $|q|<1,$ we have the following two Eisenstein series identities: $$ a(q)a(q^5)+2c(q)c(q^5)=1+6\sum_{n=1}^\infty \frac{nq^n}{1-q^n}-30\sum_{n=1}^\infty \frac{nq^{5n}}{1-q^{5n}},\tag{identities-2} $$ $$ \begin{aligned} &a(q)a(q^2)\\ &=1+6\sum_{n=1}^\infty \left(\frac{nq^n}{1-q^n}-\frac{2nq^{2n}}{1-q^{2n}} +\frac{3nq^{3n}}{1-q^{3n}}-\sum_{n=1}^\infty \frac{6nq^{6n}}{1-q^{6n}}\right), \end{aligned}\tag{identities-3} $$ where $$ \begin{aligned} a(q)&=\sum_{m, n=-\infty}^\infty q^{m^2+mn+n^2},\\ c(q)&=\sum_{m, n=-\infty}^\infty q^{(m+1/3)^2+(m+1/3)(n+1/3)+(n+1/3)^2}. \end{aligned} $$ For $|q|<1,$ we have the following two identities: $$ \begin{aligned} &\frac{\sin \frac{2\pi}{7}}{\sin \frac{\pi}{7}} \prod_{n=1}^\infty \left(\frac{1-2q^n \cos \frac{4\pi}{7}+q^{2n}}{1-2q^n \cos \frac{2\pi}{7}+q^{2n}}\right)- \frac{\sin \frac{3\pi}{7}}{\sin \frac{2\pi}{7}} \prod_{n=1}^\infty \left(\frac{1-2q^n \cos \frac{6\pi}{7}+q^{2n}}{1-2q^n \cos \frac{4\pi}{7}+q^{2n}}\right)\\ &\quad+\frac{\sin \frac{\pi}{7}}{\sin \frac{2\pi}{7}} \prod_{n=1}^\infty \left(\frac{1-2q^n \cos \frac{2\pi}{7}+q^{2n}}{1-2q^n \cos \frac{6\pi}{7}+q^{2n}}\right) =1+7q^2\prod_{n=1}^\infty \left(\frac{1-q^{49n}}{1-q^n}\right), \end{aligned}\tag{identities-4} $$ $$ \begin{aligned} &\frac{\sin ^{7} \frac{\pi}{7}}{\sin ^{7} \frac{2 \pi}{7}} \prod_{n=1}^{\infty}\left(\frac{1-2 q^{n} \cos \frac{2 \pi}{7}+q^{2 n}}{1-2 q^{n} \cos \frac{4 \pi}{7}+q^{2 n}}\right)^{7}-\frac{\sin ^{7} \frac{2 \pi}{7}}{\sin ^{7} \frac{3 \pi}{7}} \prod_{n=1}^{\infty}\left(\frac{1-2 q^{n} \cos \frac{4 \pi}{7}+q^{2 n}}{1-2 q^{n} \cos \frac{6 \pi}{7}+q^{2 n}}\right)^{7} \\ &\quad+\frac{\sin ^{7} \frac{3 \pi}{7}}{\sin ^{7} \frac{\pi}{7}} \prod_{n=1}^{\infty}\left(\frac{1-2 q^{n} \cos \frac{6 \pi}{7}+q^{2 n}}{1-2 q^{n} \cos \frac{2 \pi}{7}+q^{2 n}}\right)^{7} \\ &=289+18 \times 7^{3} q \prod_{n=1}^{\infty}\left(\frac{1-q^{7 n}}{1-q^{n}}\right)^{4}+19 \times 7^{4} q^{2} \prod_{n=1}^{\infty}\left(\frac{1-q^{7 n}}{1-q^{n}}\right)^{8}+7^{6} q^{3} \prod_{n=1}^{\infty}\left(\frac{1-q^{7 n}}{1-q^{n}}\right)^{12} \end{aligned}\tag{identities-5} $$ For $|q|<1,$ Jacobi's theta functions $\theta_1, \theta_2, \theta_3$ and $\theta_4$ are defined by $$ \begin{aligned} \theta_1(z, q)&=2q^{1/8} (\sin z)\prod_{n=1}^\infty (1-q^n) (1-2q^n \cos 2z+q^{2n}),\\ \theta_2(z, q)&=2q^{1/8} (\cos z)\prod_{n=1}^\infty (1-q^n) (1+2q^n \cos 2z+q^{2n}),\\ \theta_3(z, q)&=\prod_{n=1}^\infty (1-q^n) (1+2q^{n-1/2} \cos 2z+q^{2n-1}),\\ \theta_4(z, q)&=\prod_{n=1}^\infty (1-q^n) (1-2q^{n-1/2} \cos 2z+q^{2n-1}). \end{aligned} $$ If we use $\theta_1'(z, q)$ to denote the partial derivative of $\theta_1(z, q)$ with respect to $z,$ then, we have the following two theta function identities: $$ \begin{aligned} &1+12\sum_{n=1}^\infty \left( \frac{nq^n}{1-q^n}-\frac{3nq^{3n}}{1-q^{3n}}\right) \\ &=\frac{\theta_1'(0, q^3)^5}{\theta_1'(0, q)^3} \left(\frac{\theta_2^3(0, q)}{\theta_2^5(0, q^3)}-\frac{\theta_3^3(0, q)}{\theta_3^5(0, q^3)}+\frac{\theta_4^3(0, q)}{\theta_4^5(0, q^3)}\right), \end{aligned}\tag{identities-6} $$ $$ \begin{aligned} &1+4\sum_{n=1}^\infty \left( \frac{nq^n}{1-q^n}-\frac{7nq^{7n}}{1-q^{7n}}\right) \\ &=\frac{\theta_1'(0, q)^3}{49\theta_1'(0, q^7)} \left(\frac{\theta_2(0, q^7)}{\theta_2^3(0, q)}-\frac{\theta_3(0, q^7)}{\theta_3^3(0, q)}+\frac{\theta_4(0, q^7)}{\theta_4^3(0, q)}\right). \end{aligned}\tag{identities-7} $$ Let $\left(\frac{k}{11}\right)$ be the Legendre symbol modulo $11.$ Then we have $$ \begin{aligned} &1+2\sum_{n=1}^\infty \left(\frac{k}{11}\right) \frac{q^n}{1-q^n}\\ &=-\frac{1}{11}\sqrt{\frac{\theta_1'(0, q)^3}{\theta_1'(0, q^{11})}} \left(\sqrt{\frac{\theta_2(0, q^{11})}{\theta_2^3(0, q)}}+\sqrt{\frac{\theta_3(0, q^{11})}{\theta_3^3(0, q)}}-\sqrt{\frac{\theta_4(0, q^{11})}{\theta_4^3(0, q)}}\right). \end{aligned}\tag{identities-8} $$

崔：这些公式对您来说，是不是有生命有灵性的？

刘：这些都是关于模形式理论（modular forms）的恒等式。模形式理论是数学的一个重要分支，与数论、函数论、群论以及代数几何等众多的数学分支有关。该理论的一个特点是，有许多美妙深刻的恒等式存在，有的时候从一个恒等式出发，就可以推出数学中一个重要的定理。雅可比应该是最早研究模形式理论的数学家，他从一个关于模形式的恒等式（见下文）推出了著名的拉格朗日（Lagrange）四平方数和定理。Ramanujan 在给哈代的信件中就包含了不少关于模形式的恒等式（见附录）。尽管模形式理论已经有了将近 200 年的发展历史，但直到今天，要找出一个关于模形式的漂亮恒等式，仍然不是一件容易的事情。

追索拉马努金的奥秘

崔：我估计，Lewis 教授促成您去英国访学，更是抱着一种好奇的心理，想了解你是怎么发现和证明这些公式的，就像当年哈代邀请 Ramanujan 访问剑桥一样。传闻说，Ramanujan 说他的公式都是梦中受到神灵昭示得到的。普通人觉得他的工作极微妙、难以理解，也就把他视为神人一般的存在。您觉得呢？他的工作真的那么神秘莫测、以至于他过世了将近 100 年，我们还摸不着头脑吗？

刘：与其他许多伟大的数学家不太一样，Ramanujan 本人并没有创立系统的数学理论。但我觉得 Ramanujan 不仅是一位伟大的数学家，更是通过他的公式引导数学发展的数学大师。他的美妙富有启发意义的公式，就像灯塔一样指明了数学发展的方向。例如他关于模形式理论中著名的 $τ$ 函数积性的猜想引导德国数学家 Hecke 创立了著名的 Hecke 理论，Serre 为了解释 Ramanujan 关于 $τ$ 函数的一个同余式而发展了 $p$ 进模形式理论。100 年来，数学界关于 Rogers-Ramanujan 恒等式的研究，更是推进了 $q$–级数和组合分析的发展。关于他的仿 $θ$–函数猜想的研究更是当今数学研究的热点之一。我觉得 Ramanujan 对数学如此酷爱，已经超脱了名利的羁绊，他已经把自己和数学融为一体，达到了天人合一的境界。他对公式的感觉已经达到了出神入化的地步。如果你仔细挖掘，会发现他很多公式的后边都蕴含着深刻的数学理论。我们如果以世俗的眼光和急功近利的想法去破解所谓的 Ramanujan 之谜，我想不会有什么答案。

改编自关于拉马努金的同名小说 The Man Who Knew Infinity《知无涯者》的电影海报 (2015)

下图是 1916 年诞生的拉马努金猜想, 其中 (i)(ii) 在 1917 年被莫德尔 (Mordell) 证明, 而 (iii) 在 1974 年被德利涅 (Pierre Deligne) 证明, 后者是我们这个时代的数学领袖之一。而拉马努金猜想的一个推广, 所谓的 Maass 形式的 Ramanujan–Petersson 猜想(诞生于 1930 年), 至今仍未证明。

设数列 $\tau (n)$ 定义如下： $$q \prod _ {n = 1} ^ { \infty } \left( 1 - q ^ { n } \right) ^ { 24 } = \sum _ { n = 1 } ^ { \infty } \tau ( n ) q ^ { n }$$ 则有
(i) $\tau$ 是可乘的，即，当 $m , n$ 互素时总有 $$\tau (m n) = \tau ( m ) \tau ( n )$$ (ii) 降幂法则： 若 $p$ 是素数，则对任意的正整数 $r$ 有 $$\tau \left(p ^ { r + 1} \right) = \tau ( p ) \tau \left( p ^ { r } \right) - p ^ { 11 } \tau \left( p ^ { r - 1 } \right)$$ (iii) 对一切素数 $p$ 有，$| \tau ( p ) | \leq 2 p ^ { 11 / 2 }$

崔：您是怎么悟出成百上千个公式的？是不是发现了隐藏着的一般模式？就是说，事实上发现了生成公式的内在机制？

刘：我只是一位酷爱数学的普通人，既没有 Ramanujan 那样的天赋，也没有像他一样超凡脱俗。与 Ramanujan 相比，我微不足道。但包括 Ramanujan 在内的许多数学大师以及当代许多研究 Ramanujan 遗留问题的数学家（特别是安德鲁斯教授和阿斯基教授）的工作启迪了我的思维。在他们的基础上，我发展了研究 $θ$–函数和 $q$–级数的全新方法，正是这些新方法引导我发现了新的公式。

崔：您可否谈一谈您的两项代表性工作？估计很多朋友都想了解，您做的工作，究竟是怎样地与众不同。

刘：一个是论文《$q$–级数的一个展开公式及其应用》^[2]。在这篇论文中，我找了将任意形式幂级数展开成 $q$–级数的一个公式。因为在原点解析的复函数一定能展开成幂级数，所以这个公式其实就是找到了将在原点解析的任意复函数转换成 $q$–级数的方法。这个公式是一个融数论和分析为一体的公式，该公式蕴含了数论、组合论和分析中个数以百计著名的定理，例如欧拉五边形数定理、雅可比四平方数和定理、高斯三角数和定理、Rogers-Ramanujan 恒等式，Askey-Wilson 多项式及 $q$–雅可比多项式的正交性等等。 我认为这种融数论和分析在一起的有着广泛意义的公式在数学中并不常见，我坚信该公式仍然有极其广泛的应用前景。

刘治国（摄于 2015 年三峡。供图：刘治国）

脑补内容：

1 一个函数 $f(x)$ 的 $q$–导数（q-derivative），是其普通导数 $Df(x)$ 的 $q$–模拟，定义为^[3]$$D _ {q} f ( x ) = \frac { f ( q x ) - f ( x ) } { q x - x }$$

字母 $q$ 有多重含义：
(i) 因为通常的形式幂级数用作 $q$ 自变量（$q$–级数），这追溯到几何级数（等比数列的无穷和）$1 + q + q ^ { 2 } + \ldots$ 中的 $q$ 表示商或比（quotient）；自 Jacobi 以后，$q$ 在椭圆函数论中已经是标准的记号了；
(ii) $q$ 是量子英文单词 quantum 的首字母，关于 $q$–导数的学问也被称为量子微积分（Quantum Calculus）；
(iii) $q$ 也常用来表示一个有限域的元素个数，由此提示它与组合论、数论的关系。

2 欧拉五边形数定理：

$$\prod _ {n = 1} ^ { \infty } \left( 1 - q ^ { n } \right) = \sum _ { n = - \infty } ^ { \infty } ( - 1 ) ^ { n } q ^ { n ( 3 n + 1 ) / 2 } \quad ( | q | < 1 )$$

雅可比四平方数和定理：

$$\theta ^ {4} ( q ) = \left( \sum _ { n = - \infty } ^ { \infty } q ^ { n ^ { 2 } } \right) ^ { 4 } = 1 + 8 \sum _ { 4 \nmid d } \frac { d q ^ { d } } { 1 - q ^ { d } } \quad ( | q | < 1 )$$

高斯三角数和定理（Andrews 的表述）：

$$\left(\sum _ { n = 0} ^ { \infty } q ^ { \left( \begin{array} { c } { n + 1 } \\ { 2 } \end{array} \right) } \right) ^ { 3 } = \sum _ { n = 0 } ^ { \infty } \sum _ { j = 0 } ^ { 2 n } \frac { 1 + q ^ { 2 n + 1 } } { 1 - q ^ { 2 n + 1 } } q ^ { 2 n ^ { 2 } + 2 n - ( j + 1 ) }$$

我的第二项工作跟 $q$–偏微分方程有关。在上世纪 90 年代我接触 $q$–级数不久后，就一直在思考这样一个问题：在众多深刻的关于 $q$–级数公式的后面有没有一个起关键作用，结构简单美妙的方程呢？我坚信大道至简的哲理。那时这个想法也许太超前，因为那时关于 $q$–级数的研究文献里没有任何线索。我在相当长时间内一直没有取得任何进展。2010 年的某一天我突然醒悟，悟到这个东西应该就是一个特殊的 $q$–偏微分方程呀。就这样，$q$–偏微分方程这个概念就在我的脑海中闪现出来了。虽然从德国数学家海涅（E. Heine）1846 年的系统工作开始，人们系统研究 $q$–级数至今已经有将近 170 年的历史了，$q$–导数的概念已经有近 140 年的历史了，这期间人们还研究了 $q$–微分方程，$q$–差分方程及 $q$–积分方程，但数学界并没有人去研究 $q$–偏微分方程。也许人们觉得 $q$–微分方程的研究已经遇到了巨大的困难，没有必要去碰 $q$–偏微分方程。我决定从我认为最简单的含有两个复变数的 $q$–偏微分方程入手，这个 $q$–偏微分方程说，未知的二元复变量函数满足，关于一个变量的 $q$–偏导数等于关于另一个变量的 $q$–偏导数：$$\partial _ {q , x} f ( x , y ) = \partial _ { q , y } f ( x , y )$$

我发现，如果该方程的解在原点解析，则它可以表示为齐次 Rogers–Szegő 多项式的线性组合。我还证明了如果一个在原点解析的多元函数解析函数满足一组类似上述的 $q$–偏微分方程，则该解析函数可以展开成齐次 Rogers–Szegő 多项式乘积的线性组合。这是一个令我异常激动的数学发现。利用这个展开定理，我发展了一套系统推导 $q$–级数恒等式的方法。历史上关于 $q$–级数的许多伟大的发现，都可以由这个展开公式推出，借助这个展开定理，我们还可以发现更多新的恒等式。$q$–偏微分方程是个崭新的数学课题，更多的 $q$–偏微分方程等待着人去研究。

$q$–偏微分方程理论有机地将多复变函数理论、特殊函数论与数论结合起来，提供了研究 $q$–级数（$q$–数学）的全新的方法。 2012 年，我在印度德里大学举行的拉马努金 125 周年诞辰纪念大会上报告了我的研究成果，后来以此报告为基础写成论文《论 $q$–偏微分方程与 $q$–级数》^[4]。

脑补内容：为了帮助读者理解刘治国教授这一杰出的原创性工作，我们补充该定理的普通版本如下，引自刘治国教授的上述论文：

命题 1.5 设 $f(x,y)$ 是 $( 0,0 ) \in \mathbb { C } ^ { 2 }$ 附近的解析函数，且满足偏微分方程，$\partial _ { x } f ( x , y ) = \partial _ { y } f ( x , y )$ 则 $f ( x , y ) = f ( x + y , 0 )$。

崔：您既懂数论又懂特殊函数，是怎样的机缘巧合形成您如此独特的风格的？

刘：这两门学科有互通的地方。数学的量子化（$q$–模拟）是一个重要的思想和方法，椭圆函数和 $θ$ 函数可以看成一种特殊类型的 $q$–级数，将一些特殊函数、甚至更一般的解析函数量子化后，在很多情况下，我们自然会看到数论、组合论与分析的有机联系。

崔：您第一次写英文论文是否顺利？（因为没有人指导的话，一般人会比较害怕。）

刘：并不顺利，第一篇英文论文《$q$-Hermite Polynomials and a $q$-Beta Integral》于 1997 年发表在了《Northeast Math. J.》上，之后的英文论文写作得到了 Lewis 的大量帮助。

崔：您是否有教学任务，教什么课程？您现在带了多少个博士生？除了教学研究，您有什么热衷的消遣吗？

刘：目前教本科生的《高等代数》。还带了 10 个博士生。除了教学研究，我对历史文化和数学史很感兴趣。

崔：谢谢您今天跟我们分享了这么多有趣的经历和美妙的数学。您有没有什么话是特别想对喜欢数学的年轻人说的？

刘：我觉得我没有资格来教化任何人，我已经谈了我自己的一些亲身感受。

附录：Ramanujan 写给 Hardy 的信中有 120 个公式，这里选取其中 15 个展示：

$$ \begin{array} { l } { 1 - \frac { 3 ! } { ( 1 ! 2 ! ) ^ { 3 } } x ^ { 2 } + \frac { 6 ! } { ( 2 ! 4 ! ) ^ { 3 } } x ^ { 4 } - \cdots } \\ { \quad = \left( 1 + \frac { x } { 1 ! ^ { 3 } } + \frac { x ^ { 2 } } { 2 ! ^ { 3 } } + \cdots \right) \left( 1 - \frac { x } { 1 ! ^ { 3 } } + \frac { x ^ { 2 } } { 2 ! ^ { 3 } } - \cdots \right) } \end{array}.\tag{1} $$ $$ 1 - 5 \left(\frac { 1} { 2 } \right) ^ { 3 } + 9 \left( \frac { 1 \cdot 3 } { 2 \cdot 4 } \right) ^ { 3 } - 13 \left( \frac { 1 \cdot 3 \cdot 5 } { 2 \cdot 4 \cdot 6 } \right) ^ { 3 } + \cdots = \frac { 2 } { \pi }.\tag{2} $$ $$ 1 + 9 \left(\frac { 1} { 4 } \right) ^ { 4 } + 17 \left( \frac { 1 \cdot 5 } { 4 \cdot 8 } \right) ^ { 4 } + 25 \left( \frac { 1 \cdot 5 \cdot 9 } { 4 \cdot 8 \cdot 12 } \right) ^ { 4 } + \cdots = \frac { 2 ^ { 3 / 2 } } { \sqrt { \pi } \Gamma ( 3 / 4 ) ^ { 2 } }.\tag{3} $$ $$ 1 - 5 \left(\frac { 1} { 2 } \right) ^ { 5 } + 9 \left( \frac { 1 \cdot 3 } { 2 \cdot 4 } \right) ^ { 5 } - 13 \left( \frac { 1 \cdot 3 \cdot 5 } { 2 \cdot 4 \cdot 6 } \right) ^ { 5 } + \cdots = \frac { 2 } { \Gamma ( 3 / 4 ) ^ { 4 } }.\tag{4} $$ $$ \begin{aligned} \int _ { 0 } ^ { \infty } & \frac { 1 + \left( \frac { x } { b + 1 } \right) ^ { 2 } } { 1 + \left( \frac { x } { a } \right) ^ { 2 } } \cdot \frac { 1 + \left( \frac { x } { b + 2 } \right) ^ { 2 } } { 1 + \left( \frac { x } { a + 1 } \right) ^ { 2 } } \cdots d x \\ & = \frac { \sqrt { \pi } } { 2 } \frac { \Gamma \left( a + \frac { 1 } { 2 } \right) \Gamma ( b + 1 ) \Gamma \left( b - a + \frac { 1 } { 2 } \right) } { \Gamma ( a ) \Gamma \left( b + \frac { 1 } { 2 } \right) \Gamma ( b - a + 1 ) } \end{aligned}.\tag{5} $$ $$ \int _ {0} ^ { \infty } \frac { d x } { \left( 1 + x ^ { 2 } \right) \left( 1 + r ^ { 2 } x ^ { 2 } \right) \left( 1 + r ^ { 4 } x ^ { 2 } \right) \ldots } = \frac { \pi } { 2 \left( 1 + r + r ^ { 3 } + r ^ { 6 } + r ^ { 10 } + \cdots \right) }.\tag{6} $$ $$ \begin{array} { l } { \text { If } \quad \alpha \beta = \pi ^ { 2 } , \text { then } } \\ { \alpha ^ { - 1 / 4 } \left( 1 + 4 \alpha \int _ { 0 } ^ { \infty } \frac { x e ^ { - \alpha x ^ { 2 } } } { e ^ { 2 \pi x } - 1 } d x \right) = \beta ^ { - 1 / 4 } \left( 1 + 4 \beta \int _ { 0 } ^ { \infty } \frac { x e ^ { - \beta x ^ { 2 } } } { e ^ { 2 \pi x } - 1 } d x \right) } \end{array}.\tag{7} $$ $$ \int _ {0} ^ { a } e ^ { - x ^ { 2 } } d x = \frac { 1 } { 2 } \sqrt { \pi } - \frac { e ^ { - a ^ { 2 } } } { 2 a + } \frac { 1 } { a + } \frac { 2 } { 2 a + } \frac { 3 } { a + } \frac { 3 } { 2 a + \cdots }.\tag{8} $$ $$ 4 \int _ {0} ^ { \infty } \frac { x e ^ { - x \sqrt { 5 } } } { \cosh x } d x = \frac { 1 } { 1 + } \frac { 1 ^ { 2 } } { 1 + } \frac { 1 ^ { 2 } } { 1 + } \frac { 2 ^ { 2 } } { 1 + } \frac { 2 ^ { 2 } } { 1 + } \frac { 3 ^ { 2 } } { 1 + } \frac { 3 ^ { 2 } } { 1 + \cdots }.\tag{9} $$ $$ \begin{aligned} { \text { If } u = \frac { x } { 1 + } \frac { x ^ { 5 } } { 1 + } \frac { x ^ { 10 } } { 1 + } \frac { x ^ { 10 } } { 1 + } \frac { x ^ { 15 } } { 1 + \cdots } , \quad v = \frac { x ^ { 1 / 5 } } { 1 + } \frac { x } { 1 + } \frac { x ^ { 2 } } { 1 + } \frac { x ^ { 3 } } { 1 + \cdots } } \\ { \text { then } v ^ { 5 } = u \frac { 1 - 2 u + 4 u ^ { 2 } - 3 u ^ { 3 } + u ^ { 4 } }{ 1 + 3 u + 4 u ^ { 2 } + 2 u ^ { 3 } + u ^ { 4 } } } \end{aligned}.\tag{10} $$ $$ \frac {1} { 1 + } \frac { e ^ { - 2 \pi } } { 1 + } \frac { e ^ { - 4 \pi } } { 1 + \cdots } = \left\{ \sqrt { \left( \frac { 5 + \sqrt { 5 } } { 2 } \right) } - \frac { \sqrt { 5 } + 1 } { 2 } \right\} e ^ { 2 \pi / 5 }.\tag{11} $$ $$ \frac {1} { 1 + } \frac { e ^ { - 2 \pi \sqrt { 5 } } } { 1 + } \frac { e ^ { - 4 \pi \sqrt { 5 } } } { 1 + \cdots } = \left[ \frac { \sqrt { 5 } } { 1 + \left( 5 ^ { 3 / 4 } \left( \frac { \sqrt { 5 } - 1 } { 2 } \right) ^ { 5 / 2 } - 1 \right) ^ { 1 / 5 } } - \frac { \sqrt { 5 } + 1 } { 2 } \right] e ^ { 2 \pi / \sqrt { 5 } }.\tag{12} $$ $$ \begin{array} { l } { \text { If } F ( k ) = 1 + \left( \frac { 1 } { 2 } \right) ^ { 2 } k + \left( \frac { 1 \cdot 3 } { 2 \cdot 4 } \right) ^ { 2 } k ^ { 2 } + \cdots \quad \text { and } } \\ { F ( 1 - k ) = \sqrt { 210 } F ( k ) , \quad \text { then } } \\ { k = ( \sqrt { 2 } - 1 ) ^ { 4 } ( 2 - \sqrt { 3 } ) ^ { 2 } ( \sqrt { 7 } - \sqrt { 6 } ) ^ { 4 } ( 8 - 3 \sqrt { 7 } ) ^ { 2 } ( \sqrt { 10 } - 3 ) ^ { 4 } } \\ { \times ( 4 - \sqrt { 15 } ) ^ { 4 } ( \sqrt { 15 } - \sqrt { 14 } ) ^ { 2 } ( 6 - \sqrt { 35 } ) ^ { 2 } } \end{array}.\tag{13} $$ The coefficient of $x ^ {n}$ in $( 1 - 2 x + 2 x ^ { 4 } - 2 x ^ { 9 } + \cdots ) ^ { - 1 }$ is the integer nearest to $$\frac {1} { 4 n } \left( \cosh \pi \sqrt { n } - \frac { \sinh \pi \sqrt { n } } { \pi \sqrt { n } } \right).\tag{14}$$ The number of numbers between $A$ and $x$ which are either squares or sums of two squares is $$K \int _ {A} ^ { x } \frac { d t } { \sqrt { \log t } } + \theta ( x ),\tag{15}$$ where $K = 0.764 \ldots$, and $\theta (x)$ is very small compared with the previous integral.

注释：

[1]Bruce C. Berndt. The Quarterly Reports of S. Ramanujan. The American Mathematical Monthly, Vol. 90, No. 8 (Oct., 1983), pp. 505-516

[2]"An Expansion Formula for $q$–Series and Applications"，The Ramanujan Journal, 6(2002), no. 4, 429-447.

[3]在有的文献中，为了简单起见，定义表达式的分母中出现的常数 ($q-1$) 会抹掉。

[4]On the $q$–partial differential equations and $q$–series，The legacy of Srinivasa Ramanujan, Ramanujan Math. Soc. Lect. Notes Ser. 20, Ramanujan Math. Soc., Mysore, (2013) 213-250.